Evaluation of the Performance Gains in Short-Term Water Consumption Forecasting by Feature Engineering via a Fuzzy Clustering Algorithm in the Context of Data Scarcity †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Resources
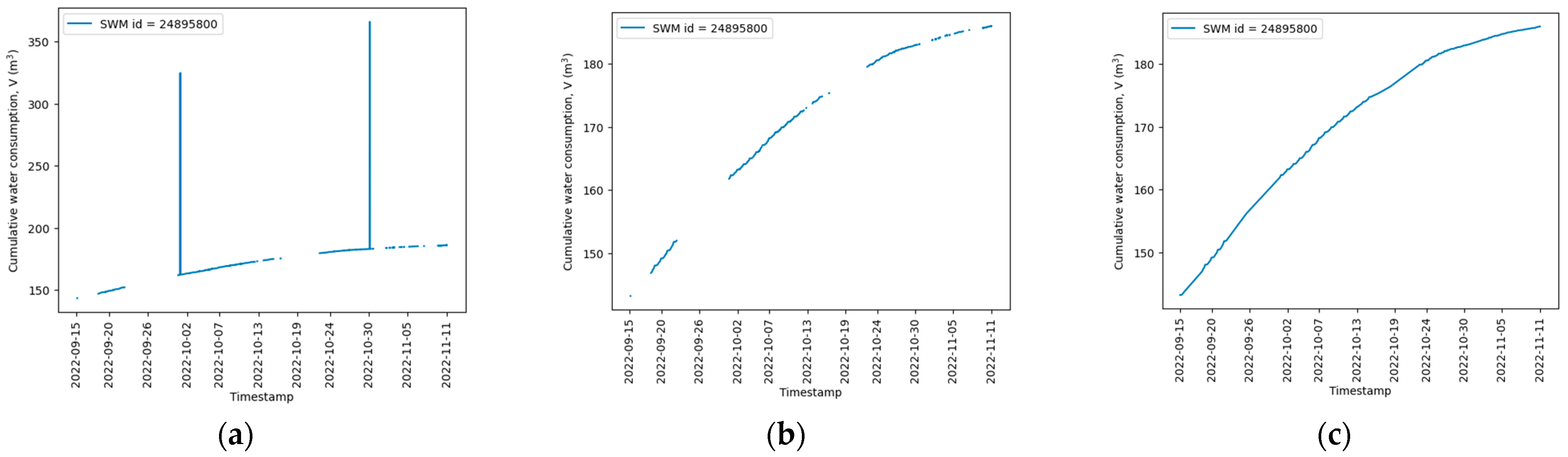
- Data filtration. The data during the testing period of the installations are discarded. These include data from between 1 August 2022 00:00 and 15 September 2022 00:00 and the readings of 18 SWMs. In addition, the data registered between 11 November 2022 00:10 and 11 November 2022 14:00 are discarded to maintain an exact number of days in the dataset. As an example, the collected measurements of an SWM with id = 24895800 are shown in Figure 1a;
- Time series resample. The 76 time series, one for each SWM, are resampled with a 10 min frequency. The process does not change the frequency of the time series but adds the missing timestamps. The missing values are filled with NaNs;
- Data imputation or removal. For each SWM, the ratio of NaNs to the sample size is computed. If the ratio is larger than 6%, then the SWM is discarded from the dataset. Otherwise, the data gaps are filled using linear interpolation, with the result for SWM 24895800 shown in Figure 1c. This step leads to the omission of 10 SWMs;
- Discharge computation. Each time series left is resampled with an hourly frequency, assigning the max. of every six measurements of 10 min duration to the start of every hourly period. Subsequently, the dataset is differentiated by one timestep. By doing so, the water consumption in terms of water discharge (m3/h) is obtained for each SWM;
- Aggregated water consumption computation. The AWC is computed as the sum of the remaining SWMs. The dataset contains 49 columns, 48 for each of the SWMs and one for the AWC. The row count is 1369 (timesteps). The dataset has a time index ranging between 15 September 2022 00:00 and 10 November 2022 23:00.
2.2. Machine Learning Pipeline
- The dataset is split into the train, validation and test subsets;
- The subsets are transformed to achieve stationarity using the train subset to compute the necessary transformation characteristics, thus avoiding data leakage;
- New features are engineered, aiming to reduce prediction errors;
- Data are reshaped in order to become consumable for the model;
- The model is built and trained using the train and validation subsets;
- The performance of the model is evaluated by comparing the ground truth (measurements) with the respective predictions that are produced using the test subset.
2.2.1. Data Split
2.2.2. Data Transformation
- The datasets are log transformed. The transformation reduces the distribution skewness while stabilizing variance over time;
- The log-transformed datasets are subsequently detrended using linear regression. The linear model is fitted (a = −0.000411, b = −0.444404) using the train subset;
- The datasets are standardized, meaning the subtraction of the average and the subsequent division by the standard deviation. The standard deviation and the mean are computed using the corresponding train subset.
2.2.3. Feature Engineering
- The SWMs are aggregated into groups using bins of 5 m3/h. The resulting groups have a larger correlation coefficient with the AWC;
- Seven new features are engineered using the statistical properties of the AWC. These include a comparison of the AWC with the previous daily mean, sum, max, 3rd and 1st quartile, as well as with the ramp during the last hour and the sum of the last 3 h.
- Initialization of the fuzzy partition, i.e., a matrix U(0), which contains the degree of membership μ in a predetermined number of clusters;
- Calculation of the corresponding vectors at the center of the clusters;
- Calculation of the Euclidean distance d between the data points (water consumption values) and the centers of the clusters;
- Calculation of the new membership degree μ and fuzzy partition matrix U(1);
- Convergence check, comparing pairwise each μ between U(0) and U(1). If the maximum absolute difference is greater than the predefined threshold ε = 0.001, steps (2) to (5) are repeated with new cluster centers; otherwise, the algorithm stops.
2.2.4. Deep Neural Networks Architecture
- A three-dimensional matrix is inserted into the encoder network. The results of the calculations of this network are: (a) the final memory content for the last timestep, which is called the context vector (CV), and (b) the outputs of the output layer, which are rejected. The CV is the input to the decoding network;
- In the decoding network, the CV from step (1) is entered for the first timestep and then iteratively continues the calculations using the network’s units.
- A CV is calculated for each ht of the encoding network. Without the mechanism, only the last timestep t to generate a single CV is considered;
- An alignment score is generated. The score is calculated based on the ht of the decoder (Luong attention mechanism) by a stacked neural network. This score may be interpreted as weights that give “attention” to the most “important” input data.
2.2.5. Tuning of the Hyperparameters
3. Results
3.1. Water Consumption Clustering
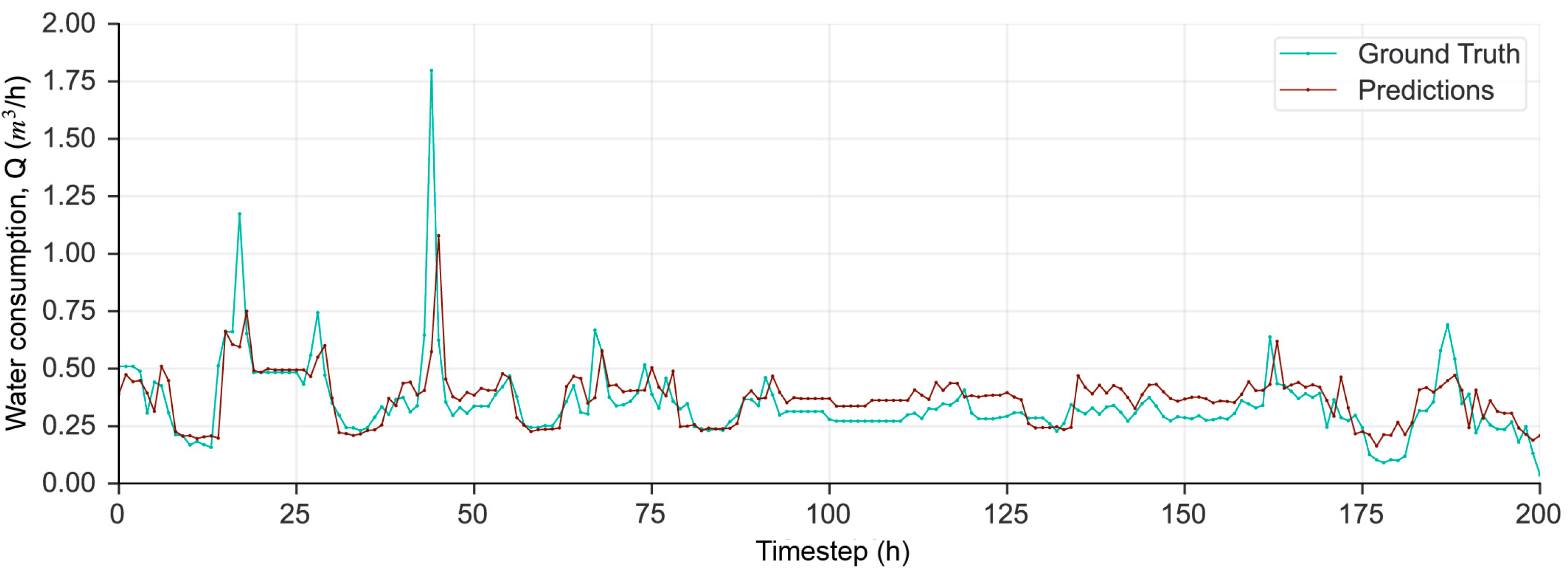
3.2. DNNs Performance
4. Discussion
5. Conclusions
Author Contributions
Funding

Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sarmas, E.; Spiliotis, E.; Marinakis, V.; Tzanes, G.; Kaldellis, J.K.; Doukas, H. ML-based energy management of water pumping systems for the application of peak shaving in small-scale islands. Sustain. Cities Soc. 2022, 82, 103873. [Google Scholar] [CrossRef]
- Kavya, M.; Mathew, A.; Shekar, P.R.; Sarwesh, P. Short term water demand forecast modelling using artificial intelligence for smart water management. Sustain. Cities Soc. 2023, 95, 104610. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis. In The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2008; pp. 192–194. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; Rostamizadeh, A.; Gonina, E.; Hardt, M.; Recht, B.; Talwalkar, A. A System for Massively Parallel Hyperparameter Tuning. arXiv 2018, arXiv:1810.05934. [Google Scholar]
- JDWarner/scikit-fuzzy: Scikit-Fuzzy Version 0.4.2. Available online: https://zenodo.org/record/3541386 (accessed on 1 June 2023).
- Tzanes, G.; Zafirakis, D.; Makropoulos, C.; Kaldellis, J.K.; Stamou, A.I. Energy vulnerability and the exercise of a data-driven analysis protocol: A comparative assessment on power generation aspects for the non-interconnected islands of Greece. Energy Policy 2023, 177, 113515. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to Sequence Learning with Neural Networks. arXiv 2014, arXiv:1409.3215. [Google Scholar]
- Luong, M.-T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-based Neural Machine Translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of ADAM and Beyond. In Proceedings of the 6th International Conference on Learning Representations, Vancouver Convention Center, Vancouver, BC, Canada, 30 April 2018–3 May 2018. [Google Scholar] [CrossRef]

| Nr. | Hyperparameter | Search Space |
|---|---|---|
| 1 | Units of the encoder and the decoder | Integer in [8, 768] |
| 2 | Encoder activation function | Choice from relu, sigmoid, softplus, softsign, tanh, selu, elu, exp and LeakyReLU |
| 3 | Decoder activation function | |
| 4 | Learning rate of the training algorithm | Choice from [0.0008, 0.01] |
| Nr. | Dataset | Model | MAE | RMSE |
|---|---|---|---|---|
| 1 | Without WCC | Seq2Seq-Attention-MAE | 0.118 | 0.164 |
| 2 | Seq2Seq-Attention-RMSE | 0.134 | 0.169 | |
| 3 | With WCC | Seq2Seq-Attention-MAE | 0.081 | 0.133 |
| 4 | Seq2Seq-Attention-RMSE | 0.098 | 0.145 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzanes, G.; Papapostolou, C.; Gymnopoulos, M.; Kaldellis, J.; Stamou, A. Evaluation of the Performance Gains in Short-Term Water Consumption Forecasting by Feature Engineering via a Fuzzy Clustering Algorithm in the Context of Data Scarcity. Environ. Sci. Proc. 2023, 26, 105. https://doi.org/10.3390/environsciproc2023026105
Tzanes G, Papapostolou C, Gymnopoulos M, Kaldellis J, Stamou A. Evaluation of the Performance Gains in Short-Term Water Consumption Forecasting by Feature Engineering via a Fuzzy Clustering Algorithm in the Context of Data Scarcity. Environmental Sciences Proceedings. 2023; 26(1):105. https://doi.org/10.3390/environsciproc2023026105
Chicago/Turabian StyleTzanes, Georgios, Christiana Papapostolou, Miltiadis Gymnopoulos, John Kaldellis, and Anastasios Stamou. 2023. "Evaluation of the Performance Gains in Short-Term Water Consumption Forecasting by Feature Engineering via a Fuzzy Clustering Algorithm in the Context of Data Scarcity" Environmental Sciences Proceedings 26, no. 1: 105. https://doi.org/10.3390/environsciproc2023026105
APA StyleTzanes, G., Papapostolou, C., Gymnopoulos, M., Kaldellis, J., & Stamou, A. (2023). Evaluation of the Performance Gains in Short-Term Water Consumption Forecasting by Feature Engineering via a Fuzzy Clustering Algorithm in the Context of Data Scarcity. Environmental Sciences Proceedings, 26(1), 105. https://doi.org/10.3390/environsciproc2023026105









