Hesitant Intuitionistic Fuzzy Approach in Optimal Irrigation Planning in India ^†

Abstract

The hesitant intuitionistic fuzzy optimization method optimizes multi-objective optimization problems under uncertainty and hesitation, and reflects the practical aspects of better decision-making. Hesitant intuitionistic fuzzy optimization (HIFO), a new optimization technique, has been suggested in the current study to find the best cropping pattern in the Kakrapar Right Bank Main Canal (KRBMC) command area of Ukai-Kakrapar Water Resources Project in India. The HIFO multi-objective fuzzy linear programming (HIFO MOFLP) result includes three objectives: maximization of net irrigation benefits (NIB), maximization of employment generation (EG), and minimization of cost of cultivation (CC), along with the appropriate constraints set. The performance of the aforesaid model is evaluated based on irrigation intensity, degree of acceptance (α^r), and degree of rejection (β^r) for inflows corresponding to 75% exceedance probability. The irrigation intensity from the study HIFO MOFLP model has been found to be 82.05%, while NIB, EG, and CC from the proposed model are 5572.31 million Rs, 14,287.27 thousand-man days, and 3429.99 million Rs, respectively. The proposed HIFO MOFLP model has been compared with the IFO MOFLP approach for the same command area and found to give improved results in the form of the irrigation intensity of the command area and objective function values. The current study demonstrates how hesitant fuzzy membership functions and non-membership functions can be applied to deal with uncertainty and hesitation in a real-world problem.

1. Introduction

Water resource planning and management has grown extremely complex as a result of competing and conflicting user needs. Furthermore, the estimation of irrigation demand, availability of labor, crop prices, and reservoir inflows are imprecise and uncertain in nature in water resource management and planning. In these situations, fuzzy optimization is the best suited to cope with uncertainty and impreciseness in the system. For the best irrigation planning for the Kakrapar right bank main canal (KRBMC) command area in India, Mirajkar and Patel [1] used multi-objective linear programming with a fuzzy decision set. They took into account three objectives and provided a compromise result with a degree of satisfaction (λ) of 0.503. Crisp linear programming was utilized by Mirajkar and Patel [2] to resolve three conflicting objectives: maximization of net irrigation benefit, employment creation, and minimization of cultivation costs. This problem was solved concurrently by finding a multi-objective fuzzy solution with maximum-minimum operators. Two-phase and fuzzy compromised techniques were used to improve the solution using maximum-minimum operator. These algorithms were validated for the KRBMC in the Ukai command area of India. Chen et al. [3] introduced a new fuzzy robust control method for linear parameter varying systems. Results from the proposed model revealed that the methodology has good efficiency and performance. The generalization of fuzzy sets by Atanassov [4] included the hesitation margin, which is equal to one minus the membership degree and the non-membership degree. The use of IFO in multi-objective linear programming was examined by Bharati and Singh [5], who also investigated the effects of linear and non-linear membership functions on optimization. Non-linear membership as well as non-membership functions outscored linear membership and non-membership functions in the IFO technique. Angelov [6] found that a membership degree, which is an objective function’s degree of acceptance, is not complimentary to non-membership or rejection. The study demonstrated that intuitionistic fuzzy optimization (IFO) solutions outperformed the traditional fuzzy and crisp optimization methods. Sahoo et al. [7] solved an MOFLP problem for the development and implementation of the land-water-crop system of the Mahanadi-Kathajodi Delta in Eastern India. A unique compromise ratio technique for multiple criterion decision-making in water resources management was introduced by Hashemi et al. [8] based on Atanassov’s intuitionistic fuzzy sets idea. Garai and Roy [9] developed the idea of the hesitation index for the optimization of a fictitious mathematical problem where the objective functions included maximization of the degree of acceptance, minimization of the degree of rejection, and hesitation. In order to assist policymakers in reducing water shortages, Li et al. [10] developed an intuitionistic fuzzy (IF) multi-objective non-linear programming (IFMONLP) method for allocating water for irrigation purposes in both dry and rainy circumstances. An ambiguous transportation issue was studied by Ebrahimnejad and Verdegay [11]. Intuitionistic fuzzy multi-objective geometric programming was proposed by Jafarian et al. [12] as a solution to multi-objective nonlinear programming issues. In order to establish the cropping pattern in the KRBMC command area of the Ukai-Kakrapar water resources project in India, Pawar et al. [13] adopted the IFO methodology as a new optimization method. Other uncertainty characteristics, such as the degree of acceptance, rejection, and hesitation, were also presented in addition to the best cropping pattern. To maximize net irrigation benefit, create jobs, and minimize cultivation costs, Pawar et al. [14] applied the IFO MOFLP model to optimize crop allocation in the Ukai-Kakrapar water resources project. For the multi-objective optimization issue, Bharati [15] provided a hesitant intuitionistic fuzzy approach, and an exemplary example demonstratingthe superiority of the suggested model.

2. Description of Study Area

One of the biggest multipurpose projects in India is the Ukai water resources project, which is situated on the Tapi River. The Kakrapar weir is situated 29 kilometers downstream of the Ukai Dam at latitude 21°22′ N and longitude 73°16′ E. The Kakrapar weir consists of two major canals for irrigation of the crops on both sides of the weir, namely, KRBMC and the Kakrapar left bank main canal (KLBMC), with 113,123 hectares and 145,335 hectares of culturable command areas, respectively. Pawar et al. [13] included the index map of the KRBMC inside the Ukai-Kakrapar project.

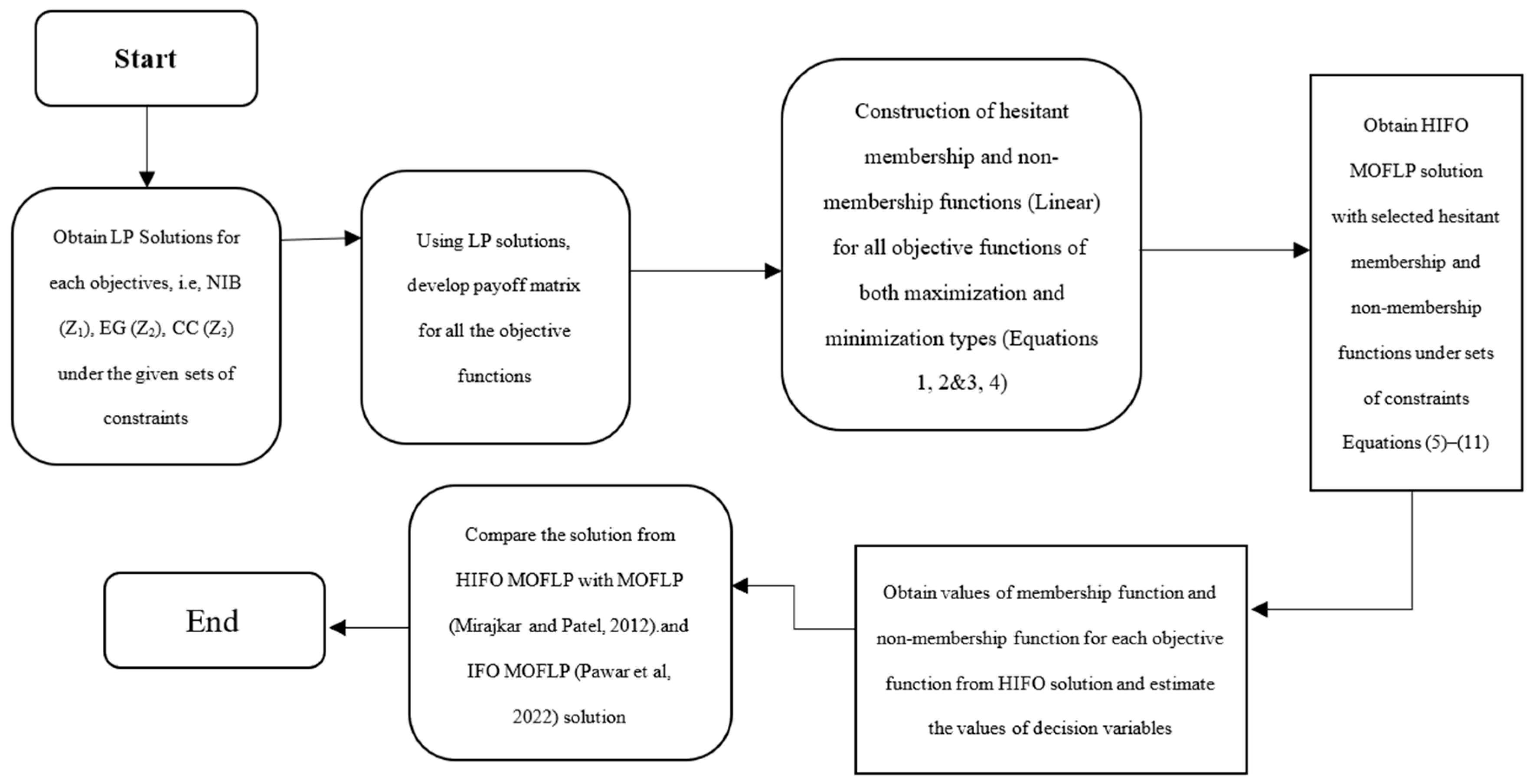
3. Methodology and Model Development

In this study, the best cropping pattern for the KRBMC command area is determined by maximizing net benefits, creating jobs, and minimizing cultivation costs under a specific set of constraints, namely, available water resources and land. Mirajkar and Patel [16] provided an outline of each objective and constraint, while Pawar et al. [13] described objective functions and constraints briefly.

3.1. Objective Functions and Constraints

In this study, the three objective functions, i.e., maximizing net irrigation benefits (Z₁), employment generation (Z₂), and minimizing cultivation costs (Z₃), are taken into account along with constraints on planting area, affinity, and water allocation. Section 4 describes the formulation of hesitant intuitionistic fuzzy optimization while using optimal solutions of individual objective functions.

3.2. Hesitant Intuitionistic Fuzzy Optimization (HIFO)

KRBMC has been taken into account in this study when using the HIFO approach. In Figure 1, a flow chart describing the details of HIFO implementation for the KRBMC area is shown. Using Equations (1) and (2), the hesitant membership and non-membership functions for the maximization type objective function are briefly described below.

$${\mu }_m^{E^r}(x)={\delta }^r\{\begin{array}{ccc}0& if& Z_m(x)\le L_m^{\mu }\\ \frac{Z_m(x)-L_m^{\mu }}{U_m^{\mu }-L_m^{\mu }}& if& L_m^{\mu }\le Z_m(x)\le U_m^{\mu }\\ 1& if& f_m(x)\ge U_m^{\mu }\end{array}$$

(1)

$$v_m^{E^r}(x)={\delta }^r\{\begin{array}{ccc}0& if& Z_m(x)\ge U_m^v\\ \frac{U_m^v-Z_m(x)}{U_m^v-L_m^v}& if& L_m^v\le Z_m(x)\le U_m^v\\ 1& if& Z_m(x)\le L_m^{\nu }\end{array}$$

(2)

Here, ${\mu }_m^r(x)$ is hesitant membership, ${\nu }_m^r(x)$ is hesitant membership and non-membership function for m^th objective function, $Z_m(X)$ is the value of the objective functions $U_m^{\mu }=\max (Z_m(X))$, $L_m^{\mu }=\min (Z_m(X))$, and $L_m^{\nu }=L_m^{\mu }$, $U_m^v=Ø\times U_m^{\mu },Ø\in \left[1,3\right]$. Here, m = 1, 2, and 3 are the numbers of objective functions, Ø is a hesitant parameter and δ^r is a multiplication factor with 0 ≤ δ^r ≤ 1wherein r = 1, 2, …,9.

(a)

The membership and non-membership functions were formed with Equations (3) and (4) in order to minimize the objective function.

$${\mu }_m^{E^r}(x)={\delta }^r\{\begin{array}{ccc}0& if& Z_m(x)\ge U_m^{\mu }\\ \frac{U_m^{\mu }-Z_m(x)}{U_m^{\mu }-L_m^{\mu }}& if& L_m^{\mu }\le Z_m(x)\le U_m^{\mu }\\ 1& if& Z_m(x)\ge L_m^{\mu }\end{array}$$

(3)

$$v_m^{E^r}(x)={\delta }^r\{\begin{array}{ccc}0& if& Z_m(x)\le L_m^v\\ \frac{Z_m(x)-L_m^v}{U_m^v-L_m^v}& if& L_m^v\le Z_m(x)\le U_m^v\\ 1& if& Z_m(x)\ge U_m^{\mu }\end{array}$$

(4)

Here, $U_m^{\mu }=\max (Z_m(X))$, $L_m^{\mu }=\min (Z_m(X))$, $L_m^{\nu }=L_m^{\mu }$, and $U_m^v=Ø\times U_m^{\mu },Ø\in \left[1,3\right]$. Here, m = 1,2, and 3 where 0 ≤ δ^r ≤ 1, r = 1, 2,…,9.

• (b) With the use of linear membership and non-membership excluding the hesitation index, the multi-objective fuzzy linear optimization problem (MOFLP) for objectives subject to constraints set can be described using Equations (5)–(11) (Bharti, [15]).

$$\mathrm{Maximize}{\displaystyle \sum ({\alpha }^r-{\beta }^r)}$$

(5)

$$\mathrm{Subject}\mathrm{to}{\alpha }^r\le {\mu }_m^{E^r}(x),$$

(6)

$${\beta }^r\ge v_m^{E^r}(x),$$

(7)

$${\alpha }^r+{\beta }^r\le 1,$$

(8)

$${\alpha }^r\ge {\beta }^r,$$

(9)

$${\beta }^r\ge 0,$$

(10)

$$g_j(x)\le b_j,x\ge 0,$$

(11)

$$m=1,2,\dots \dots p;j=1,2,\dots \dots q$$

Here, α^r signifies the degree of acceptance of objective functions, and β^r indicates the degree of rejection of objective functions under sets of constraints.

The objective functions, expressed using Equation (5), under the constraints set, were solved using the modified simplex method.

The application of the HIFO MOFLP approach for the KRBMC command area resulted in effective solutions for each of the objective functions, along with the crop areas for that command area. The three objectives considered are the maximization of NIB, maximization of EG, and minimization of CC. In addition to the suggested optimization technique, it provided better performance parameters, such as the degree of acceptance and the degree of rejection.

Table 1. Pay-off Matrix from LP solutions for three objective functions (Pawar et al. [13]).

Type of Objective Function	Objective Function	Net Benefit	Employment Generation	Cost of Cultivation
Maximum	Net benefit, in million Rs	5593.77 U	5559.32	1552.55 L
Maximum	Employment generation, in 1000 man-days	14,631.25	14,824.02 U	5499.49 L
Minimum	Cost of cultivation, in million Rs	3457.54 L	3454.37	1076.75 U

Note: ^U and ^L are the upper and lower values of an objective function.

implies the Pay-off Matrix for three objective functions derived from individual LP solutions.

4. Results and Discussion

For the selected study region, HIFO techniques from Bharati [15] have been applied. The performance of the HIFO MOFLP with MOFLP technique, as well as the ideal values for each of the objective functions and the appropriate crop pattern for the command area (Mirajkar and Patel [2]) and IFO MOFLP approach (Pawar et al. [13]) are described in the following paragraphs.

4.1. Sensitivity of δ^r on Hesitant Membership and Non-Membership Function

The values of δ^r, determining the membership and non-membership function, range from 0 to 1.0. The HIFO MOFLP for the KRBMC area has been optimized using Equations (5)–(11) for different values of δ^r and equivalent values of α^r and β^r were obtained. The values of α^r and β^r have been estimated as follows: α₁ = 0.97, α₂ = 0.98, α₃ = 0.99, α₄ = 0.05, α₅ = 0.03, α₆ = 0.02, α₇ = 0.01, α₈ = 0.01, α₉ = 0.01, β₁ = 0.01, β₂ = 0.01, β₃ = 0.01, β₄ = 0.95, β₅ = 0.97, β₆ = 0.98, β₇ = 0.00, β₈ = 0.00, and β₉ = 0.00. The decision maker must select the value of δ^r for its execution in the command area based on the level of certainty.

4.2. Optimal Cropping Pattern

Here, corresponding to Ø (hesitant parameter) = 1, the optimal values forδ¹, δ², δ³, δ⁴, δ⁵, δ⁶, δ⁷, δ⁸, and δ⁹ are 0.96, 0.98, 1, 0.96, 0.98, 1, 0.96, 0.98, and 1, respectively. The recommended modeling approach, suggested by Bharati [4] resulted in the values of NIB, EG, and CC as 5572.31 million Rs, 14,287.27 thousand-man days, and 3429.99 million Rs, respectively. The consequent values of an individual objective function with MOFLP and IFO MOFLP were 3585.05 million Rs, 10,189.21 thousand-man days, and 2260.13 million Rs, respectively.

It should be emphasized that HIFO MOFLP shows higher values of NIB, EG, and CC vis-à-vis MOFLP and IFO MOFLP approaches. Hence, the HIFO MOFLP solution can be used more reliably with respect to MOFLP and IFO MOFLP approaches.

The optimal values of the cropping pattern obtained from the HIFO MOFLP model, with Ø = 1, are included in

Table 2. Areas allocated to different crops (in ha) by IFO MOFLP, MOFLP, and HIFO MOFLP models.

Solutions Obtained from Various Models
		Crisp Linear Programming Individual Solutions *			IFO MOFLP *	MOFLP *	Hesitant Intuitionistic Algorithm
Crop No. (i)	Crops	Net benefit	Employment Generation	Cost of Cultivation	$\begin{array}{l}\alpha =0.503,\beta =0.282,\\ \pi =0.215,S_f=0.3\end{array}$	$\lambda$ = 0.503	α1 = 0.97, α2 = 0.98, α3 = 0.99, α4 = 0.05, α5 = 0.03, α6 = 0.02, α7 = 0.01, α8 = 0.01, α9 = 0.01, β1 = 0.01, β2 = 0.01, β3 = 0.01, β4 = 0.95, β5 = 0.97, β6 = 0.98, β7 = 0.00, β8 = 0.00, β9 = 0.00
		Cropareas allocated in ha
1	Paddy (k)	13,100	16,965	13,100	13,386.38	13,386.38	13,100
2	Juwar/Bajra (k)	11,310	11,310	8100	11,310	11,310	11,310
3	Vegetables (k)	1131	1131	690	1131	1131	1131
4	Wheat (r)	3654	3654	3654	16,965	16,965	3654
5	Vegetables (r)	1120	1120	1120	1120	1120	1120
6	Juwar/ Bajra (r)	10,091	10,091	10,091	10,091	10,091	10,091
7	Paddy (hw)	8145	8145	8145	8145	8145	8145
8	Groundnut (hw)	192	192	192	192	192	192
9	Cotton (ts)	860	860	860	860	860	860
10	Vegetables (ts)	5655	5655	1335	5655	5655	3077.996
11	Sugarcane (p)	38,337.21	37,350.34	4998	17,529.92	17,529.92	39,503
12	Banana (p)	633	633	633	633	633	633
	Total	94,228.21	97,106.34	52,918	87,018.3	87,018.3	97,106.34
	Irrigation Intensity %	83.30	85.84	46.78	76.92	76.92	82.05
Maximum	Net benefit, in million Rs	5593.77	5559.32	1552.55	3585.05	3585.05	5572.31
Maximum	Employment generation, in 1000 man-days	14,631.25	14,824.02	5499.49	10,189.21	10,189.21	14,287.27
Minimum	Cost of cultivation, in million Rs	3457.54	3454.37	1076.75	2260.13	2260.13	3429.99

Note: hw—hot weather; k—kharif; p—perennial; r—rabi; ts—two-season; *—taken from Pawar et al. [13].

, which can be applied in the KRBMC command area with a greater degree of certainty. Table 2 indicates areas allocated by the various optimization models used in the current study. The irrigation intensity for the same command area corresponding to the aforementioned condition has been found to be 82.05%.

Table 2 shows the optimal cropping pattern values from the HIFO MOFLP model for Ø = 1, which may be implemented in the KRBMC command region with a higher degree of reliability.

5. Conclusions

The hesitant intuitionistic fuzzy optimization with multi-objective fuzzy linear programming (HIFO MOFLP) has been implemented for the KRBMC of Ukai-Kakrapar irrigation project. The HIFO approach, given by Bharati [15], has been used for the selected study area. Finally, the outcomes of HIFO MOFLP were compared with those of MOFLP and IFO MOFLP for the same research area, same sets of constraints, and objective functions. The primary conclusions from the current research are as follows:

(a)

The HIFO MOFLP model, recommended by Bharati [15], has been applied over KRBMC with compromised optimal values of NIB, EG, and CC as 5572.31 million Rs., 14,287.27 thousand man-days, and 3429.99 million Rs, respectively.

(b)

The optimal cropping pattern, determined by HIFO MOFLP, is shown in Table 2 with an irrigation intensity of 82.05%.

(c)

The results obtained from the proposed model give improved results in terms of irrigation intensity and objective function values as compared with Mirajkar and Patel [2] and Pawar et al. [13] for the same study area and objective functions.

(d)

The proposed methodology can be applied to the whole Ukai-Kakrapar command area while giving due consideration to more objectives and corresponding constraints such as inflows, outflows of the reservoir, evaporation losses from the reservoir, etc., which are uncertain in nature. The hesitant intuitionistic fuzzy optimization approach can be discovered further when membership function and non-membership functions are non-linear in nature.