Comparison of the Performance of CMIP5 and CMIP6 in the Prediction of Rainfall Trends, Case Study Quebec City †
Abstract
:1. Introduction
2. Methods and Materials
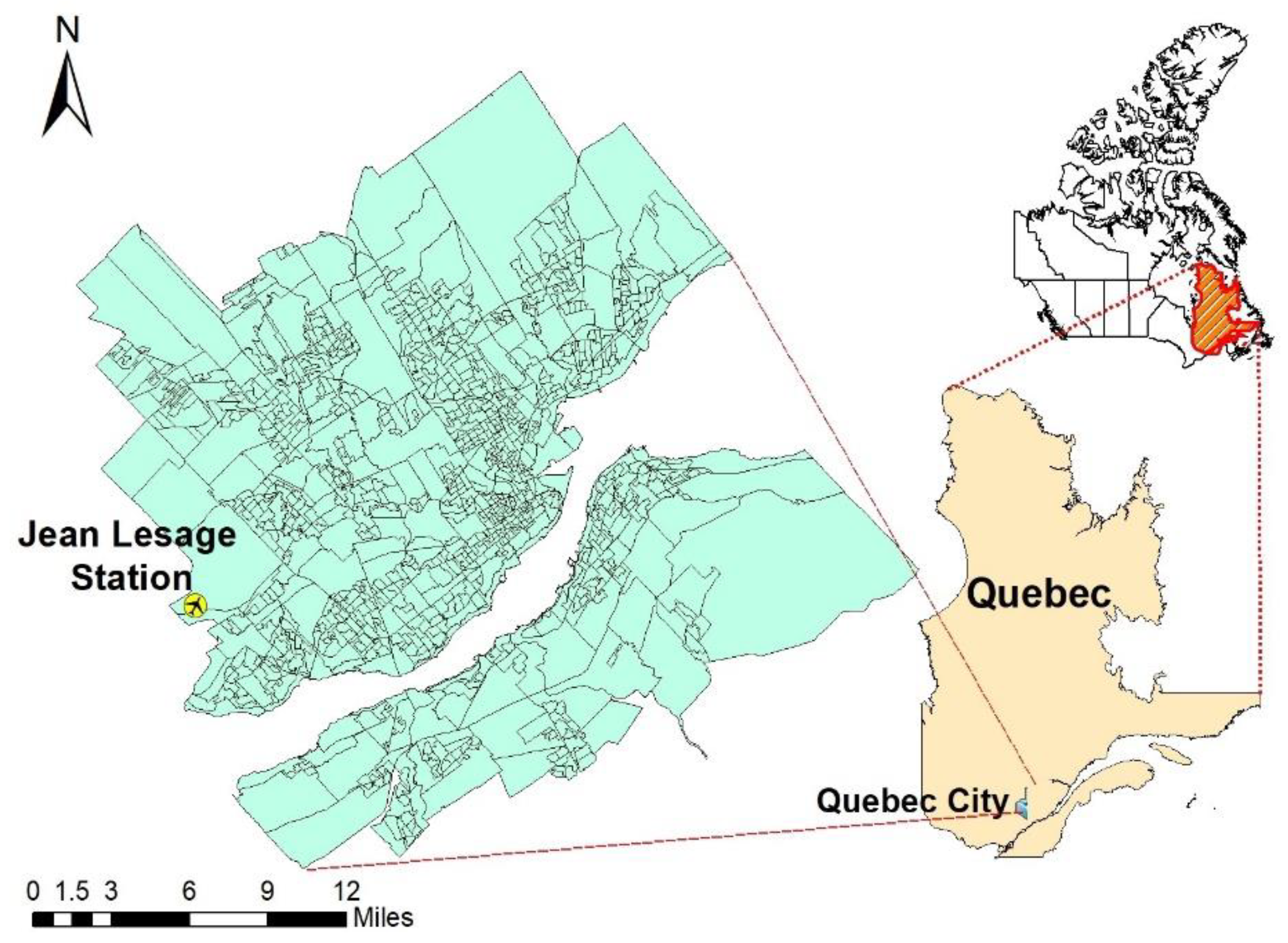
2.1. Data and Models
2.2. General Circulation Models
2.3. Mann–Kendall Trend Analysis
2.4. Evaluation of Performance
3. Results
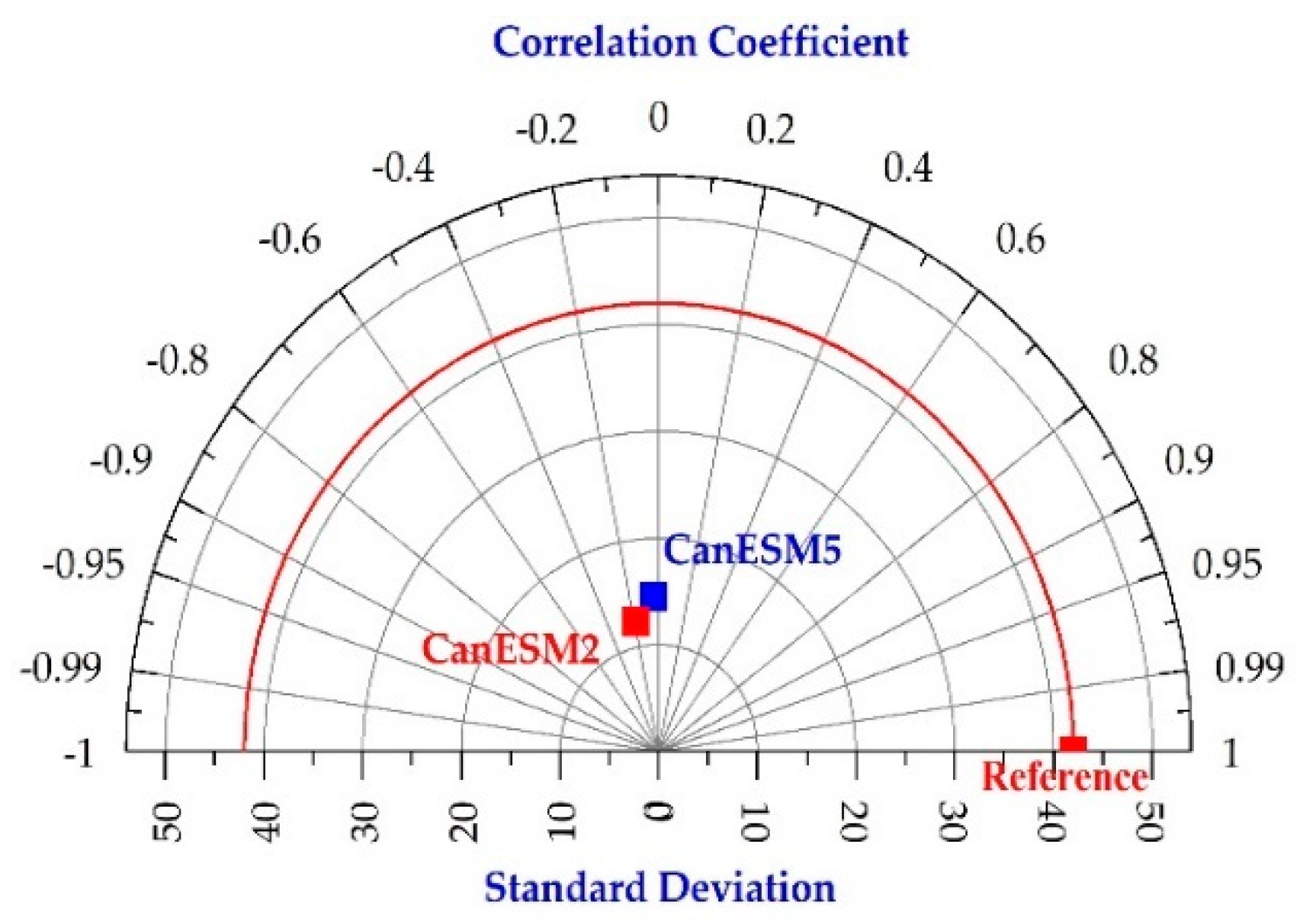
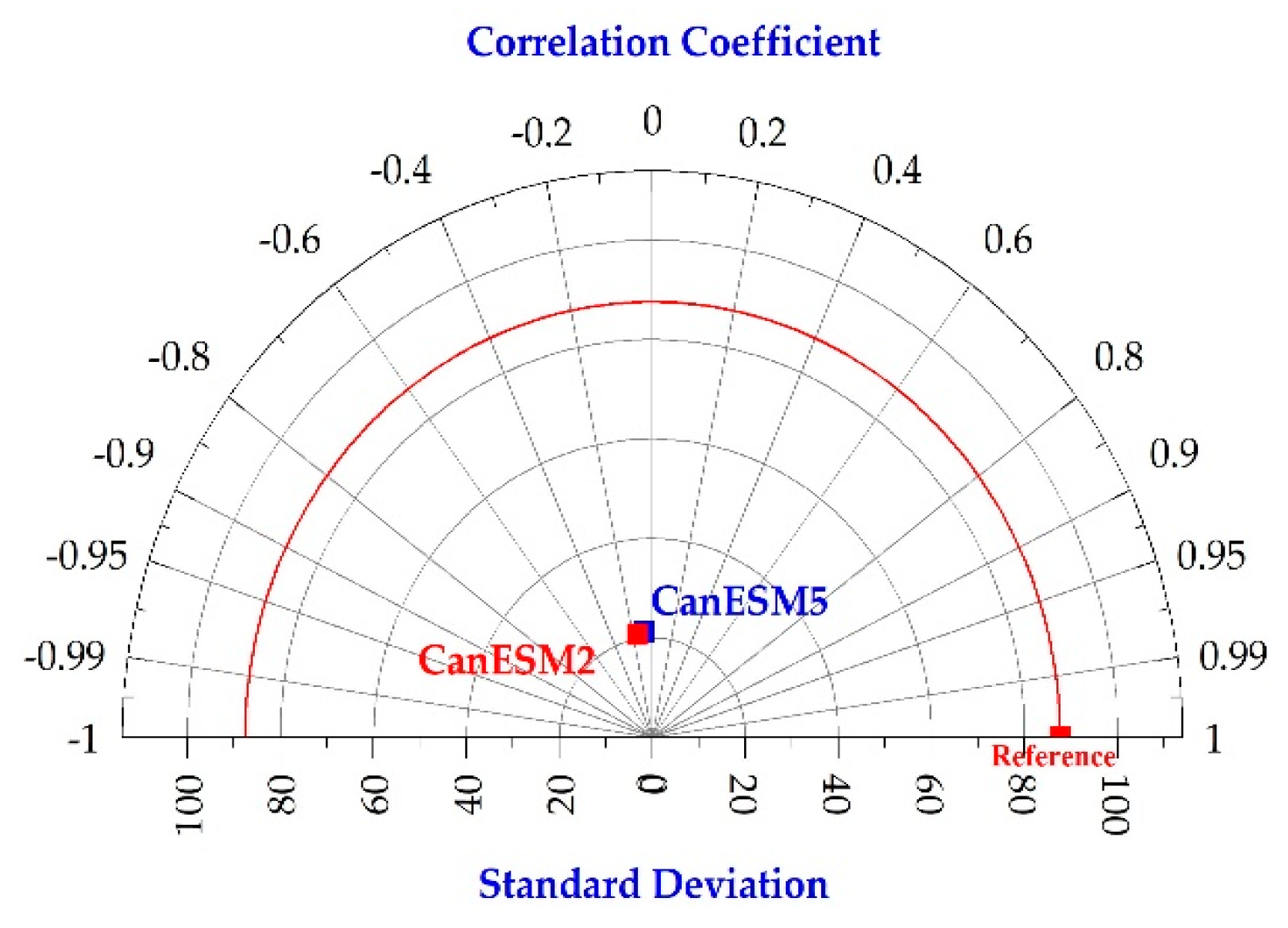
3.1. Evaluation the Performance of the Models
3.2. Precipitation Future Trend
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Salimi, A.H.; Masoompour Samakosh, J.; Sharifi, E.; Hassanvand, M.R.; Noori, A.; von Rautenkranz, H. Optimized artificial neural networks-based methods for statistical downscaling of gridded precipitation data. Water 2019, 11, 1653. [Google Scholar] [CrossRef]
- IPCC. Summary for Policy Markers Climate Change: The Physical Science Basis. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007; p. 881. [Google Scholar]
- Sobie, S.R.; Zwiers, F.W.; Curry, C.L. Climate Model Projections for Canada: A Comparison of CMIP5 and CMIP6. Atmos. Ocean. 2021, 59, 269–284. [Google Scholar] [CrossRef]
- Lovejoy, S. The Future of Climate Modelling: Weather Details, Macro weather Stochastics—Or both? Meteorology 2022, 1, 414–449. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H. A comprehensive comparison of the fifth and sixth phases of the coupled model intercomparison project based on the Canadian earth system models in spatio-temporal variability of long-term flood susceptibility using remote sensing and flood frequency analysis. J. Hydrol. 2023, 617, 128851. [Google Scholar]
- Martel, J.L.; Brissette, F.; Troin, M.; Arsenault, R.; Chen, J.; Su, T.; Lucas-Picher, P. CMIP5 and CMIP6 model projection comparison for hydrological impacts over North America. Geophys. Res. Lett. 2022, 49, e2022GL098364. [Google Scholar] [CrossRef]
- Miara, A.; Macknick, J.E.; Vörösmarty, C.J.; Tidwell, V.C.; Newmark, R.; Fekete, B. Climate and water resource change impacts and adaptation potential for US power supply. Nat. Clim. Chang. 2017, 7, 793–798. [Google Scholar] [CrossRef]
- Eyring, V.; Gleckler, P.J.; Heinze, C.; Stouffer, R.J.; Taylor, K.E.; Balaji, V.; Guilyardi, E.; Joussaume, S.; Kindermann, S.; Lawrence, B.N.; et al. Towards improved and more routine Earth system model evaluation in CMIP. Earth Syst. Dyn. 2016, 7, 813–830. [Google Scholar]
- Extracted from the Environment and Climate Change Canada Historical Climate Data. Available online: https://climate.weather.gc.ca/index_e.html (accessed on 4 December 2022).
- Hussain, M.; Mahmud, I. pyMannKendall: A python package for non-parametric Mann Kendall family of trend tests. J. Open Source Softw. 2019, 4, 1556. [Google Scholar] [CrossRef]
- Hidalgo, H.G.; Alfaro, E.J. Skill of CMIP5 Climate Models in Reproducing 20th Century Basic Climate Features in Central America. Int. J. Climatol. 2014, 35, 3397–3421. [Google Scholar] [CrossRef]
- Rupp, D.E.; Abatzoglou, J.T.; Hegewisch, K.; Mote, M. Evaluation of CMIP5 20th century climate simulations for the Pacific Northwest USA. J. Geophys. Res. Atmos. 2013, 118, 10884–10906. [Google Scholar] [CrossRef]
- Mehran, A.; AghaKouchak, A.; Phillips, T.J. Evaluation of CMIP5 continental precipitation simulations relative to satellite-based gauge-adjusted observations. J. Geophys. Res. 2014, 119, 1695–1707. [Google Scholar] [CrossRef]
| Model | CMIP | Scenario | Resolution |
|---|---|---|---|
| CanESM2 | 5 | RCP 2.6, 4.5, 8.5 | |
| CanESM5 | 6 | SSP 2.6, 4.5, 8.5 |
| Model | Scale | R | NRMSE | RMSRE | Bias | Slope |
|---|---|---|---|---|---|---|
| CanESM2 | Monthly | 0.43 | 0.40 | 0.36 | −85.6 | −0.30 |
| CanESM5 | 0.48 | 0.54 | 0.30 | −58.7 | 0.20 | |
| CanESM2 | Seasonal | 0.65 | 1.51 | 0.96 | −11.8 | 0.50 |
| CanESM5 | 0.75 | 1.08 | 0.67 | −10.3 | 0.13 |
| Time Series | 4.5 Test Z | 8.5 Test Z | Time Series | 4.5 Test Z | 8.5 Test Z |
|---|---|---|---|---|---|
| Jan. | 1.48 | 0.04 | Jul. | −1.78 | 1.89 |
| Feb. | −0.30 | 0.25 | Aug. | −0.36 | 1.53 |
| Mar. | 0.16 | −0.71 | Sep. | 1.30 | 0.14 |
| Apr. | −0.43 | −0.79 | Oct. | 2.02 | 2.86 |
| May. | −1.07 | 1.46 | Nov. | 1.30 | 0.18 |
| Jun. | −0.46 | −0.09 | Dec. | 1.48 | 1.71 |
| Spring | 0.71 | −0.18 | |||
| Summer | −1.25 | 0.39 | Annual | 0.00 | 2.82 |
| Fall | −1.32 | 2.32 | |||
| Winter | 1.78 | 2.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salimi, A.; Ghobrial, T.; Bonakdari, H. Comparison of the Performance of CMIP5 and CMIP6 in the Prediction of Rainfall Trends, Case Study Quebec City. Environ. Sci. Proc. 2023, 25, 42. https://doi.org/10.3390/ECWS-7-14243
Salimi A, Ghobrial T, Bonakdari H. Comparison of the Performance of CMIP5 and CMIP6 in the Prediction of Rainfall Trends, Case Study Quebec City. Environmental Sciences Proceedings. 2023; 25(1):42. https://doi.org/10.3390/ECWS-7-14243
Chicago/Turabian StyleSalimi, Amirhossein, Tadros Ghobrial, and Hossein Bonakdari. 2023. "Comparison of the Performance of CMIP5 and CMIP6 in the Prediction of Rainfall Trends, Case Study Quebec City" Environmental Sciences Proceedings 25, no. 1: 42. https://doi.org/10.3390/ECWS-7-14243
APA StyleSalimi, A., Ghobrial, T., & Bonakdari, H. (2023). Comparison of the Performance of CMIP5 and CMIP6 in the Prediction of Rainfall Trends, Case Study Quebec City. Environmental Sciences Proceedings, 25(1), 42. https://doi.org/10.3390/ECWS-7-14243







