Abstract
Effective mixing between contaminated water and nanoparticles is of great importance in various purification applications of microfluidics, especially when heavy metals are involved. Electromagnetic and shear mixing is combined here to explore optimization mixing strategies. A contaminated water stream is confined between two fresh-water streams loaded with nanoparticles and their mixing is studied numerically. The magnetic mixing is superimposed here with a time-modulated gradient external magnetic field. Results show that as velocity ratio increases, mixing between the heavy metals and nanoparticles grows more efficient, mainly due to increased shear, however, magnetic field action is catalytic to homogenise the mixture as water streams move away from the inlets. The present findings may shorten the path to purifying water and reduce its shortage.
1. Introduction
Modern water flow simulations explore novel mechanisms occurring at the nanoscale for water purification [1]. A significant category of water pollutants are heavy metals, i.e., those elements with density exceeding 5 g/cm3 [2]. Table 1 lists various metal ions of relevance in environmental and health contexts [3]. The combined properties of heavy metals i.e., non-biodegradable, unmetabolized or decomposed and their ability of accumulation in environmental systems [4] make them extremely dangerous for human health. In recent decades, progress has been made in the field of nanotechnology and extended knowledge has been acquired for synthesis, characterization and possible applications of nanoparticles [5]. The use of nanoparticles permits the increase in available surface of contact in the reaction with heavy metals leading to a reduced amount of biosorbent dose and retention time [6]. In case of biosorption, the heavy metal ions are adsorbed on the surface or active site of biosorbents [7], hence a possible solution for removing heavy metals from contaminated water is mixing with magnetic nanoparticles under chemical reactions. This solution enhanced knowledge of the specific properties of magnetic nanoparticles such as their large surface area. but also the considerable number of surface atoms, which leads to an increased amount of active sites [8]. The main purpose of this numerical study was to achieve the optimum mixing between streams of nanoparticles and contaminated water, where the heavy metal captured by nanoparticles through catalytic reactions. These catalytic reactions are found to depend on the size of nanoparticles and size distribution, but also on the nanoparticle environment such as pH and temperature [9]. Higher catalytic efficiency was observed for low-volume nanoparticles rather than high-volume nanoparticles [10] and for monodisperse size distribution, which is usually effective with surfactants as colloidal stabilizers; these surfactants also prevent agglomeration of the nanoparticles [5]. Several studies investigated synthesis of the nanoparticles and adsorption properties of Fe3O4 magnetic nanoparticles for removal heavy metal ions, among them Chang and Chen [11] which found that adsorption equilibrium time was 1 min for monodisperse Fe3O4 magnetic nanoparticles with a mean diameter size of 13.5 nm. Relevant research, using magnetic graphene oxide (MGO), succeeds adsorption capacity of MGO for heavy metal ions equal to 87.51% for adsorption equilibrium time within 30 min [12]. Another encouraging observation from recent research is ion drifting in microchannel under external factors such as electric field [13]. Moreover, interesting results can be found about factors of effective mixing, driving and collecting magnetic nanoparticles. The collecting efficiency depends on the Reynolds number, nanoparticle diameter and strength of the magnetic field [14,15]. The mixing efficiency depends on the velocities’ ratio but is not affected by incoming angles of flow streams [16]. The most important parameter of driving magnetic nanoparticles was found to be the external magnetic field magnitude [17].

Table 1.
Heavy Metal toxicity [3].
In the present study, a heavy-metal-contaminated water stream and two freshwater streams loaded with nanoparticles were inserted in a microfluidic duct with variable inlet velocity ratios. Excepting slow shearing, the mixing of heavy metals with nanoparticles is due to the magnetic field where its permanent and gradient components are temporarily variated. Numerical simulations are performed for the study of inflow and magnetic frequency effect on the particle distribution in the duct. The methodology for water flow and particles motion simulation is described in Section 2. The results of the mixing performance are discussed in Section 3, giving emphasis to the influence of inlet velocity ratios and magnetic frequency. Finally, the most important conclusions are summarized in Section 4.
2. Materials and Methods
The slow water flow in the micromixer duct is expected to be laminar and steady-state. The squared cross-section micromixer is of L = 5 × 10−4 m length and equal height and has a width of W = H = 10−4 m. The three water streams enter micromixer from different inlets, are mixed and leave the domain from the common outlet, as shown in Figure 1. The incompressible Navier–Stokes equations are solved in the Eulerian frame, for the pressure and velocity u, together with a model for the discrete motion of particles in a Lagrangian frame. Due to microfluidic duct size, nanoscale effects such as wall interference on fluid properties and transport properties [18] are suppressed. Governing equations of the fluid phase are given by [17]:
where t is time and v the kinematic viscosity of the water. The motion equations of each single particle in the discrete frame are based on the Newton law and may read as follows:
where the index i stands for the ith -particle with diameter di, ui, and ωi are its transversal and rotational velocities, respectively, and mi is its mass. The mass moment of inertia matrix is Ii and the terms ∂ui/∂t and ∂ωi/∂t correspond to the linear and angular accelerations, respectively. Fmag,i is the magnetic force, while Fnc,i and Ftc,i are the normal and tangential contact forces, respectively. Fdrag,i stands for the hydrodynamic drag force, Fgrav,i is the total force due to buoyancy. Tmag,i is the magnetic torque, while Mdrag,i and Mcon,i are the drag and contact moments, respectively. An external magnetic field consists of a time-dependent part: By = B0sin (2πft), where B0 is its magnitude, f its frequency and by a magnetic gradient, Gy, which are aligned in the y direction and act together. Because the magnetic field is mainly in the y-direction, Bx, Bz can be neglected and the corresponding magnetic actuation force is mostly along the y-direction [15].
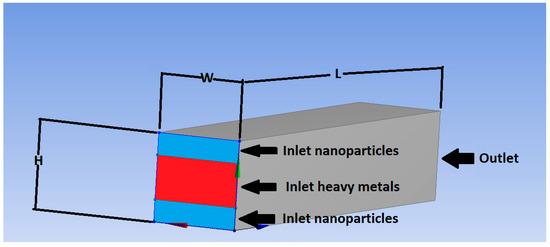
Figure 1.
Micromixer geometry and nanoparticles-heavy metals inlets and outlet flow directions.
The OpenFoam platform is used for the calculation of the flow field and the uncoupled equations of particle motion [19,20]. The simulation process reads as follows: initially, the fluid flow is found using the incompressible Navier–Stokes equations and the pressure correction method. Upon finding the flow field, pressure and velocity, the motion of particles is evaluated by the Lagrangian method. The equations are evolved in time by Euler’s time marching method. A computational grid composed by 40,000 (hexaedra) cells is used here, which is adequate for the low Reynolds number of the flow, whose maximum value is of the order Re = U0*H/v ≈ 2 × 10−2, based on the height of the duct and mean velocity . Details of the numerical models, force and moment terms used on equations may be found in [17,21]. Paramagnetic nanoparticles that are affected by the external magnetic field are used for mixing with heavy metals. It should be noticed that particles can oscillate under the action of the magnetic force when an alternating uniform magnetic field is applied [22].
3. Results
A series of simulations are performed with different velocity ratios of the contaminated water (Vc) and the nanoparticle solution (Vp) streams for various frequencies of the permanent and gradient magnetic field for optimum mixing. Simulation parameters as well as the boundary conditions are tabulated in Table 2. The adsorption capacity is strongly related to metal ion concentration [23]. In the relevant research field, the initial concentration ratio Cnanoparticles/Cheavy_metals varies. Relative results showed that fast (0.5 min) mixing is established for initial concentration ratio up to 2.5 [24].

Table 2.
Simulation parameters.
Results and statistics from the water-particle mixing process are recorded at the half-exit part of the duct for x ≥ L/2, where shear mixing is mostly diminished and nanoparticles are mixed with the heavy metals due to magnetic field. Flow streamlines for the inlet velocity ratios of Vp/Vc = 1, 5, 10 and 20 under a frequency of 5 Hz are depicted in Figure 2 (left). In addition, particle snapshots in the micromixer for the same velocity ratios for a magnetic field frequency of 5 Hz are presented in Figure 2 (right). It is found that, as inlet velocity ratio increases, nanoparticles more easily approach the central part of the duct, and thus they are more effectively mixed with the heavy metal particles. For an inlet ratio of Vp/Vc = 1, nanoparticle and heavy metal streams are nearly parallel to each other and no mixing at all is observed, as is depicted in Figure 2a. For the highest inlet velocity ratio of Vp/Vc = 20, nanoparticles and heavy metal particles streams are more
effectively mixed, as is depicted in Figure 2d. Similar images were observed for the lower frequencies for the corresponding velocity ratios. This phenomenon is due to the increased shearing observed locally at the inlet, however, as can be seen, it also stops quite soon after the streams enter the duct. Thus, particles cannot efficient transferred at the central part of the duct, and in order to optimize mixing, we exploit the magnetic mixing using an appropriate external
magnet field.
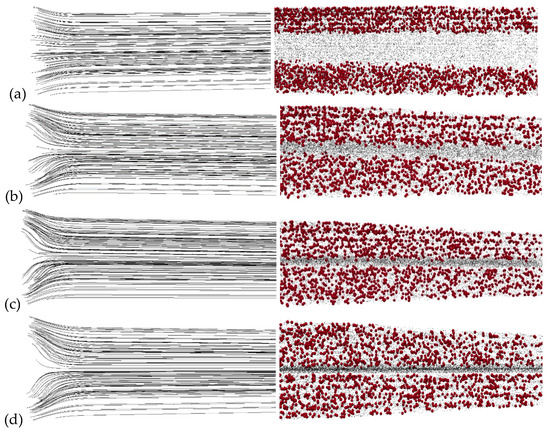
Figure 2.
Streamlines (left) for length x ≤ L/2 and snapshots of the nanoparticles (red color) and heavy metals (black color) positions (right) for x ≥ L/2 under B0 = 10 T, G = 10 T/m, f = 5 Hz and (a) Vp/Vc = 1, (b) Vp/Vc = 5, (c) Vp/Vc = 10 (d) Vp/Vc = 20.
The concentration of nanoparticles and heavy metals in the last half of the duct are shown in Figure 3a–d for velocity ratios, Vp/Vc = 1, 5, 10 and 20, respectively, under frequencies of the magnetic field with values 5, 1 and 0.1 Hz. The height of the duct H is divided into 10 equal layers and in these layers the concentration of nanoparticles and heavy metals is calculated.
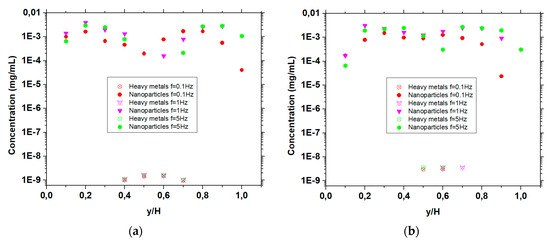
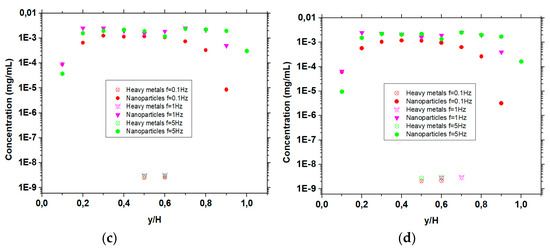
Figure 3.
Concentration of nanoparticles and heavy metals near the duct exit for under B0 = 10 T, G = 10 T/m and various frequencies (f = 5 Hz, f = 1 Hz, f = 0.1 Hz), (a) , (b) , (c) , and (d) .
In the case of Vp/Vc = 1 (Figure 3a), no mixing is observed under frequencies of 1 and 5 Hz, since all the nanoparticles are concentrated near the edges of the micromixer, while the heavy metals are in the centre of the duct, as seen in Figure 2a. Using a frequency of 0.1 Hz, a better distribution of nanoparticles is observed, however, we do not have effective mixing across the duct. In the case of Vp/Vc = 5 (Figure 3b), under frequency of 5 Hz, nanoparticles are more spread and also exist in regions where heavy metals exist. As the frequency decreases (1 Hz), nanoparticles and heavy metal particles are located at the same layers of the duct. A further decrease in the frequency (0.1 Hz) results in a very small area where nanoparticles are not mixed with the heavy metal particles. Increasing the ratio of stream velocities further (Vp/Vc = 10) (Figure 3c) results in a mixing of the two streams, as seen in Figure 2c, for frequencies equal to 5 Hz. Similar results are observed under frequencies of 1 and 0.1 Hz. As the velocity ratio between the streams of nanoparticles and heavy metals is further increased (Vp/Vc = 20), a more effective mixing is observed (Figure 3d), under a frequency of 5 Hz, as seen in Figure 2d. The nanoparticles are located nearly in all areas across the height of the duct, and thus we can reasonably expect that they can absorb the heavy metals under frequencies of magnetic field with values 5, 1 and 0.1 Hz. In addition, an almost parabolic profile of concentration is attained, due to the decrease in frequency and increase in velocity ratio (as we can see in Figure 3a–d).
4. Conclusions
The effect of frequency of the magnetic field under different velocity ratios between the streams of nanoparticles and heavy metal ions for an effective mixing is studied in the present work. It is found that for small velocity ratios, Vp/Vc, the mixing process efficiency is very low. As the velocity ratio increases, the mixing efficiency is improved under the action of the magnetic field. Under Vp/Vc = 5, mixing is observed for all frequencies, while as the velocity ratio further increases a more effective mixing between the heavy metal ions and the nanoparticles is achieved. Besides this, as the frequency of the magnetic field decreases, it is observed that for even a small velocity ratio a better distribution in the duct is attained. Further investigation of this particular geometry seems encouraging, especially the initial concentration, which is major factor for the absorption mechanism, but also parameters such as external magnetic field and contact time should be thoroughly investigated.
Author Contributions
Conceptualization, E.K.; methodology, EK.; software, C.L.; validation, C.L. and I.S.; formal analysis, C.L.; investigation, E.K.; resources, T.K.; data curation, T.K.; writing—original draft preparation, C.L.; writing—review and editing, I.S.; visualization, E.K.; supervision, T.K.; project administration, T.K. All authors have read and agree to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Authors are grateful to Greek Research & Technology Network (GRNET) for the computational time granted in the National HPC facility ARIS.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sofos, F.; Karakasidis, T.E.; Spetsiotis, D. Molecular dynamics simulations of ion separation in nano-channel water flows using an electric field. Mol. Simul. 2019, 45, 1395–1402. [Google Scholar] [CrossRef]
- Barakat, M.A. New trends in removing heavy metals from industrial wastewater. Arab. J. Chem. 2011, 4, 361–377. [Google Scholar] [CrossRef]
- Babel, S.; Kurniawan, T.A. Low-Cost adsorbents for heavy metals uptake from contaminated water: A review. J. Hazard. Mater. 2003, 97, 219–243. [Google Scholar] [CrossRef]
- Karvelas, E.; Liosis, C.; Karakasidis, T.; Sarris, I. Mixing of particles in micromixers under different angles and velocities of the incoming water. Proceedings 2018, 2, 577. [Google Scholar] [CrossRef]
- Bönnemann, H.; Nagabhushana, K.S.; Richards, R.M. Colloidal nanoparticles stabilized by surfactants or organo-aluminum derivatives: Preparation and use as catalyst precursors. In Nanoparticles and Catalysis; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar] [CrossRef]
- Beni, A.A.; Esmaeili, A. Biosorption, an efficient method for removing heavy metals from industrial effluents: A review. Environ. Technol. Innov. 2020, 17, 100503. [Google Scholar] [CrossRef]
- Podstawczyk, D.; Witek-Krowiak, A.; Dawiec, A.; Bhatnagar, A. Biosorption of copper(II) ions by flax meal: empirical modeling and process optimization by response surface methodology (RSM) and artificial neural network (ANN) simulation. Ecol. Eng. 2015, 83, 364–379. [Google Scholar] [CrossRef]
- Bronstein, L.M.; Matveeva, V.G.; Sulman, E.M. Nanoparticulate catalysts based on nanostructured polymers. In NNanoparticles and Catalysis; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar] [CrossRef]
- Somorjai, G.A.; Contreras, A.M.; Montano, M.; Rioux, R.M. Clusters, surfaces, and catalysis. Procceedings 2006, 103, 10577–10583. [Google Scholar] [CrossRef] [PubMed]
- Astruc, D. Transitio-Metal nanoparticles in catalysis : From historical background to the stat-of-the art. In Nanoparticles and Catalysis; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Chang, Y.-C.; Chen, D.-H. Preparation and adsorption properties of monodisperse chitosan-bound fe3o4 magnetic nanoparticles for removal of Cu(II) Ions. J. Colloid Interface Sci. 2005, 283, 446–451. [Google Scholar] [CrossRef] [PubMed]
- Ain, Q.-U.; Farooq, M.U.; Jalees, M.I. Application of magnetic graphene oxide for water purification: heavy metals removal and disinfection. J. Water Process Eng. 2020, 33, 101044. [Google Scholar] [CrossRef]
- Bartzis, V.; Sarris, I.E. A Theoretical model for salt ion drift due to electric field suitable to seawater desalination. Desalination 2020, 473, 114163. [Google Scholar] [CrossRef]
- Asghari, E.; Moosavi, A.; Hannani, S.K. Simulation of water purification using magnetically ultra-responsive micro- and nanoscavengers. J. Water Process Eng. 2018, 24, 63–73. [Google Scholar] [CrossRef]
- Liosis, C.; Karvelas, E.G.; Karakasidis, T.; Sarris, I.E. Numerical study of magnetic particles mixing in waste water under an external magnetic field. J. Water Supply Res. Technol. 2020, 1–10. [Google Scholar] [CrossRef]
- Karvelas, E.; Liosis, C.; Benos, L.; Karakasidis, T.; Sarris, I. Micromixing efficiency of particles in heavy metal removal processes under various inlet conditions. Water 2019, 11, 1135. [Google Scholar] [CrossRef]
- Karvelas, E.G.; Lampropoulos, N.K.; Sarris, I.E. A numerical model for aggregations formation and magnetic driving of spherical particles based on OpenFOAM®. Comput. Methods Programs Biomed. 2017, 142, 21–30. [Google Scholar] [CrossRef] [PubMed]
- Sofos, F.; Liakopoulos, A.; Karakasidis, T.E. Particle-Based modeling and meshless simulation of flows with smoothed particle hydrodynamics. Glob. NEST J. 2019, 21, 513–518. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620. [Google Scholar] [CrossRef]
- Ramesha, D.K.; Anvekar, A.; Raj, A.; Vighnesh, J.; Tripathi, S. A DSMC analysis of gas flow in micro channels using OpenFOAM. In Proceedings of the International Conference on Advances in Mechanical Engineering Sciences (ICAMES-17), Mandya, Karnataka, 21–22 April 2017. [Google Scholar]
- Tijskens, E.; Ramon, H.; Baerdemaeker, J.D. Discrete element modelling for process simulation in agriculture. J. Sound Vib. 2003, 266, 493–514. [Google Scholar] [CrossRef]
- Cao, Q.; Han, X.; Li, L. An active microfluidic mixer utilizing a hybrid gradient magnetic field. Int. J. Appl. Electromagn. Mech. 2015, 47, 583–592. [Google Scholar] [CrossRef]
- Yoo, J.; Kim, H.S.; Park, S.Y.; Kwon, S.; Lee, J.; Koo, J.; Seo, Y.S. Instantaneous integration of magnetite nanoparticles on graphene oxide assisted by ultrasound for efficient heavy metal ion retrieval. Ultrason. Sonochem. 2020, 64, 104962. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Ni, S.; Wang, X.; Zhang, W.; Lagerquist, L.; Qin, M.; Willför, S.; Xu, C.; Fatehi, P. Ultrafast adsorption of heavy metal ions onto functionalized lignin-based hybrid magnetic nanoparticles. Chem. Eng. J. 2019, 372, 82–91. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).