Numerical Modeling on Fate and Transport of Pollutants in the Vadose Zone ^†

Abstract

Soil contamination is an issue of paramount importance to assess human health (HHRA) as well as ecological (ERA) risk assessment. To analyze risk scenarios related to contaminated soils, the identification of sources, either of primary or secondary type, as well as the assessment of propagation and fate processes is needed. Although many studies refer to the transport of pollutants in fully saturated porous media, little efforts have been made concerning the case of partially saturated soils so far. The matter is of interest as the contamination in the fully saturated region may take place as a result of the percolation in the vadose zone. Governing equations ruling fate and transport processes in partially saturated soils are here solved numerically by means of a finite element method approach. Richards equations are adopted to describe flow dynamics through the hydraulic conductivity coefficient K_s, while contaminant fate is mainly described by the sorption coefficient K_p. As for the boundary conditions, we consider a local and continuous spill of contaminant at the upper ground of variable thickness. Precipitations are given as step functions whose intensity is derived by considering pluviometric data at the station of Gròmola, Campania Region, Italy. Benzene and tetrachloroethylene (PCE) are taken into account. A comparative analysis is carried out for permeability K_s and distribution K_d coefficients in the range [10⁻⁶, 10⁻⁴] m/s and [10⁻⁵, 10⁻³] m³/kg. Results are then compared and discussed.

1. Introduction

One of the attention-seeking environmental issues are related to the contamination of groundwater bodies caused by the release of pollutants, moving through the unsaturated zone, i.e., the vadose zone, to the point of possibly reaching the underlying aquifer. Two types of sources are generally acknowledged: non-point sources from agricultural activities (fertilizers, pesticides, and fumigants) and point-source (solid waste disposal, underground leaking from storage tanks, chemicals spills, etc.) [1]. These sources represent a relevant threat because they may damage public water supply and compromise aquatic ecosystems in discharge zones, due to the toxicity of the involved contaminants [2,3]. Within the framework of groundwater risk assessment and remediation of contaminated sites, models for simulating contaminants transport in the unsaturated zone are increasingly explored and required [4,5]; the breakthrough concentration curve measured at a certain point of assessment is one of the main useful modeling outputs [6,7].

The aspects involved in the fate and transport processes occurring in the unsaturated zone are complex and interrelated: Contaminants with different physicochemical properties are carried in air and water phases by different transport mechanisms (advection and dispersion-diffusion). While moving, they may be simultaneously affected by reaction processes (sorption, abiotic transformation, biodegradation, etc.) [8]. The effectiveness of a fate and transport model in the unsaturated medium relies on an adequate characterization of the site, as soil properties strongly affect hydrological, physical–chemical, as well as biological processes [9,10,11].

In the scientific literature, several approaches are proposed as an attempt to model fate and transport mechanisms of pollutants in soils. They range from basic approaches characterized by a high level of simplification and a limited number of input parameters to more complex paradigms, able to reproduce heterogeneous and anisotropic media or multicontaminant systems, needing a large and more accurate input dataset. A possible approach to deal with the problem is to assume a steady flow, specifically a constant seepage water infiltration rate, to be given as a flow boundary condition [12]. This hypothesis is either chosen to simplify the mathematics or in the absence of transitory phenomena. For example, analytical solutions are mainly based on partial differential equations (PDEs) with constant coefficients, that is, they are written in the case of uniform and steady velocity. However, a steady flow hypothesis may lead to an improper estimate of the contaminant concentration over the time. Different authors [12,13,14] have analyzed the effects of temporal infiltration variability on the downward migration of contaminants. Kuntz and Grathwohl [12] state that extreme infiltration events lead to higher pollutant concentrations in transient simulations because the short residence time of seepage water reduces biodegradation and sorption.

In this paper, the results of a numerical investigation, based on a local and continuous spill of a contaminant on the ground surface of an unsaturated soil column, are presented. The differences in the modeled contaminant concentration caused by different infiltration scenarios are discussed. Results are compared considering two different contaminants (benzene and tetrachloroethylene). Permeability K_s [m/s] and distribution K_p [m³/kg] coefficients are varied in the range [10⁻⁶, 10⁻⁴] and [10⁻⁵, 10⁻³], respectively. The breakthrough concentration curves obtained at different depths for the different scenarios are compared and discussed.

2. Theoretical Framework

A two-dimensional isothermal model, based on the coupling of flow and transport equations in the unsaturated soil region, is here adopted to run the numerical simulations. The software package COMSOL Multiphysics^® [15] is used for this purpose. The unsaturated water flow is described by a more general variant of Richards’ equations [16], developed by Bear [17], which takes into account time-dependent changes in both saturated and unsaturated conditions. The formulation is presented in Equation (1) where the pressure p is the dependent variable:

$$\rho \left(\frac{C_m}{\rho g}+S_{e}S\right)\frac{\partial p}{\partial t}+\nabla ·\rho \left(-\frac{k_s}{\mu }{k}_r\left(\nabla p+\rho g\nabla z\right)\right)=Q_m$$

(1)

The meaning of symbols is as follows: C_m [m⁻¹] is the specific moisture capacity (ability of soils and rocks to yield or to gain moisture with changing pressure head, that is, the slope of the soil–water retention curve), S_e is the effective saturation [-], S is the storage coefficient, k_s is the saturated permeability [m²/s], k_r is the relative permeability [-], µ [Pa s] is the dynamic viscosity, ρ [kg/m³] is the fluid density, g = 9.80665 m/s² is the acceleration gravity, z is the local elevation, and Q_m [kg/(m³ s)] is the fluid source or sink (specific mass flux).

The hydrological behavior of the unsaturated medium can be described by the soil water characteristic function, i.e., the relation between the volume of water retained by the soil $\theta$ [m³/m³] and the governing suction forces, and the hydraulic conductivity function, i.e., the relation between $\theta$ and the relative hydraulic conductivity K. These relations are strongly nonlinear. In the scientific literature, different empirical models are presented [18]. Here, the widely used van Genuchten formulation is chosen [19,20] (Equations (2)–(5)):

$$\theta \left(z\right)={\theta }_r+S_e\left({\theta }_s-{\theta }_r\right)$$

(2)

$$S_e={\left[1+{\left|\alpha H_p\right|}^n\right]}^{-m}$$

(3)

$$C_m=\frac{\alpha m}{1-m}\left({\theta }_s-{\theta }_r\right)S_e{}^{\frac{1}{m}}{\left(1-S_e{}^{\frac{1}{m}}\right)}^m$$

(4)

$$K=S_e^{1/2}{\left[1-{\left(1-S_e^{1/m}\right)}^m\right]}^2$$

(5)

where ${\theta }_r$ and ${\theta }_s$ are the residual and saturated water contents, H_p is the pressure head, α > 0 is a parameter to scale the pressure head, and n and m = 1 − 1/n are dimensionless parameters.

The fate and transport problem is evaluated by combining previous Equations (2)–(5) with an advection–dispersion equation (ADE) written for the generic specie (Equation (6)):

$$\frac{\partial C}{\partial t}+\nabla ·\left(-\mathit{D}\nabla C_w\right)+\mathit{u}·\nabla C_w=R$$

(6)

where C_w is the aqueous contaminant concentration, D is the diffusion tensor which combines mechanical dispersion and molecular diffusion and depends mainly on the tortuosity of the medium and the travel distance (for further information see [21,22]), u is the local flow velocity vector, calculated by solving Equation (1), and R is the reaction rate for the contaminant. Chemical and biochemical processes can be considered negligible for the case at hand; therefore, R is assumed equal to zero.

The C_w parameter is included in the general mass balance equation, which takes into account the occurrence of the contaminant in three phases: solid, aqueous, and gaseous. In the presented model, the contaminant volatility is neglected; hence, the only considered phase change is between the solid and aqueous phase. The relationship between solid concentration C_s and aqueous concentration C_w, ruled by adsorption phenomena, is described by an equilibrium isotherm model. Many models with different degrees of approximation have been developed over the years [23]; a linear sorption isotherm is chosen, where C_s is directly proportional to C_w, through the distribution coefficient K_d:

$$C_s=K_d{C}_w$$

(7)

The assumption of linear isotherm is justified for the selected contaminants. In fact, several nonpolar organic contaminants have a linear or close to linear sorption behavior [24]. A common assumption for organic contaminants is that sorption only occurs with organic material [25] and, therefore, the distribution coefficient K_d can be expressed by Equation (8):

$$K_d=f_{oc}{K}_{oc}$$

(8)

where f_oc is the organic carbon fraction in the soil and K_oc is the organic carbon–water partition coefficient.

The precipitation regime is evaluated by keeping constant the annual effective infiltration, the latter obtained by subtracting the monthly potential evapotranspiration from the monthly measured precipitation. The potential evapotranspiration in the j-month et_pj is computed as a function of the average monthly temperature t_j (°C) using the empirical method proposed by Thornthwaite [26] as:

$$e{t}_{pj}=16,2 k_j{\left(\frac{10}{I}{t}_j\right)}^a$$

(9)

where k_j is the radiation coefficient in the jth-month, I is the annual thermal index, and a is an empirical coefficient function of I:

$$I={\displaystyle \sum }_{j=1}^{12}{\left(\frac{t_j}{5}\right)}^{1,514}$$

(10)

$$a=0.49239+1.792\times {10}^{-2}·I-7.71\times {10}^{-5}·I^2+6.75\times {10}^{-7}·I^3$$

(11)

3. Materials and Methods

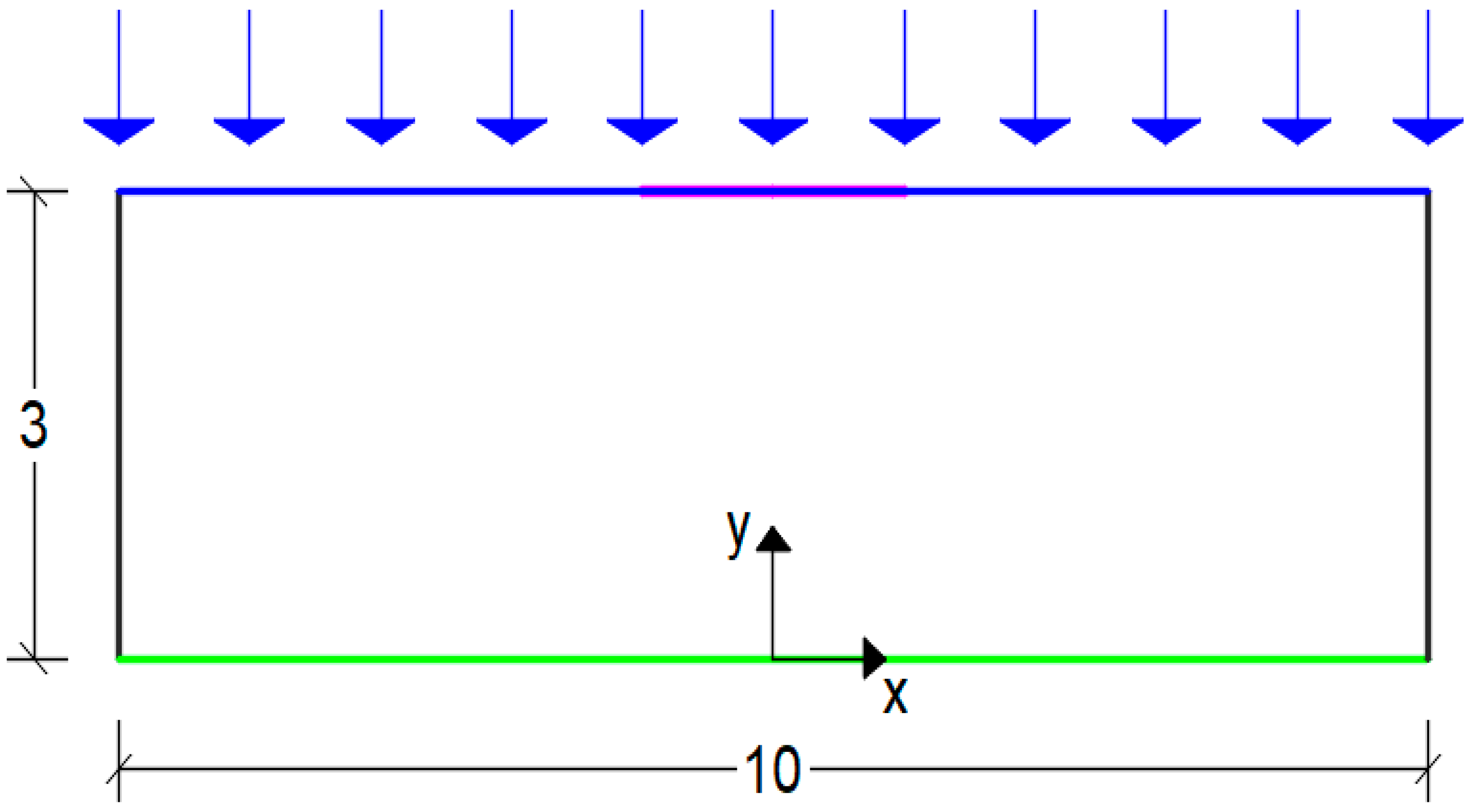
3.1. Setup of the Numerical Model

The implemented numerical model aims to reproduce migration through the vadose zone of an organic contaminant from a continuous source to the water table. The domain consists of a vertical column of soil, 10 m wide and 3 m high (Figure 1). As regards flow conditions, the initial distribution of pressure head is here assumed to be hydrostatic with the atmospheric pressure head at the water table; the top boundary condition is assumed to be of Neumann type—specifically, a constant or a transient inflow is set according to the selected precipitation scenario (blue arrows in Figure 1). At the initial time, the soil domain is assumed to be uncontaminated; therefore, the initial liquid phase concentration C_w (t = 0) is zero. A continuous source of contaminant with a concentration equal to 0.1 mg/L is placed on the ground surface. The contaminant is assumed to be non-volatile and non-reacting, and therefore, the degradation kinetic rate is equal to zero.

Meshing is performed by discretizing the computing domain in quadrilateral elements. Different mesh dimensions are tested, ranging from 0.1 to 0.03 m, to evaluate the convergence of the results. From the analysis, the dimension of 0.08 m is selected to achieve best accuracy while optimizing the computation time.

3.2. Comparison Methodology

Different simulations of contaminants transport are carried out concerning two substances with different physical behavior: benzene, a light non-aqueous liquid (LNAPL) belonging to aromatic hydrocarbons, and tetrachloroethylene (PCE), a dense non-aqueous liquid (DNAPL) falling within chlorinated solvents.

For each contaminant, four precipitation scenarios are set with a simulation period of two years. Keeping constant the annual effective infiltration as previously said, the infiltration is set in time according to two distributions: a non-varying, i.e., constant trend and a step-wise function where the annual precipitation is concentrated over a fixed period of time (Dt), shorter than a year, repeating itself periodically. Three Dt are taken into account: a three-, five-, and eight-month period, respectively. Data used for the analysis are taken from the pluviometric station of Gròmola, Campania Region, Italy.

Finally, the effects of the hydraulic conductivity and distribution coefficient on contaminant migration are evaluated considering three values of K_s [m/s], 10⁻⁶–10⁻⁵–10⁻⁴, and three values for K_d [m³/kg], 10⁻⁵–10⁻⁴–10⁻³. Each contaminant was then simulated for 36 cases, representing the different combinations of precipitation scenarios, hydraulic conductivity and distribution coefficient values, in order to assess the output effects as well as the sensitivity of the model to the variability of the input parameter.

The source concentration C_w0 is set equal to 100 µg/L for both the contaminants. Their physicochemical properties are derived from the database of the Italian National Institute of Health [27] and reported in

Table 1. Physical–chemical characteristics of the selected contaminants.

Parameter	Measurement Unit	Values
		Benzene	Tetrachloroethylene
Molecular weight	g/mol	78.1	165.8
Solubility (S)	mg/L	1750	200
Diffusion coefficient in water (Dw)	cm2/s	9.80 × 10−6	8.20 × 10−6

.

The longitudinal dispersivity α_l is calculated as a function of the travel distance, using the Gelhar relationship [28] (Equation (10))

$$ln{\alpha }_l=-4.933+3.811ln{z}_m\hspace{1em}\hspace{1em}\hspace{1em}{z}_m\le 2$$

(12a)

$$ln{\alpha }_l=-2.727+0.584ln{z}_m\hspace{1em}\hspace{1em}\hspace{1em}{z}_m\ge 2$$

(12b)

where z_m is the distance from the source to the observation location. In this case, z_m is fixed equal to 3 m, and hence, α_l is equal to 0.125. The transverse dispersivity is assumed to be a tenth of the longitudinal one, i.e., 0.0125.

A sandy loam soil, according to the United States Department of Agriculture (USDA) classification, is selected. The parameter values for this soil are derived from [29] and listed in

Table 2. Soil parameter values.

Parameter	Measurement Unit	Values
Soil bulk density (ρb)	kg/m3	1700
Saturated water content (θs)	-	0.41
Residual water content (θr)	-	0.065
Van Genuchten parameter (α)	-	0.075
Van Genuchten parameter (n)	-	1.89

.

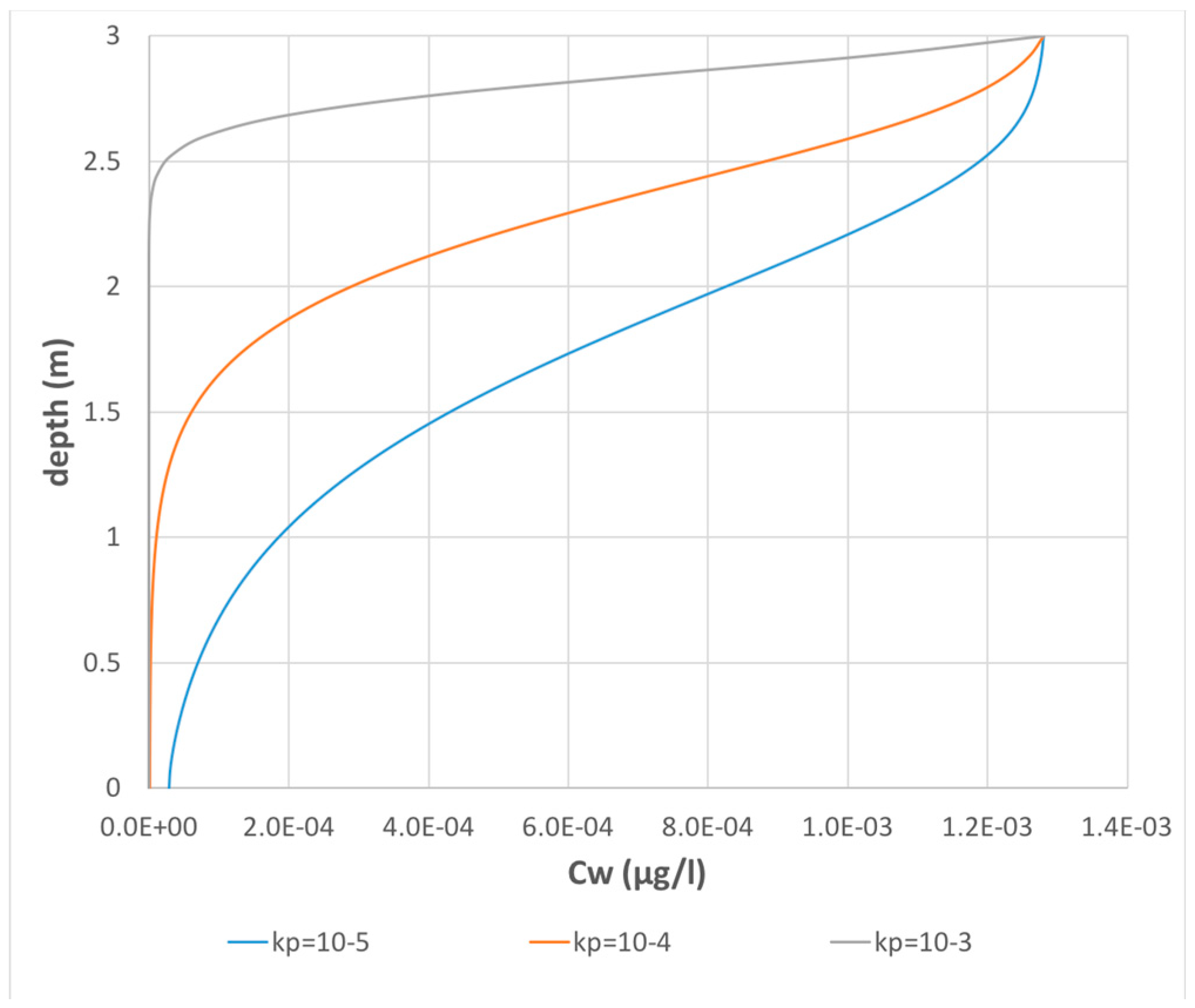
4. Results and Discussion

In order to provide a first overview of the differences between the four precipitation scenarios, the values of C_w at a given time have been calculated as a function of the depth from the ground surface (Figure 2).

The 72 simulations exhibit similar trends: With the same distribution coefficient K_d, the two contaminants have similar concentration values, demonstrating the importance of these values with respect to others, such as the diffusion coefficient; the difference between steady and transient flow is significant, while the difference between the three transient distributions is not very pronounced. Furthermore, all the different contamination scenarios show the typical bell-shaped curve, and all curves intersect at the same point. As an example, in Figure 3 the graphs of the concentration on the 360th day with a K_s equal to 10⁻⁶ and K_d equal to 10⁻⁵ for benzene and tetrachloroethylene are reported.

Another comparison is developed between different distribution coefficient K_d, for the same contaminant and precipitation scenario. The analysis shows that contaminant concentration is significantly influenced by the variation of K_d. In Figure 3, the comparison between the benzene concentration obtained from the three values of K_d for a constant precipitation is shown. The graph shows that the contaminant travel distance after 360 days for a K_d value of 10⁻⁵–10⁻⁴–10⁻³ is about 0.6, 2.8, and more than 3 m, respectively.

For a better understanding of the migration trends, the values of C_w over time at three different depths (2, 1, and 0.5 b.g.s) are calculated. The graph concerning benzene concentration is reported in Figure 4.

The assessment of concentration over a time period of two years for the four precipitation scenarios (Figure 4) allowed us to obtain the following:

• Three families of four curves each, the first one relating to the depth of 2 m in shades of blue, the second one relating to the depth of 1 m in shades of orange, and the third one relating to the depth of 0.5 m in shades of green. The i-th family (i = 1, …, 4) is related to the constant precipitation and the transient precipitation with a 3 months’ step, 5 months’ step, and 8 months’ step;
• Each family of curves has the same inflexion point;
• Curves follow a similar trend, with an initial concavity upwards and a final concavity downwards;
• The effects of the different precipitation scenario are not predominant, compared to the remaining parameters being investigated.

5. Conclusions

A local and continuous spill of a contaminant on the ground surface of an unsaturated soil column was here investigated numerically. Thirty-six cases per contaminant (72 simulations in total) were run, representing different combinations of precipitation scenarios, hydraulic conductivity K_s values, and distribution coefficient K_d values. The aim was to assess the effects on the results of a steady or a transient infiltration flow as well as by changing K_s and K_d.

Three families, corresponding to depths z = 0.5, 1.0, and 2.0 m, of four curves (uniform infiltration and step-wise infiltration functions on 3, 5, and 8 months, respectively) were derived. It was observed that different precipitation scenarios did not have significant effects on the concentration outputs, probably because the stepwise function used in this study does not actually represent extreme infiltration events, which have major impacts on contaminant migration. Interestingly, each family of curves exhibited the same inflexion point in addition to a similar trend of the curves, with an initial concavity upwards and a final concavity downwards. The results show a significant effect of the distribution coefficient K_d on the modeled concentration and the travel distances, confirming that sorption phenomena have a key role in the fate and transport processes.