Abstract
In recent years, use of the stochastic model has been growing due to the high complexity and dynamics of the atmosphere, especially the rainfall process. Various concepts have been applied to rainfall modeling, ranging from simplistic approaches to more complex models. It is important to understand different stochastic rainfall modeling approaches, as well as their advantages and limitations. This paper determines the development of the latest stochastic rainfall models in the Asia region, where different concepts of stochastic rainfall models were highlighted. It reviews the different methodologies used, including rainfall forecasting, spatio-temporal analysis, and extreme event. We select 30 articles from 1571 literature published between 2013–2022 from the Scopus database. The results show that the stochastic models often used in the literature consist of Markov chain, weather generator, probability distribution, ARIMA, and the Bayesian model. In the recent development in Asia, stochastic models in rainfall modeling research are widely used to generate the occurrence and amount of rainfall data, statistical downscaling, future rainfall trends, and estimation of extreme values. The difference in spatio-temporal, climate conditions, and the parameters model can cause the performance of each model to be different.
1. Introduction
The development of a climate model is an attempt to simplify the understanding of the climate system. Stochastic models are now an important topic in climate research, and are starting to be widely used in more comprehensive climate predictions. Stochastic methods for numerical weather and climate predictions allow for an accurate representation of uncertainty, reduced bias, and improved representation of long-term climate variability. Research related to systematic reviews of stochastic climate models, especially rainfall models, is not yet available for the Asia region. Assessing the accuracy of the output from these models will provide an overview of the robustness of the stochastic model in representing the rainfall model.
2. Methodology
The authors used the preferred reporting items for systematic reviews and meta-analyses (PRISMA) approach to search and select the literature samples. PRISMA has 3 steps [1]: (1) identification, (2) screening, and (3) included. This study mainly focused on the stochastic climate model in Asian countries. After the screening process, we chose 30 articles representing 14 different journals, including the Journal of Hydrology (23%), the International Journal of Climatology (13%), and Theoretical and Applied Climatology (13%). The flow chart is shown in Figure 1.
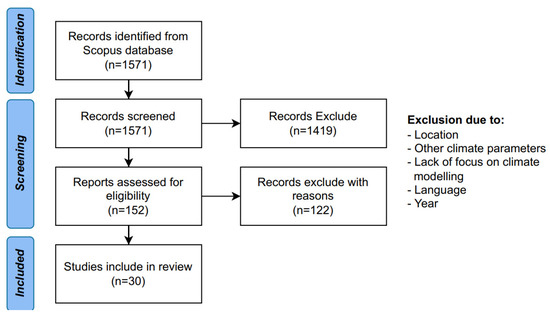
Figure 1.
Flowchart outlining protocol of review using PRISMA.
3. Results
Several studies mostly used stochastic rainfall models for downscaling rainfall data [2,3,4,5] and generating the occurrence and amount of rainfall data [6,7,8,9,10]. Regression models and stochastic weather generators are the most widely used statistical-downscaling methods [3,4]. The Markov chain is the most popular technique to generate rain occurrence because it is easy and simple [5,6,8,9]. Meanwhile, a probability distribution generates rainfall amounts [2,6,9].
3.1. Markov Chain
The Markov chain defines the state of a particular day as a “wet” or “dry” day and describes the relationship between today’s state and the previous day’s. The use of previous rainfall data was quite varied, such as 1 day [2,6], 0–3 days [8], and 0–5 days before [9]. Most of the Markov chain models mentioned in the literature are first-order models. Although the first-order is satisfactory, the most prolonged simulated dry spell results were slightly shorter than the observed results, which may be due to the short-term memory of the first-order Markov model [6]. The solution is to use a Markov chain of order two or higher to overcome this limitation. In tropical areas such as Malaysia, the second-order Markov chain has the most optimum value for estimating monthly rainfall, while the third-order is best for estimating annual rainfall [9]. Meanwhile, in sub-tropical areas, which have four seasons, the prediction of daily rainfall in summer is better than in other seasons [8].
Along with the development of stochastic model research, the use of Markov chain models has been modified to improve their accuracy, such as modified Markov models (MMM) [2], the hidden Markov model (HMM) [11], non-hidden homogeneous Markov models (NHMM) [12], decadal and hierarchical Markov chain (DHMC) [13], and the stochastic daily rainfall model—Markov chain rainfall event model (SDRM-MCRE) [5]. MMM includes atmospheric predictors that predict the effects of changing climatic conditions and other variables to represent specific rainfall characteristics. HMM contains hidden and unknown parameters (event). Compared with the HMM, the NHMM model introduces non-homogeneity by allowing for different components in the transition matrix or the emission matrix, depending on other relevant variables. SDRM-MCRE can comprehensively maintain the rainfall characteristics of the rainfall time series (e.g., monthly mean rainfall and extreme rainfall percentiles) and rainfall event characteristics (e.g., different classes of rainfall duration, rainfall depth, rainfall intensity, and drought).
3.2. Probability Distribution
Parametric probabilities, usually used to generate rainfall amounts, include one-parameter distributions, such as exponential [6,9], two-parameter distributions, such as gamma [2,5,6,9,13], Weibull [6,14], normal/Gaussian [2,12], log-normal [9], and the distribution of three parameters, such as mixed exponential [6,9,14], hybrid exponential [6,9,11], and normal skewed [6,9]. Meanwhile, K-nearest neighbor is commonly used in nonparametric probabilities [10].
Most studies state that distribution with three parameters shows better results than other models [6,14]. Three-parameter distributions, especially the mixed exponential distribution, perform better in reproducing the daily rainfall variance in subtropical regions such as China. In contrast, the skewed normal and Weibull distributions better simulate extreme rainfall characteristics at the >95th percentile [6]. In the tropics, mixed exponential (three parameters) is very suitable for estimating the average and maximum values on an hourly scale quite well, compared with Weibull (two parameters) [14].
Spatiotemporal differences also affect the application of the distribution model, so that not all three-parameter distributions are always better. For example, in the Kelantan watershed, Malaysia, the mixed exponential distribution was not chosen as the best distribution. Statistical tests proved no significant difference between the performance of one, two, and three-parameter distributions [9]. At extreme values, the exponential (one parameter) and log-normal (two parameters) distributions perform better than other distributions [9], while the double gamma distribution (two parameters) can capture extreme rainfall as well as average rainfall at the same time [5].
3.3. Stochastics Weather Generator
Different types of weather generators use two approaches, namely the Markov chain [6,7,15] and spell length [3,7]. The Markov chain approaches, such as WGEN, CLIMGEN, CLIGEN, WeaGETS, and MulGETS, and spell length approaches, such as LARS-WG, are the most widely used. From several studies, models based on the spell length approach, such as LARS-WG, have worse performance than Markov chain-based models, such as WeaGETS [7] and SDSM, a hybrid model that combines a regression model and stochastic weather generators [3].
Chen and Brissette [7] compared five weather stochastics to generate rainfall data in China’s Loss Plateau. The WGEN, CLIMGEN, and CLIGEN use first-order 2-state Markov chains to generate precipitation events. In calculating the amount of rainfall, WGEN uses the gamma, CLIMGEN uses the Weibull, while CLIMGEN uses the skewed normal. WeaGETS uses a combination of third-order Markov chains and a mixed exponential distribution. For simulating daily rainfall amounts, weather generators based on three-parameter (CLIGEN and WeaGETS) generally perform better than two-parameter distributions (WGEN and CLIMGEN), especially in simulating extreme rainfall.
Stochastics weather generators commonly used for multisite are MSRG [16], MulGETS [17], and the new multivariate-multisite WG [18]. MSRG can simultaneously simulate the spatial dependence of the occurrence and amount of multisite daily rainfall using the SSRN method. MSRG also has the potential to be applied in relatively large basins or areas [16]. MulGETS is an extension of SSWG, created by driving a single site model with temporally dependent and spatially correlated random numbers. Ahn [18] combined annual and daily weather generators to overcome the limited variability of low-frequency climate variables and generate extreme rainfall events.
The STREAP WG model for remote sensing data such as radar [19] was used to measure the sub-pixel variability of the radar from extreme rainfall to downscaling the radar rainfall recorded at a particular pixel. Peleg and Morin [20] developed a slightly different WG based on a rainfall field analysis derived from weather radar data, in addition to synoptic parameters that explicitly represented convective rain cell elements that are known to have a significant impact on the catchment hydrological response. HiReS-WG is used to periodically generate rain fields with a high spatial and temporal resolution.
3.4. ARIMA
ARIMA is a typical statistical analysis model that uses time-series data to predict future trends. The ARIMA model approach can outperform most other statistical models, such as in hydrological time series. The relative advantage of the ARIMA model is due to its statistical nature, as well as the well-known methodology in building the model [21]. The ARIMA model is a combined model between autoregressive (AR) and moving average (MA) as well as an order-d differencing process for data at seasonal and non-seasonal levels, and is included in the linear forecasting group [8]. The ARIMA model is a model that has been widely applied in rainfall data analysis for various purposes, especially in drought analysis [21,22]. The ARIMA model is a time series forecasting approach.
3.5. Bayesian
The Bayesian approach is used in many hydrological studies, such as uncertainty quantification, water quality modeling, and hydroclimatic analysis. One of the studies was carried out by developing a Bayesian model to evaluate changes in the maximum thickness of seasonally frozen ground (MTSFG) [23]. The application of this Bayesian method has been used to estimate snow depth and soil organic carbon content in permafrost areas using the Markov chain Monte Carlo (MCMC) sampling method [24,25].
Currently, the use of the Bayesian model has been modified to improve its accuracy in rainfall analysis. Some of those mentioned in the literature are the Gaussian copula model, the Bernoulli-Gamma hierarchical Bayesian model, and the Bayesian-time varying downscaling model (TVDM). The Gaussian copula model has been optimalisationto explore future extreme rainfall changes [26]. In addition, this Gaussian copula can be used as a new scheme to correct for biases in the spatial correlation as well as the marginal distribution of the simulated rainfall. The Bernoulli-Gamma hierarchical Bayesian model was used to simulate rainfall to build a hierarchical Bayesian mixture model for daily rainfall forecasts, using endogenous and external information [27]. The proposed Bayesian-time varying downscaling model (TVDM) is used to derive monthly rainfall in India using the large-scale output of general circulation models (GCM). The methodology proposed by the TVDM was developed using a Bayesian approach in updating the parameters previously adopted in the Bayesian dynamic linear model.
3.6. Strengths and Limitation Model
The Markov chain has the advantages of being easy to use, able to simulate rainfall in the station network while maintaining influential spatial attributes, maintaining rainfall characteristics from the rainfall time series, having great potential to be used for flood and drought risk assessment, and being able to simulate monthly and annual rainfall events. The ARIMA model in the literature is mainly carried out in dry areas (Pakistan, Saudi Arabia, and Iraq). This is because ARIMA can forecast drought on different timescales and outperform most other statistical models. The model’s weakness is that it cannot predict for long periods. The WG model is excellent for generating data in small areas. The Bayesian model found in this literature review contains pure Bayesian but also a combination model, such as TVDM and the Bayesian NHMC. WGs are appropriate for climate change projections because their time-varying components allow for variations in transition probabilities or emission probabilities depending on external factors. In the k-nearest neighbor resampling, little effort is needed to estimate the parameter. This model can be an excellent alternative to simulating multisite pre-precipitation events. The strengths and limitations of the stochastic model is shown in Table 1.

Table 1.
Strengths and limitations of the stochastic model.
4. Conclusions
Research related to stochastic models on rainfall modeling in the Asia region is a very complex study. The variety of scopes, approaches, focuses, methodologies, and limitations used in rainfall modeling hinders a common understanding of the stochastic models used. The results of the study indicate that the research objectives of using stochastic models in rainfall modeling research include climate data generation, statistical downscaling, predicting future rainfall trends, the estimation of extreme values, and so on. Of these purposes, the stochastic model is the most widely used for climate data generation and statistical downscaling. The rainfall data generator is used to estimate the occurrence and amount of rainfall. Various stochastic models that are often used in the literature consist of Markov chain, weather generator, probability distribution, ARIMA, and the Bayesian model. The performance of these stochastic models will be different for each region in Asia. The spatiotemporal differences, the study area, and the use of parameters can be the cause of the difference in the results of each model. The stochastic model is easy and good to use, and the temporal, spatial scale, and type of model can be adapted to the research objectives, where the more combinations of models, the better the results. Therefore, in general, the stochastic model is very flexible depending on user needs.
Author Contributions
Conceptualization, H.A.P. and P.; methodology, H.A.P.; formal analysis, H.A.P., E.D.P.S., H.N. and M.R.; data curation, E.D.P.S. and H.N.; writing—original draft preparation, H.A.P., E.D.P.S., H.N. and M.R.; writing—review and editing, H.A.P. and H.N.; visualization, M.R.; supervision, P. and A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are grateful for the support from IPB University, Bogor, Indonesia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. Int. J. Surg. 2021, 88, 105906. [Google Scholar] [CrossRef] [PubMed]
- Mehrotra, R.; Sharma, A.; Kumar, D.N.; Reshmidevi, T.V. Assessing future rainfall projections using multiple GCMs and a multi-site stochastic downscaling model. J. Hydrol. 2013, 488, 84–100. [Google Scholar] [CrossRef]
- Hassan, Z.; Shamsudin, S.; Harun, S. Application of SDSM and LARS-WG for simulating and downscaling of rainfall and temperature. Theor. Appl. Climatol. 2014, 116, 23–257. [Google Scholar] [CrossRef]
- Forsythe, N.; Fowler, H.J.; Blenkinsop, S.; Burton, A.; Kilsby, C.G.; Archer, D.R.; Harpham, C.; Hashmi, M.Z. Application of a stochastic weather generator to assess climate change impacts in a semi-arid climate: The Upper Indus Basin. J. Hydrol. 2014, 517, 1019–1034. [Google Scholar] [CrossRef]
- Gao, C.; Booij, M.J.; Xu, Y. Development and hydrometeorological evaluation of a new stochastic daily rainfall model: Coupling Markov chain with rainfall event model. J. Hydrol. 2020, 589, 125337. [Google Scholar] [CrossRef]
- Li, Z.; Brissette, F.; Chen, J. Assessing the applicability of six precipitation probability distribution models on the Loess Plateau of China. Int. J. Climatol. 2014, 34, 462–471. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P. Comparison of five stochastic weather generators in simulating daily precipitation and temperature for the Loess Plateau of China. Int. J. Climatol. 2014, 34, 3089–3105. [Google Scholar] [CrossRef]
- Wei, W.; Yan, Z.; Jones, P.D. Potential predictability of seasonal extreme precipitation accumulation in China. J. Hydrol. 2017, 18, 1071–1080. [Google Scholar] [CrossRef]
- Ng, J.L.; Aziz, S.A.; Huang, Y.F.; Wayayok, A.; Rowshon, M.K. Generation of a stochastic precipitation model for the tropical climate. Theor. Appl. Climatol. 2017, 133, 489–509. [Google Scholar] [CrossRef]
- Lee, T.; Singh, V.P. Discrete k-nearest neighbor resampling for simulating multisite precipitation occurrence and model adaption to climate change. Geosci. Model Dev. 2019, 12, 1189–1207. [Google Scholar] [CrossRef]
- Patidar, S.; Tanner, E.; Soundharajan, B.; Sengupta, B. Associating climatic trends with Stochastic modeling of flow sequences. Geosciences 2021, 11, 255. [Google Scholar] [CrossRef]
- Long, Y.; Tang, R.; Wang, H.; Jiang, C. Monthly precipitation modeling using Bayesian non-homogeneous hidden Markov chain. Hydrol. Res. 2019, 50, 562–576. [Google Scholar] [CrossRef]
- Chowdhury, A.F.M.K.; Kar, K.K.; Shahid, S.; Chowdhury, R.; Rashid, M.M. Evaluation of spatio-temporal rainfall variability and performance of a stochastic rainfall model in Bangladesh. Int. J. Climatol. 2019, 39, 4256–4273. [Google Scholar] [CrossRef]
- Abas, N.; Daud, Z.M.; Yusof, F. A comparative study of mixed exponential and Weibull distributions in a stochastic model replicating a tropical rainfall process. Theor. Appl. Climatol. 2014, 118, 597–607. [Google Scholar] [CrossRef]
- Chen, J.; Chen, H.; Guo, S. Multi-site precipitation downscaling using a stochastic weather generator. Clim. Dyn. 2018, 50, 1975–1992. [Google Scholar] [CrossRef]
- Ahn, K. Coupled annual and daily multivariate and multisite stochastic weather generator to preserve low- and high-frequency variability to assess climate vulnerability. J. Hydrol. 2020, 581, 124443. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, A.; Wang, L.; Fu, G.; Chen, D.; Liu, C.; Cai, T. Projecting streamflow in the Tangwang River basin (China) using a rainfall generator and two hydrological models. Clim. Res. 2015, 62, 79–97. [Google Scholar] [CrossRef]
- Peleg, N.; Marra, F.; Fatichi, S.; Paschalis, A.; Molnar, P.; Burlando, P. Spatial variability of extreme rainfall at radar subpixel scale. J. Hydrol. 2016, 556, 922–933. [Google Scholar] [CrossRef]
- Peleg, N.; Morin, E. Stochastic convective rain-field simulation using a high-resolution synoptically conditioned weather generator (HiReS-WG). Water Resour. Res. 2014, 50, 2124–2139. [Google Scholar] [CrossRef]
- Mossad, A.; Alazba, A.A. Drought forecasting using stochastic models in hyper-arid climate. Atmosphere 2015, 6, 410–430. [Google Scholar] [CrossRef]
- Kumar, P.; Shah, S.F.; Uqaili, M.A.; Kumar, L.; Zafar, R.F. Forecasting of drought: A case study of the water-stressed region of Pakistan. Atmosphere 2021, 12, 1248. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, J.; Yang, D.; Wang, T. Estimating seasonally frozen ground depth from historical climate data and site measurements using a bayesian model. Water Resources Res. 2018, 54, 4361–4375. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Liljedahl, A.K.; Dafflon, B.; Ulrich, C.; Peterson, J.E.; Gusmeroli, A.; Hubbard, S.S. Mapping snow depth within a tundra ecosystem using multiscale observations and Bayesian methods. Cryosphere 2017, 11, 857–875. [Google Scholar] [CrossRef]
- Tran, A.P.; Dafflon, B.; Hubbard, S.S. Coupled land surface–subsurface hydrogeophysical inverse modeling to estimate soil organic carbon content and explore associated hydrological and thermal dynamics in the Arctic tundra. Cryosphere 2017, 11, 2089–2109. [Google Scholar] [CrossRef]
- So, B.; Kim, Y.; Kwon, H.; Lima, C.H.R. Stochastic extreme downscaling model for an assessment of changes in rainfall intensity-duration-frequency curves over South Korea using multiple regional climate models. J. Hydrol. 2017, 553, 321–337. [Google Scholar] [CrossRef]
- Kim, M.; Yhang, Y.; Lim, C. Gaussian copula method for bias correction of daily precipitation generated by a dynamical model. J. Appl. Meteor. Climatol. 2018, 58, 269–289. [Google Scholar] [CrossRef]
- Pichuka, S.; Maity, R. Development of a time-varying downscaling model considering non-stationarity using a Bayesian approach. Int. J. Climatol. 2018, 38, 3157–3176. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).