Comparative Analysis of Voltage Stability in Radial Power Distribution Networks Under Critical Loading Conditions and Diverse Load Models

Abstract

Modern power distribution systems are increasingly stressed as they operate closer to their voltage stability limits, driven by growing electricity demand, complex load behaviors, and the evolving structure of power networks. Radial distribution systems, in particular, are highly susceptible to voltage instability under critical loading conditions, where even minor load increases can trigger voltage collapse. Such events threaten the continuity and quality of power supply and can cause damage to infrastructure and sensitive equipment. While large-scale cascading failures are typically associated with transmission systems, localized cascading effects such as sequential voltage drops, feeder outages, and protective device operations can still occur in distribution networks, especially under high loading. Therefore, reliable and timely voltage stability assessment is essential to maintain system reliability and prevent disruptions. This study presents a comprehensive comparative analysis of four voltage stability indices designed for radial distribution networks. The performance of these indices is evaluated on the IEEE 33-bus and 69-bus test systems under various critical loading conditions and multiple static load models, including Constant Power Load (CPL), Constant Current Load (CIL), Constant Impedance Load (CZL), Composite Load (COML), and Exponential Load (EXL). The analysis investigates each index’s effectiveness in identifying voltage collapse points, estimating critical load levels, and calculating load margins, while also evaluating their robustness across diverse operating scenarios. The findings offer practical insights and serve as a valuable benchmark for selecting suitable voltage stability indicators to support monitoring and planning in modern distribution networks.

1. Introduction

The radial power distribution networks are increasingly facing challenges related to voltage degradation, primarily due to the continuous rise in energy demand and the growing complexity of network operations. Consequently, the identification of buses vulnerable to voltage collapse has attracted significant research attention. The unpredictable and continuous growth in load demand poses a major challenge for radial systems, as fluctuations in load levels can occur at any time and vary by location within the network. During peak demand periods, even slight changes in load can compromise network stability. Therefore, it is essential to detect all potential conditions that may lead to instability before implementing any corrective actions to ensure the secure and reliable operation of the power system.

Voltage stability refers to the ability of a power system to maintain steady-state voltages at all buses within acceptable limits under normal conditions and following disturbances, without leading to progressive voltage decline or system collapse. The ability to accurately predict, in advance, the vulnerable regions of the system where buses are approaching voltage instability is vital for risk mitigation and maintaining overall system reliability. Among the primary causes of voltage instability and collapse is excessive system loading [1,2].

Voltage instability occurs when the load at certain buses reaches or exceeds its maximum allowable level, at which point the power flow solution fails to converge, indicating the onset of voltage collapse [1]. However, near the point of instability, divergence in power flow solutions may also stem from numerical inaccuracies, which can obscure the true stability limits. To address this challenge, researchers have focused on developing reliable techniques for real-time system monitoring, aiming to implement preventive measures before voltage collapse occurs.

For instance, the study presented in [3] applies the Continuation Power Flow (CPF) method to analyze system behavior under gradually increasing load and to determine voltage stability boundaries. Several other voltage stability assessment methods based on power flow analysis have been proposed in earlier works [4,5,6,7,8,9]. In addition, studies such as [10,11,12,13,14] have introduced Jacobian-based techniques for evaluating voltage stability. While these methods offer valuable insights, they are often computationally intensive, mathematically complex, and susceptible to matrix singularity, especially in radial distribution networks. Research in [15,16] employed PQ and PV curve analysis to estimate the stability margin of various buses, identifying the weakest ones as those with the smallest margins. However, these techniques are also relatively complicated and time-consuming. Furthermore, studies in [17,18,19] investigated the use of phasor measurement units (PMUs) for real-time voltage stability assessment. Despite their advantages, PMU-based approaches remain economically unfeasible for widespread deployment in distribution systems.

Studies [20,21,22,23] have investigated the application of Flexible AC Transmission Systems (FACTS) in both transmission and distribution networks to improve system stability and operational performance. In [24,25], the Line Stability Indicator (L_mn) and the Fast Voltage Stability Indicator (FVSI) were introduced for contingency ranking. However, these indices often overlook the influence of active power flow, which can lead to inaccurate identification of voltage collapse in certain scenarios. In contrast, the works in [26,27] estimated voltage stability using the Line Collapse Proximity Indicator (LCPI) and the Line Voltage Stability Indicator (LVSI), both derived from the π-model of transmission lines. Despite these contributions, the overall effectiveness of these indices remains limited, as demonstrated in the comparative analysis presented in [28]. The authors in [29] and [30] introduced the Line Stability Factor (LQP) and the New Voltage Stability Index (NVSI) to assess voltage stability in power systems. However, a key limitation of these indices is their complete omission of branch resistance, which is typically significant in radial distribution networks. This oversight may reduce the accuracy of stability assessments in such systems.

Several previous studies have focused on improving voltage stability assessment by formulating different indices. For example, the authors of [31] developed an index aimed at optimizing the sizing and placement of distributed generation (DG) units to reduce power losses. Although this approach enhances network efficiency, it does not consider voltage angle variations, which are essential for accurately assessing system stability margins. Similarly, the studies presented in [32,33,34] introduced voltage stability indices for radial distribution systems, but these formulations also neglect the effect of voltage angle differences. Such simplifications can lead to inaccurate estimations of the system’s proximity to voltage collapse, especially under heavily loaded under different load models.

Many existing indices also fail to incorporate critical system parameters, including line resistance and voltage angle differences. These parameters play an important role in accurately predicting voltage collapse. For instance, the index proposed in [33] produces values significantly below unity even under normal operating conditions. This behavior may result in misleading conclusions about system stability. In [35], an energy-based voltage stability index was presented. However, its reliance on energy loss calculations introduces additional complexity without necessarily improving diagnostic accuracy.

A more recent study, the Novel Distribution Voltage Stability Index (NDVSI) presented in [36], demonstrated effective application for both stability assessment and the optimal siting and sizing of DG units. Despite these contributions, the study did not evaluate the behavior of the index under varying load models or different power factor conditions, which are common in practical distribution networks.

Furthermore, most studies on voltage stability indices focus primarily on variations in either active or reactive power. They often overlook the complexity of real-world loads and the different models used to represent them. In practical systems, loads consist of both real and reactive power components, which may fluctuate due to continuous changes in demand and power factor. These characteristics highlight the need for more comprehensive and accurate indices that capture all aspects of system behavior.

To address these limitations, the present work provides a comparative study of several widely recognized voltage stability indices applied to radial distribution networks. The aim is to identify a more effective index for assessing system stability under varying load levels and diverse load models. The key contributions of this paper are summarized as follows:

• Comprehensive Evaluation of Stability Indices under Critical Loading Conditions: This study presents an extensive assessment of multiple voltage stability indices in radial distribution systems, examining their effectiveness for monitoring system stability across a wide range of critical loading conditions. These scenarios include elevated active, reactive, and apparent power demands. The proposed framework successfully identifies weak or critical buses and accurately predicts voltage instability as the system approaches its operational limits.
• Incorporation of Diverse Load Models for Realistic Stability Assessment: The methodology integrates a variety of load models, including Constant Power Load (CPL), Constant Current Load (CIL), Constant Impedance Load (CZL), Composite Load (COML), and Exponential Load (EXL). This comprehensive approach ensures a realistic, representative analysis, enhancing the robustness of stability evaluations by testing index performance across different operating conditions.
• Early Detection of Critical System States and Collapse Risk: The proposed approach employs four key voltage stability indices, including the Novel Distribution Voltage Stability Index (NDVSI), to enable timely identification of voltage collapse risks, critical loading points, and vulnerable buses. NDVSI is particularly effective because it captures variations in load and both voltage magnitude and angle, enabling a more precise estimate of proximity to voltage instability than conventional indices. This improved accuracy provides system operators with actionable information, enabling corrective measures to be implemented before instability occurs. In addition, the method calculates the available loading margin in megavolt-amperes (MVA) for each load model, further assisting operators in implementing preventive strategies and maintaining reliable system operation.
• Benchmarking and Comparative Analysis of Stability Indices: A detailed comparative study is conducted to assess the effectiveness, sensitivity, and diagnostic accuracy of the evaluated stability indices. The findings highlight the most reliable and efficient index for voltage stability monitoring, providing valuable guidance for operational decisions and future research directions.

The remainder of this article is organized as follows. Section 2 presents the methodology for assessing voltage stability in radial distribution networks. Section 3 describes the case studies and discusses the simulation results. Finally, Section 4 concludes the paper with key findings and insights.

2. Assessment Methodology for Voltage Stability in Radial Power Distribution Networks

2.1. Voltage Stability Indices

This section details a structured method for analyzing voltage stability in radial distribution systems using specific stability indices. It begins by reviewing the most widely recognized indices reported in the literature, highlighting their principles and limitations. The study compares these indices in terms of collapse-prediction accuracy across different operating scenarios for radial power distribution systems. Furthermore, this section details the power flow techniques utilized in the assessment process, establishing a robust analytical framework for identifying critical operating conditions and improving the accuracy of voltage stability assessment in distribution systems.

Table 1. Comparison of voltage stability indices for radial distribution system.

Index	Equation	Critical Value	Assumptions	Ref.
SI [32]	$SI=V_s^4-4{(P_{r}X-Q_{r}R)}^2-4V_s^2(P_{r}R+Q_{r}X)$	0.00	δ = 0 and Y = 0	[32]
SI [33]	$SI=0.5V_r^2-P_{r}R-Q_{r}X$	0.00	δ = 0 and Y = 0	[33]
SI [34]	$SI=2V_s^2{V}_r^2-V_r^4-2V_r^2(P_{r}R+Q_{r}X)-Z^2(P_r^2+Q_r^2)$	0.00	δ = 0 and Y = 0	[34]
NDVSI [36]	$NDVSI=V_s^2{\sin }^2(\theta -\delta +{45}^{\circ })-2\sqrt{2}Z(P_r+Q_r)\sin (\theta +{45}^{\circ })$	0.00	Y = 0	[36]

summarizes the well-known indices, including the recently published Novel Distribution Voltage Stability Index (NDVSI [36]), highlighting their key characteristics and underlying assumptions. It is important to observe that the indices (SI [32], SI [33], and SI [34]) disregard the impact of voltage angle differences and the shunt admittance of distribution lines, which can limit their accuracy under certain operating conditions. In contrast, the NDVSI incorporates all line parameters, such as resistance, reactance, and voltage angle difference, providing a more comprehensive and realistic evaluation of system stability. NDVSI also considers the magnitude of receiving active and reactive power load ($\left|P_r\right| \mathrm{a}\mathrm{n}\mathrm{d} \left|Q_r\right|$). The only exception is the line shunt admittance, which is typically negligible in radial power networks and therefore has no effect on voltage stability assessment.

The selection of these indices was guided by their extensive recognition in prior research, high citation impact, and consistent application in evaluating voltage stability. Although the indices [32,33,34] share the same abbreviation “SI,” they originate from separate studies conducted by different authors. Each index is based on a distinct mathematical formulation and analytical approach, resulting in significant differences in performance and interpretation. To maintain clarity and eliminate any potential confusion, each index is distinctly labeled with its corresponding citation: SI [32], SI [33], and SI [34]. These indices originate from separate formulations of the power flow equations, which lead to differences in how they react to various system operating conditions. For example, under normal load levels, SI [33] generally yields a value near 0.5, whereas SI [32], SI [34], and the NDVSI [36] tend to produce values approaching 1, suggesting a strong voltage stability margin. This behavior supports the conventional view that lower index values nearing zero signify a higher likelihood of voltage collapse. When the system is subjected to heavier loads in terms of active, reactive, or apparent power, the indices respond differently in identifying stressed states. These patterns are thoroughly examined in the section dedicated to case studies.

The critical value for all the voltage stability indices considered in this study is zero, as shown in Table 1. Ideally, the value of each index should approach this critical threshold as the system load nears its maximum permissible level, indicating an increased risk of voltage collapse. Higher index values correspond to a safer operating state, while values approaching zero signal that the system is at risk of collapse. Each index exhibits distinct behavior due to differences in its derivation and underlying assumptions. For instance, SI [32], SI [34], and the NDVSI [36] have values close to 1.00 under low or normal loading conditions, reflecting a high stability margin. In contrast, SI [33] shows a value near 0.5 under base case loading.

As the system load increases, SI [32], SI [34], and the proposed NDVSI [36] gradually decrease from 1.00 toward zero, while SI [33] decreases from 0.5 toward zero. This trend demonstrates that all indices are expected to approach zero as the system approaches critical loading conditions. At or near critical loads, an index value closer to zero provides a more accurate representation of voltage collapse risk, offering a precise early warning. Conversely, indices that remain significantly above zero under such conditions may give misleading results, suggesting that the system remains stable when it is, in fact, at risk of collapse.

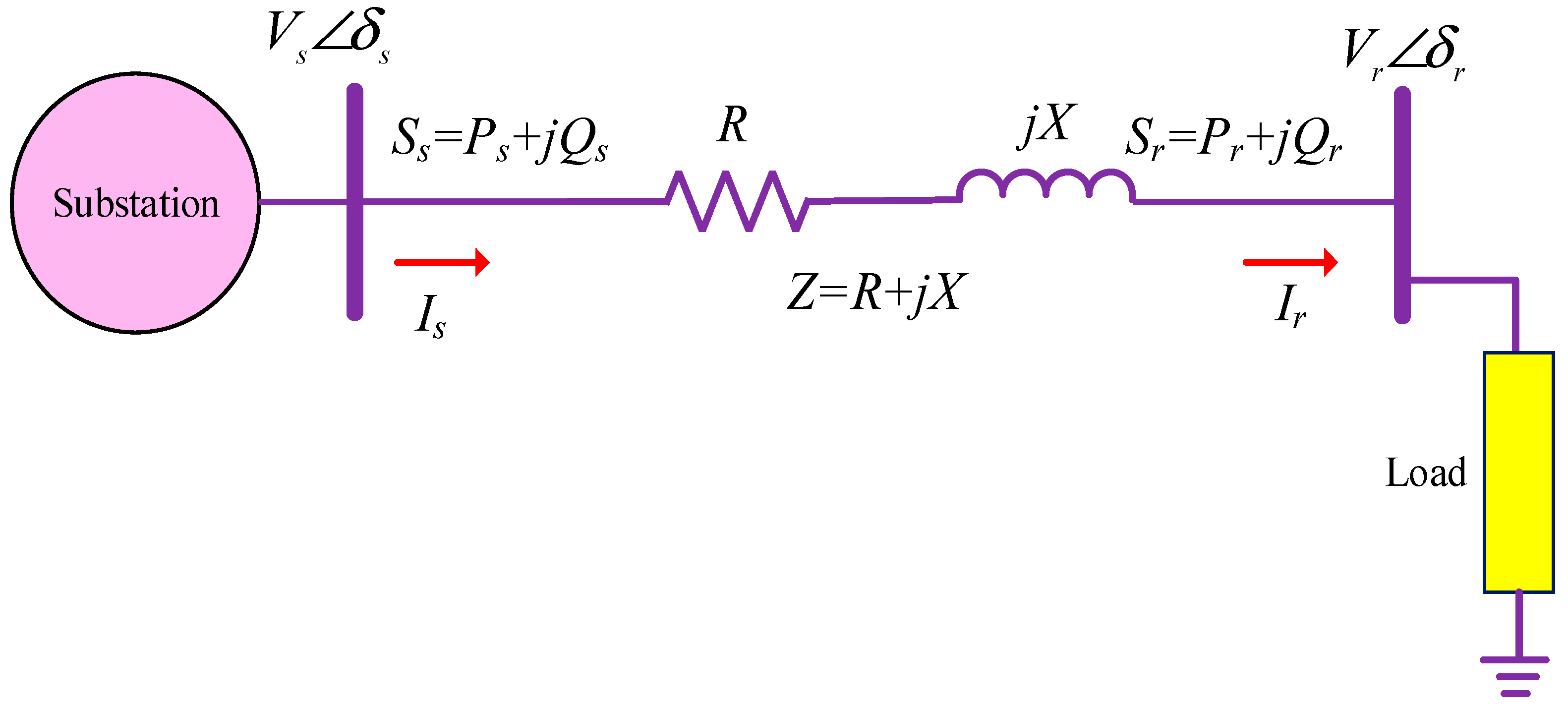
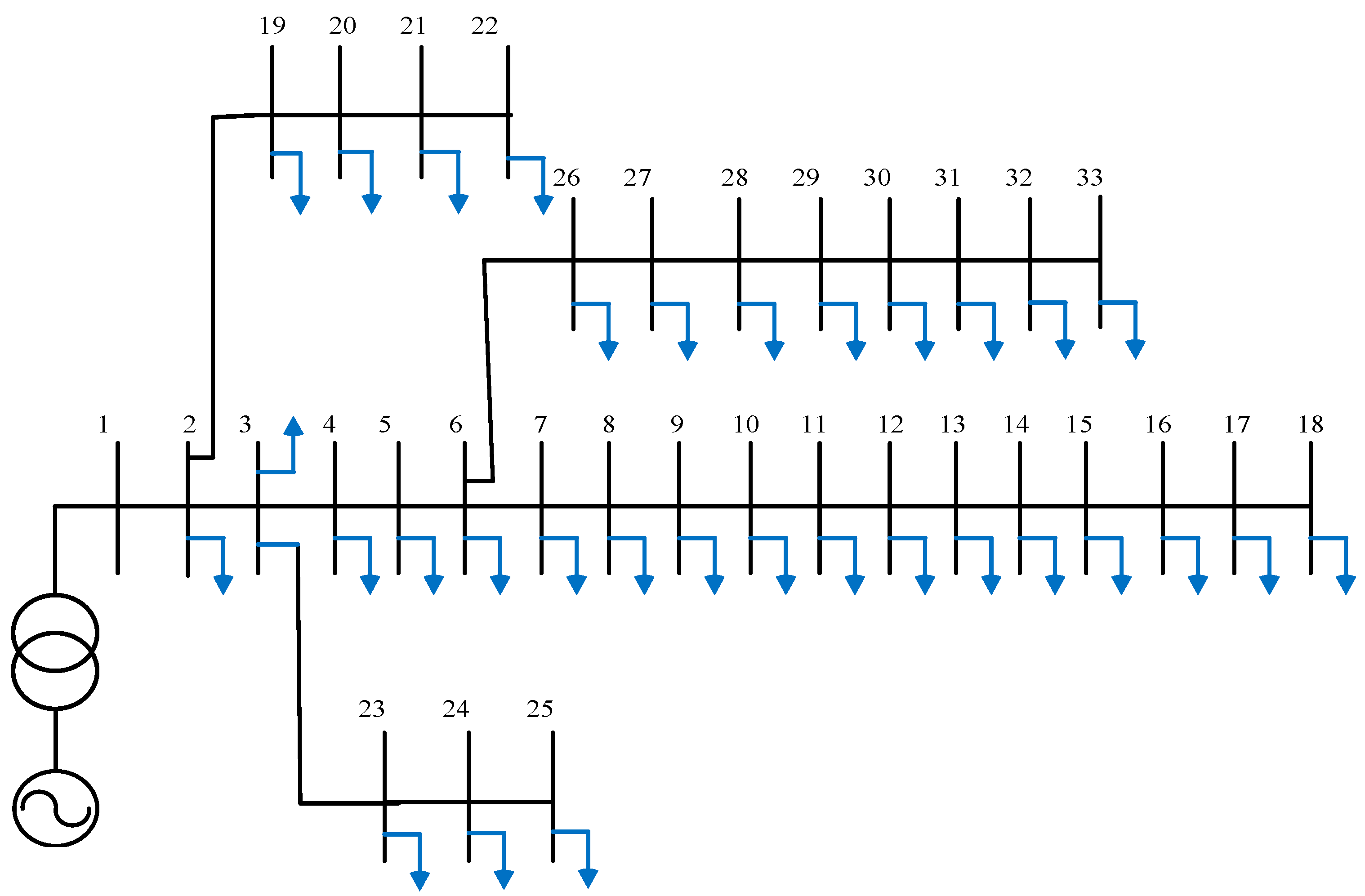
The single-line representation of a radial distribution network (RDN) is presented in Figure 1, with the substation located at bus-s and the load placed at bus-r. Because the $\sin (\theta +{45}^{\circ })=\cos (\theta -{45}^{\circ })$, the Novel Distribution Voltage Stability Index (NDVSI [36]) can also be rewritten as:

$$NDVSI=V_s^2{\cos }^2(\theta -\delta -{45}^{\circ })-2\sqrt{2}Z(P_r+Q_r)\cos (\theta -{45}^{\circ })$$

(1)

In a stable operating condition with normal loading, the NDVSI maintains values above zero close to 1. However, under instability scenarios like critical loading, the index decreases and eventually reaches zero. Values approaching zero indicate that the system is at a higher risk of voltage collapse.

From Equation (1), NDVSI [36] values are not solely dependent on the voltage magnitude. This is because NDVSI is derived from the quadratic voltage equation, which itself is obtained from the power flow through the line of a two-bus equivalent system, where it relates the real ($P_r$) and reactive ($Q_r$) powers projected along the line impedance angle ($\theta$). The term $\mathrm{c}\mathrm{o}\mathrm{s}(\theta -\delta -{45}^{\circ })$ reflects the phase alignment between the line impedance and the bus voltage angles. The first term, $V_s^2{\mathrm{c}\mathrm{o}\mathrm{s}}^2(\theta -\delta -{45}^{\circ })$, represents the stabilizing effect of the sending-end voltage—higher sending voltage or smaller phase deviation enhances the voltage stability at the receiving end. Conversely, the second term, $2\sqrt{2}Z\left(P_r+Q_r\right)\cos \left(\theta -{45}^{\circ }\right),$ represents the destabilizing effect of power transfer through the line impedance. The NDVSI value decreases as the load ($P_r$ and $Q_r$) increases or when the impedance angle ($\theta$) becomes large, indicating a reduced voltage stability margin.

Unlike NDVSI, conventional indices neglect the influence of voltage-angle differences and are unrelated to the impedance angle, as illustrated in Table 1. Therefore, each index exhibits distinct characteristics due to the distinct assumptions made during its formulation.

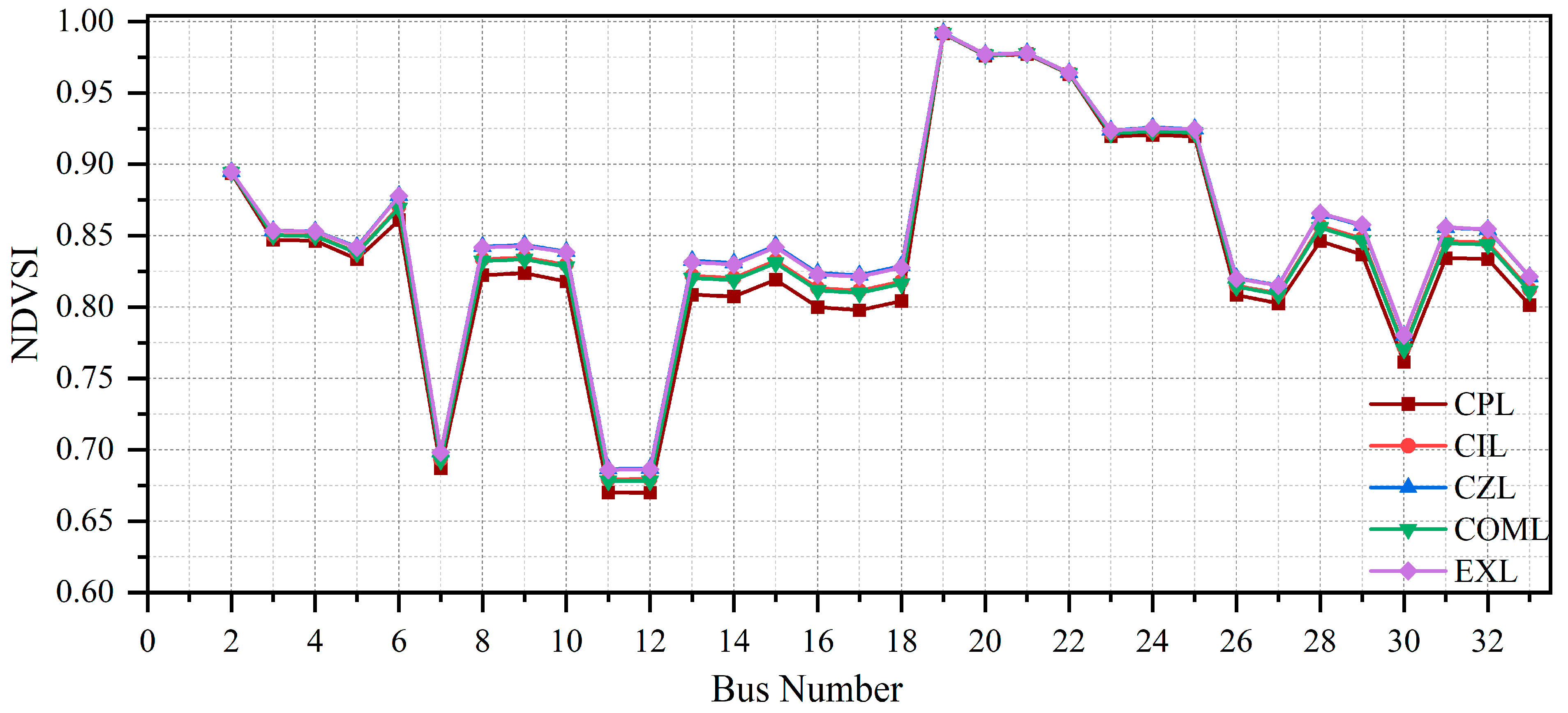
In summary, NDVSI captures the combined influence of sending-end voltage magnitude, load power, line impedance, and phase angle, not voltage alone. This explains the nonlinear relationship observed between NDVSI and bus voltages. Consequently, NDVSI does not necessarily follow the voltage profile monotonically; instead, it reflects the system’s voltage stability sensitivity rather than absolute voltage magnitudes.

2.2. The Power Flow Solution

While methods such as Newton-Raphson, Gauss-Seidel, and Fast Decoupled are commonly employed for power flow analysis, they can become less effective when applied to radial distribution networks. This is because of the high ratios of R/X and the special structures of distribution grids. Consequently, this study obtains the power flow solutions by utilizing two matrices [37,38]: the Bus-Injection-to-Branch-Current (BIBC) matrix and the Branch-Current-to-Bus-Voltage (BCBV) matrix.

2.2.1. The Bus-Injection-to-Branch-Current Matrix (BIBC)

For distribution systems, the current injection–based modeling approach, as described in [38], is particularly suitable for the applied power flow analysis method. At each bus $i$, the complex power injection is represented as $S_i=P_i+j{Q}_i$, where $i=1,2,3,\dots ,N$. Accordingly, the equivalent current injection corresponding to the $k$-th iteration of the solution can be expressed as:

$$I_i^k=I_i^r(V_i^k)+j{I}_i^i(V_i^k)={\left({\displaystyle \frac{P_i+j{Q}_i}{V_i^k}}\right)}^{\ast }$$

(2)

Here, $V_i^k$ denotes the voltage at the node during the Kth iteration, while $I_i^k$ indicates the equivalent current injection at the same iteration. This current consists of real and imaginary components, represented by $I_i^r$ and $I_i^i$, respectively. The conjugate (*) is used because in power systems, the current injected into a bus is related to the conjugate of the complex power divided by voltage, i.e., $I_i={\left({\displaystyle \frac{S_i}{V_i}}\right)}^{*}$.

As shown in Figure 2, a simplified radial distribution network is considered as an illustrative case. Kirchhoff’s Current Law (KCL) is applied by formulating equations that convert nodal power injections into their equivalent current injections. Consequently, the branch currents can be expressed based on the equivalent current injections. For example, the currents in branches B5, B3, and B1 can be represented as follows:

$$B_5=I_6$$

(3)

$$B_3=I_4+I_5$$

(4)

$$B_1=I_2+I_3+I_4+I_5+I_6$$

(5)

Furthermore, BIBC matrix can be constructed as follows:

$$\left[\begin{array}{l}{B}_1\\ B_2\\ B_3\\ B_4\\ B_5\end{array}\right]=\left[\begin{array}{ccccc}1& 1& 1& 1& 1\\ 0& 1& 1& 1& 1\\ 0& 0& 1& 1& 0\\ 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]\left[\begin{array}{l}{I}_2\\ I_3\\ I_4\\ I_5\\ I_6\end{array}\right]$$

(6)

In general, Equation (6) can be written as

$$\left[B\right]=\left[BIBC\right]\left[I\right]$$

(7)

The following steps summarize the algorithm used to generate the symmetric upper triangular matrix BIBC:

• For a distribution system comprising m branch sections and n buses, the BIBC matrix has dimensions of m × (n − 1).
• If a line section (B_k) connects bus i to bus j, the BIBC matrix is updated by copying the column corresponding to bus i into the column for bus j, and then placing a + 1 in the kth row and jth column.
• Continue applying Step 2 until all line sections are incorporated into the BIBC matrix. The construction of this process is illustrated in Figure 3.

2.2.2. Branch-Current-to-Bus-Voltage Matrix (BCBV)

Figure 2 shows how the impedance matrix helps define the connection between branch currents and bus voltages. As an example, the voltages at buses 2, 3, and 4 can be written as:

$$V_2=V_1-B_1{Z}_{12}$$

(8)

$$V_3=V_2-B_2{Z}_{23}$$

(9)

$$V_4=V_3-B_3{Z}_{34}$$

(10)

Z_ij denotes the impedance of the branch that links bus-i to bus-j. V_i represents the voltage at bus-i. Upon substituting Equations (8) and (9) into (10), the voltage at bus 4 is given by:

$$V_4=V_1-B_1{Z}_{12}-B_2{Z}_{23}-B_3{Z}_{34}$$

(11)

It is clear from (11) that the substation voltage, branch-current, and line-impedance can all be used to represent the bus voltage. The same procedure can be applied to the other buses, yielding the BCBV matrix, which is expressed as:

$$\left[\begin{array}{l}{V}_1\\ V_2\\ V_3\\ V_4\\ V_5\end{array}\right]-\left[\begin{array}{l}{V}_2\\ V_3\\ V_4\\ V_5\\ V_6\end{array}\right]=\left[\begin{array}{ccccc}{Z}_{12}& 0& 0& 0& 0\\ Z_{12}& Z_{23}& 0& 0& 0\\ Z_{12}& Z_{23}& Z_{34}& 0& 0\\ Z_{12}& Z_{23}& Z_{34}& Z_{45}& 0\\ Z_{12}& Z_{23}& 0& 0& Z_{36}\end{array}\right]\left[\begin{array}{l}{B}_1\\ B_2\\ B_3\\ B_4\\ B_5\end{array}\right]$$

(12)

Equation (12) can be reformulated in a general expression as:

$$\left[\Delta V\right]=\left[BCBV\right]\left[B\right]$$

(13)

An algorithm for building the BCBV matrix can be designed in the following manner, relying on (13):

• In a distribution network consisting of n buses and m branch sections, the BCBV matrix is structured with dimensions of (n − 1) × m.
• When a line section (B_k) connects Bus-i and Bus-j, the impedance of that line (Z_ij) is inserted into the kth column of the row corresponding to Bus-j in the BCBV matrix. Additionally, the row associated with Bus-i is duplicated and assigned to Bus-j to reflect the connectivity.
• Proceed with Step 2 again until the BCBV matrix contains all of the line sections. Figure 4 illustrates Building Process (2) for the BCBV matrix.

2.2.3. Power Flow Solution Technique

The formulation of the BIBC and BCBV matrices is fundamentally based on the topology of distribution networks. By integrating Equations (13) and (7), a comprehensive relationship is established between bus voltage profiles and current injections within the system.

$$\Delta V=\left[BCBV\right]\left[BIBC\right]\left[I\right]=\left[DLF\right]\left[I\right]$$

(14)

Iteratively solving Equation (15a,b) yields the distribution load flow solution:

$$I_i^k=I_i^r(V_i^k)+j{I}_i^i(V_i^k)={\left({\displaystyle \frac{P_i+j{Q}_i}{V_i^k}}\right)}^{\ast }$$

(15a)

$$\left[\Delta V^{k+1}\right]=\left[DLF\right]\left[I^k\right]$$

(15b)

This power flow solution requires less computational effort compared to the Newton–Raphson and Gauss–Seidel methods. Therefore, it is also suitable for online operation [37,38].

2.3. Load Modeling

2.3.1. Formulation of Load Modeling

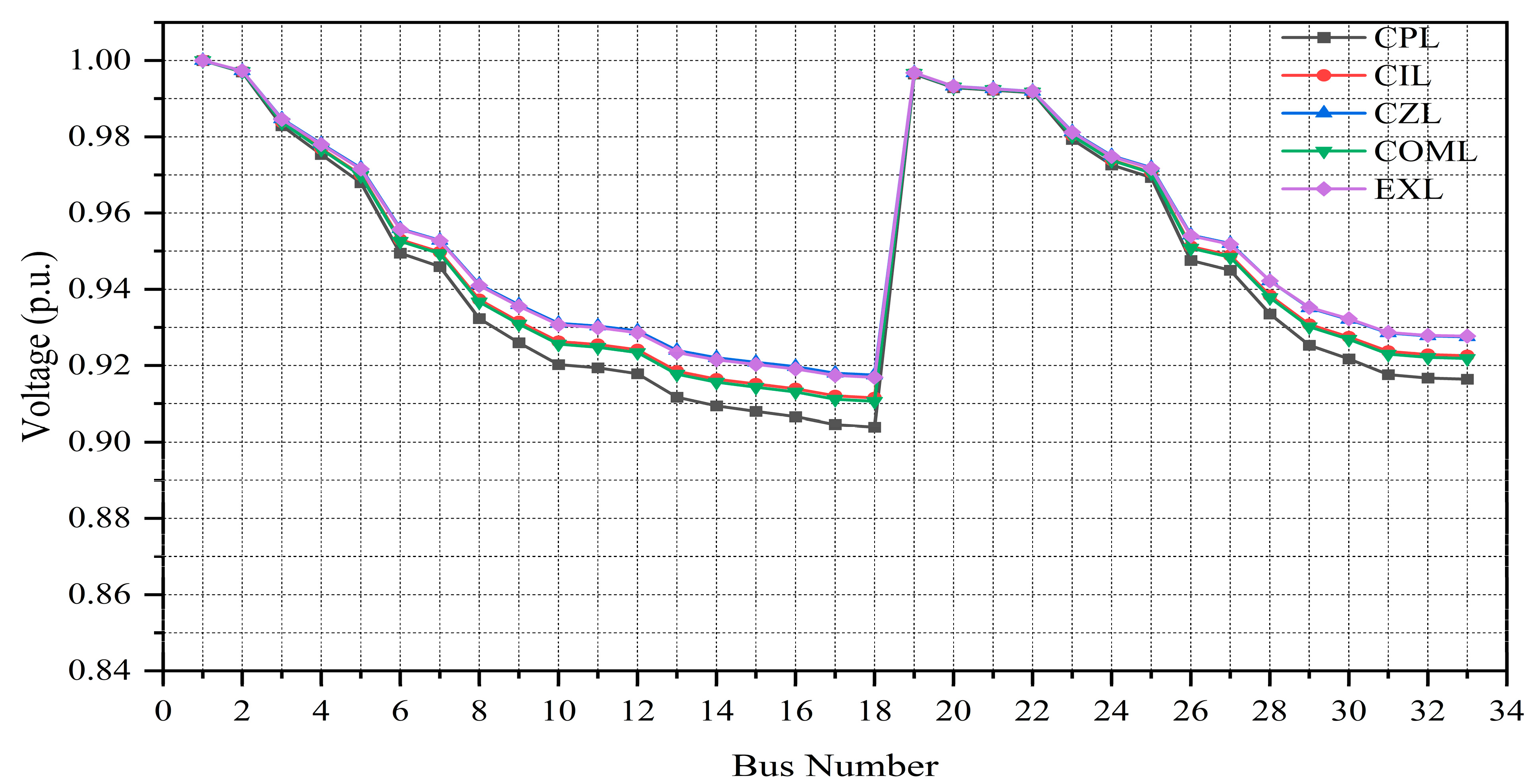
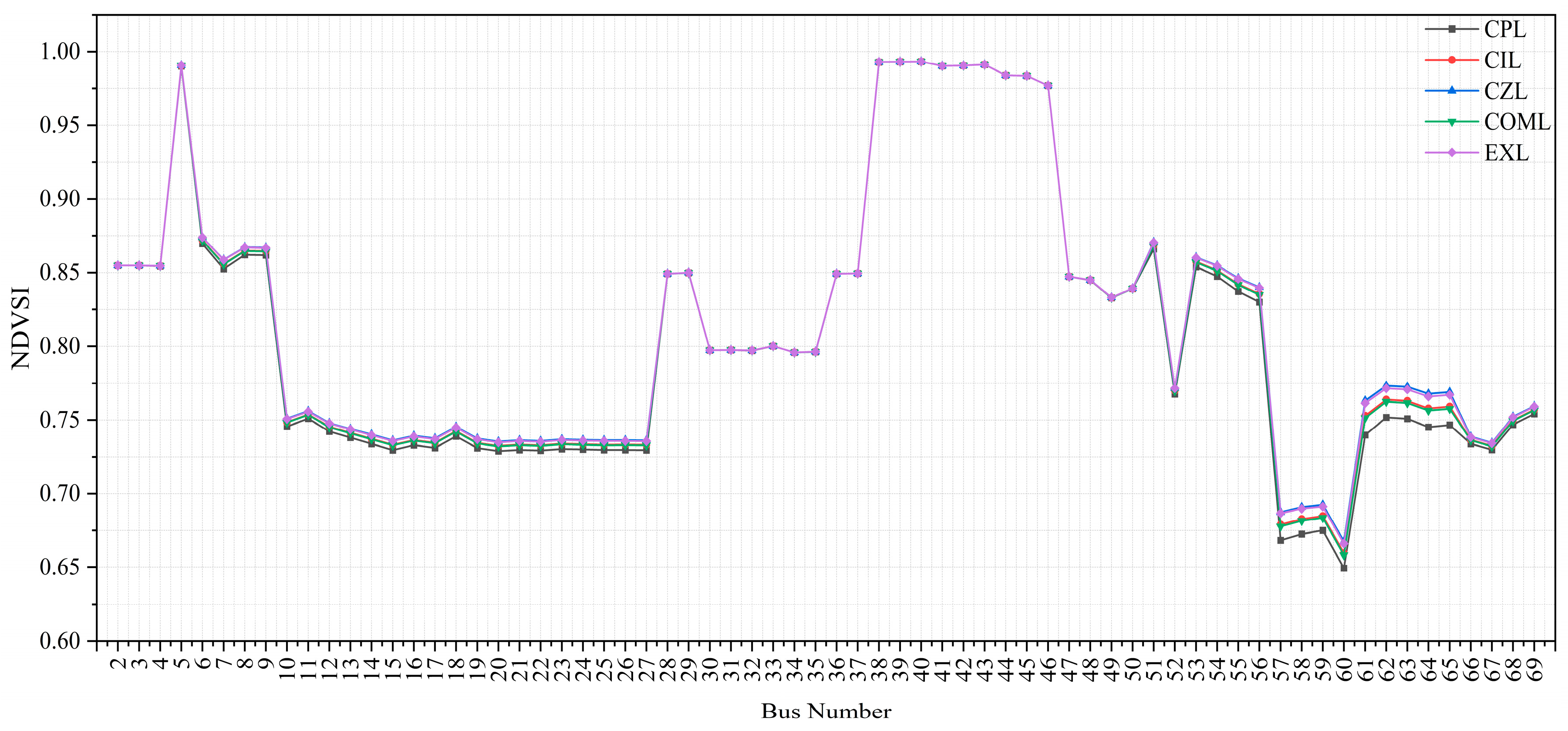
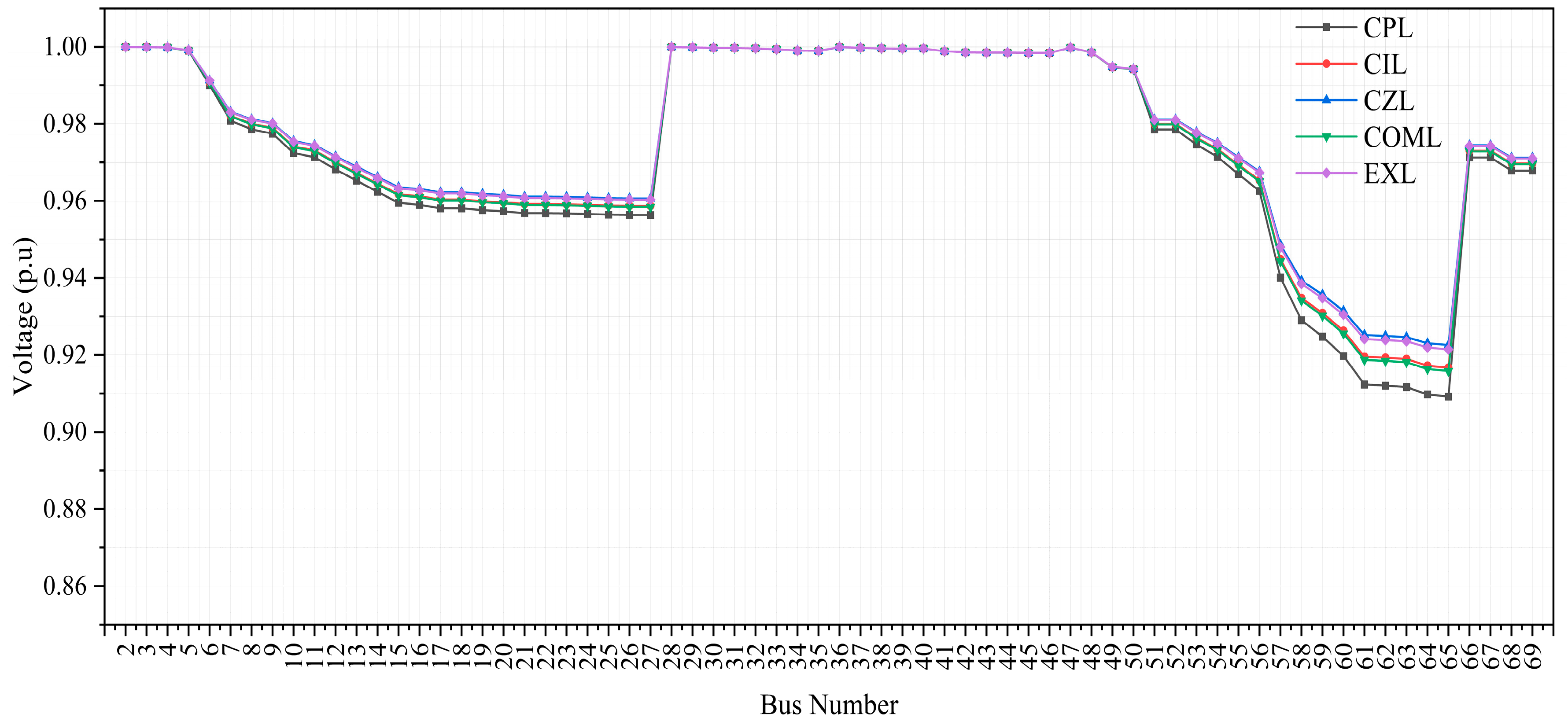
This study examines various balanced power load models, including constant power (CPL), constant current (CIL), constant impedance (CZL), composite (COML), and exponential (EXL). A unified mathematical representation encompassing these load types is provided in Equations (16) and (17).

$$P=P_0({\alpha }_0{V}^0+{\alpha }_1{V}^1+{\alpha }_2{V}^2+{\alpha }_3{V}^{e_1})$$

(16)

$$Q=Q_0({\beta }_0{V}^0+{\beta }_1{V}^1+{\beta }_2{V}^2+{\beta }_3{V}^{e_2})$$

(17)

The nominal active and reactive power are represented by $P_0$ and $Q_0$, respectively. V represents the bus voltage. Equations (16) and (17) have constraints in the following ways for every load:

$${\alpha }_0+{\alpha }_1+{\alpha }_2+{\alpha }_3=1$$

(18)

$${\beta }_0+{\beta }_1+{\beta }_2+{\beta }_3=1$$

(19)

This study assesses the voltage stability of radial distribution systems during the following load models:

(1)

Constant Power Load (CPL)

For this model, ${\alpha }_0={\beta }_0=1$ and ${\alpha }_i={\beta }_i=0$ for $i=1,2,3$. The system was tested under 100% CPL conditions at both base and critical loading levels. In this case, the load power remains constant regardless of voltage variations.

(2)

Constant current load (CIL)

For this model, ${\alpha }_1={\beta }_1=1$ and ${\alpha }_i={\beta }_i=0$ for $i=0,2,3$. The system was tested under 100% CIL conditions at base and critical loading levels. In this case, the load power is linearly proportional to the voltage magnitude.

(3)

Constant impedance load (CZL)

For this model, ${\alpha }_2={\beta }_2=1$ and ${\alpha }_i={\beta }_i=0$ for $i=0,1,3$. The system was tested under 100% CZL conditions at base and critical loading levels. In this case, the load power varies with the square of the voltage magnitude.

(4)

Composite load (COML)

This model consists of 40% CPL, 30% CIL, and 30% CZL (ZIP components). The system was tested at both base and critical loading levels. This composite model allows for a more realistic representation of practical loads that exhibit mixed characteristics of power, current, and impedance components.

(5)

Exponential load (EXL)

For this model, ${\alpha }_3={\beta }_3=1$ and ${\alpha }_i={\beta }_i=0$ for $i=0,1,2$. The exponential exponents e₁ and e₂ are set to 1.38 and 3.22, respectively [38]. The system was tested under 100% EXL conditions at base and critical loading levels.

2.3.2. Explanation and Influence of Load Models on Voltage Stability

(1)

Constant Power Load (CPL)

Description: Power consumption remains unchanged even when the voltage varies.

Impact on Voltage Stability: CPLs tend to reduce voltage stability because they draw the same power even at lower voltages, forcing the system to increase current and resulting in a larger voltage drop. This negative damping effect can lead to voltage collapse under stressed conditions.

(2)

Constant Current Load (CIL)

Description: Power consumption changes linearly with voltage (i.e., $P \mathrm{a}\mathrm{n}\mathrm{d} Q\propto V$).

Impact on Voltage Stability: CILs exhibit moderate sensitivity to voltage changes. They are more stable than CPLs but less stable than CZLs, providing a balance between system stiffness and flexibility.

(3)

Constant Impedance Load (CZL)

Description: Power consumption varies with the square of voltage ($P \mathrm{a}\mathrm{n}\mathrm{d} Q\propto V^2$).

Impact on Voltage Stability: CZLs support voltage stability because their power demand decreases with voltage drop, naturally relieving system stress and preventing collapse.

(4)

Composite Load (COML)

Description: Represents a mixture of CPL, CIL, and CZL components, capturing the realistic behavior of actual loads (e.g., households or industrial systems).

Impact on Voltage Stability: The stability behavior depends on the relative share of each component. A higher CPL portion tends to weaken stability, while a higher CZL portion improves it.

(5)

Exponential Load (EXL)

Description: Power varies with voltage raised to exponents $e_1$ and $e_2$, typically derived from empirical data.

Impact on Voltage Stability: EXL provides greater modeling flexibility, enabling more accurate representation of nonlinear load responses. For $e_1=1.38$ and $e_2=3.22$, the load exhibits nonlinear but generally stabilizing behavior at higher voltages [38].

2.4. Contingency Monitoring and Voltage Stability Assessment During Different Operating Load Conditions

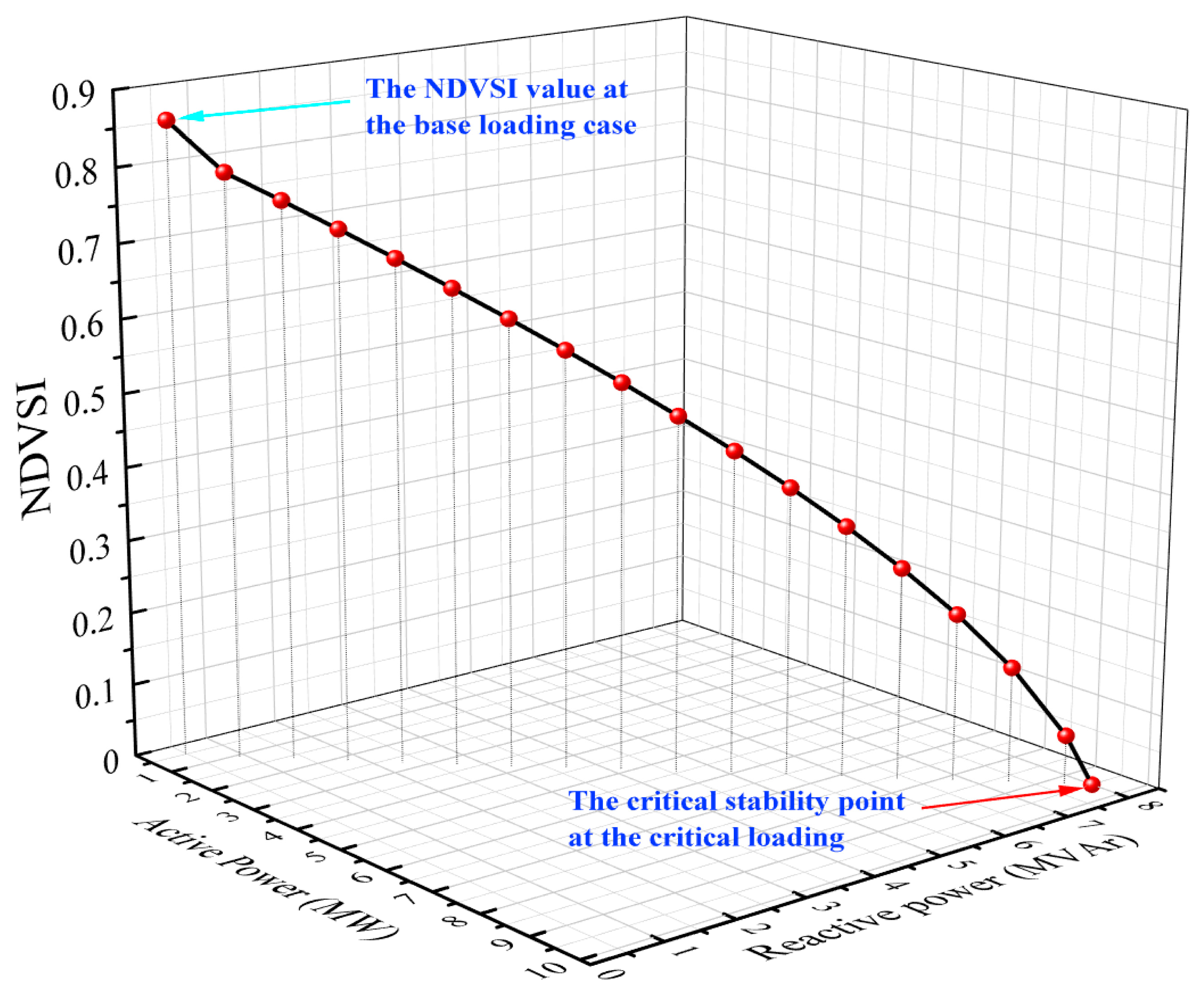
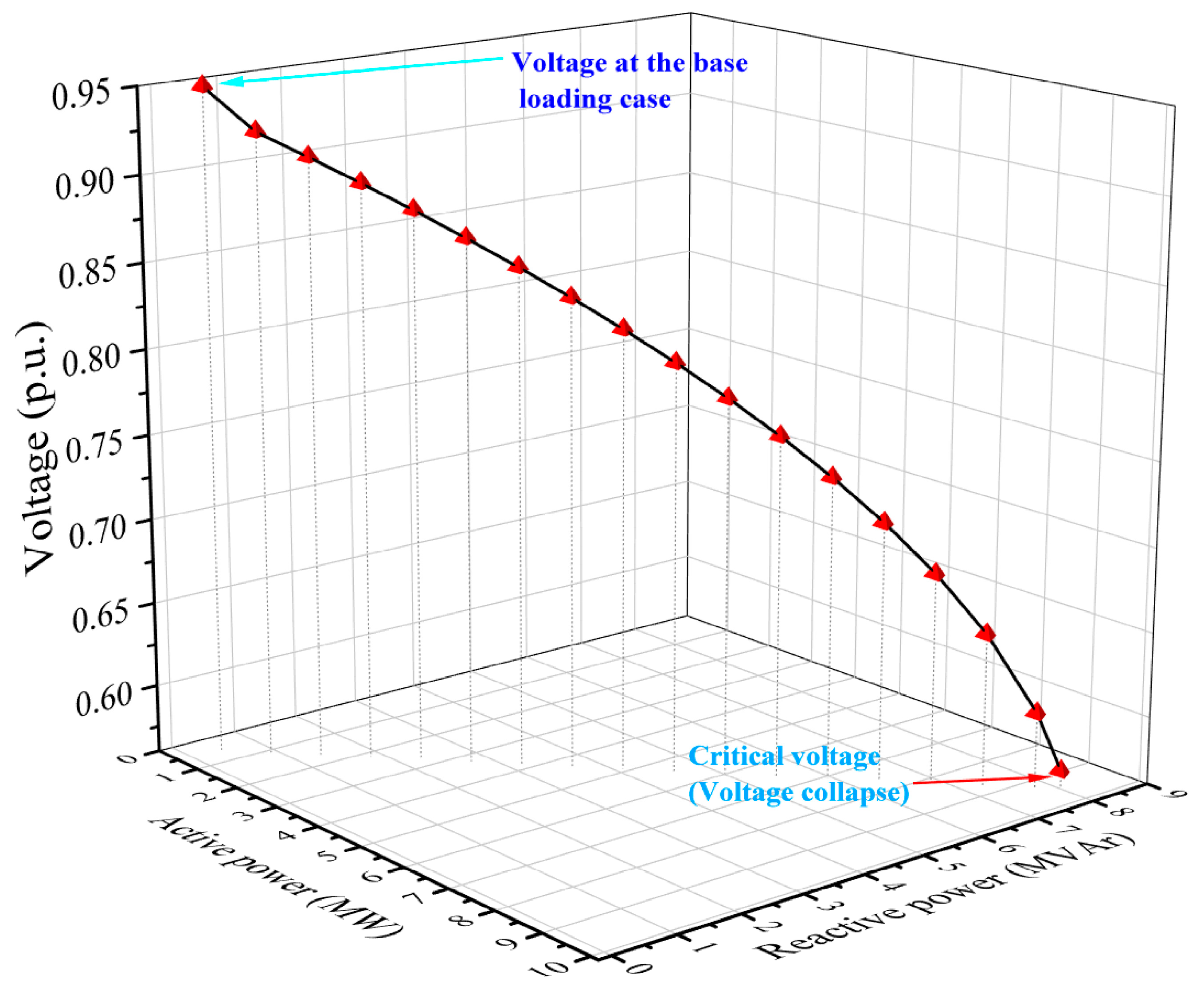
Voltage stability analysis mainly focuses on identifying voltage collapse conditions, determining the highest load the system can handle, recognizing weak buses and branches, and estimating the remaining load margin. Understanding the proximity of the system to voltage collapse points is essential for ensuring continuous power supply. The suggested method for contingency monitoring under various operating load scenarios at various power factors is presented in this paper. In various likely operating load levels, the index’s efficacy in online system stability monitoring is evaluated. Different probable loads are progressively increased until the maximum permitted load is reached in order to assess the practicality of each index in diagnosing the critical nodes. To forecast voltage collapse at this juncture, the index must approach the stability threshold, which is zero. 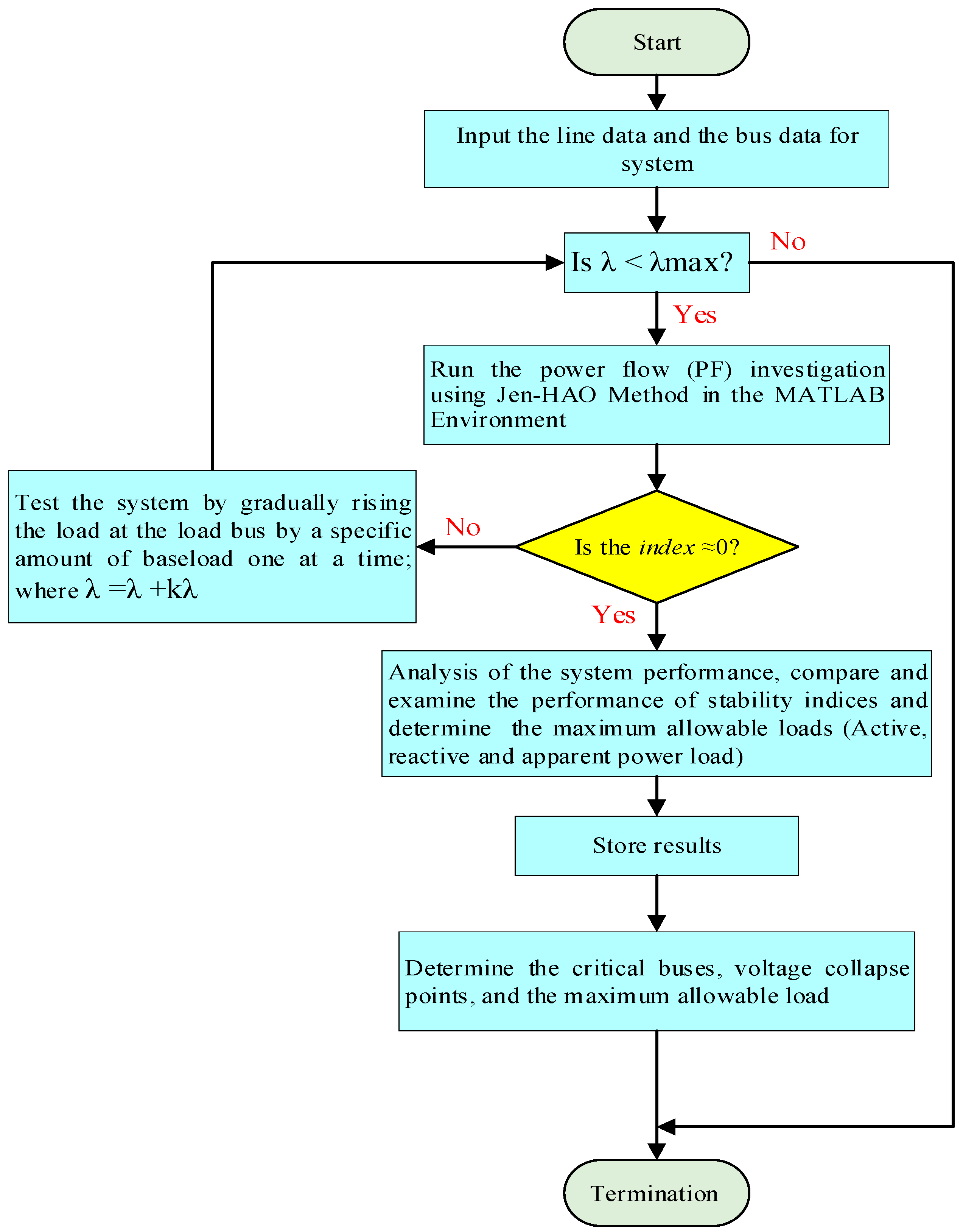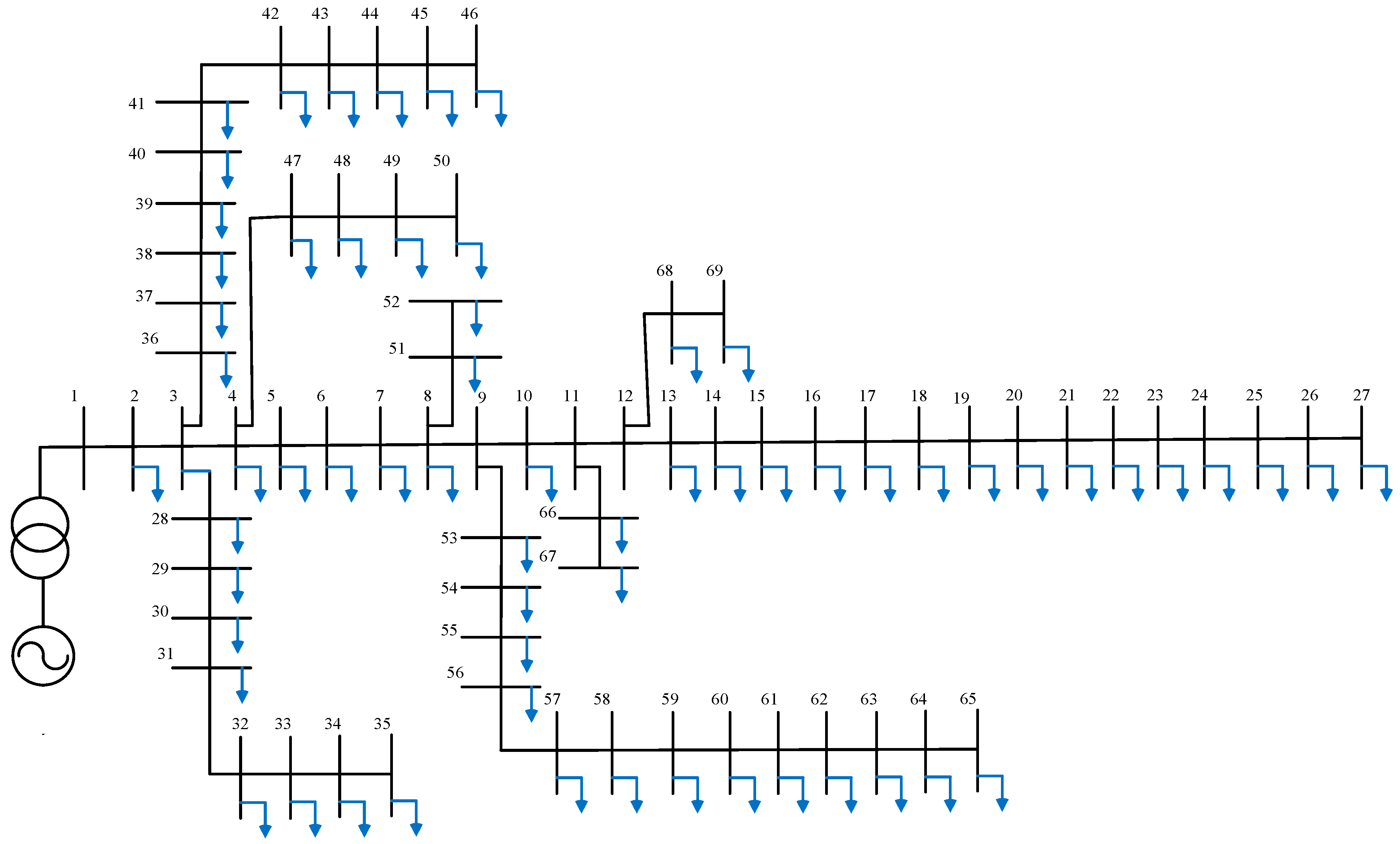Figure 5 represents the procedures for contingency monitoring during different load operations. The evaluation of the indices is carried out on the IEEE 33-bus and IEEE 69-bus systems to assess their effectiveness and practical applicability as follows:

Scenario 1: In this scenario, the distribution system is evaluated under base-case loading conditions to examine the overall stability status of all nodes. Voltage stability indices are calculated to identify both strong and weak locations within the network. Since the system operates under normal conditions, the index values are expected to remain close to unity, signifying a stable operating state and a significant margin from the critical collapse point (index = 0). A node is considered more stable as its index approaches unity, whereas its proximity to zero indicates an increased risk of voltage collapse.

Scenario 2: This scenario evaluates the voltage stability of the distribution system by progressively increasing the load (active, reactive, or apparent power) at a selected node until it reaches its maximum permissible limit. The objective is to validate the capability of each index in identifying critical buses and predicting voltage collapse under stressed operating conditions. As the system loading approaches the critical threshold, the stability index is expected to decrease toward zero, indicating proximity to instability. Figure 5 illustrates the contingency monitoring procedure under various loading scenarios. The following procedure is applied to assess the performance and practical applicability of stability indices using the IEEE 33-bus and IEEE 69-bus test systems.

(1)

Enter the data for the radial power distribution system.

(2)

The Jen-HAO method, utilizing the BIBC and BCBV matrices, is employed to solve the power flow.

(3)

Each index values are calculated during the base loading case to estimate the stability of the system.

(4)

The maximum permissible load at each selected load bus, under different power factor conditions, is determined by gradually increasing the load by k% until the power flow solution diverges or the index value approaches the stability limit (0.0). In Figure 5, λ represents the load under base-case conditions, while λₘₐₓ denotes the maximum allowable loading level. At base-case loading, the index values are close to 1.0, indicating a stable system condition. As the load increases, the index values decrease, and for the most critical bus, the index approaches zero or reaches zero when the load attains its maximum level (λ = λₘₐₓ). Beyond this point, any additional load causes the power flow to diverge, signifying system instability.

(5)

When the load goes above the limit, the solution doesn’t converge. In this instance, the voltage collapse point can be determined by reducing the load by a certain quantity.

(6)

As the load increases, the index gradually decreases from one to zero, reaching the stability limit.

(7)

Determine the buses associated with the smallest stability index values, as these indicate the most critical nodes in the network.

(8)

For alternative likely load scenarios, choose a different load bus and execute steps 1 through 7 again.

(9)

For alternative loading scenarios, a different load bus is selected, and steps 1 through 7 are repeated. Step 4, in particular, offers a systematic approach for determining the maximum loadability of each bus. Even when the system operates near the voltage collapse point, the high-performance index demonstrates strong capability in accurately monitoring and assessing the risk of voltage instability.

(10)

Compare the well-known stability indicators (SI [32], SI [33], SI [34], and NDVSI [36]) and repeat all the procedures mentioned above in multiple cases for verification.

Scenario 3: This scenario evaluates the system’s loading margin (in MVA) by uniformly increasing both active and reactive power across all load buses. The loading process begins from the base level (λ) and increases incrementally according to λ = λ(1 + k) until it reaches the maximum loading point (λ = λₘₐₓ). The procedure follows steps similar to those described in Scenario 2; however, unlike Scenario 2, where the load is increased at a single node, Scenario 3 applies the load increment simultaneously at all load buses. The process continues until the index approaches zero or the power flow solution fails to converge. The loading margin (S_margin) is then computed as the difference between the base-case loading (λ) and the maximum permissible loading (λ = λₘₐₓ), and it is expressed as:

$$S_{\max }={\lambda }_{\max }{S}_{base}$$

(20)

$$S_{\mathrm{margin}}=({\lambda }_{\max }-1)S_{base}$$

(21)

3. Case Studies and Simulation Results

This work presents a comprehensive evaluation and comparison of four stability indices mentioned above on the IEEE 33-bus and IEEE 69-bus systems across multiple operating scenarios to investigate their feasibility and performance. The values of these indices are near one for no-load cases, and they reduce to zero during heavy-loading cases.

3.1. IEEE 33-Bus Test System During Base Loading Condition

This section presents an assessment of the voltage stability condition for the IEEE 33-bus radial power distribution system, utilizing four voltage stability indices under the base load scenario. Figure 6 depicts the line diagram of the IEEE 33-bus test system. The voltage stability indices are employed to evaluate the system’s voltage stability performance under different load models, namely CPL, CZL, CIL, COML, and EXL, as summarized in

Table 2. Stability Indices for the IEEE 33-Bus Test System at Base Case Loading Conditions.

ToL	Bus	NDVSI [36]	SI [32]	SI [33]	SI [34]
CPL	4	0.8464	0.9048	0.4683	0.9190
	9	0.8238	0.7350	0.4228	0.7452
	19	0.9914	0.9861	0.4960	0.9871
	27	0.8027	0.7974	0.4441	0.8018
	32	0.8337	0.7061	0.4193	0.7075
CIL	4	0.8501	0.9106	0.4704	0.9238
	9	0.8347	0.7527	0.4284	0.7621
	19	0.9918	0.9867	0.4961	0.9878
	27	0.8097	0.8106	0.4479	0.8147
	32	0.8451	0.7253	0.4251	0.7266
CZL	4	0.8532	0.9154	0.4720	0.9278
	9	0.8435	0.7670	0.4329	0.7759
	19	0.9920	0.9872	0.4963	0.9883
	27	0.8153	0.8213	0.4510	0.8252
	32	0.8543	0.7409	0.4297	0.7422
COML	4	0.8497	0.9100	0.4701	0.9233
	9	0.8335	0.7506	0.4278	0.7602
	19	0.9917	0.9866	0.4961	0.9877
	27	0.8089	0.8091	0.4475	0.8132
	32	0.8438	0.7231	0.4244	0.7244
EXL	4	0.8529	0.9147	0.4718	0.9272
	9	0.8428	0.7659	0.4325	0.7749
	19	0.9920	0.9872	0.4963	0.9882
	27	0.8151	0.8207	0.4509	0.8245
	32	0.8546	0.7414	0.4298	0.7426

. In Table 2, ToL represents the type of load model. In the base case, the load is modeled as CPL, and the corresponding stability assessment is performed. The same procedure is then applied individually to each load model to analyze the system’s voltage stability under various loading scenarios. Due to space constraints, only a representative subset of the results is presented in Table 2, while the remaining NDVSI results are illustrated in Figure 7. Since the NDVSI accounts for all key parameters of distribution systems, it provides more accurate and comprehensive assessments. Under base-load conditions, the NDVSI values remain considerably distant from the critical stability limit (zero), consistent with other stability indices, none of which approach zero under these conditions. Therefore, it can be concluded that the system operates in a stable state at the base load condition.

Notably, the system exhibits higher voltage stability when the load model is represented by the Constant Impedance Load (CZL) compared to the other considered load types. The relative order of stability strength can be expressed as CZL > EXL > CIL > COML > CPL. The recently developed index, NDVSI [36], is employed to examine its sensitivity to variations in load models, as it provides more accurate and reliable results compared to conventional indices. Figure 7 presents the variations in NDVSI values under different load models, whereas Figure 8 illustrates the corresponding voltage profiles influenced by these load model effects.

Figure 7 illustrates that the NDVSI for the lateral spanning nodes 6–18 exhibits its lowest value at node 7, located between nodes 6 and 8, as well as at nodes 11 and 12, which lie between nodes 10 and 13. Similarly, NDVSI demonstrates a low value at node 30, situated between nodes 29 and 31. For the lateral connecting nodes 23–24, node 24 records the minimum NDVSI value. These identified weak nodes, along with their adjacent nodes, represent suitable locations for enhancing voltage stability through the integration of distributed generators, as suggested in [36], or by deploying reactive power compensation devices.

Interestingly, the NDVSI does not necessarily follow the voltage profile in a monotonic manner; instead, it captures the system’s sensitivity characteristics rather than merely reflecting absolute voltage magnitudes. The underlying reasons and detailed analysis are provided in Section 2. Furthermore, as shown in Figure 8, the bus voltages exhibit higher magnitudes for nodes located closer to the substation.

3.2. IEEE 69-Bus Test System During Base Loading Condition

The stability indices of distribution systems are also tested on the IEEE 69-bus system to validate their effectiveness in large-scale grid applications. The line diagram of IEEE 69 bus system is illustrated in Figure 9.

Table 3. The IEEE 69-bus test system for base case loading based on stability indices.

ToL	Bus	NDVSI [36]	SI [32]	SI [33]	SI [34]
CPL	5	0.9902	0.9961	0.4982	0.9977
	13	0.7381	0.8681	0.4630	0.8734
	47	0.8473	0.9992	0.4997	0.9993
	54	0.8475	0.8904	0.4687	0.8964
	65	0.7466	0.6833	0.4128	0.6842
CIL	5	0.9904	0.9963	0.4983	0.9979
	13	0.7413	0.8753	0.4651	0.8804
	47	0.8473	0.9992	0.4997	0.9993
	54	0.8575	0.9089	0.4742	0.9137
	65	0.7591	0.7062	0.4197	0.7070
CZL	5	0.9906	0.9965	0.4984	0.9980
	13	0.7440	0.8811	0.4667	0.8860
	47	0.8473	0.9992	0.4998	0.9993
	54	0.8548	0.9039	0.4727	0.9091
	65	0.7689	0.7244	0.4251	0.7252
COML	5	0.9904	0.9963	0.4983	0.9978
	13	0.7410	0.8745	0.4648	0.8796
	47	0.8473	0.9992	0.4997	0.9993
	54	0.8511	0.8971	0.4707	0.9027
	65	0.7577	0.7035	0.4189	0.7043
EXL	5	0.9907	0.9966	0.4984	0.9980
	13	0.7437	0.8802	0.4665	0.8852
	47	0.8474	0.9992	0.4998	0.9993
	54	0.8546	0.9033	0.4725	0.9084
	65	0.7671	0.7209	0.4241	0.7217

presents the application results under the influence of various load models. The system remains stable, as no stability index approaches zero, with all indices significantly above the stability threshold (zero). It is noted that the stability indexes for the constant impedance load (CZL) and exponential load (EXL) models are higher than those corresponding to the other load models. This suggests that the system maintains a larger loading margin under these conditions. In contrast, the stability indices values associated with the constant power load (CPL) model are lower than those of the other load models, reflecting a reduced loading margin in the CPL scenario. This behavior is further confirmed in the following subsections. Additionally, the NDVSI values and bus voltages, influenced by different load models, are shown in Figure 10 and Figure 11, respectively.

Figure 10 presents the NDVSI distribution for the IEEE 69-bus system operating under normal loading conditions, providing a detailed view of the network’s voltage stability behavior. The analysis indicates that the sections covering buses 10–27 and 55–61 have the lowest NDVSI values, which reflects their relatively smaller voltage stability margins compared with other areas of the system. These regions can therefore be identified as the weakest points in the network. The NDVSI functions as a reliable and informative tool for monitoring voltage stability in distribution systems. It allows operators to assess how close each part of the system is to voltage collapse. When the NDVSI value at a particular bus approaches its critical limit (zero), corrective measures such as load reduction, reactive power compensation, or capacitor bank switching can be applied to improve system stability and prevent voltage collapse. The subsequent case studies (Section 3.3, Section 3.4, and Section 3.5) analyze the behavior of NDVSI values when the system is subjected to substantial load growth.

It is important to note that the NDVSI does not necessarily vary in a manner consistent with the voltage profile. Instead of representing absolute voltage magnitudes, this index reflects the sensitivity of the system to changes in load and network conditions. A detailed explanation of this behavior is provided in Section 2. As shown in Figure 11, buses located closer to the substation generally exhibit higher voltage magnitudes, whereas those farther away have lower voltages. Nevertheless, this variation in voltage levels does not define the characteristics of the stability index. If the stability index were to follow the voltage profile directly, it would render the use of such indices redundant, since voltage collapse in the buses cannot be determined solely from voltage magnitudes. The NDVSI thus captures system stability information beyond what is indicated by voltage levels alone, as supported by the mathematical and theoretical analysis presented in Section 2.1.

3.3. IEEE 33-Bus Test System During Different Heavy Loading Conditions and Several Load Modeling

In this scenario, a high-power load is imposed on a single bus of the IEEE 33-bus distribution system, and the stability indices are employed to evaluate the system’s voltage stability behavior under increased loading stress. Various power factors and load models are utilized to evaluate each index’s effectiveness in identifying voltage collapse points under different critical power loading conditions. The column labeled 1.0 in

Table 4. Stability indices values of the IEEE 33-bus test system during different heavy loading conditions and several-load modeling.

ToL	Critical Load @ Bus	CB	NDVSI [36]	SI [32]	SI [33]	SI [34]
CPL	P = 11.098 MW @ 22	20	0.0008	−0.0100	0.0479	0.4045
	Q = 13.672 MVAr @ 25	25	0.0270	−0.0126	0.0555	0.1112
	S = 12.42 MVA and pf = 0.765 @ 6	6	0.0004	0.0011	0.0229	0.1492
	S = 12.652 MVA and pf = 0.95 @ 6	6	0.0009	−0.0008	0.2510	0.1440
CIL	P = 18.82 MW @ 22	20	0.0018	−0.0091	0.0484	0.4054
	Q = 26.6 MVAr @ 25	25	0.0003	−0.0086	0.0374	0.0915
	S = 24.07 MVA and pf = 0.765 @ 6	6	0.0006	0.0013	0.0230	0.1501
	S = 24.5 MVA and pf = 0.95 @ 6	6	0.0023	−0.0005	0.0262	0.1449
CZL	P = 31.8 MW @ 22	20	0.0039	−0.0074	0.0493	0.4067
	Q = 45.8 MVAr @ 25	25	0.0459	0.0129	0.0581	0.1169
	S = 43.9 MVA and pf = 0.765 @ 6	6	0.0020	0.0021	0.0237	0.1514
	S = 44.8 MVA and pf = 0.95 @ 6	6	0.0026	−0.0005	0.0266	0.1454
COML	P = 16.25 MW @ 22	20	0.0083	−0.0034	0.0510	0.4087
	Q = 21.6 MVAr @ 25	25	0.0078	−0.0051	0.0405	0.0950
	S = 20 MVA and pf = 0.765 @ 6	6	0.0070	0.0048	0.0258	0.1533
	S = 20.5 MVA and pf = 0.95 @ 6	6	0.0007	−0.0013	0.0254	0.1441
EXL	P = 22.8 MW @ 22	20	0.0108	−0.0014	0.0522	0.4103
	Q = 49.99 MVAr @ 25	25	0.1272	0.1274	0.1394	0.2319
	S = 39 MVA and pf = 0.765 @ 6	6	0.0078	0.0016	0.0294	0.1472
	S = 34 MVA and pf = 0.95 @ 6	6	0.0000	−0.0060	0.0300	0.1407

indicates the type of load (ToL). For clarification, in the CPL case, all loads in the system are modeled as constant power loads under the base loading condition, and the heavy loading scenario is applied to a single node to evaluate system stability in this configuration. The same procedure is followed for the CZL, CIL, and EXL models, where each type of load is considered independently to ensure a consistent basis for comparison.

For the composite load (COML), also referred to as the ZIP model, the load composition at the base case is defined as 40% CPL, 30% CIL, and 30% CZL, representing the typical mixture of load components. The increased loading is then applied to a single node of the IEEE 33-bus system to investigate the performance of the stability indices in assessing voltage stability under this mixed load condition.

As shown in Table 4, the NDVSI [36] demonstrates high accuracy and robustness in identifying voltage collapse points across different load types (ToL) and under a range of loading conditions with varying power factors, confirming its strong diagnostic effectiveness. The NDVSI [36] demonstrates superior performance in assessing voltage stability, as it consistently reaches the stability limit (zero) in all the tested cases, including CPL, CIL, CZL, COML, and EXL. This behavior indicates the NDVSI’s robustness in accurately capturing the critical stability conditions of the system across various loading scenarios. In comparison, the results are validated by SI [33], which also approaches zero, indicating the recognition of critical load conditions. However, the NDVSI [36] consistently provides a closer and more reliable approximation to the stability limit, offering a more nuanced and accurate evaluation of voltage stability.

On the other hand, SI [32] also approaches the stability limit but exhibits a significant drawback: in most cases, it surpasses the stability threshold and yields negative values. These negative values are problematic because they signify that voltage collapse has already occurred, which renders the index ineffective in predicting the onset of instability before the collapse. This limitation is particularly critical in practical applications, where early detection of instability is crucial for implementing preventive measures. In contrast, the NDVSI [36] shows a more timely and accurate indication of the system’s proximity to instability, offering a crucial advantage in voltage stability assessment and ensuring better preparedness for maintaining system stability.

The results indicate that SI [34] demonstrates the poorest performance among the stability indices evaluated. In most cases, its values fail to approach the stability limit under critical loading conditions, which compromises its effectiveness in accurately assessing voltage stability. This limitation suggests that SI [34] is less responsive to changes in load conditions and may not provide reliable indications of impending instability, especially under high-load scenarios. The results show that the critical active, reactive, and apparent power loadings for each type of load are different. The CZL shows the maximum critical loading (maximum loading margin). On the other hand, the CPL presents the minimum maximum allowable load. The critical loadings for each type of load are tabulated in Table 4.

Figure 12 illustrates the variation in the most effective index (NDVSI) as active and reactive power gradually increase at bus 6 with a constant power load. The NDVSI [36] value at the base loading case is 0.86096, and it decreases gradually as both active and reactive power increase, maintaining a constant power factor of 0.765 until the critical load is reached. At the critical load (12.42 MVA with pf = 0.765), the critical stability point (NDVSI) is 0.0004. Additionally, the voltage profile at node 6 is determined during the variation in active and reactive power, as shown in Figure 13. The voltage at the base loading case at bus 6 is 0.9495 pu. It gradually decreases as both active and reactive power loads increase, maintaining a constant power factor of 0.765. The voltage reaches the critical point (V = 0.57072 pu) when the load approaches the critical level (12.42 MVA), as shown in Figure 13.

3.4. Voltage Stability Assessment of the IEEE 69-Bus System Under Heavy Loading Conditions and Various Load Models

The voltage stability indices are further evaluated using the IEEE 69-bus radial distribution system to verify their performance under diverse operating conditions and load configurations. The same load modeling methodology employed for the IEEE 33-bus system is applied here, where each load type, including CPL, CIL, CZL, COML (ZIP), and EXL, is analyzed independently to ensure consistency and accuracy in parameter assessment. In all cases, the system loads are modeled according to the respective load type under base loading conditions, and a heavy loading scenario is introduced at a single node to assess the ability of the indices to identify critical loading levels and potential voltage collapse points. Furthermore, the system is tested under high active, reactive, and apparent power demands with varying power factors to comprehensively evaluate the robustness, precision, and practicality of each index across multiple operating scenarios.

A variety of scenarios are tested across different models to comprehensively evaluate the effectiveness of the indices in voltage stability assessment. These scenarios include multiple load models and varying operating conditions. The indices are designed to signal safe system operation when their values are significantly above zero, while values approaching zero indicate that the system is nearing instability and requires corrective action.

Results in

Table 5. Stability indices values of the IEEE 69-bus test system during different heavy loading conditions and several-load modeling.

ToL	Critical Load @ Bus	CB	NDVSI [36]	SI [32]	SI [33]	SI [34]
CPL	P = 13.406 MW @ 12	12	0.0651	0.0280	0.0462	0.0874
	Q = 12.08 MVAr @ 57	57	0.0009	0.0168	0.0959	0.1928
	S = 18.805 MVA and pf = 0.7 @ 43	41	0.0004	−0.0008	0.0333	0.3427
	S = 19.24 MVA and pf = 0.85 @ 43	41	0.0009	0.0009	0.0385	0.3498
CIL	P = 28.51 MW @ 12	12	0.0472	0.0188	0.0363	0.0783
	Q = 20.25 MVAr @ 57	57	0.0001	0.0148	0.1025	0.1951
	S = 31.6 MVA and pf = 0.7 @ 43	41	0.0004	−0.0008	0.0333	0.3427
	S = 31.8 MVA and pf = 0.85 @ 43	41	0.0005	0.0006	0.0384	0.3496
CZL	P = 55.5 MW@ 12	12	0.0641	0.0275	0.0456	0.0896
	Q = 32.1 MVAr @ 57	57	0.0014	0.0149	0.1070	0.1977
	S = 53 MVA and pf = 0.7 @ 43	41	0.0010	−0.0002	0.0336	0.3431
	S = 52.5 MVA and pf = 0.85 @ 43	41	0.0006	0.0007	0.0384	0.3497
COML	P = 22.10 MW @ 12	12	0.0588	0.0247	0.0427	0.0850
	Q = 17.80 MVAr @ 57	57	0.0093	0.0227	0.1057	0.2013
	S = 27.47 MVA and pf = 0.7 @ 43	41	0.0006	−0.0007	0.0334	0.3428
	S = 27.80 MVA and pf = 0.85 @ 43	41	0.0027	0.0025	0.0393	0.3509
EXL	P = 41.2 MW @ 12	12	0.0154	0.0042	0.0193	0.0615
	Q = 38.25 MVAr @ 57	57	0.0957	0.0990	0.0861	0.2552
	S = 51.1 MVA and pf = 0.7 @ 43	41	0.0011	−0.0003	0.0438	0.3553
	S = 44.7 MVA and pf = 0.85 @ 43	41	0.0010	−0.0032	0.0498	0.3605

clearly demonstrate the superior performance of NDVSI [36] compared to other stability indices in precisely detecting the system’s critical operating conditions. These findings highlight the index’s ability to reliably detect points of instability, offering valuable insights for monitoring the stability of the power grid under varying conditions. Power flow analyses are performed by progressively increasing the load at selected buses until the power flow fails to converge, which signifies the point of crucial loading. At this point, all stability indices are expected to approach the stability limit (zero).

Among all tested indexes, the NDVSI [36] consistently demonstrates superior accuracy and reliability. For every load model under critical conditions, NDVSI [36] values closely approach zero, offering a clear and precise indication of impending voltage instability. In contrast, SI [32] frequently exceeds the stability threshold and drops into negative values, falsely indicating that collapse has already occurred before reaching the actual critical point, highlighting a major drawback in its predictive capability.

While SI [33] does produce values near zero, lending some support to the NDVSI results, its performance is slightly less accurate, as it does not consistently align as closely with the stability boundary. Notably, SI [34] performs the weakest among the compared indices, failing to obtain the stability limit in most of the critical loading scenarios, thereby limiting its usefulness in monitoring voltage stability assessment.

Additionally, the application results highlight the system’s varying sensitivity to different load types. The highest critical loading margin is observed under CZL, while CPL yields the lowest, demonstrating the importance of accounting for load type in stability assessments. Table 5 effectively illustrates the capability of NDVSI [36] to detect critical loading conditions with high precision across various power factors and load models, affirming its superiority as a robust voltage stability indicator.

3.5. Loading Margin

The power flow study is conducted by incrementally scaling up the load across all buses through a load multiplier denoted as k, with λ indicating the initial loading condition for the base case. As the load increases, the power flow solution becomes unsolvable once the system reaches its critical loading point. At this point, voltage stability indexes are expected to approach their stability threshold, zero, indicating proximity to voltage instability.

Table 6. Critical loading and load margin (LM) of IEEE 33 and 69 bus test systems at different load models.

Model	ToL	Load Factor ${\mathit{\lambda }}_{\mathbf{max}}=\mathit{k}\mathit{\lambda }$	LM (MVA)	CB	NDVSI [36]	SI [32]	SI [33]	SI [34]
IEEE 33-bus	CPL	${\lambda }_{\max }=3.412\lambda$	10.54	17	0.0243	0.0333	0.0847	0.0361
	CIL	${\lambda }_{\max }=6.98\lambda$	26.13	17	0.0857	0.0224	0.0700	0.0241
	CZL	${\lambda }_{\max }=15.38\lambda$	62.84	17	0.0833	0.0192	0.0638	0.0194
	COML	${\lambda }_{\max }=5.4\lambda$	19.23	17	0.0849	0.0230	0.0703	0.0249
	EXL	${\lambda }_{\max }=11.45\lambda$	45.56	17	0.0780	0.0190	0.0653	0.0203
IEEE 69-bus	CPL	${\lambda }_{\max }=3.212\lambda$	10.31	57	0.0881	0.0704	0.0574	0.2027
	CIL	${\lambda }_{\max }=6.49\lambda$	25.58	57	0.0769	0.0680	0.0782	0.1901
	CZL	${\lambda }_{\max }=13.2\lambda$	56.85	57	0.0748	0.0767	0.0754	0.1801
	COML	${\lambda }_{\max }=5.11\lambda$	19.15	57	0.0843	0.0741	0.0722	0.1981
	EXL	${\lambda }_{\max }=9.62\lambda$	40.28	57	0.0896	0.0691	0.0604	0.1990

demonstrates that the majority of the evaluated indices successfully detect the critical condition as their values approach the threshold of voltage stability under heavily loaded scenarios. However, SI [34] consistently underperforms, failing to obtain the stability threshold in several critical load cases.

Moreover, the analysis shows that the system exhibits the highest loading margin when operating under CZL, highlighting its greater resilience to increased demand. Under the CZL configuration, the critical loading levels reach 15.38 and 13.2 times the base case for the 33-bus and 69-bus IEEE test networks. Correspondingly, the associated loading margins are 62.84 MVA for the 33-bus system and 56.85 MVA for the 69-bus system. In contrast, the lowest loading margins are observed under the CPL scenario, registering values of 10.54 and 10.31 for the 33-bus and 69-bus IEEE networks, respectively.

Furthermore, the critical buses (CB) are identified under various load models at the critical loading conditions, as illustrated in Table 6. The loading margin, when ranked across different load models, follows the order: CZL > EXL > CIL > COML > CPL. These findings demonstrate the efficacy and reliability of the stability indices except SI [34] in accurately identifying loading margins across multiple radial power systems and under various load modeling scenarios.

4. Conclusions

This paper introduces a comparison study between four voltage stability indices, designed to assess voltage stability in radial power distribution networks. Monitoring and evaluating voltage stability in these systems are essential for ensuring the uninterrupted dispatching of power loads and guaranteeing the reliable, seamless operation of the system. The proposed comparative study prioritizes system security and stability monitoring, offering insights into the system’s condition before voltage collapse occurs. The application results show that, the NDVSI [36] serves as a proactive tool for alerting operators to potential voltage collapses and cascading outages, providing a critical early warning mechanism. The effectiveness of the NDVSI [36] is demonstrated through its ability to identify critical buses in two different electrical systems under a range of operating load conditions and varying power factors. As long as the system remains stable, this approach proves to be highly adaptable and capable of accommodating changes in both topology and load within the network. This adaptability makes the NDVSI [36] a valuable tool for enhancing the reliability, security, and stability of power distribution grids.

The comprehensive results obtained from the two IEEE systems, which include various load models, critical loading conditions, and power factor variations, clearly confirm the accuracy and effectiveness of NDVSI [36] when compared to other voltage stability indices. This outcome stems from the formulation of the NDVSI [36], which incorporates all essential parameters of distribution network lines, excluding the shunt admittance component, as it is generally insignificant in radial distribution configurations. Moreover, the NDVSI [36] accounts for the voltage angle difference, a factor often neglected by the other existing stability indices. This highlights the limitation of the other indices, which are based on approximate models, while the NDVSI [36] relies on a precise representation of radial distribution systems.

Moreover, an in-depth comparative analysis has been carried out between the four indices (NDVSI [36], SI [32], SI [33], and SI [34]) considering multiple dimensions, including theoretical foundations, underlying assumptions, mathematical formulations, distinctive characteristics, threshold behaviors, and the influence of excluding certain parameters. Through different load modeling and operating conditions, the findings show the superiority of the NDVSI [36] and its capability to accurately identify key system parameters, including the maximum allowable load at each node (critical load), loading margin (MVA), voltage collapse points and critical buses (CB).

Near the voltage collapse points, the application results demonstrate that the NDVSI [36] approaches zero, in contrast to the stability indices SI [32], SI [33], and SI [34], which either cross zero (resulting in negative values) or remain above zero. This indicates that the indices fail to capture the voltage instability phenomenon accurately in certain scenarios. On the other hand, the NDVSI [36] delivers more precise and reliable results for assessing voltage stability. The NDVSI emerges as a promising tool for evaluating voltage stability across various load models and operating conditions, offering enhanced accuracy and predictive capability in voltage stability assessments.

5. Future Works

Integration with Distributed Generation (DG): Recent studies show that NDVSI can effectively identify weak buses and their neighboring nodes, supporting optimal DG placement and sizing [36]. Future research can focus on improving voltage stability through NDVSI by integrating multiple DG sources while considering load variability, renewable generation, and system reconfiguration. Adaptive algorithms that adjust DG placement and sizing based on real-time NDVSI evaluation could further enhance system performance and reliability.

Consideration of Uncertainty and Stochastic Elements: Incorporating uncertainty and stochastic factors such as variable renewable generation and unpredictable load patterns into NDVSI-based assessment could strengthen voltage stability evaluation and improve the resilience of modern power systems.