Modeling the Dynamics of Supercapacitors by Means of Riemann–Liouville Integral Definition

Abstract

The application of fractional calculus to obtain dynamic models for supercapacitors represents an alternative approach to obtaining simpler and more accurate models. This paper presents a model for the supercapacitor in the time domain, based on the use of the fractional or non-integer order integral. This fractional model is compared with the conventional simple model, which is typically used in industrial applications. This fractional integral-based model provides satisfactory fits in relation to the number of parameters used in the model. Furthermore, an interpretation of the effect of the application of fractional integration is presented for constant current charging and discharging processes at constant current, using the Riemann–Liouville definition for the non-integer order integral. Supercapacitors are devices that exhibit non-linear behavior, with a distinct charging and discharging operation. There are several methods of dynamic analysis for the characterization of supercapacitors. The information extracted from these methods is essential for understanding the behavior of supercapacitors and, thus, ensuring that processes involving supercapacitors are as efficient as possible. This paper presents a dynamic analysis based on charge and discharge operations with constant currents. The conclusion is that the fractional model provides fairly accurate fits.

1. Introduction

The supercapacitor is a device that has emerged with the potential to improve energy storage systems [1,2]. They behave in a similar way to conventional capacitors, but have a larger electrode contact surface, which means higher capacitances. This leads to higher energy densities than conventional capacitors, and they are also characterized by higher power densities than batteries.

Supercapacitors typically have energy densities in the order of 300 times higher than conventional capacitors, and two-tenths that of batteries with lower energy densities. However, their power densities are 10 times higher than most batteries. Thanks to their energy and power densities, together with the associated low series resistance, they are an intermediate between batteries and conventional capacitors.

Supercapacitors are also known as ultracapacitors. Energy is stored by polarizing an electrolyte solution, although it is an electrochemical device in which virtually no chemical reactions occur in its energy storage mechanism. This mechanism is highly reversible, allowing the supercapacitors to be charged and discharged hundreds of thousands of times.

Supercapacitors are employed in automotive applications, serving as supplementary energy storage systems [3,4], hybrid energy systems [5,6,7,8], DVD players, computers, and other electronic equipment.

Supercapacitors are elements that exhibit non-linear behavior and undergo distinct charging and discharging processes. Obtaining accurate models for supercapacitors is crucial, as this enables the attainment of high efficiencies in their utilization in diverse industrial applications. This paper presents an analysis of the dynamics of supercapacitors for charging and discharging operations with constant currents.

The objective is to obtain simple models of the dynamics of electrochemical capacitors by using the non-integer or fractional order integral, which offer better fits than conventional models.

This paper is structured as follows: Section 2 provides a brief introduction to the applications of fractional calculus; Section 3 presents a brief description of supercapacitors; Section 4 presents the models analyzed in this article for the supercapacitors, and presents the identification method in the time domain to obtain the model parameters; Section 5 shows the materials and methods; Section 6 shows the results of the tests carried out; and, finally, Section 7 shows the conclusions.

2. Introduction to the Application of Fractional Calculus

The concept of the non-integer derivative is as old as conventional differential calculus. Fractional calculus has been employed to model a range of physical phenomena [9]. Additionally, it has been utilized in the field of control theory [10,11].

In nature, numerous systems exhibit fractional behavior, although many of these systems exhibit only slight fractionality. In this context, multi-problem solving techniques are proposed in [12]. Furthermore, the modeling of anomalous diffusion phenomena, defined in accordance with the fractional Fokker–Planck equation [13].

There are numerous real-world applications of fractional calculus, including the control of power converters [14], the modeling of mechanical systems [15,16], the description of viscoelastic materials using fractional models [17], the study of dielectrics [18], and electrochemical identification techniques (fruits, vegetables, fuel cells, batteries, supercapacitors) [19,20,21,22,23,24].

3. Supercapacitor Features

A supercapacitor has two porous, non-reactive electrodes immersed in an electrolyte, with a separator between the electrodes that allows ions to move across it.

Energy is stored in the form of separate charges in the electrochemical double layer formed at the interface. The thickness of the double layer depends on the concentration of the electrolyte and the size of the ions, and the capacitance values are contingent upon the ratio of ion sizes between the molecules [25]. On the other hand, the electrodes are made of porous materials with a high surface area, the size of these pores being of the order of nanometers, giving specific surface areas between 500 and 2000 ${\displaystyle \frac{{\mathrm{m}}^2}{\mathrm{g}}}$, and specific capacities for carbon electrodes of 75–175 F/g for aqueous electrolytes and 40–100 F/g for organic electrolytes [1,2].

Ions are transferred between the electrodes during charging and discharging by diffusion through the electrolyte.

4. Dynamic Characteristics of Supercapacitors

Figure 1 illustrates the voltage evolution of an electrochemical capacitor (Panasonic 50 F) when a constant current is applied (at the top charge current, $i_{charge}=3$ A, and at the bottom discharge current, $i_{discharge}=-3$ A). It can be observed that the response to the constant current is not linear, as would be expected for a capacitor. This non-linear behavior can be observed in the non-proportional variation of the voltage with respect to the integral of the current. It is also important to note that the behavior of the electrochemical capacitor for charging differs from that for discharging.

A variety of dynamic models for electrochemical capacitors have been employed in a number of industrial applications. These include simple $RC$ models based on circuits with an equivalent series resistor and an ideal capacitor [26,27,28,29,30,31], as well as models composed of $RC$ networks of resistors and capacitors [32,33], and finally models based on variable capacitances (voltage-dependent $C\left(v\right(t\left)\right)$), which involve differential equations with variable coefficients [34,35].

This paper proposes an alternative model based on the non-integer or fractional order integral, which achieves a satisfactory fit of the data in relation to the number of parameters used in the model. Furthermore, the impact of fractional integration on the electrochemical capacitor’s behavior when charged or discharged at a constant current is elucidated, employing the definition of the Riemann–Liouville integral.

4.1. Fractional Modeling

From Figure 1 and the typical response of the simple $RC$ capacitor model, it can be established that the behavior of the electrochemical capacitor at constant current is non-linear and differs from that of the conventional model.

Figure 2 and Figure 3 illustrate the simulation of the conventional $RC$ model in comparison to the fractional model, for constant charge and discharge profiles. The analysis of these figures indicates that the following expression accurately represents the response of the supercapacitor:

$$\mathsf{\Delta }v\left(t\right)=Ri\left(t\right)+\mathsf{\Delta }{v}_c\left(t\right)$$

(1)

The behavior of $\mathsf{\Delta }{v}_c\left(t\right)$ differs between charging and discharging operations, and there is no linear relationship between the integral of the current $i\left(t\right)$ and the aforementioned variable. Consequently, the following expressions may be considered for the charging and discharging operations:

$$v\left(t\right)=v\left(0\right)+R_{\alpha }i\left(t\right)+\mathsf{\Delta }{v_c}_{\alpha }\left(t\right),i\left(t\right)>0$$

(2)

$$v\left(t\right)=v\left(0\right)+R_{\beta }i\left(t\right)+\mathsf{\Delta }{v_c}_{\beta }\left(t\right),i\left(t\right)<0$$

(3)

In expressions (2) and (3), the parameters $R_{\alpha }$ and $R_{\beta }$ are equivalent series resistances. Conversely, the terms $\mathsf{\Delta }{v_c}_{\alpha }\left(t\right)$ and $\mathsf{\Delta }{v_c}_{\beta }\left(t\right)$ are linked to the fluctuations in the stored electric charge, which consequently influence the current $i\left(t\right)$. These terms exhibit a linear relationship in the conventional model ($RC$), as a uniform storage of the electric charge in the capacitor results in a uniform variation in the voltage in the capacitor. However, in the case of the supercapacitor, the storage of the electric charge and the voltage variation are not uniform. That is to say, identical amounts of electric charge do not cause the same voltage variation.

This paper proposes the use of the non-integer order integral of the current ($i\left(t\right)$) to associate it with the non-uniform behavior of the voltage variation with respect to a constant current. Consequently, the following linear relationship is demonstrated below, as a consequence of the utilization of the non-integer order integral.

$$\mathsf{\Delta }{v_c}_{\alpha }\left(t\right)={\displaystyle \frac{\mathsf{\Delta }{q}_{\alpha }\left(t\right)}{C_{\alpha }}}={\displaystyle \frac{{}_{0}I_t^{\alpha }i\left(t\right)}{C_{\alpha }}}$$

(4)

$$\mathsf{\Delta }{v_c}_{\beta }\left(t\right)={\displaystyle \frac{\mathsf{\Delta }{q}_{\beta }\left(t\right)}{C_{\beta }}}={\displaystyle \frac{{}_{0}I_t^{\beta }i\left(t\right)}{C_{\beta }}}$$

(5)

where $C_{\alpha }$ and $C_{\beta }$ are constant.

Using non-integer order integral, expressions (2) and (3) are in the following forms:

$$v\left(t\right)=v\left(0\right)+R_{\alpha }i\left(t\right)+{\displaystyle \frac{1}{C_{\alpha }}}{i}^{(-\alpha )}\left(t\right),i\left(t\right)>0$$

(6)

$$v\left(t\right)=v\left(0\right)+R_{\beta }i\left(t\right)+{\displaystyle \frac{1}{C_{\beta }}}{i}^{(-\beta )}\left(t\right),i\left(t\right)<0$$

(7)

The non-integer order integral has been employed to derive a non-integer order equation with constant coefficients ($R_{\alpha }$, ${\displaystyle \frac{1}{C_{\alpha }}}$, $R_{\beta }$, ${\displaystyle \frac{1}{C_{\beta }}}$), which accounts for the charging and discharging behavior of the supercapacitor.

Given that the fractional integral of a constant is [9],

$${}_{0}I_t^{\alpha }C={\displaystyle \frac{C}{\Gamma (1+\alpha )}}{t}^{\alpha }$$

(8)

it is possible to solve the expressions (6) and (7) as follows:

• For a constant current greater than zero ($i\left(t\right)=i>0$):

  $$v\left(t\right)=v\left(0\right)+R_{\alpha }i\left(t\right)+{\displaystyle \frac{1}{C_{\alpha }}}{\displaystyle \frac{i}{\Gamma (1+\alpha )}}{t}^{\alpha },i\left(t\right)>0$$

  (9)
• For a constant current less than zero ($i\left(t\right)=i<0$):

  $$v\left(t\right)=v\left(0\right)+R_{\beta }i\left(t\right)+{\displaystyle \frac{1}{C_{\beta }}}{\displaystyle \frac{i}{\Gamma (1+\beta )}}{t}^{\beta },i\left(t\right)<0$$

  (10)

The Riemann–Liouville definition of the non-integer order integral provides insight into the derivation of the linear relationship through the use of the non-integer order integral. The non-integer order integral of the current, as defined by the Riemann–Liouville definition, is presented below.

$${}_{0}I_t^{\alpha }i\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\alpha \right)}}{\int }_0^{t}i\left(\tau \right){(t-\tau )}^{(\alpha -1)}d\tau ,t>0,\alpha \in {\mathbb{R}}^{+}$$

(11)

The Riemann–Liouville integral is a convolution, which by itself does not give much information about the behavior of the supercapacitor, but if a transformation is applied on the time scale such as the following [36]:

$$g_t\left(\tau \right)={\displaystyle \frac{1}{\Gamma (\alpha +1)}}\left[t^{\alpha }-{(t-\tau )}^{\alpha }\right]$$

(12)

it is possible to arrive at the following integral:

$${}_{0}I_t^{\alpha }i\left(t\right)={\int }_0^{t}i\left(\tau \right)d{g}_t\left(\tau \right)$$

(13)

The difference between the integrals (11) and (13) can be seen in Figure 4, obtained from simulations, with the upper part showing the voltage $v\left(\tau \right)$ versus $g_t\left(\tau \right)$, on the conventional time scale, and the lower part showing the voltage $v\left(\tau \right)$ versus $g_t\left(\tau \right)$, on a transformed time scale. The latter curve shows a linear relationship between the integral of the current $i\left(t\right)$, and the variation of the voltage $\mathsf{\Delta }{v_c}_{alpha}\left(t\right)$.

In summary, it can be stated that the non-integer order integral enables the construction of a model that can provide fits to real data with reduced error, with a small number of parameters, for the purposes of charging and discharging at a constant current.

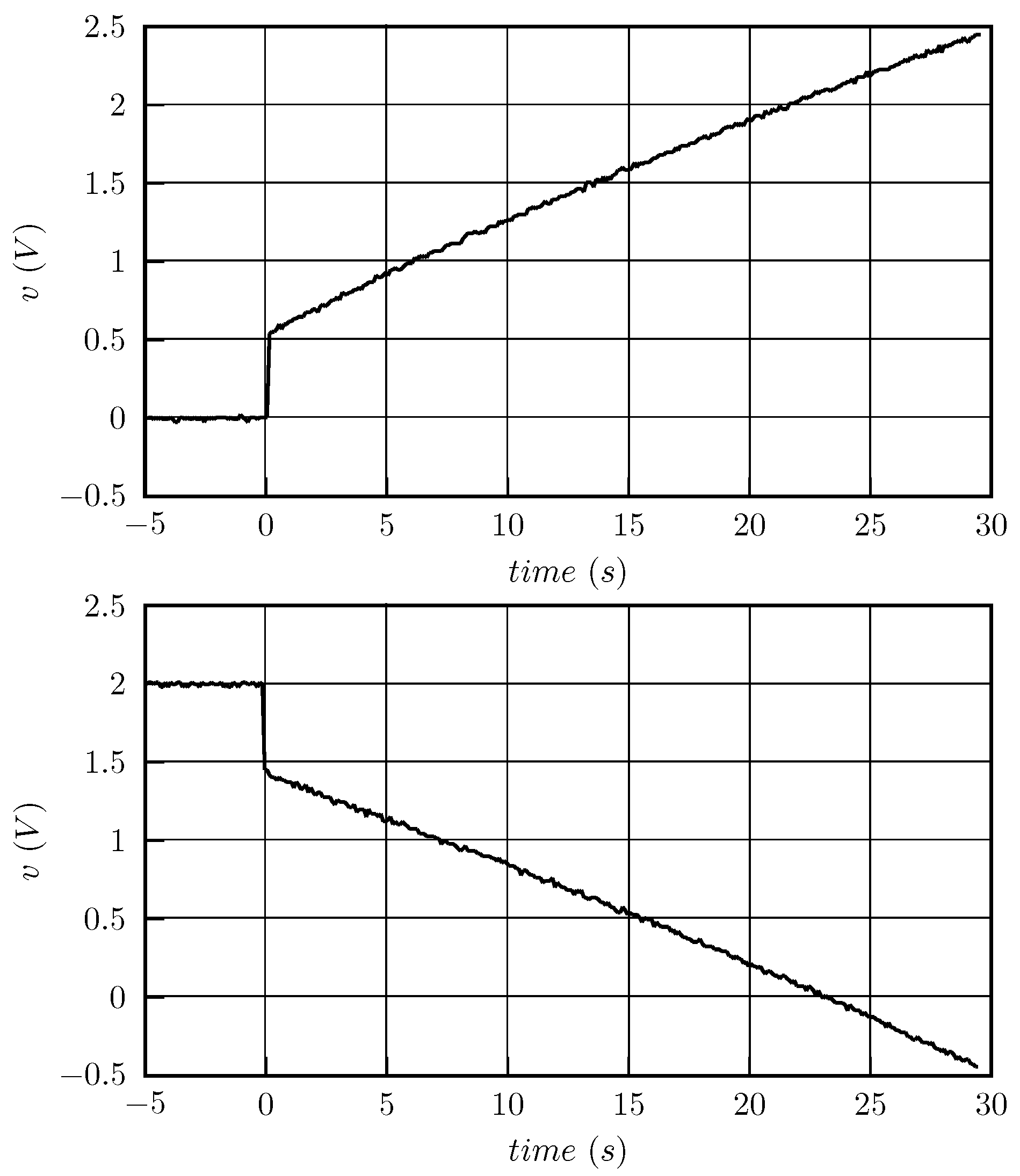
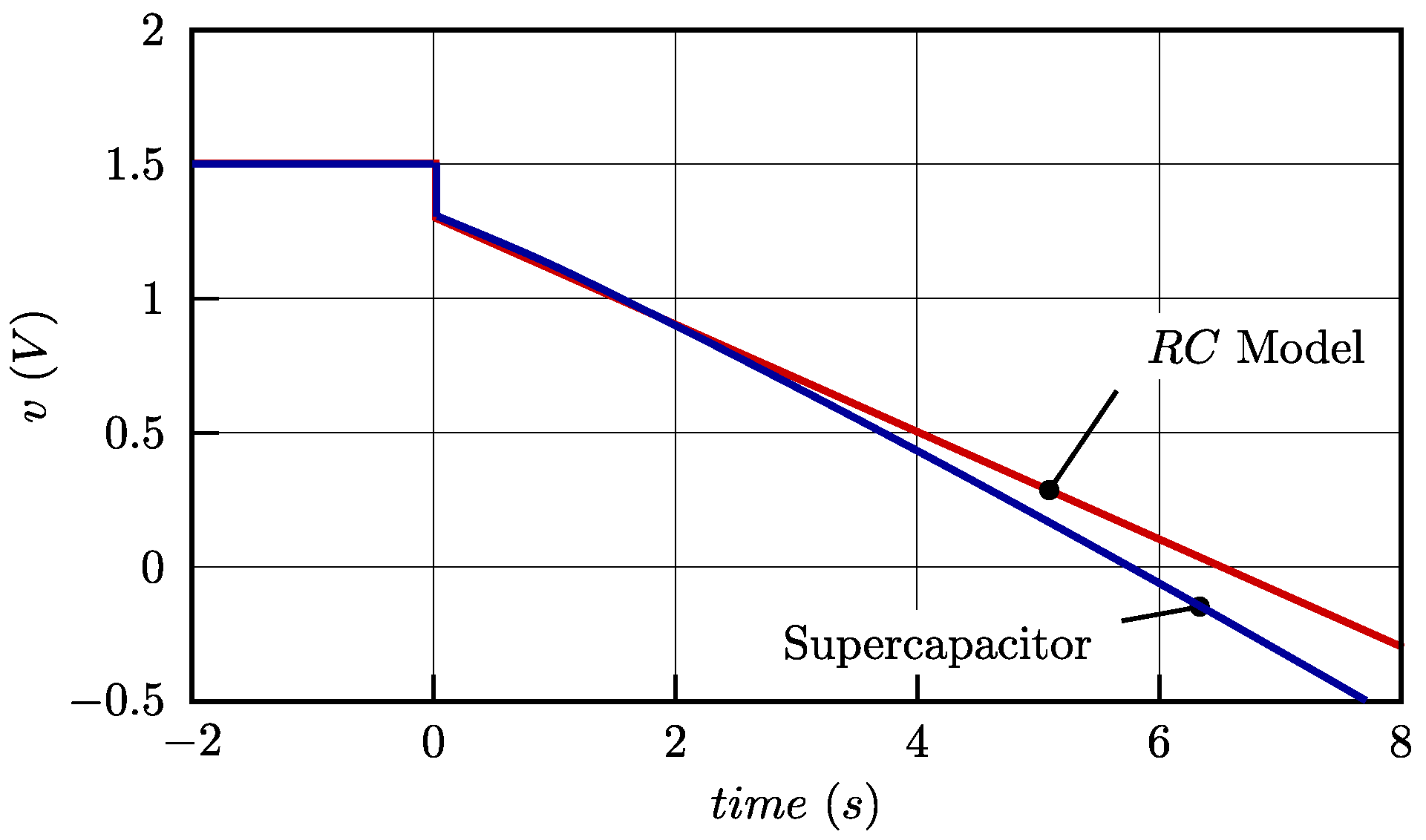
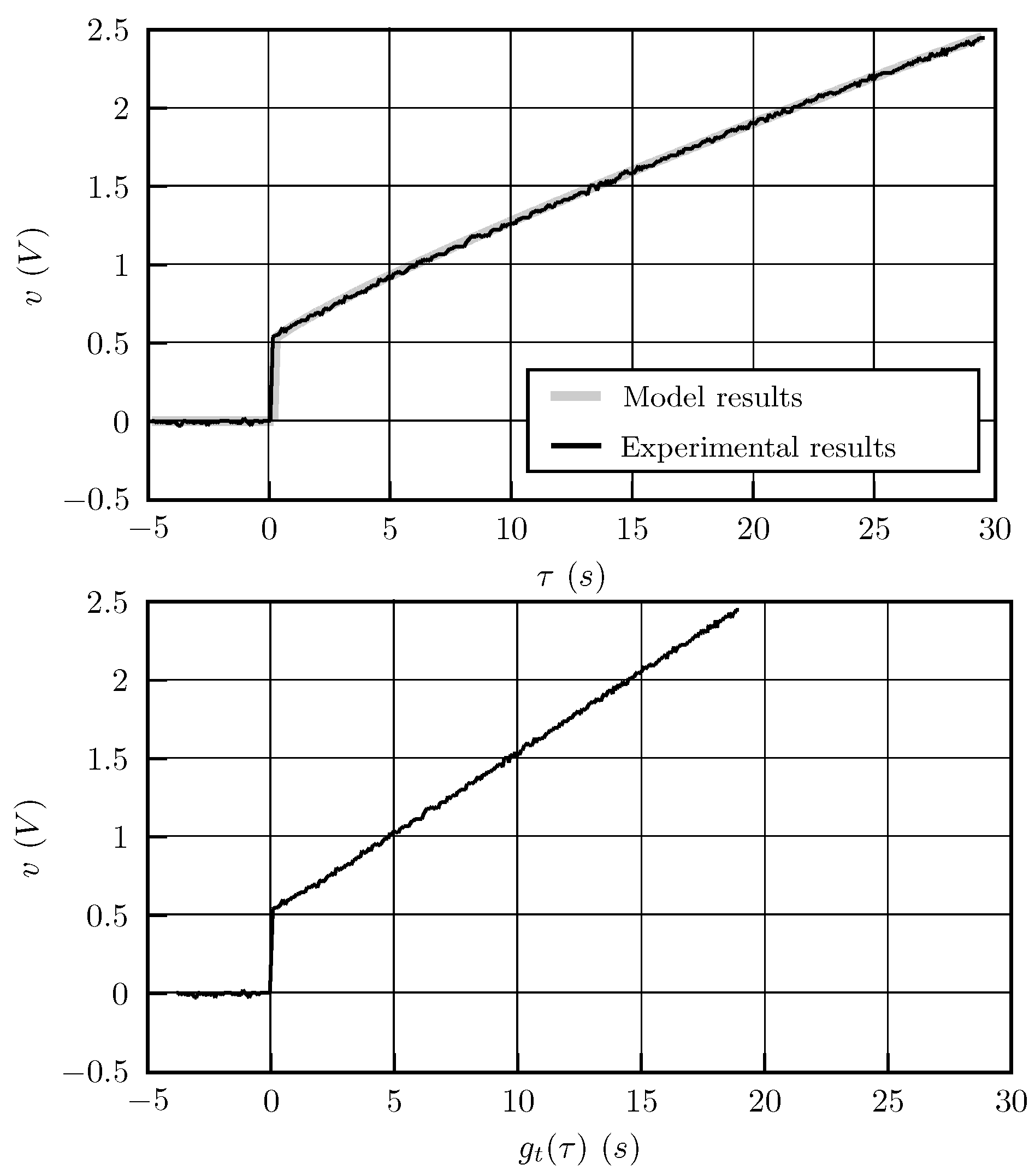
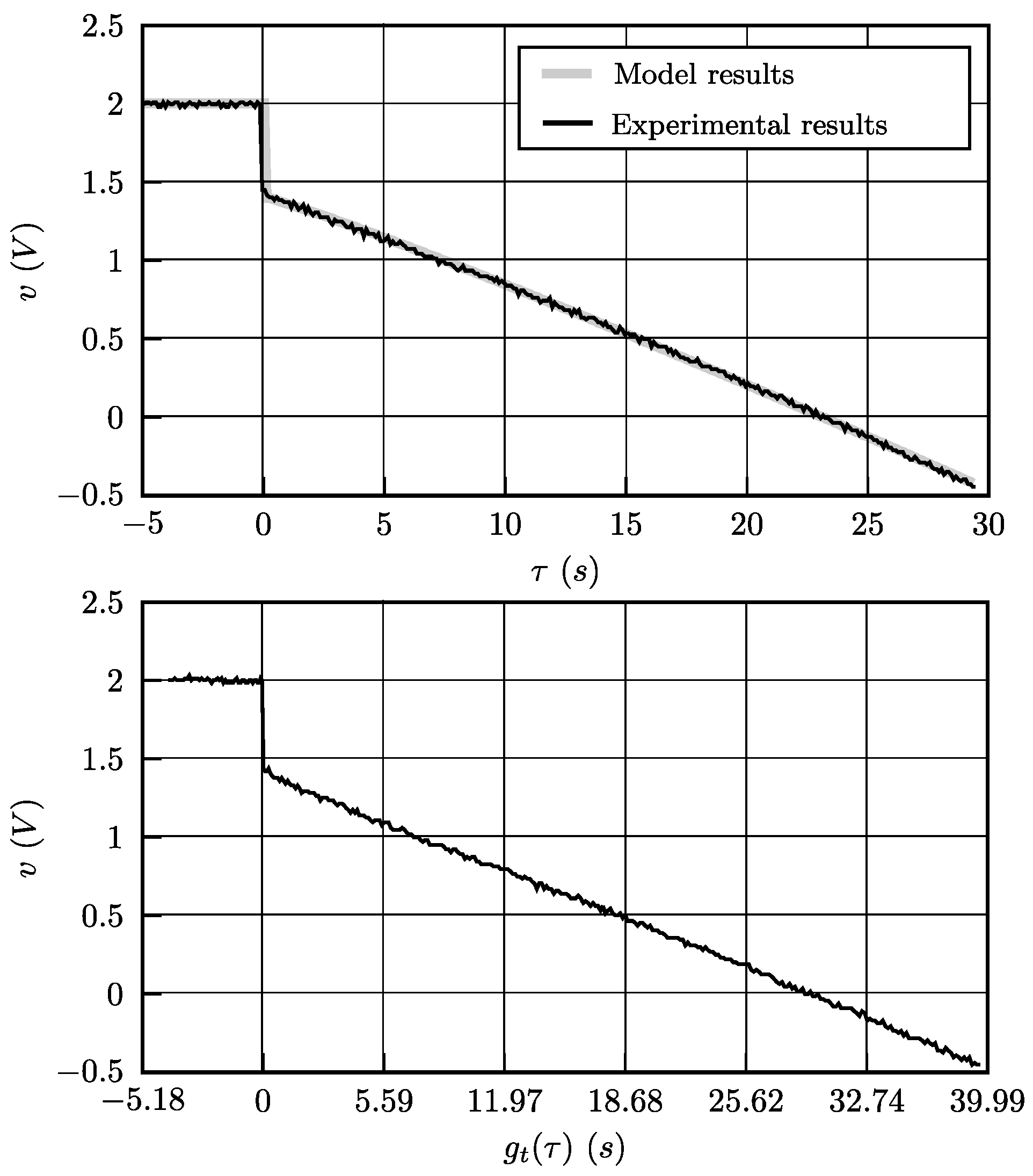
4.2. Model Validation Method

For the determination of the parameters of the supercapacitor ($R_{\alpha }$, $C_{\alpha }$, $R_{\beta }$, $C_{\beta }$), the procedure developed in article [37] is used. To carry out the identification, the Grünwald–Letnikov approximation has been made use of for the non-integer order derivative [9] to obtain a numerical solution of the fractional integral (6) and (7), using the following expression:

$${}_{0}I_t^{\alpha }f\left(t\right)\approx h^{\alpha }\sum _{j=0}^k{b}_{j}f(kh-jh)$$

(14)

$$b_j={(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{-\alpha }{j}}\right)$$

(15)

where $\left({\displaystyle \genfrac{}{}{0pt}{}{-\alpha }{j}}\right)$ is a binomial coefficient. To determine the coefficients $b_j$, use of the following approach is proposed [9]:

$$b_j=\left(1-{\displaystyle \frac{1-\alpha }{j}}\right)b_{j-1},\mathrm{for}j=1,2,3,\dots N;b_0=1$$

(16)

The numerical approximation of Equation (6) is shown below, with a discreet time $t_m(m=2,3,\dots )$,

$$\mathsf{\Delta }{v}_m=R_{\alpha }{i}_m+{\displaystyle \frac{1}{C_{\alpha }}}{i}_m^{(-\alpha )}$$

(17)

Only the charging operation is shown, because the numerical approximation is identical for the case of the discharging operation. Applying the Grünwald–Letnikov approximation, we obtain

$$\mathsf{\Delta }{v}_m=R_{\alpha }{i}_m+{\displaystyle \frac{1}{C_{\alpha }}}{h}^{\alpha }\sum _{j=0}^m{b}_j{i}_{m-j}$$

(18)

In order to achieve identification with the fractional model, the following functional has been used:

$$E\left(\overline{a}\right)=\underset{0}{\overset{T}{\int }}{[a_1{i}^{(-\alpha )}\left(t\right)+a_{0}i\left(t\right)-\mathsf{\Delta }v\left(t\right)]}^{2}dt\approx min$$

(19)

With this functional, the coefficients of the equation can be determined from the experimental data ($i\left(t\right),v\left(t\right)$). The necessary condition to obtain the minimum of this functional is

$${\displaystyle \frac{\partial E\left(\overline{a}\right)}{\partial \overline{a}}}=0$$

(20)

If the continuous functions $\mathsf{\Delta }v\left(t\right)$ and $i\left(t\right)$ are replaced by their discrete equivalents, furthermore, the integrals are replaced by summations for the time interval of operation, which remains unchanged, like in (21).

$$\begin{array}{c}{a}_1{\displaystyle \sum _{m=0}^M}{\left(i_m^{(-\alpha )}\right)}^2+a_0{\displaystyle \sum _{m=0}^M}{i}_m{i}_m^{(-\alpha )}={\displaystyle \sum _{m=0}^M}\mathsf{\Delta }{v}_m{i}_m^{(-\alpha )}\hfill \\ \\ a_1{\displaystyle \sum _{m=0}^M}{i}_m^{(-\alpha )}{i}_m+a_0{\displaystyle \sum _{m=0}^M}{i}_m^2={\displaystyle \sum _{m=0}^M}\mathsf{\Delta }{v}_m{i}_m\hfill \end{array}$$

(21)

The parameters $\overline{a}$ can be determined from the system of Equation (21) by means of an iterative process of calculation. In order to obtain these parameters, and also the non-integer order of the integral $\alpha$, it is necessary to carry out this process. This is due to the fact that the system of equations given in Equation (21) is non-linear. The iterative method is developed in greater detail in the aforementioned paper [37].

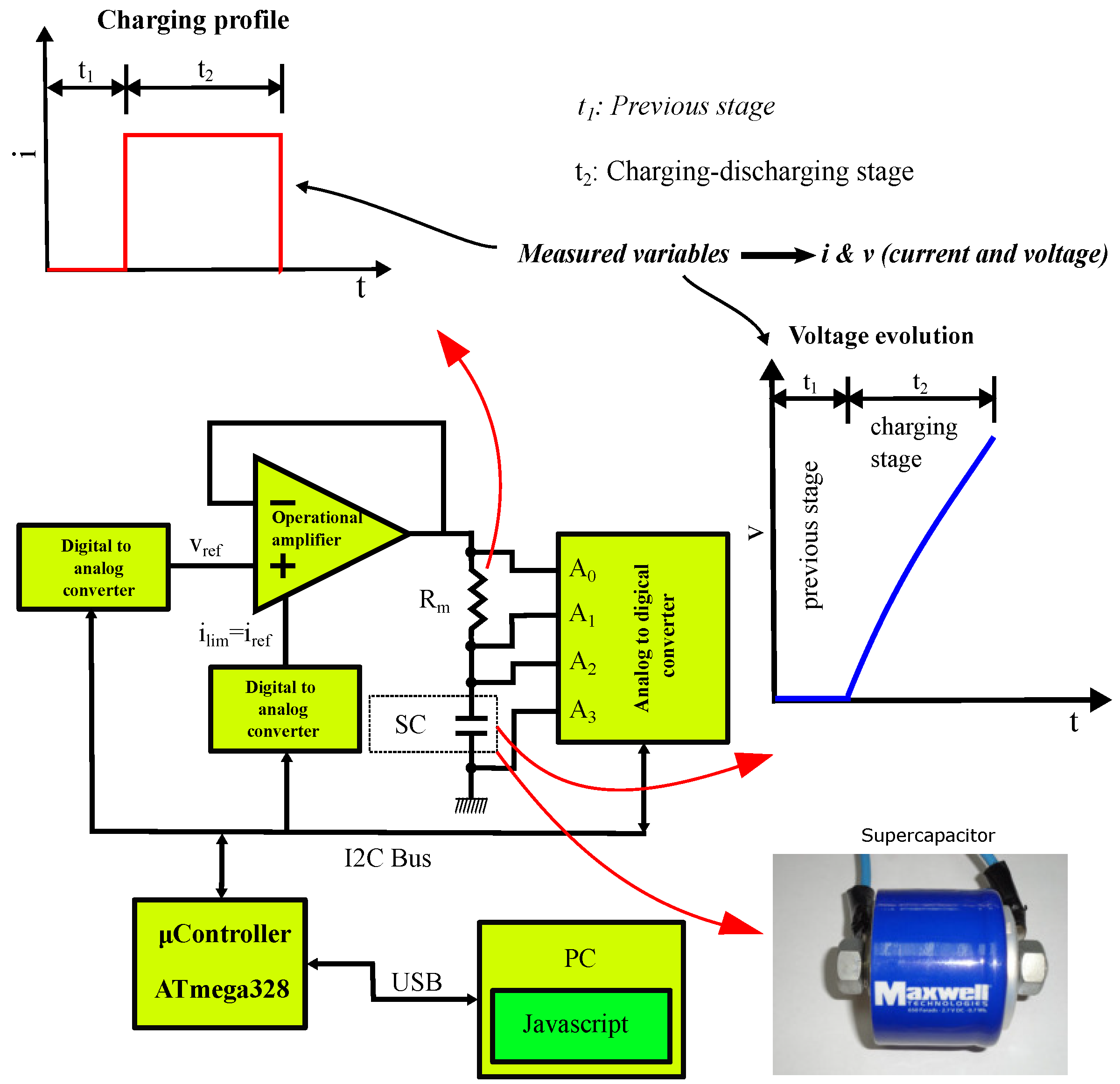
5. Materials and Methods

In order to ascertain the viability of the proposed model, it is necessary to conduct a series of laboratory tests, based on the assumptions made during its construction. This section presents the materials and methods developed in this work, as well as the implementation of the programming codes necessary for the development of the experimentation.

5.1. Materials

Figure 5 illustrates a basic diagram of the experimental design. The system comprises the following elements:

• An operational amplifier OPA549 (Texas Instruments, Dallas, TX, USA). This operational amplifier can provide a nominal current of 8 A, plus it has a special input ($i_{lim}$) to limit the output current of the amplifier. This is an important feature for the implementation of galvanostatic charge and discharge processes by controlling the current.
• An analog-to-digital conversion stage (Figure 6) based on the precision converter ADS1115 (Texas Instruments), which is mounted on a board from Adafruit Industries (New York, NY, USA). This stage has two analogue channels in the differential mode, for the measurement of charge–discharge current and supercapacitor voltage. The current $i\left(t\right)$ is measured from the voltage of a resistor in series with the supercapacitor $R_m=0.1\Omega$, and the voltage is measured directly $v\left(t\right)$. The ADS1115 circuit has a resolution of 16 Bit, giving a resolution of 3 mV for the voltage measurement and 30 mA for the current.
• Two digital-to-analog conversion stages (Figure 7) based on a 12 Bit resolution MCP4725 (Microchip, Chandler, AZ, USA), which are mounted on a board from Adafruit Industries. These stages are used to control the charge–discharge processes of the supercapacitor, and to adjust the voltage and current references.
• A microcontroller model ATmega328 (Microchip) implemented on an embedded system, which is called Arduino Nano (Figure 8). This microcontroller is responsible for controlling the galvanostatic charging and discharging processes, as well as capturing data and sending it, via USB, to the PC to be saved. The microcontroller is responsible for adjusting the output voltage of the two digital-to-analogue converters: the first to set the target voltage to be applied to the output of the operational amplifier, which operates in a voltage follower configuration, and the second digital-to-analogue converter to set the charge or discharge current of the supercapacitor, thus achieving galvanostatic operation of the system. Therefore, by using the indicated devices, it is possible to implement a galvanostat that meets the requirements of the experimental design of this article, without the need for other devices.
• A PC, which is responsible for controlling and configuring the microcontroller for the designed tests, as well as for storing the captured data obtained from the measurements. This is achieved by means of a program implemented in JavaScript language, under the Processing environment, Processing Foundation. This program is an interface to communicate and control the embedded system (Arduino Nano) with the PC. Processing is a flexible, open source, free, cross-platform application. There is a lot of information on the internet for programming on this platform.

Finally, a system photograph is displayed in Figure 9.

5.2. Microcontroller IDE and Interface GUI

This work has used the Arduino IDE to develop and program the microcontroller indicated above, as can be seen in Figure 10. The source code used is shown in Appendix A.

On the other hand, for communication, test management and storage of experimental data, an interface application has been implemented and developed in Processing, an image of which is shown in Figure 11. The source code used is shown in Appendix B. Processing is a flexible software sketchbook and a language for learning how to code. Processing is based on the Java programming language, although it is also possible to code in other languages, including JavaScript, Android, and Python, among others.

6. Results

The following are the charging and discharging tests performed on a 50 F supercapacitor. Figure 12 shows the charging results, applying a constant current of 3 A. The upper curve in Figure 12 shows the actual response of the supercapacitor on a conventional time scale $\tau$, as well as the results from the fractional model. The parameter values for this capacitor are shown in

Table 1. Charging operation parameters.

${\mathit{R}}_{\mathit{\alpha }}$	${\mathit{C}}_{\mathit{\alpha }}$	$\mathit{\alpha }$	Error
$0.1661$	$29.6736$	$0.8575$	$0.00009$

, which have been obtained from the identification process. From these parameters, the following expression obtained from (9) is presented:

$$\begin{array}{c}v\left(t\right)=0+0.1661·3+{\displaystyle \frac{1}{29.6736}}{\displaystyle \frac{3}{\Gamma (1+0.8575)}}{t}^{0.8575}\hfill \\ \\ v\left(t\right)=0.4983+0.1067t^{0.8575}\hfill \end{array}$$

(22)

The results of the fractional model, expression (22), are plotted in Figure 12 together with the experimental results.

In the lower curve of Figure 12, the experimental response is shown with a transformed time scale $g_t\left(\tau \right)$, determined from the identification.

Figure 13 shows the discharge results, applying a constant current of $-3$ A. In the upper curves of the figure, the actual response of the capacitor on the conventional time scale $\tau$ is shown, as well as the results of the fractional model. The parameter values for this discharge process are presented in

Table 2. Discharge operation parameters.

${\mathit{R}}_{\mathit{\beta }}$	${\mathit{C}}_{\mathit{\beta }}$	$\mathit{\beta }$	Error
$0.1997$	$64.9350$	$1.0975$	$0.00024$

. Based on these parameters, the following expression (10) obtained from the table is given:

$$\begin{array}{c}v\left(t\right)=2-0.1997·3-{\displaystyle \frac{1}{64.9350}}{\displaystyle \frac{3}{\Gamma (1+1.0975)}}{t}^{1.0975}\hfill \\ \\ v\left(t\right)=2-0.5991-0.0442t^{1.0975}\hfill \end{array}$$

(23)

The results of the fractional model, expression (23), are plotted in Figure 13, together with the experimental results.

The lower curve in Figure 13 shows the actual response with a transformed time scale $g_t\left(\tau \right)$.

From the results of Table 1 and Table 2, it can be seen that the error of the fit of the data are very small, because the model obtained from the parameters practically coincides with the experimental data (Figure 12 and Figure 13).

7. Conclusions

This paper presents a mathematical model that accurately predicts the dynamic response of electrochemical capacitors to constant current charging and discharging. Furthermore, the effect of employing non-integer integration is elucidated through the use of the Riemann–Liouville integral. It can be concluded that the fractional model fits the data much better than the conventional ($RC$) models.