Abstract
The imbalance cost pass-through (ICPT) is a flexible component of the incentive-based regulation (IBR) that empowers power producers to adjust tariffs in response to variable fuel prices, thereby enhancing the economic resilience of electricity generation. In Malaysia, the Energy Commission has conducted biannual reviews of fuel and other generation costs. Any cost savings or increases identified during these reviews will be passed on to customers in the form of rebates or surcharges. Meanwhile, if an increment in the ICPT price signal can be provided to electricity providers and consumers, early preparation for operation budgeting can be realised, and energy management program development can be properly prepared. Due to this reason, this study proposes ICPT price forecasting for the electricity market in Peninsular Malaysia that will benefit the stakeholders. The study aims to construct an ICPT-related baseline model for the peninsular generation data by employing three forecasting methods. The forecasting performance is analysed using the mean absolute percentage error (MAPE). In light of our findings, the ARIMA method is one of the most accurate forecasting methods for fuel prices compared to the moving average (MA) and LSSVM methods. The observed price differences between the ARIMA and LSSVM models for ICPT are minimal. The ICPT price for July–December 2022 and January–June 2023 is MYR 0.21/kWh for the ARIMA and MYR 0.18/kWh for LSSVM, which are close to the actual TNB’s ICPT tariff. As for forecasting, the ICPT price is expected to drop in the next announcement. The findings of this study may have a positive impact on the sustainability of the energy sector in Malaysia.
1. Introduction
Malaysian Electricity Supply Industry (MESI) 1.0, which took place from 2010 to 2014, was approved by the government in 2009. The objectives were to improve the tariff mechanism, fuel supply, and security, and to achieve effective governance in power sector management. The ring-fenced, single-buyer model was established due to those initiatives [1]. Additionally, the single-buyer (SB) and grid system operator (GSO) divisions joined the MESI following their separation from Tenaga National Berhad (TNB). In 2015, the Energy Commission launched the New Enhanced Dispatched Agreement (NEDA) to provide an opportunity for the power sector to increase its efficiency and be more cost-effective in generating electricity. This new method can reduce power production costs while benefiting consumers in the long run. The NEDA regime has implemented short-run competition in generating dispatch daily among Independent Power Producers (IPPs) with Power Purchase Agreements (PPAs), TNB generation with Service Level Agreements (SLAs), and merchant generators without PPAs. All generation players are required to use the System Marginal Price (SMP). The introduction of the MESI and NEDA has resulted in some positive industry impacts. Still, more effort is needed to keep tariffs as stable as possible, while the efficiency of power generation system operations needs to be improved to protect against exposure to fuel price volatility.
Thus, in 2018, MESI 2.0 was introduced with the core idea of redesigning MESI 1.0 [2]. The MESI 2.0 reform aimed to make the electricity market more effective by making it more efficient, transparent, sustainable, and competitive [3]. In addition to managing Power Purchase Agreements (PPAs) and settlements, the SB department oversees least-cost dispatch scheduling, managing the forecasting of electricity demand, and planning generation capacity, whereas the Energy Commission (EC) is entrusted explicitly with acquiring additional generation capacity identified previously by the SB [4]. In all cases, power plants will sell energy to the SB at the PPA pricing. The producing company will be compensated in two ways: the capacity payment and the energy payment [5]. Moreover, the GSO is a ring-fenced department within TNB accountable for the operational planning, real-time rescheduling, dispatch, and management of the grid system following grid code requirements. The GSO is also responsible for coordinating all parties involved in the grid system, including electricity generation, transmission, and distribution networks across multiple countries or continents [6].
However, fuel and generating expenses have increased to around 70% of the overall tariff costs paid by consumers, with the remaining 30% made up of operations and maintenance costs [7]. TNB and the government cannot prevent changes in electricity tariffs because the adjustment depends on global fuel price changes, including coal and natural gas prices. Around 70% of Malaysia’s coal is bought from Indonesia, and the remaining is imported from Australia, South Africa, and Russia [8]. Due to this reason, MESI reform initiatives began introducing an incentive-based regulation (IBR), which consists of two types of fundamental tariff, (a) a base tariff and (b) the imbalance cost pass-through (ICPT) mechanism, which has helped keep electricity tariffs stable through Malaysia’s single-buyer model. The base tariff was set at 39.45 cents/kWh and has remained the same price up to the present. For instance, if coal cost USD 87.50 (MYR 337.3)/ton, LNG would cost MYR 41.68/mmBtu, and regulated gas would cost MYR 15.20/mmBtu. The Energy Commission (EC) continues to audit and review past performance while accommodating new utility company requests. The utility must provide its expected revenue requirement for the next three to four years based on forecasted capital expenditure (CAPEX), operational expenditure (OPEX), and expected return. The three to four years is known as a regulatory period (RP), during which the utility must operate within the allowed CAPEX and OPEX to deliver the required service. The cost of coal was about MYR 250 per metric ton when the ICPT was introduced. The cost of coal had risen to more than MYR 370 per metric ton by the beginning of 2018 [9], a 47% increase in price. Since the ICPT price depends on the fuel price and other generation costs, the Energy Commission will conduct biannual reviews with any cost savings or increases identified during these reviews will be passed on to customers in the form of rebates or surcharges. The ICPT charge on electricity bills differs for each consumer, as the ICPT charge is based on the monthly energy consumption (kWh) [10]. Thus, Figure 1 illustrates the complexity of the MESI in Peninsular Malaysia, where the integrity and transparency of the electricity market have been set as main objectives for the framework design.
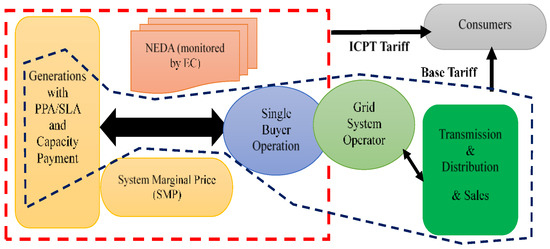
Figure 1.
The general description of the MESI structure in Peninsular Malaysia comes with two types of tariffs, which are the ICPT and the base tariff, under the IBR.
Unfortunately, the ICPT forecast charges are not made publicly available, which creates a crucial need to provide consumers such as large commercial and industrial businesses with an ICPT forecasting mechanism so that they are able to manage their energy consumption and operations cost-efficiently. Hence, in this study, forecasting models are introduced based on the time series (moving average), the ARIMA model, and the LSSVM, which represent the most popular techniques used in the literature. These are explained in detail in the following section. The contributions that this paper makes to this topic are as follows:
- (1)
- It presents a novel forecasting formulation model for the ICPT regime in Malaysia, where the accuracy of the model has been configured and tested with time series and machine learning techniques.
- (2)
- It provides a comprehensive analysis of the data collected from the real generation system while putting forward much widespread discussion on the three-baseline model for the ICPT’s main component.
- (3)
- It contributes to providing valuable forecasting ICPT price information for electricity consumers in Peninsular Malaysia, where the sustainable electricity market can be enhanced significantly.
The remainder of the paper is organised as follows: In Section 2, the related previous work on forecasting models is introduced. In Section 3, the formulation of the ICPT based on the IBR regime is explained, while Section 4 demonstrates the implementation of the forecasting methods. Section 5 discusses the findings, and the last conclusion section will be Section 6.
2. Related Previous Work on Forecasting Models
The ARIMA forecasting model is the most common type of linear time series model, based on the Box–Jenkins methodology, as presented in [11]. In most cases, this methodology does not require the estimation of many parameters to make the final choice of model [12]. As an adaptation of this model, the authors in [13] applied it for the short-term forecasting of Spanish day-ahead electricity market prices. Meanwhile, using the Reference Price Data (RPD) from the UK energy market, the authors in [14] described and analysed the ARIMA and ANN models for predicting the price of electricity up to three steps (1.5 h) ahead. Based on the root-mean-square error (RMSE), the results show that the ARIMA (4,1,2) model was more accurate when compared to the ANN model. Hence, the application of the ARIMA model was used to investigate the USD-per-day price of gold during short-term and long-term periods [15]. It is observed that the ARIMA is deemed the most effective for predicting gold USD prices and in other related electricity pricing forecasting, as explained in [8]. On the other hand, the well-known statistical test of the analysis of variance (ANOVA) was conducted in [16,17] for forecasting electricity prices one day ahead, based on the best possible synthesis of a few univariate and multivariate approaches. Even though the ANN model was less accurate, the improvement model was able to predict better, as explained in [14], where the application of it in predicting long-term oil and real-time electricity prices was able to fulfil the standard accuracy percentage, as shown in [18,19]. Aside from the time series forecasting method, the machine learning method has been applied in various fields, including the electricity market. The studies in [20,21] explore the application of a hybrid forecasting model known as Grey Wolf Optimizer–Least-Squares Support Vector Machines (GWO-LSSVMs) in the context of price prediction. The authors of [22,23] propose a novel method for forecasting electricity prices that combines clustering and Least-Squares Support Vector Machines (LSSVMs). A methodology has been proposed that combines the advantages of clustering and LSSVMs to improve the precision of electricity price forecasts. These advancements are crucial for consumers to manage energy consumption and operations cost-efficiently [24,25].
In the context of Malaysia, the application of the forecasting method in the electricity market has been explored and discussed in various studies. These studies have focused on developing more accurate and efficient forecasting models rather than considering the ICPT charge. Hence, to the best of our knowledge, there are no presented findings that have been published in a past study to discuss ICPT predictions for the IBR regime in Malaysia. Even though Asian countries may have different electricity markets, the formulation of the ICPT in this study can help them to manage a single-buyer-based market, where the southern ASEAN countries are able to enhance their generation market too. Therefore, the findings of this study contribute significantly to the body of knowledge since they provide a method of forecasting ICPT pricing. Electricity consumers can use this information to make more informed decisions regarding their energy consumption. The findings of the study may also help empower consumers to become more aware of the volatility of ICPT costs. These data can assist consumers in making more informed financial decisions about their energy consumption and operation costs. Thus, this paper aims to establish a baseline model for the peninsular generation data while comparing the performance through the mean absolute percentage error (MAPE) of the time series forecasting (moving average), ARIMA, and Least-Square Support Vector Machine (LSSVM) techniques. Meanwhile, at the end of the study, the ICPT price prediction for Peninsular Malaysia under the IBR regime is proposed congruently.
3. Formulation of ICPT
The single-buyer tariff has two components: (1) the Single-Buyer Generation, which accounts for all generation costs, including fuel, capacity payments, and other expenses related to the terms and conditions of PPAs, SLAs, and other fuel procurement contracts, and (2) the SBO component, which accounts for all other operational and capital costs associated with SB operations and allocates joint costs (if any). The SB will forecast the generation cost for the generation-specific component using the current gas and coal prices. The profitability of the generation utility may be impacted by the extremely volatile nature of fuel prices. Therefore, an adjustment to the fuel price is permitted to protect the TNB from this inconsistency. The ICPT is made up of two parts: the fuel cost pass-through (FCPT) accounts for changes in gas and coal costs due to changes in fuel prices, availability, foreign exchange rates, etc., and the generation-specific cost pass-through (GSCPT) accounts for changes in other fuels (such as distillate and medium fuel oil (MFO)) and all costs incurred by the single buyer under PPAs and SLAs (incentive or bonus payments, liquidated damages, savings, etc.). Figure 2 describes the components considered for the ICPT tariff.
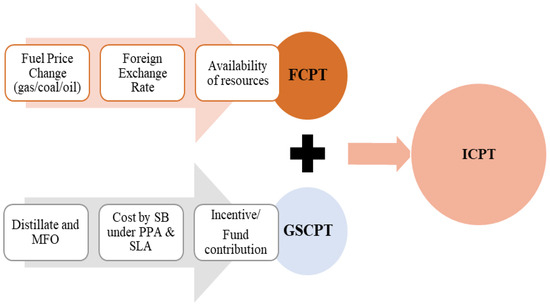
Figure 2.
Considered ICPT components under IBR.
Every six months, the SB will evaluate the generation-specific component of its actual revenue against the cost of electricity acquisition. The SB will have to provide a thorough analysis and supporting evidence to prove the fuel price changes. Customers will be informed of any over or under abundance of the actual figure within the ensuing six months by the government through the Energy Commission.
The formulation of the electricity tariff in Malaysia has adopted ) the incentive-based regulation (IBR), as shown in Equation (1):
where is the base tariff and is the imbalanced cost pass-through (ICPT). Meanwhile, the ICPT has two components, which are the generation cost adjustment for the six-month period (cent/kWh) ( and the fund contribution for the six-month period (cent/kWh) ( as described in Equation (2).
For Part 1 of Equation (2), the details of can be expressed by the following equations:
where A is the first fuel cost pass-through adjustment in the six-month period (cent/kWh). IFUCs is the interim fuel cost pass-through adjustment for the six-month period (cent/kWh). AFULP is the average fuel cost for regulatory period ‘P’ (cent/kWh). Meanwhile, m represents the month in which the ICPT adjustment takes effect; Cm is the estimated total fuel cost for month ‘m’ (MYR); Dm is the actual total fuel cost for month ‘m’ (MYR); Fm is the estimated total qualifying sales (kWh); and Em is the audited total qualifying sales for month ‘m’ (kWh). FFULS is the forecasted fuel cost for the six-month period ‘s’ (MYR); WACCP is the allowed weighted average cost of the capital of RBE for the regulatory period ‘P’ (%); and FSALt is the forecasted total electricity sales in the year ‘t’ as made at the time of setting the base average tariff (in kWh).
On the other hand, B is the first other generation cost pass-through adjustment in the six-month period ‘s’ (cent/kWh). In conjunction with the interim of the other generation cost past-through adjustment, the symbol IGSCS demonstrates the six-month period ‘s’ (cent/kWh). AGSCP is the average other generation cost for the regulatory period ‘P’ (cent/kWh) that finally contributes to the second fuel cost and other generation costs’ pass-through adjustment in the six-month period (cent/kWh), A1 and B1, congruently. Meanwhile, Gm and Hm represent the estimated total other generation cost for month m (MYR) and the actual total other generation cost for month m (MYR), respectively. On the other hand, for Part 2 of Equation (2), the details of can be expressed by the following Equation (12):
where FUNTm is an approved payment from the Electricity Industry Fund (EIF) to the single buyer, related to the ICPT adjustment, for month m (MYR), while FUNPm is the payment by the single buyer into the EIF, related to the ICPT adjustment for month m (MYR). The calculation result was divided to estimated the total qualifying sales (kWh), Fm, accordingly. Basically, the value of Fx was considered fixed during the adjustment but really depends on the banking announcement, especially on the overnight policy rate (OPR) values.
Since introducing the ICPT mechanism, consumers have received rebates worth MYR 6.3 billion [3]. By successfully implementing sixteen (16) ICPT cycles since 2015, the government has protected MYR 11.7 billion from the effects of rising fuel prices. This includes the most recent MYR 5.8 billion in subsidies for the ICPT implementation period of July to December 2022. In addition, all Peninsular Malaysia consumers received an MYR 9.35 billion ICPT cost rebate from the government. The average price of coal has risen dramatically, which has led to this ICPT surcharge. Since coal is used for 59% of Peninsular Malaysia’s generation, the increase in coal prices between January 2022 and June 2022 has significantly impacted its overall cost of generation [15]. From 1 July until 31 December 2022, all residential customers received their current rebate of 2.00 cent/kWh. However, from 1 February 2019 to 30 June 2022, all nondomestic customers were subjected to an ICPT surcharge of 3.70 cent/kWh. The details of the ICPT tariff are illustrated in Figure 3 (the green colour indicates a rebate, while the red colour indicates surcharge). Since July 2023, the surcharge for commercial and industrial consumers has been increased to 20 cents/kWh.

Figure 3.
Previous ICPT price.
4. Method
4.1. Forecasting Formulation
The formulation of those forecasting methods with the objective function of the MAPE is presented in the Equations (13)–(19), respectively. However, for the ARIMA model, the equation contains three terms:
- (1)
- Autoregression (AR): A regression analysis is used to compare the time series to its prior values, such as y(t − 1), y(t − 2), etc. The letter p stands for the lag order.
- (2)
- Integration (I): Differencing is used to make the time series stationary. The difference’s order is indicated by the letter d.
- (3)
- Moving average (MA): Regression is performed on the time series using residuals from previous observations, such as the error ε(t−1), the error ε(t−2), etc. The error lag order is indicated by the letter q. In the equation above, y^′ is the differenced series, ϕ1 is the first AR term’s coefficient, p is the AR term’s order, θ11 is the first MA term’s coefficient, q is the MA term’s order, and εt is the error.
The performance evaluation of the MA, ARIMA, and LSSVM models was conducted using the mean absolute percentage error (MAPE). The MAPE is frequently used to display the error percentage of a prediction result, as shown in Equation (19).
MA:
ARIMA:
MAPE:
where is a kernal weight, is a seasonal component, is the moving average, is a seasonal component, is an irregular component, and is a trend component. Meanwhile, FS is the LSSVM output, b is the scalar threshold, N is the number of data points, and X(norm) is the data normalisation.
4.2. Dataset Collection
The dataset utilised in this study comprises fuel price data for coal, gas, and LNG. The objective is to employ this dataset to forecast fuel prices for a three-year period. The dataset utilised for modelling and model validation spans from January 2012 to December 2022. The data were acquired from the Energy Commission and online sources pertaining to fuel prices. In this study, the modelling techniques of the MA, the ARIMA, and LSSVMs were employed to forecast three-year out-of-sample data points for the purpose of calculating the ICPT price. This section provides a comprehensive overview of the implementation process for fuel price forecasting. There are many available methods in the relevant literature for price forecasting. The most common models for this purpose are the autoregressive integrated moving average (ARIMA) and LSSVM models.
4.3. Implementation of Techniques
The standard procedure for fuel price forecasting using the MA method is illustrated in Figure 4. The flowchart illustrates the procedure for time series forecasting using the MA method in Microsoft Excel. The forecasting process commenced by gathering historical data. The primary data utilised for forecasting fuel prices include coal, LNG, and gas prices. The data are subsequently visualised during the preprocessing stage. Consequently, the data appear to be random or irregular in nature. The MA was utilised as a data preparation technique due to its ability to decrease random variation in observations and reveal more accurately the structure of the underlying causal processes. The calculation involves determining the average of the most recent 12 data points. The smoothness of the trend cycle prediction is determined by the order of the moving average (MA). The subsequent phase involves identifying the seasonal component. The data are subsequently subjected to a process of di-seasonalization in order to eliminate irregularities and seasonal patterns. This is achieved by dividing the actual data by the seasonal value. The application of simple linear regression is subsequently employed to identify the trend component, which is then utilised for forecasting the future price of fuel. When evaluating the model outputs that were acquired, the mean absolute percentage error (MAPE) for the time series model was employed as an evaluation criterion.
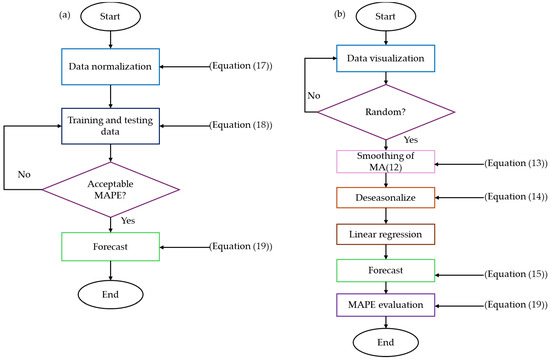
Figure 4.
Flowchart of (a) LLSVM and (b) moving average processes.
Differently from the MA, the goal of the LSSVM algorithm is to locate the hyperplane that best separates or fits the data that have been provided for training. To learn the underlying patterns and relationships that exist between input variables and output variables (forecasted), the LSSVM makes use of past data. After that, it builds a model that, based on the observed patterns in the training data, can be utilised to make accurate predictions regarding future values. The process of prediction using the LSSVM approach is illustrated in Figure 4.
It is necessary to perform the necessary preprocessing on the historical data pertaining to fuel prices in order to train the LSSVM model. After they have been collected, the data must undergo preprocessing, during which any outliers or inconsistencies must be resolved. In order to guarantee that the data are presented in a format that is suitable for the LSSVM method, the data must first be normalised. Data normalisation was conducted prior to training by employing min–max normalisation, a technique that normalises each feature component to a specific range [26]. This ensures that larger input values do not overpower or overshadow the smaller ones. Following that step, the dataset was segmented into a training set and a testing set. The LSSVM model was trained using the training set, and the testing set was used to evaluate the model’s performance in terms of prediction. The whole dataset of 132 sample points for coal, gas, and LNG was split into two subsets: (a) the training dataset, which includes 84 sample points necessary for training the model, and (b) the testing dataset, which includes 48 sample points to evaluate the performance of a model. There is a distinction in performance between the LSSVM when being tested and when being trained. Because of overtraining, an LSSVM typically displays superior performance during the training phase as compared to the testing phase. Training for the LSSVM model was carried out with the help of historical data. The LSSVM method determines which hyperplane is the most accurate prediction based on the training data and then optimises that hyperplane. The strategy of least squares was used to solve a constrained optimisation issue, which enables this result to be obtained. After the model was trained, its performance was evaluated using the MAPE [27]. The LSSVM model that was trained was given the input variables for the upcoming time periods, and the model then gave forecasts for the years 2023, 2024, and 2025.
On the other hand, the ARIMA model took the historical data and divided it into three components: autoregression (AR), which shows a changing variable regress on its own lag; integration (I), which represents linear or polynomial trends; and the moving average (MA), which represents the dependency between the observation and residual error. As a result, the model has three model parameters: AR(p), I(d), and MA(q), which are all combined to form the ARIMA (p, d, q) model parameters, AR(p), I(d), and MA(q), where p is the autocorrelation order (lag), d is the differencing order, and q is the moving average order.
The ARIMA model attempts to ensure that the future values of time series data have a practical connection to the current and historical values. ARIMA model building consists of four major steps, which are identification, estimation, diagnostics, and forecasting [28]. With the help of these four steps, the tentative model parameters are first identified using graphs of the autocorrelation function (ACF) and partial autocorrelation function (PACF), after which the coefficient is calculated and the likelihood model is determined. The model must then be validated, and to assess the forecast’s veracity and monitor the model’s performance, simple statistics were applied. The time series must be stationary before using the ARIMA or any of its extensions. If a time series possesses all three of the following characteristics, which are a constant mean, variance, and covariance, it is said to be stationary. There are two methods to check for stationarity, which are (i) autocorrelation to check the stationary criteria and (ii) autocorrelation to check the stationarity criteria.
Based on the analysis of Figure 5, Figure 6 and Figure 7, it can be observed that the autocorrelation function (ACF) for coal, gas, and LNG exhibits a positive value with a consistent and gradual decrease over time. The lagging issues extend beyond the designated blue-highlighted area. This suggests that there is a lack of zero correlation between observations at different lags for all fuel types. The presence of additional spikes beyond the blue range indicates that the series does not exhibit characteristics of ‘White Noise’. An illustration of a stationary time series is the phenomenon known as ‘White Noise’. Based on the analysis, it can be inferred that the time series data for coal, LNG, and regulated gas exhibit nonstationarity.
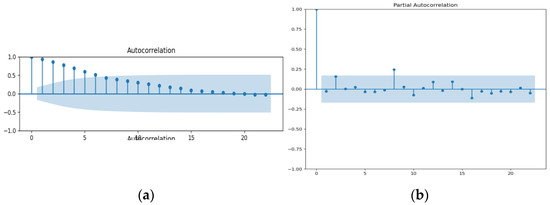
Figure 5.
(a) ACF and (b) PACF of coal.
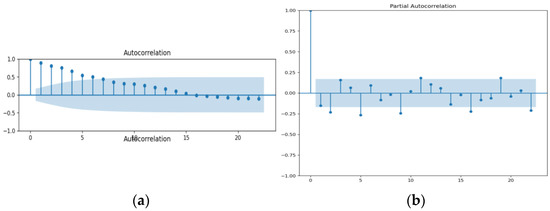
Figure 6.
(a) ACF and (b) PACF of gas.
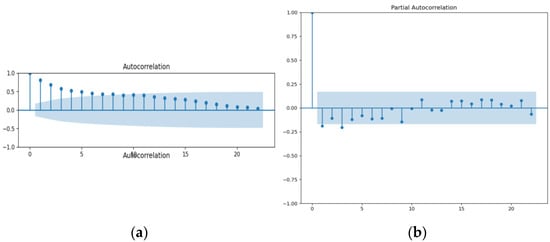
Figure 7.
(a) ACF and (b) PACF of LNG.
Another method for assessing stationarity is the augmented Dickey–Fuller test (ADF test). This statistical test belongs to the subcategory of unit root tests. This analysis aims to determine the presence of nonstationarity and the existence of a unit root in the time series. The assumptions are as follows: (a) the null hypothesis, Ho, is that the time series is nonstationary and has a unit root, and (b) the alternate hypothesis, H1, is that the time series is stationary and has no unit root.
The ADF assessment was carried out using the original dataset. The p-value from the ADF test is 0.951480 for coal and 0.267107 for gas, both of which are greater than 0.05. At 5% significance, the null hypothesis cannot be rejected. As a result, the test does not reject the null hypothesis. According to the ADF test, the series has a unit root and is nonstationary. The p-value for LNG is 0.012868, which is less than 0.05. As a result, the null hypothesis was rejected, and the series was determined to be stationary. The differential test was carried out on nonstationary data, and the smoothness of the data was then assessed using the ADF test. The d-value in the ARIMA (p, d, q) model was chosen after passing the stationary test [29]. The next step was to identify a suitable model. The p and q values of the ARIMA model must be determined. Using the auto-ARIMA function to examine the range of the best model, the values of p and q were obtained by observing the sample’s autocorrelation function (ACF) and partial autocorrelation function (PACF). For coal, LNG, and gas, the selected ARIMA models were (1,1,1), (1,0,1), and (2,0,1). An autoregressive order of one for coal and LNG and an autoregressive order of two for gas were used to specify the value of the series one and two time periods in the past to be used to predict the current value. Predictions were made and compared with the testing dataset to validate the model after fitting the input data with a suitable ARIMA model.
Thus, the imbalance cost pass-through (ICPT) is a mechanism employed to transfer the expenses associated with fuel and other generation-related costs to consumers of electricity. The ICPT, or the imbalance cost pass-through, is assessed biannually to determine whether a rebate or a surcharge is applicable. This determination is based on a comparison between the actual fuel costs and the scheduled fuel costs. The ICPT is typically calculated on a semi-annual basis. The adjustment for each type of cost is divided into two components. The initial segment utilises the current data for the two most recent months that are available, along with estimated data for the subsequent four months. The second part corrects for differences between actual outcomes and the estimated data used to calculate the first adjustment. The process for calculating the ICPT for commercial customers involves the following steps:
- (1)
- The initial step in calculating the ICPT involves determining the interim fuel cost pass through adjusting for a six-month period (IFUCS) using Equation (6). The estimated and actual total fuel costs (Cm, Dm) were derived from the projected fuel cost using the ARIMA and LSSVM models. The data for Dm were not accessible due to limited resources. As a result, forecasted data were utilised instead. The estimated total qualifying sales (Fm) were acquired from the websites of single buyers (SBs). The audited total qualifying sales, to which the ICPT adjustment was applied, were obtained from the Grid System Operator (GSO) website. By using Equation (5), the average fuel cost was calculated. The total forecasted fuel cost (FFULs) for six months was derived from the previously forecasted fuel cost. The weighted average cost of capital for Regulatory Period 3 (RP3) was set by the government at 7.3%. The forecasted total electricity sales in the year 2021 as made at the time of setting the base average tariff were obtained from the SBs.
- (2)
- Then, using Equation (6), the first fuel cost pass-through adjustment (As) was determined.
- (3)
- Next, Equation (7) was used to determine the interim of the other generation cost pass-through adjustment (IGSCs). System marginal pricing (SMP) on SB websites was used to determine the estimated and actual total other generation costs (Gm, Hm).
- (4)
- To determine the average other generation cost (AGSCs) using Equation (8), the forecasted other generation cost was obtained by subtracting the generation margin (Gm) from the forecasted fuel and fuel-related costs (FFULs).
- (5)
- Equation (7) is then used to compute the first other generation cost pass-through adjustment (Bs) in the six-month period.
- (6)
- The next part involves calculating the secondary fuel and additional generation cost pass-through adjustment within the designated six-month timeframe. This can be achieved by utilising Equations (10) and (11).
- (7)
- The remuneration rates for the ICPT adjustment, specifically IARRs-1 and IARRs-2, are constantly set at 2.8738 and 2.86, respectively.
- (8)
- The six-month generation cost adjustment was determined using Equation (3).
- (9)
- Equation (12) was used to compute the fund contribution (FUNDs). The approved payment (FUNPm) from the Electricity Industry Fund (EIF) and the payment by the single buyer (FUNTm) into the EIF are fixed at MYR 1.6 billion and MYR 1.3 billion, respectively.
- (10)
- The ICPT price was then determined using Equation (2).
Even though the ICPT is a controversial mechanism, it is still an important part of the electricity market. The ICPT helps to ensure that consumers pay the true cost of electricity, and it can help to protect consumers from large fluctuations in fuel prices. Thus, the summary of the method process flow for finding the forecasted ICPT is demonstrated in Figure 8 congruently.
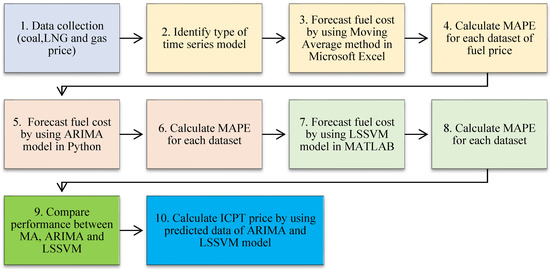
Figure 8.
Summary study flow to obtain the best value of ICPT forecasting.
5. Results and Discussion
This section presents an analysis of different fuel price forecasting methods, specifically the implementation of the MA, ARIMA, and LSSVM models. Meanwhile, in Figure 9, a correlation heatmap using Pearson correlation is presented to show the significant relationship between the three variable prices of fuel types compared to the ICPT price. It is observed that even though the correlation coal price is moderate compared to the ICPT price, the value of the regression still significantly reflects the standard Pearson range, as shown in Table 1.
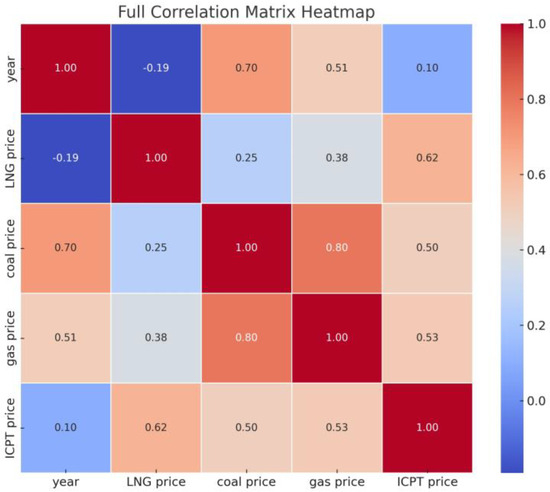
Figure 9.
Correlation heatmap using Pearson’s regression technique.

Table 1.
Descriptive conditions based on Pearson’s correlation method.
This section also covers an analysis of the MAPE for the different forecasting methods and the implementation of the ARIMA and LSSVM models in estimating the ICPT price for commercial customers.
5.1. Moving Average (MA) Forecasting Profile
One approach to predicting fuel prices is through the implementation of the moving average method. The data are smoothed by calculating the average of 12 data points, as depicted in Figure 10a–c. The moving average method for predicting fuel prices has proven to be unreliable. For coal, the actual price in January 2012 was MYR 9.18/mmBtu, nearly double the predicted MYR 4.50/mmBtu. This trend of significant differences continued until December 2022. For gas, the predicted price in January 2012 was MYR 8.65/mmBtu, slightly higher than the actual MYR 7.78/mmBtu. The largest discrepancy was in August 2022, with the actual price being MYR 40.71/mmBtu, more than double the predicted MYR 17.74/mmBtu. For LNG, the predicted price in January 2012 was MYR 37.05/mmBtu, slightly higher than the actual MYR 35.9/mmBtu. The largest difference was in November 2015, with the actual price being MYR 69.89/mmBtu, more than double the predicted MYR 30.95/mmBtu.
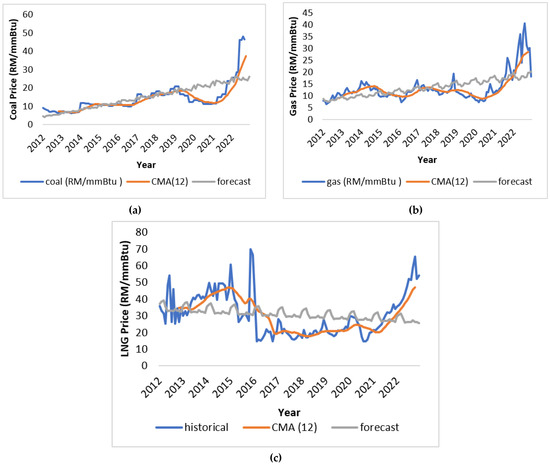
Figure 10.
MA fuel price forecasting: (a) coal price; (b) gas price; and (c) LNG price.
5.2. LSSVM Forecasting Profile
The LSSVM forecasting method, as depicted in Figure 11a–c, shows significant disparities between the predicted and actual prices. In the coal market (Figure 11a), the January 2022 prediction of MYR 13.55/mmBtu was notably lower than the actual MYR 25.53/mmBtu, with this trend persisting until December 2022. The actual coal price reached MYR 44.62/mmBtu, whereas the prediction was only RM 16.26/mmBtu, resulting in a substantial MYR 28.36 difference. These findings cast doubt on the reliability of the LSSVM model for coal price forecasting. Figure 11b presents gas price variations, mirroring the coal market’s discrepancy. In January 2022, the actual gas price was MYR 20.71/mmBtu, contrasting with the predicted MYR 10.76/mmBtu, a 9.95/mmBtu difference. May 2022 saw a substantial gap, with the actual price at MYR 36.05/mmBtu and the predicted price at MYR 10.8/mmBtu. Figure 11c illustrates the LNG prices, with the January 2022 predictions surpassing the actual prices by MYR 0.88/mmBtu. The actual prices then surged, reaching MYR 36.42 in February 2022, while the predictions stood at MYR 22.23/mmBtu. October 2022 saw a significant spike to MYR 65.47/mmBtu, far exceeding the predicted MYR 25.50/mmBtu, resulting in a MYR 39.97 difference. By December 2022, the predicted price was MYR 43.09, but the actual price was MYR 54.23.
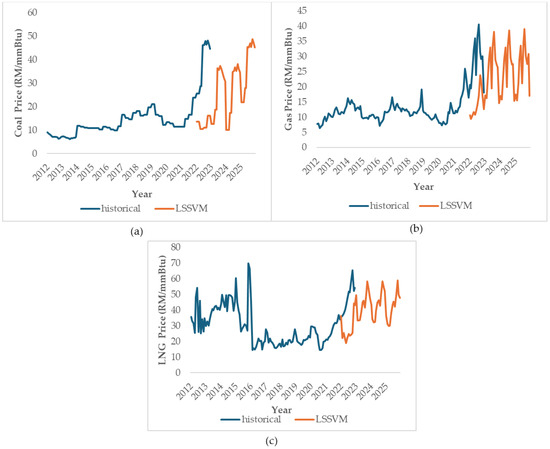
Figure 11.
LSSVM fuel price forecasting: (a) coal price; (b) gas price; and (c) LNG price.
5.3. ARIMA Forecasting Profile
The second method of forecasting involves the implementation of the ARIMA model. According to Figure 12a–c, the forecasted fuel prices are closely aligned with the actual trend. The coal price predictions closely matched the actual prices, with minor deviations starting in February 2012. For example, in December 2012, the forecasted gas price was MYR 7.18/mmBtu, nearly matching the actual price of MYR 7.21/mmBtu. However, in March 2019, a slight overestimation occurred, with a predicted price of MYR 21.13/mmBtu compared to an actual price of MYR 20.99/mmBtu. The forecast for December 2022 closely aligned with the actual MYR 44.62/mmBtu. Gas prices showed discrepancies between the predictions and the actual outcomes. From January 2012 to November 2013, the predicted prices consistently exceeded the actual values. Notably, in January 2012, the actual gas price was MYR 7.78/mmBtu, while the prediction for November 2013 reached MYR 12.64/mmBtu. The highest recorded gas price in August 2022 was MYR 40.71/mmBtu, whereas the prediction was MYR 37.66/mmBtu. The LNG price predictions exhibited disparities, with occasional overestimations and underestimations compared to actual prices. In January 2022, the actual price stood at MYR 35.9/mmBtu, slightly higher than the predicted MYR 35.24/mmBtu. Predictions began at MYR 28.67/mmBtu in May 2015, peaking at MYR 35.68/mmBtu in November 2021. However, the predictions fell below the actual prices afterwards. December 2022 presents an actual price of MYR 54.23/mmBtu, while the expected price settled at MYR 50.87/mmBtu.
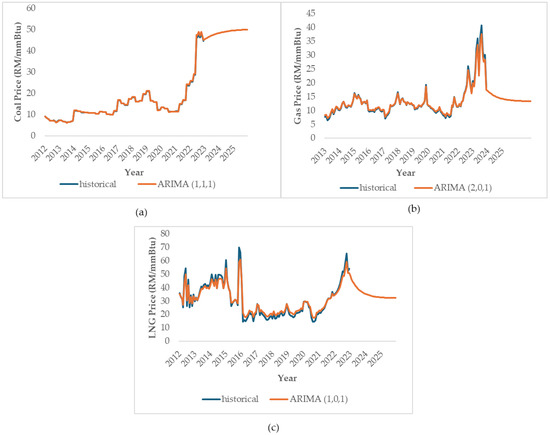
Figure 12.
ARIMA fuel price forecasting: (a) coal price; (b) gas price; and (c) LNG price.
5.4. Analysis of the MAPE
The performance of the MA, LSSVM, and ARIMA models in prediction is presented in Table 2. The ARIMA model demonstrated superior performance compared to the MA and LSSVM models. As the forecast horizon extends, the predictive accuracy of both the MA and ARIMA models diminishes. The findings suggest a decrease in error (MAPE) and an improvement in prediction accuracy when utilising the ARIMA model. The mean absolute percentage error (MAPE) value obtained from the ARIMA model for coal is 1.63%. This is in contrast to the MA value of 29.79% and the LSSVM value of 26.28%. The MAPE values for the gas dataset are 32.94%, 5.47%, and 34.46% for the MA, ARIMA, and LSSVM models, respectively. The ARIMA model demonstrates the lowest error percentage at 5.09% in comparison to the MA model with an error percentage of 39.78% and the LSSVM model with an error of 36.9%.

Table 2.
Comparison of the MAPE for price forecasting methods.
Based on the observed trend, it can be concluded that the ARIMA model outperforms both the MA and LSSVM models in the current case. This conclusion is drawn from the fact that the relative error of the model prediction increases as the forecast period extends. The ARIMA model demonstrated superior performance compared to the LSSVM model, potentially attributed to the limited amount of data available to train the LSSVM model. The limitations of the ARIMA model lie in its ability to predict fuel prices solely based on its own time series data. Consequently, the model’s validity is contingent upon the absence of significant changes in the external factors that influence fuel prices. The analysis and forecasting of fuel pricing, specifically coal, gas, and LNG, are influenced by a range of factors [30]. These factors include supply and demand dynamics, currency exchange rates, regulatory frameworks, and international political situations. Furthermore, these factors exhibit interdependencies and exert a substantial influence on fuel expenditure.
5.5. Discussion of the Forecast ICPT
The prices of the ICPT were measured using the ARIMA and LSSVM forecasting models because these two models have minimal MAPE values. A smaller MAPE value indicates a more accurate model. The ARIMA model is slightly more accurate than the LSSVM model in the present case. The ICPT pricing for commercial customers in Malaysia is displayed in Figure 13 for the period spanning July–December 2022 through January–June 2024, as predicted by the ARIMA and LSSVM models. Both the ARIMA and LSSVM models predict that the ICPT price will decline in 2024. From July 2022 to June 2023, according to the ARIMA forecast, the ICPT tariff for commercial customers is anticipated to remain unchanged at MYR 0.21/kWh. This price is roughly the same as the price determined by the Energy Commission at MYR 0.20/kWh. The ICPT price is anticipated to increase to MYR 0.23/kWh in July–December 2023. According to the LSSVM forecast, the ICPT price will increase from MYR 0.18/kWh in July–December 2022 to MYR 0.21/kWh in July–December 2023.
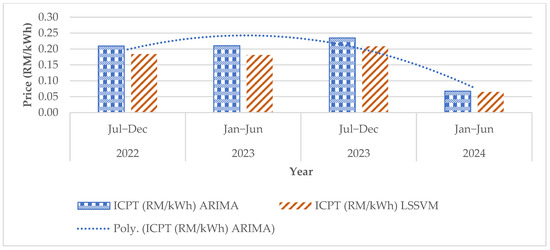
Figure 13.
ICPT price for commercial customer.
The anticipated ICPT for July–December 2023, however, is not close to the government-set ICPT price of MYR 0.17/kWh. This is partly due to the limited number of resources used in determining the ICPT price. According to the ARIMA and LSSVM forecasts, the ICPT price is expected to decline in 2024. In January–June 2024, the ARIMA forecast predicts the ICPT surcharge price will decrease to MYR 0.07/kWh, while the LSSVM forecast predicts the ICPT surcharge price will decrease to MYR 0.06/kWh. A number of factors, which include the continuous decline in fuel prices and the government’s efforts to reduce the cost of energy for consumers, are predicted to contribute to the ICPT price decline in 2024. In the upcoming years, the ICPT price for commercial customers is anticipated to fluctuate. As the government continues to intervene in the energy market and implement policies to reduce fuel prices, the long-term trend is anticipated to be downward.
6. Conclusions
In conclusion, this study introduces imbalance cost pass-through (ICPT) price forecasting as a critical tool within Malaysia’s incentive-based regulation (IBR) framework, allowing power producers to adapt tariffs to variable fuel prices, thus enhancing economic resilience in electricity generation. Emphasising the influence of commodity prices, such as coal, gas, and LNG, on generation costs, this study highlights the need for proactive forecasting to aid large consumers, eliminating dependency on semi-annual ICPT price releases. By employing the ARIMA, moving average (MA), and LSSVM methods, the study found that the ARIMA model outperforms the others in fuel price forecasting, with minimal differences from the LSSVM for ICPT prices. Notably, the ARIMA and LSSVM models closely align with actual ICPT tariffs for specific periods, predicting a decrease in ICPT prices for January–June 2024, offering valuable insights for budgeting and planning. This study suggests an extension for future research, particularly in refining the forecasting methods. These will ultimately benefit consumers through more predictable and stable electricity prices, fostering economic growth, and enhancing energy security in the region. Future research can also explore the latest powerful forecasting method that is appropriate for application. Meanwhile, the improvement in the ARIMA’s performance also needs to be considered throughout enhancing some multivariate measures for the p-dimension distribution, such as skewness and kurtosis characteristics [31,32], and other appropriate extension methods.
Author Contributions
F.K.K.: methodology, writing–original draft preparation, software. M.F.S.: supervision, writing, visualization. F.A.Z.: software, methodology, validation. M.S.A.H.: writing review and editing. N.H.S.: results validation, investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to restrictions privacy.
Acknowledgments
The authors would like to thank Universiti Teknikal Malaysia Melaka (UTeM) and International Islamic University Malaysia for all the support given.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Chen, Y.; Li, M.; Yang, Y.; Li, C.; Li, Y.; Li, L. A hybrid model for electricity price forecasting based on least square support vector machines with combined kernel. J. Renew. Sustain. Energy 2018, 10, 055502. [Google Scholar] [CrossRef]
- Sibeperegasam, M.; Ramachandaramurthy, V.K.; Li, F.; Walker, S. De-Regulation of Electricity Industry: A Malaysian Perspective. Int. J. Electron. Electr. Eng. 2020, 8, 17–23. [Google Scholar] [CrossRef]
- Sulaima, M.F.; Hanipah, S.A.A.; Razif, N.R.A.; Razak, I.A.W.A.; Kadir, A.F.A.; Bohari, Z.H. Industrial Energy Load Profile Forecasting under Enhanced Time of Use Tariff (ETOU) using Artificial Neural Network. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 204–209. [Google Scholar] [CrossRef]
- Abidin, N.Z.Z.; Ibrahim, J.B. Embracing renewables—Overcoming integration challenges from Malaysia’s utility perspective. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar] [CrossRef]
- Sibeperegasam, M.; Ramachandaramurthy, V.K.; Walker, S.; Kanesan, J. Malaysia’s electricity market structure in transition. Util. Policy 2021, 72, 101266. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Imani, M.; Ghassemian, H. Electrical Load Forecasting Using Customers Clustering and Smart Meters in Internet of Things. In Proceedings of the 9th International Symposium on Telecommunication: With Emphasis on Information and Communication Technology, IST 2018, Tehran, Iran, 17–19 December 2018; pp. 113–117. [Google Scholar] [CrossRef]
- Aguilar, J.; Garces-jimenez, A.; R-moreno, M.D.; García, R. A systematic literature review on the use of artificial intelligence in energy self-management in smart buildings. Renew. Sustain. Energy Rev. 2021, 151, 111530. [Google Scholar] [CrossRef]
- Porteiro, R.; Nesmachnow, S. Forecasting hourly electricity demand of Uruguay for the next day using artificial neural networks. In Proceedings of the 2020 IEEE PES Transmission and Distribution Conference and Exhibition—Latin America, T and D LA 2020, Montevideo, Uruguay, 28 September–2 October 2020; pp. 8–13. [Google Scholar] [CrossRef]
- Tenaga Nasional Berhad (TNB). Integrated Annual Report 2020; TNB: Kuala Lumpur, Malaysia, 2020; 360p. [Google Scholar]
- Singh, N.; Mohanty, S.R. A Review of Price Forecasting Problem and Techniques in Deregulated Electricity Markets. J. Power Energy Eng. 2015, 3, 1–19. [Google Scholar] [CrossRef]
- Hendikawati, P.; Subanar; Abdurakhman; Tarno. A survey of time series forecasting from stochastic method to soft computing. J. Phys. Conf. Ser. 2020, 1613, 012019. [Google Scholar] [CrossRef]
- Cruz, A.; Muñoz, A.; Zamora, J.L.; Espínola, R. The effect of wind generation and weekday on Spanish electricity spot price forecasting. Electr. Power Syst. Res. 2011, 81, 1924–1935. [Google Scholar] [CrossRef]
- Gao, G.; Lo, K.; Fan, F. Comparison of ARIMA and ANN Models Used in Electricity Price Forecasting for Power Market. Energy Power Eng. 2017, 9, 120–126. [Google Scholar] [CrossRef]
- Almeshaiei, E.; Soltan, H. A methodology for Electric Power Load Forecasting. Alex. Eng. J. 2011, 50, 137–144. [Google Scholar] [CrossRef]
- Abedinia, O.; Amjady, N.; Zareipour, H. A New Feature Selection Technique for Load and Price Forecast of Electrical Power Systems. IEEE Trans. Power Syst. 2017, 32, 62–74. [Google Scholar] [CrossRef]
- Liu, H.; Shen, X.; Tang, X.; Liu, J. Day-Ahead Electricity Price Probabilistic Forecasting Based on SHAP Feature Selection and LSTNet Quantile Regression. Energies 2023, 16, 5152. [Google Scholar] [CrossRef]
- Azadeh, A.; Moghaddam, M.; Khakzad, M.; Ebrahimipour, V. A flexible neural network-fuzzy mathematical programming algorithm for improvement of oil price estimation and forecasting. Comput. Ind. Eng. 2012, 62, 421–430. [Google Scholar] [CrossRef]
- Mei, J.; He, D.; Harley, R.; Habetler, T.; Qu, G. A random forest method for real-time price forecasting in New York electricity market. In Proceedings of the IEEE Power and Energy Society General Meeting, National Harbor, MD, USA, 27–31 July 2014. [Google Scholar] [CrossRef]
- Mustaffa, Z.; Sulaiman, M.H.; Kahar, M.N.M. Training LSSVM with GWO for price forecasting. In Proceedings of the 2015 4th International Conference on Informatics, Electronics and Vision, ICIEV, Fukuoka, Japan, 15–18 June 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, Z.; Yang, S. Day-ahead electricity price forecasting by a new hybrid method. Comput. Ind. Eng. 2012, 63, 695–701. [Google Scholar] [CrossRef]
- Xie, L.; Zheng, H.; Zhang, L. Electricity Price Forecasting by Clustering-LSSVM. In Proceedings of the 2007 International Power Engineering Conference (IPEC 2007), Singapore, 3–6 December 2007; pp. 697–702. [Google Scholar]
- Ge, Q.; Guo, C.; Jiang, H.; Lu, Z.; Yao, G.; Zhang, J.; Hua, Q. Industrial Power Load Forecasting Method Based on Reinforcement Learning and PSO-LSSVM. IEEE Trans. Cybern. 2022, 52, 1112–1124. [Google Scholar] [CrossRef] [PubMed]
- Emhamed, A.A.; Shrivastava, J. Electrical load distribution forecasting utilizing support vector model (SVM). Mater. Today Proc. 2021, 47, 41–46. [Google Scholar] [CrossRef]
- Ali, A.N.F.; Sulaima, M.F.; Razak, I.A.W.A.; Kadir, A.F.A.; Mokhlis, H. Artificial Intelligence Application in Demand Response: Advantages, Issues, Status, and Challenges. IEEE Access 2023, 11, 16907–16922. [Google Scholar] [CrossRef]
- Mustaffa, Z.; Yusof, Y.; Kamaruddin, S.S. Gasoline Price Forecasting: An Application of LSSVM with Improved ABC. Procedia—Soc. Behav. Sci. 2014, 129, 601–609. [Google Scholar] [CrossRef]
- Lee, M.H.L.; Ser, Y.C.; Selvachandran, G.; Thong, P.H.; Cuong, L.; Son, L.H.; Tuan, N.T.; Gerogiannis, V.C. A Comparative Study of Forecasting Electricity Consumption Using Machine Learning Models. Mathematics 2022, 10, 1329. [Google Scholar] [CrossRef]
- Bandyopadhyay, G. Gold Price Forecasting Using ARIMA Model. J. Adv. Manag. Sci. 2016, 4, 117–121. [Google Scholar] [CrossRef]
- Singh, S.; Parmar, K.S.; Makkhan, S.J.S.; Kaur, J.; Peshoria, S.; Kumar, J. Study of ARIMA and least square support vector machine (LS-SVM) models for the prediction of SARS-CoV-2 confirmed cases in the most affected countries. Chaos Solitons Fractals 2020, 139, 110086. [Google Scholar] [CrossRef] [PubMed]
- Department of Energy Management and Industrial Development Suruhanjaya Tenaga (Energy Commission). Malaysia Energy Statistics Handbook; Suruhanjaya Tenaga (Energy Commission): Putrajaya, Malaysia, 2020; Volume 1, p. 86.
- Kollo, T. Multivariate skewness and kurtosis measures with an application in ICA. J. Multivar. Anal. 2008, 99, 2328–2338. [Google Scholar] [CrossRef]
- Loperfido, N. A new kurtosis matrix, with statistical applications. Linear Algebra Its Appl. 2017, 512, 1–17. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).