Abstract
This paper introduces a novel power supply voltage adjustment strategy that can determine the optimum voltage value based on the amount of absorbed power. The novel automatic voltage adjustment technique was called inverse maximum power point tracking (iMPPT). The proposed control strategy consists of a modified maximum power point tracking (MPPT) algorithm (more precisely the P&O method). In this case, the modified MPPT technique establishes the minimum value of the input absorbed power of a consumer load served by a switched-mode power supply (SMPS). The iMPPT adjusts the input power by modifying the input voltage of the main power supply. The served loads are connected to the variable power supply via an interfacing power electronics converter that performs the automatic voltage regulation function (AVR). The optimal value of the input voltage level can be achieved when the input power of the automatic voltage regulation converter is at a minimum. In that case, the energy conversion efficiency ratio is at a maximum, and the overall losses related to the front-end power stage are at a minimum. The proposed technique can also be considered a Maximum Efficiency Tracking (MET) method. By performing the inverse operation of a maximum power point tracking algorithm on the input demanded power of a switched mode power supply (SMPS), the optimum input voltage level can be determined when the maximum energy conversion ratio (related to a given load level) is achieved. The novel proposed iMPPT method can improve the energy conversion ratio from 85% up to approximately 10% in the case of an output power level of 800 W served by a synchronous buck converter at the input voltage level of 350 V. The total amount of recovered power in this situation can be approximately 100 W.
1. Introduction
In the context of modern society, when green and renewable energy is preferred in residential applications, the discussion of powering electrical appliances and devices with direct current (DC) is more and more prevalent in technical literature [1,2,3,4]. Energy storage and conversion efficiency aspects are the main arguments that make direct current nano-grids feasible in residential applications [3]. The nano-grid can be considered the total amount of electrical wiring and equipment in a home or residential place. The micro-grid can connect multiple residential sites or homes in a hood.
The served loads (energy consumers) within the residential nano-grid are connected to the main high-voltage nano-grid bus via a DC-DC power electronic converter that acts as a switched-mode power supply. Automatic voltage level regulation is the main function of the interfacing DC-DC power electronic converter [3].
This paper proposes a new power supply method for residential nano-grids in which the main bus voltage level can be variable if the final loads are connected to the bus via a switched mode power supply (or power electronics converter) that performs the automatic voltage level regulation electronic function [5]. There are also different types of converters that serve as renewable energy production and storage means, but they also perform the automatic voltage level regulation function. The public AC grid can also be connected to the variable voltage DC bus of the nano-grid via a fully bi-directional PWM controlled inverter—rectifier converter (transistor-based controlled rectifier) [6]. A variable voltage adjustment decision unit is also part of the nano-grid. This unit can be a real-time embedded computing system that measures the power on the main bus and determines the optimum voltage level related to the demanded power level and the available power from the renewables and the public AC grid [7,8,9]. The specialized embedded computing device has digital I/Os and analog I/Os that can control the master power electronics converter that drives the main grid bus. The whole architecture of the variable voltage nano-grid can be observed in the following figure (Figure 1) [7,8].
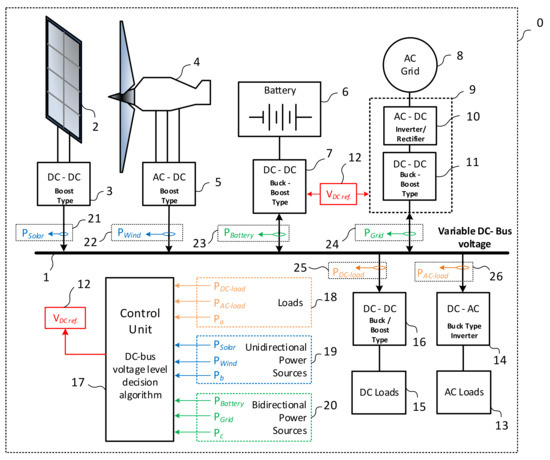
Figure 1.
The architecture of a variable voltage level DC nano-grid [7,8,9].
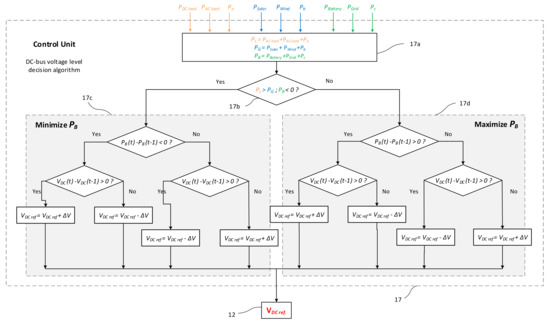
Figure 2.
The variable supply voltage adjustment strategy based on the inverse maximum power point tracking technique (iMPPT) [7,8,9,10].
- 0
- Variable voltage nano-grid architecture
- 1
- Variable DC bus voltage
- 2
- Photovoltaic panels (PV) array
- 3
- Boost converter for the PV array
- 4
- Micro wind turbine
- 5
- Micro wind turbine boost converter
- 6
- Battery bank
- 7
- Battery bank bi-directional converter
- 8
- AC public grid
- 9
- AC public grid bi-directional power stage
- 10
- AC-DC PWM controlled inverter/rectifier
- 11
- DC-DC bi-directional converter
- 12
- DC-Bus voltage reference
- 13
- AC loads
- 14
- AC loads buck/step-down converters
- 15
- DC loads
- 16
- DC loads buck/step-down converters
- 17
- Logic control unit/specialized embedded computing system
- 17a
- Power measurement module
- 17b
- Power value logic decisional module
- 17c
- Inverse maximum power point tracking (iMPPT) algorithm that minimizes “PB”
- 17d
- Inverse maximum power point tracking (iMPPT) algorithm that maximizes “PB”
- 18
- Centralized loads measurement module
- 19
- Centralized unidirectional power sources measurement module
- 20
- Centralized bidirectional power sources measurement module
- 21
- PV array power measurement module
- 22
- Wind turbine power measurement module
- 23
- Battery bank power measurements module
- 24
- AC public grid power measurement module
- 25
- DC loads power measurement module
- 26
- AC loads power measurement module
The proposed architecture of the variable voltage nano-grid [7,11] and the voltage adjustment strategy are parts of the pending patent called “Micro-grid of variable DC voltage and its control method” [7,8]. This is a Romanian patent pending application at OSIM (the National State Office of Trademarks and Inventions) applied on 19 December 2019 called “Micro-grid of variable DC voltage and its control method”. The patent application was also published in the “Official Bulletin of Industrial Property” in the section “Patents” [8,11].
The inverse maximum power point tracking (iMPPT) strategy [8,10] is a modified “Perturb and Observe” (P&O) algorithm that minimizes the input power of the interfacing power electronics converter by adjusting the main power supply or bus voltage level. An optimum bus voltage level will be determined by the iMPPT algorithm and is related to the amount of power demanded by the final served loads. The same algorithm can also act as a classic perturb and observe MPPT method when the nano-grid works in bi-directional mode, and the excessive power is injected into the public AC grid or battery [7,8,11].
The main advantage of using iMPPT consists of the fact that the overall losses related to the energy conversion process can be minimized by selecting the optimum voltage level related to the power level demanded by the attached loads [12,13].
2. Methodology and Experimental Setup for Proving the Main Concept
The main concept of this paper consists of the fact that the input power, absorbed by an electric load supplied via a switched-mode power supply, can be reduced if an optimum value of the input voltage is set. The maximum conversion efficiency possible, related to the output power, can be reached at the optimum input voltage level. Finally, an automatic voltage adjustment strategy can be implemented to improve the conversion efficiency of the considered power stage. The iMPPT method in this case can be considered a maximum efficiency tracking (MET) method [9,10,11]. The only requirement for the variable DC bus interfacing converter is that it can operate in a wide range of input voltage levels. A synchronous buck converter will be used (Figure 3) [14,15,16,17].
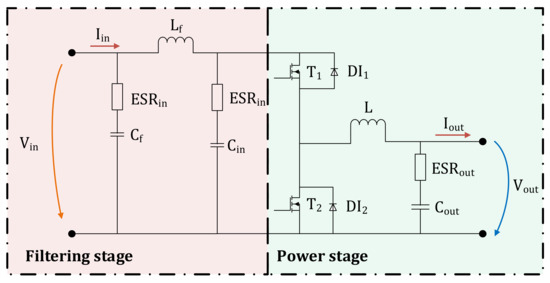
Figure 3.
The synchronous buck converter topology.
The synchronous (step-down) buck interfacing converter will act as a switched-mode power supply between the variable voltage DC bus and the final served load. The output voltage “Vout” of the converter will be kept constant by a “closed-loop” control strategy based on a proportional—integral (PI) regulator [18,19]. The PI controller performs the automatic voltage level regulation function on the output voltage level “Vout” [20,21,22]. The output voltage will remain constant regardless of the variation in the output load resistance “RL” or input voltage “Vin” [18,19,20,21,22].
The PI controller will automatically adjust the duty cycle “d” so that the output voltage level measured by the feedback sensor “Vm” will match the reference voltage “Vref” (Figure 4) [18,19,23,24].
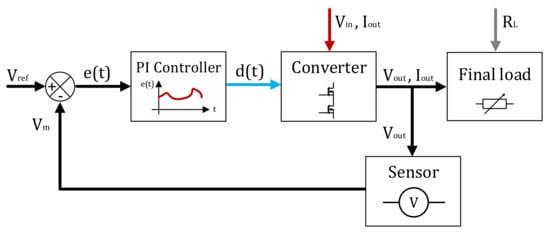
Figure 4.
Automatic voltage regulation based on proportional—integral controller [8,18,19,24].
According to the “open-loop” working mode equation of the considered power electronics converter (Equation (1)), the input voltage “Vin” and the output current “Iout” will act as perturbation parameters in the “closed-loop” system [8,18,19,24].
By modifying the input voltage “Vin” or the final load resistance “RL”, which directly affects the output current “Iout”, the PI controller will need to determine dynamically a new value for the duty cycle “d”, directly adjusting the output voltage “Vout” so that it will match the reference voltage “Vref” even for new conditions imposed by perturbations (Equation (2)). The overall system error will be convergent to zero to match the closed-loop system stability conditions (Figure 5) [8,18,19,24].
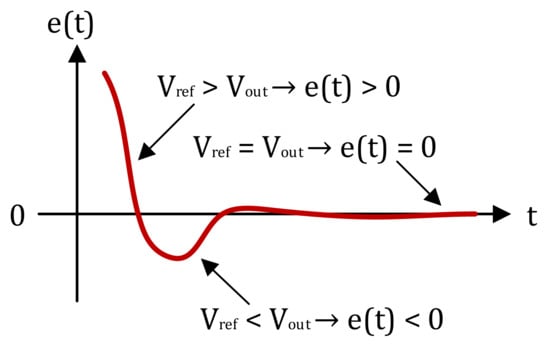
Figure 5.
The overall system error “e(t)” over time in a closed loop system [18,19].
Considering the duty cycle “d” as being time dependent “d(t)”, the overall system error “e(t)” can be determined from the following equation [8,18,19,24]:
The system stability condition will be
The PI controller adjusts the duty cycle by the following equation [8,18,19,24]:
Considering the buck converter as the “plant” in the system, the expression becomes
For the steady-state condition, when “e(t) = 0”, the expression becomes [8,18,19,24]
As a short conclusion over the presented control theory, the PI controller automatically adjusts the duty cycle “d(t)” over time in such a way that the overall system error converges to zero. It means that the output voltage “Vout” matches the initial value of the reference voltage “Vref”. The average effect that can be observed at the input of the converter is that it dynamically adjusts its “internal impedance” in such a way that the output voltage “Vout” remains constant regardless of the external system perturbations [18].
If the output load impedance remains constant and the output voltage remains constant, the system works in “constant power” (CP) mode [25,26]. The working principle of a power electronics converter in CP mode can be equivalent to a simple circuit in which the series resistance “r” controls the amount of current absorbed by the load and the final load resistance “RL” controls the voltage drop at the output of the circuit. Both resistances are variable, and those are adjusted in such a way that the power consumption from the main power supply “E” remains constant even if the main power supply voltage changes (Figure 6). An ideal average model of the converter can be equivalent to the series resistance “r” which represents the converter working in automatic voltage regulation mode, and the final load “RL” represents the real served load which absorbs the load current “IL” [25,26].
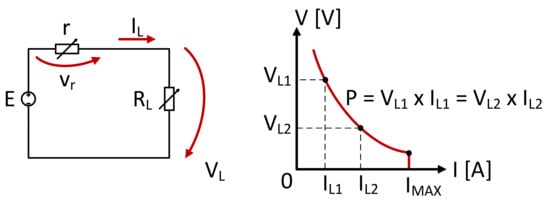
Figure 6.
The constant power (CP) working mode of a simple circuit [8].
Assuming the fact that the power supply voltage level (E1 and E2) and the final load resistance (RL1 and RL2) can be modified, while the series resistance “r” remains constant, the following equations will describe the constant power (CP) mode [8,25,26]:
If the amount of absorbed power changes over time, the finite difference between the final and initial value of the load power “ΔPL” shall be different than zero. If the power remains constant, the finite difference is zero. Based on this assumption, the equations (Equations (8)–(10)) were expressed. This means that the electrical power can be expressed in multiple ways, considering or not the series “r” resistance. Another important fact to mention is that electrical power can be expressed as a product of two variables: voltage and current. By representing the electrical power in an “I-V” axis system, a rectangular surface can be obtained. The side dimensions of the rectangular surface are determined by the voltage and current values. The area of the rectangular surface represents electrical power. The same surface area can be represented in two ways, for example, the long side that represents the voltage shall be greater than the side that represents the current and vice versa. Practically, electrical power can be represented as a high value of current and a low value of voltage or a high value of voltage and a low value of current; thus, in both cases, the same amount of electrical power can be obtained, and the same surface area can be plotted in the “I-V” plane in both cases (Figure 7) [17,20].
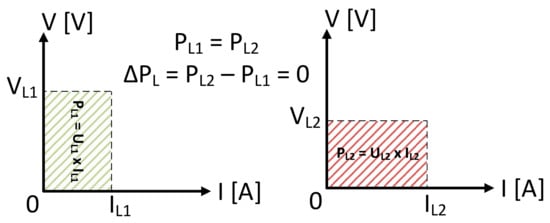
Figure 7.
I-V surface plot of a constant power (CP) situation [8,25,26].
The input voltage level in this working mode (CP) can be modified without affecting the output power supplied by the converter to the final load (Figure 8).
Figure 8.
Nano-grid bus voltage or input voltage of the power electronics converter [8,25,26].
The difference “ΔPC” between the input power “Pin” and the output power “Pout” represents the total amount of power losses related to the conversion process (Equation (11)).
The overall losses include reactive losses, switching and conduction losses and parasitic losses (ex. parasitic resistance, inductance, and capacity) (Figure 9) [8,27,28,29].
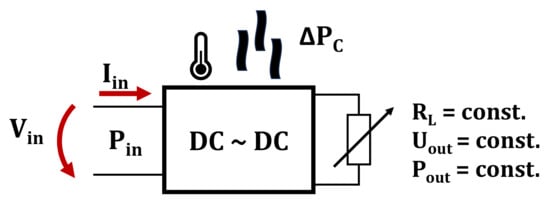
Figure 9.
Power electronics converter losses in output constant power (CP) mode [8,27,28,29].
The ratio of the output power “Pout” and the input power “Pin” represents the conversion efficiency, and it can be described as a non-dimensional percentage (Equation (12)). The efficiency ratio represents a two-variable function, which can be plotted as a surface in a tridimensional axis system or a two-dimensional family of characteristic curves [8,27,28,29].
By changing the input voltage in a constant power (CP) working mode of a switched mode power supply, the total amount of power loss can be reduced significantly. The input power will decrease as the total power loss related to the conversion process decreases. A minimum point on the “losses vs input voltage” plot will be represented. That point corresponds to the maximum efficiency and minimum input power. The input voltage related to the minimum input power represents the optimum voltage corresponding to the actual output load power (Equation (13)) (Figure 10 and Figure 11) [8,27,28,29].
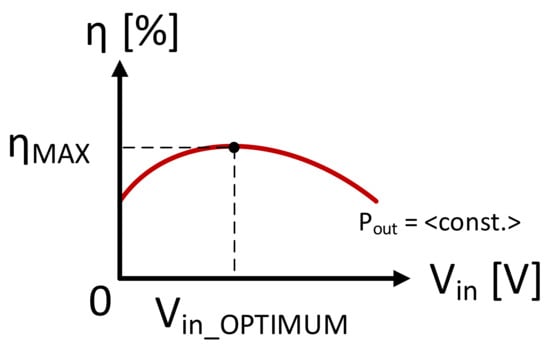
Figure 10.
Efficiency vs. input voltage plot of a power electronics converter in output CP mode [8].
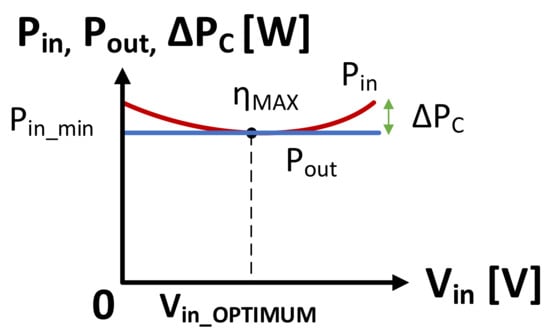
Figure 11.
Optimum input voltage level of a power electronics converter operating in CP mode [8].
To prove the main concept described within this paper, an experimental setup has been implemented using specialized laboratory equipment (Figure 12) such as:

Figure 12.
Laboratory experimental setup and workbench [8].
- -
- programmable DC voltage power supply Itech IT6534C (light blue mark)
- -
- AXIO MET AX-582B multimeter for measuring input current (blue mark)
- -
- AXIO MET AX-582B multimeter for measuring input voltage (pink mark)
- -
- power resistor with a value of 1 Ω for simulating the cable length (gray mark)
- -
- National Instruments MyRIO 1900—embedded development kit (orange mark)
- -
- synchronous buck step-down converter (dark yellow mark)
- -
- AXIO MET AX-582B multimeter for measuring output current (dark blue mark)
- -
- AXIO MET AX-582B multimeter for measuring output voltage (dark brown mark)
- -
- adjustable sources for powering annex modules (light green mark)
- -
- IT8616 programmable electronic load (light yellow mark)
The experimental setup block diagram is shown in Figure 13.
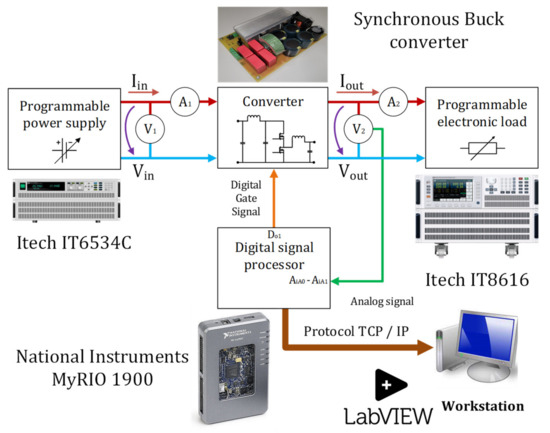
Figure 13.
Block diagram of the experimental setup [8].
According to the experimental setup block diagram, the input of the synchronous buck converter was connected to a high-voltage DC programmable power supply (Itech IT6534C). Two AXIO MET AX-582B multimeters were used on the input side of the converter to measure the input voltage and the input current. On the input side, a one-ohm high-power resistor was also connected in series with the converter to simulate the cable’s length loss in a residential nano-grid. On the output side of the converter, a high-power programmable electronic load was connected. Also, on the output side of the converter, two AXIO MET AX-582B multimeters are used to measure the output current and voltage of the power electronics converter. The PWM digital gate signal, for the converter’s main switching transistors was provided by the National Instruments MyRIO 1900 development kit. MyRIO acts as a digital signal processor (DSP) because it also measures the output voltage of the converter via a voltage measuring module based on Avago ACPL 7900 isolated amplifier (Figure 14), and it runs the automatic voltage regulation control strategy, developed in National Instruments LabVIEW [8].

Figure 14.
Avago ACPL 7900 isolated amplifier-based voltage measuring module [8].
Based on the voltage feedback, MyRIO generated the desired duty cycle for the PWM gate signal of the synchronous buck converter [30] (Figure 15). A proportional—integral controller-based strategy was implemented in My Rio’s memory, using the NI LabVIEW graphical programming environment (Figure 16) [8].

Figure 15.
DC-DC Synchronous step-down buck converter prototype [8].
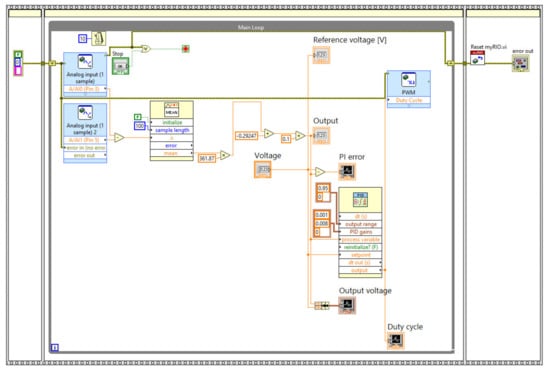
Figure 16.
Automatic voltage regulation control law implemented in NI LabVIEW for MyRIO [8].
After implementation of the experimental setup, the following test steps will be performed to collect numerical data-points for further study on the variable voltage supplying diverse DC consumer loads [8]:
- -
- At the input of the converter, the initial input voltage value will be set at 100 V and data-points will be collected in a summary table; after this step the input voltage value will be increased by another 25 V and data-points will be collected again in the summary table until the final value of 350 V is reached.
- -
- The output voltage will be kept constant at 72 V using the NI MyRIO embedded controller, with the control law implemented. The control loop runs at a 10 ms time step within LabVIEW and MyRIO.
- -
- The PID controller coefficients were set empirically based on the concept of minimizing the closed loop system’s error in the shortest possible time interval (a Ziegler-Nichols PID tuning method approach based on Equations (3), (4) and (6)). The determined controller coefficients are kP = 0.001 and kI = 0.008, kD = 0 and the saturation or limit range for the PWM signal and the duty cycle is [0, 0.95]. The controller is a classical PID model implemented in LabVIEW based on the classical mathematical approach of a simple (non-parallel) PID controller [18,19].
- -
- Using the programmable electronic load, constant power values will be set at the output of the power electronics converter.
- -
- At each new value of the output power, a complete input voltage sweep cycle will be performed, and the data-point will be recorded in a summary table.
- -
- Using the input and output values of voltage and current, the input and output power, the conversion efficiency, the overall converter losses and the input impedance values will be determined.
- -
- Based on all data-points and the determined parameters, functional characteristic curves of the power electronics converter will be plotted and analyzed in different situations.
After examining the real data-points collected from the physical experimental setup, a Hardware-In-the-Loop (HIL) (Figure 17) simulation of the automated variable supply voltage adjustment strategy setup will be implemented using the following equipment:
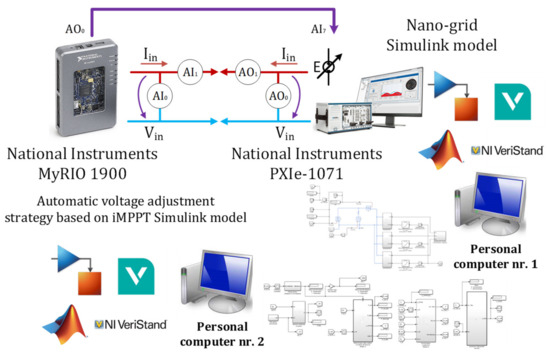
Figure 17.
Principial block diagram of the HIL system setup [8].
- -
- Two PCs running NI 2021 SP1 Software Bundle including VeriStand (same version).
- -
- MyRIO-1900 embedded controller.
- -
- NI PXIe-1071 Hardware In the Loop Real-Time simulation computer.
- -
- MathWorks Matlab-Simulink R2018b + NI VeriStand model framework.
The NI MyRIO-1900 embedded controller will run the iMPPT variable voltage adjustment strategy. The control law will be implemented within NI MyRIO using the Matlab-Simulink and NI VeriStand model framework (Figure 18). NI VeriStand will be installed on both computers, one for MyRIO and one for PXI [8].
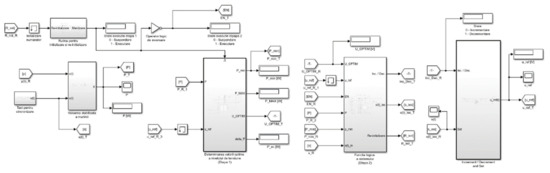
Figure 18.
The iMPPT automatic voltage adjustment strategy [8].
The PXI will run a nano-grid model with three DC loads supplied via a synchronous step-down buck converter. In this simulation (HIL simulation) the “converter + load” group will be emulated as a variable resistor that changes its impedance according to the input voltage level based on a look-up table. The values within the look-up table were determined based on the real input current and voltage values (Figure 19 and Figure 20) [8].
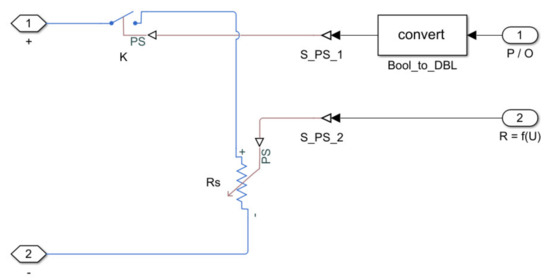
Figure 19.
The variable load equivalent model of the “converter + load” group [8].
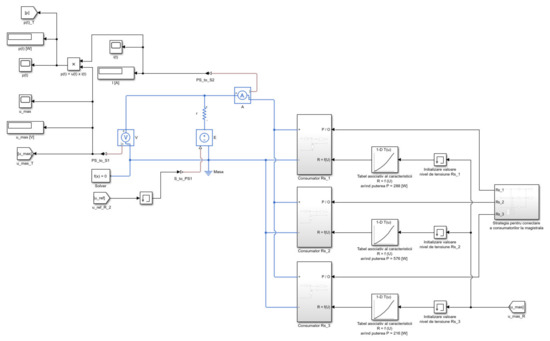
Figure 20.
The nano-grid Simulink model [8].
The HIL simulation models were initially tested in offline simulations within the Simulink. The nano-grid model was implemented using Simulink SimScape. Three different power values were set for the DC consumer loads [8].
The final VeriStand results shall match the offline simulation model results.
The iMPPT-based automatic voltage adjustment technique sweeps the input voltage from the initial value of 100 V and stores the input voltage and input power values in one bi-dimensional array. A minimum input power value will be identified and its corresponding optimum input voltage value. The corresponding optimum input voltage value will be set by the special technique “incremental and settle” [31] to allow steady-state operation and data acquisition in the computing system. The workflow of the iMPPT-based automatic voltage adjustment technique can be observed in (Figure 21), [8].
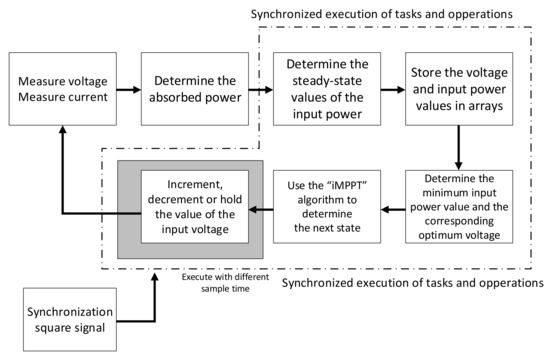
Figure 21.
The iMPPT-based automatic voltage adjustment technique workflow [8].
In the next step the main results will be presented.
3. Results
To analyze the behavior of the electronic converter powered with variable voltage [31], the first step is to plot the functional characteristic curves of the studied converter.
Three nominal output power ratings were selected from the three voltage ranges (low, medium and high): Pout_1 = 216 W, Pout_2 = 288 W and Pout_3 = 576 W. For these three cases, the main experimental results will be presented.
In the first case (Table 1), it was found that the maximum conversion efficiency ratio ηMAX = 96.883% was obtained at the level of input voltage of Vin = 175 V, (Figure 22). At the same voltage level, both the minimum input power Pin_min = 222.95 W and the minimum overall loss at the converter level ΔPc_min = 6.95 W were recorded (Figure 23 and Figure 24). For the input voltage level of Vin = 100 V, the minimum value of the efficiency was recorded ηmin = 95.872% [31].

Table 1.
Experimental results for case 1—Output power Pout = 216 W—constant.
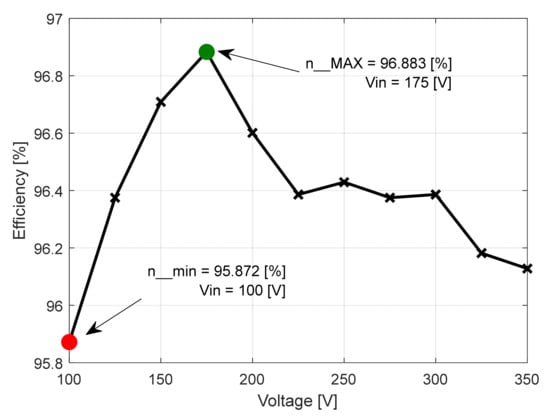
Figure 22.
Conversion efficiency related to the input voltage functional characteristic curve [8].
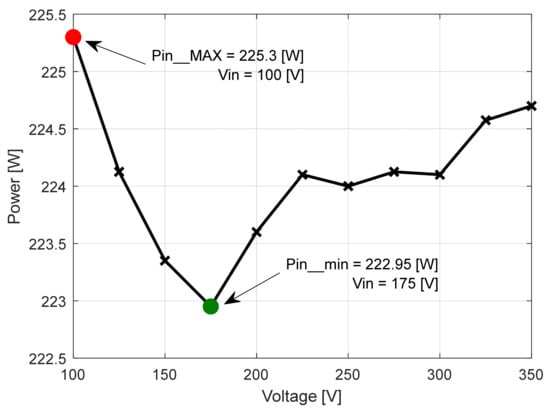
Figure 23.
Input power related to the input voltage functional characteristic curve [8].
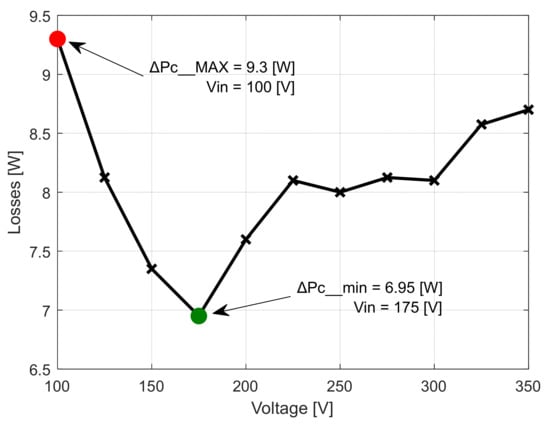
Figure 24.
Overall losses related to the input voltage functional characteristic curve [8].
For the same voltage level, both the maximum input power Pin_MAX = 225.3 W and the maximum value of losses recorded, namely ΔPc_MAX = 9.3 W, were obtained. Both the recovered value of conversion efficiency and overall converter loss levels can be determined using the following expressions:
In the second case (Table 2), it was found that the maximum efficiency ηMAX = 96.677% was obtained at the input voltage level of Vin = 225 V (Figure 25). At the same voltage level, both the minimum input power Pin_min = 297.9 W and the minimum overall converter loss, named ΔPc_min = 9.9 W, were recorded (Figure 26 and Figure 27). At the input voltage level of Uin = 100 V, the minimum value of the conversion efficiency was recorded, named ηmin = 94.706%. At the same voltage level, both the maximum value of the input power Pin_MAX = 304.1 W and the maximum value of converter loss, namely ΔPc_MAX = 16.1 W, were obtained. Thus, both the recovered amount of conversion efficiency and overall converter losses can be determined based on the following equations:

Table 2.
Experimental results for case 2—Output power Pout = 288 W—constant.
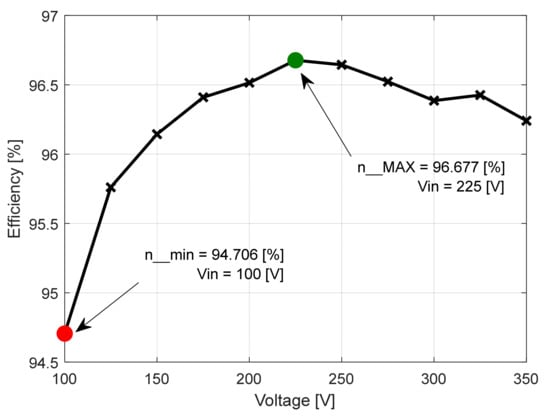
Figure 25.
Conversion efficiency related to the input voltage functional characteristic curve [8].
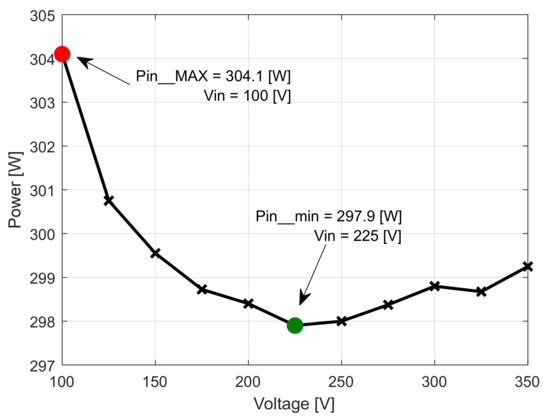
Figure 26.
Input power related to the input voltage functional characteristic curve [8].
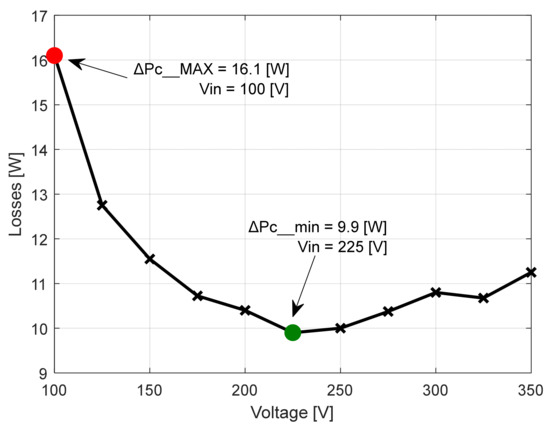
Figure 27.
Overall losses related to the input voltage functional characteristic curve [8].
For the third case (Table 3), the maximum conversion efficiency ηMAX = 95.956% was obtained at the input voltage level of Vin = 325 V, (Figure 28). At the same voltage level, both the minimum input power Pin_min = 600.75 W and the minimum overall converter loss ΔPc_min = 24,275 W were recorded (Figure 29 and Figure 30). At the input voltage level named Uin = 100 [V], the minimum value of the conversion efficiency was recorded, ηmin = 89.468%. At the same voltage level, both the maximum value of the input power Pin_MAX = 643.8 W and the maximum value of the converter loss, namely ΔPc_MAX = 67.8 W, were obtained. Therefore, the recovered value of the conversion efficiency, as well as of the overall converter losses, can be determined using the following equations:

Table 3.
Experimental results for case 3—Output power Pout = 576 W—constant.
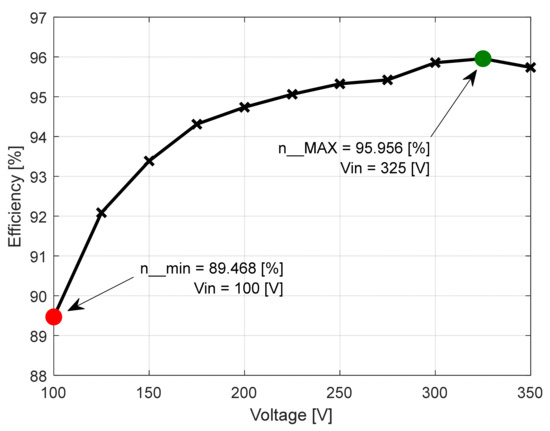
Figure 28.
Conversion efficiency related to the input voltage functional characteristic curve [8].
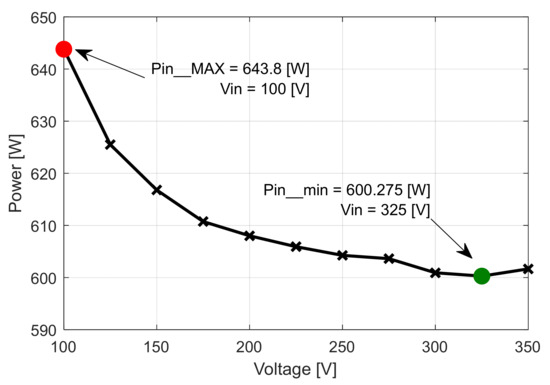
Figure 29.
Input power related to the input voltage functional characteristic curve [8].
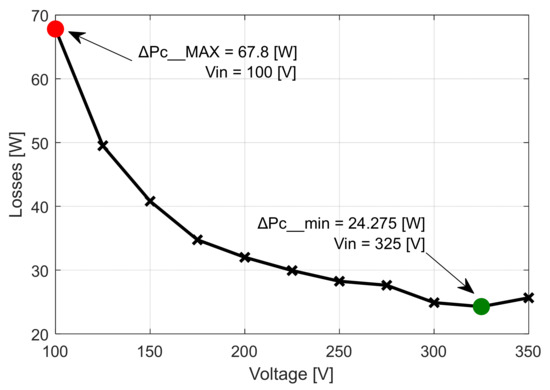
Figure 30.
Overall losses related to the input voltage functional characteristic curve [8].
As a preliminary conclusion over this step, the main concept was proved because, according to the results represented above, the conversion efficiency and overall losses can be reduced by selecting the optimum input voltage level, related to the minimum value of the input power.
Considering this assumption (that the optimum input voltage corresponds to the minimum value of the input power), an automatic voltage adjustment technique was developed first in offline simulations. The MathWorks Matlab-Simulink environment was used to develop the offline simulation model and the Real-Time HIL online simulation hardware-ready model. Two models were built, one for the nano-grid model and one for the automatic voltage adjustment technique.
The virtual DC loads were simulated based on real data recorded in the previous step in the summary tables. More precisely, the impedance of a variable load was adjusted according to a look-up table that contained the real voltage values (Figure 31).
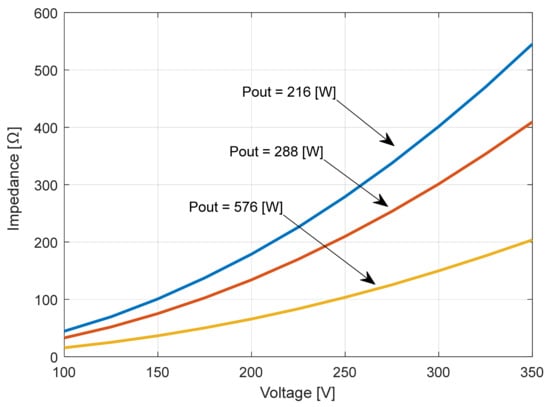
Figure 31.
The input impedance of the “converter + load” group related to input voltage [8,32,33].
By using the “impedance related to voltage” functional characteristic curves of the three cases studied earlier, three variable loads can be simulated by using look-up tables. Those loads emulate the real behavior of the “converter + load” group in the variable input voltage powering conditions and constant power at the output [32,33]. Three variable loads were connected sequentially to the nano-grid within the DC grid Simulink model (Figure 32 and Figure 33).
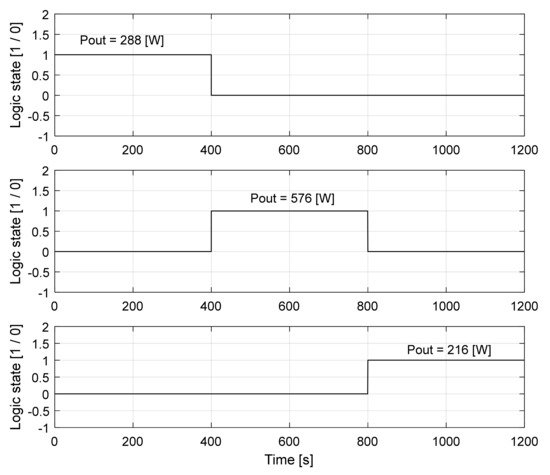
Figure 32.
The connection sequence of the variable loads to the nano-grid [8].
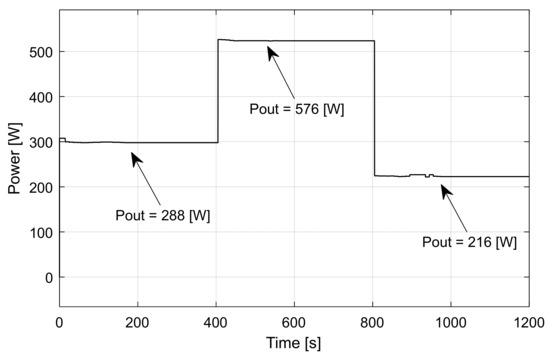
Figure 33.
The absorbed power from the nano-grid [8].
The iMPPT algorithm automatically adjusts the main bus input voltage level so that the absorbed power by the variable loads is always at a minimum for that corresponding demanded load power level (Figure 34).
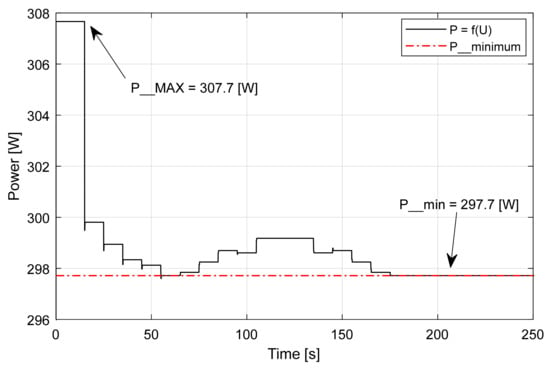
Figure 34.
The iMPPT algorithm always tracks and keeps the input power level at a minimum [8].
The optimum voltage level corresponds to the minimum input power and to the minimum overall loss level. The automatic voltage adjustment technique tracks the minimum input power and sets the voltage level accordingly. The first step to identify the minimum power value is a voltage sweeping operation performed by the iMPPT algorithm. The input power and voltage values are stored in a bi-dimensional array, and then, the minimum value of the input power is determined from the array. In the same row, the optimum input voltage level is stored in the bi-dimensional array (Figure 35). The index of the optimum input voltage value will be determined, and the corresponding value will be extracted from the array (Figure 35) [8].
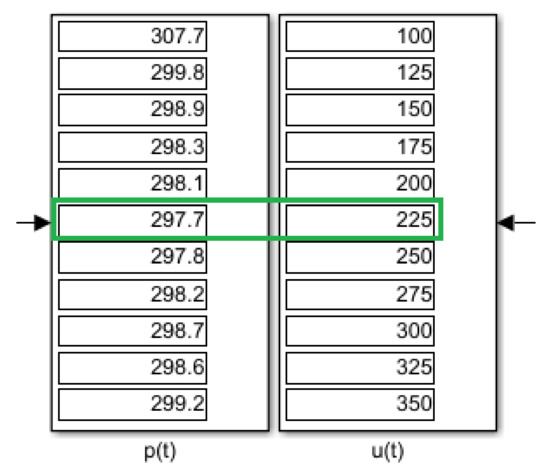
Figure 35.
Determining the minimum input power [8].
The iMPPT algorithm also decides if the voltage level shall be increased or decreased to reach the target level set by the bi-dimensional array fetching operation. If the main absorbed grid power value changes, the iMPPT re-sets the voltage adjustment operation and scans for a new optimum voltage level (Figure 36) [8].
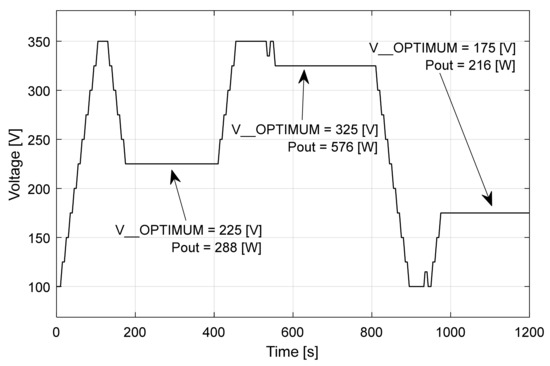
Figure 36.
Determining the new optimum input voltage level in case of power level change [8].
The input absorbed current level from the nano-grid will be also set at an optimum value, not an absolute minimum value (Figure 37).
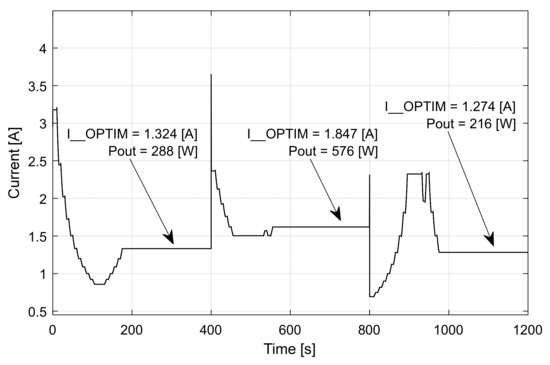
Figure 37.
Determining the new optimum input current level in case of power level change [8].
The math operations are always performed in a steady state. The voltage adjustment technique increases or decreases the voltage discontinuously. The adjustment technique we have novelty called “incremental and settle” (Figure 38 and Figure 39). The data acquisition is also performed in a steady state. A square synchronization signal was used.
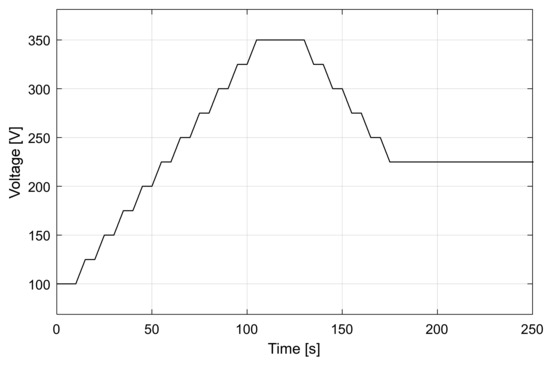
Figure 38.
Discontinuous increment of the input voltage level (incremental and settle) [8].
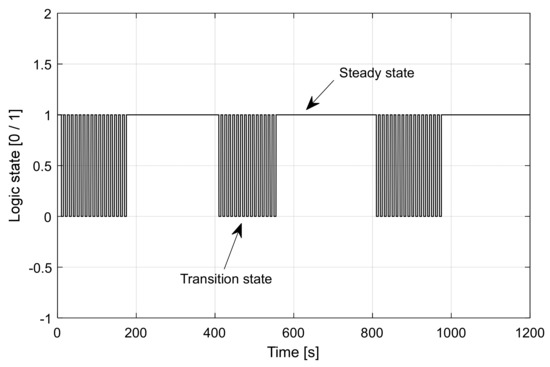
Figure 39.
Square synchronization signal.
In the first experimental step, the voltage level was set manually from the high-power DC power supply front panel knob. In the second experimental step, an offline Simulink simulation model was developed to obtain the automatic voltage adjustment technique. The offline simulation was performed using real tabular data recorded under real lab conditions using a physical prototype [8].
In the third experimental step, a real-time online Hardware-In-the-Loop (HIL) simulation will be performed (Figure 40).

Figure 40.
Hardware In the Loop (HIL) experimental setup [8].
Both Simulink Models (the nano-grid model and the voltage adjustment model) were imported onto two separate computers running the NI VeriStand and NI Software bundle. For the voltage adjustment model, NI MyRIO was used, and the following dashboard was created (Figure 41):
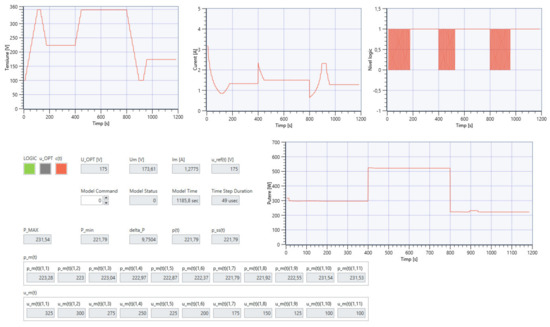
Figure 41.
NI VeriStand dashboard for automatic voltage adjustment model running on MyRIO [8].
For the NI PXIe-1071, the nano-grid Simulink model was also imported in VeriStand, and a dashboard has been created (Figure 42).
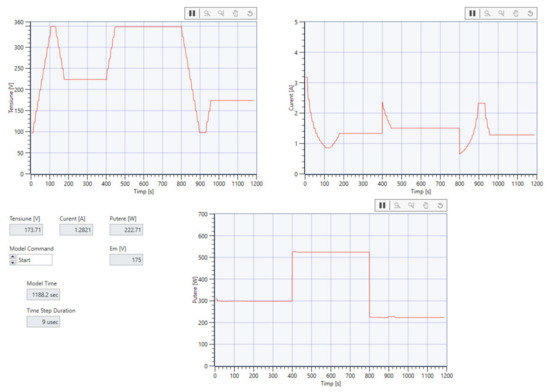
Figure 42.
NI VeriStand dashboard for nano-grid model running on PXIe-1071 [8].
The results of the online HIL simulation correspond to the results obtained in the offline simulation within Matlab-Simulink. It means that the automatic voltage adjustment control strategy runs on the NI MyRIO 1900 embedded controller (Figure 43).
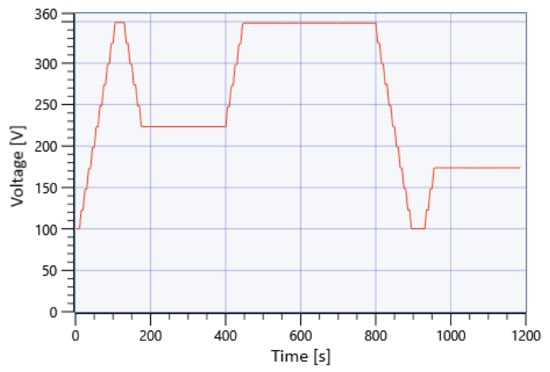
Figure 43.
NI VeriStand voltage adjustment [8].
The automatic voltage adjustment technique determines the new optimum voltage value each time the absorbed power level changes.
The implementation step of the automated voltage adjustment technique on the NI MyRIO 1900 embedded device was tested and confirmed using the Hardware-In-the-Loop (HIL) real-time simulation procedure (Figure 44 and Figure 45).
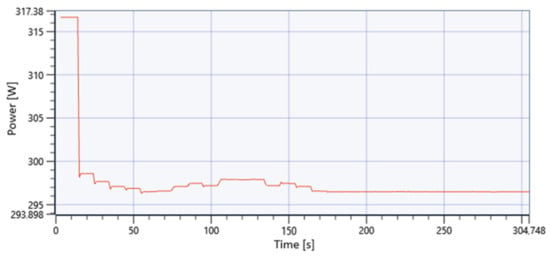
Figure 44.
NI VeriStand minimum input power [8].
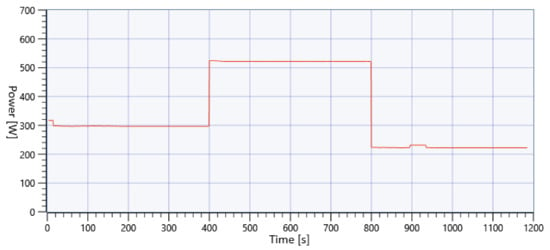
Figure 45.
NI VeriStand overall nano-grid power [8].
4. Discussion
The same test scenarios were performed for 11 different power levels (from 72 W to 792 W). It was found that the variable voltage powering mode applies to a wide range of power levels but predominantly its loss recovery effect can be observed only at higher power levels. The highest amount of power was recovered at the output power level Pout = 792 W, with a total amount of overall loss of ΔPC_REC = 96 W, equivalent to approximately ΔηREC~9.82% percent of nominal efficiency of the converter (Figure 46 and Figure 47).
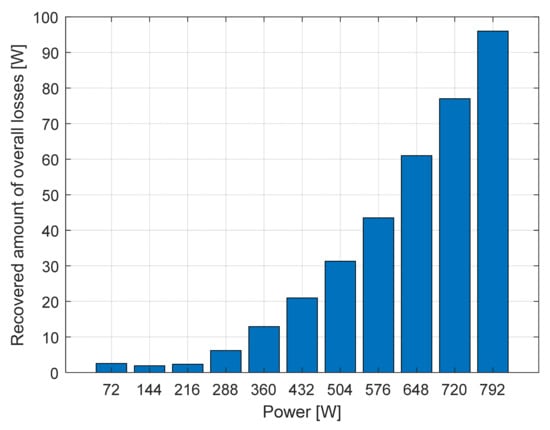
Figure 46.
The amount of recovered overall losses [8].
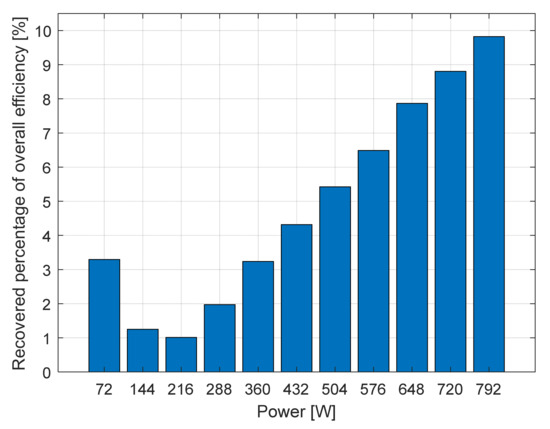
Figure 47.
The amount of recovered conversion efficiency percentage [8].
Also based on empirical data, both the family of characteristics “efficiency depending on input voltage” and “the map of efficiency values related to input voltage and output power” will be plotted (Figure 48 and Figure 49) [8].
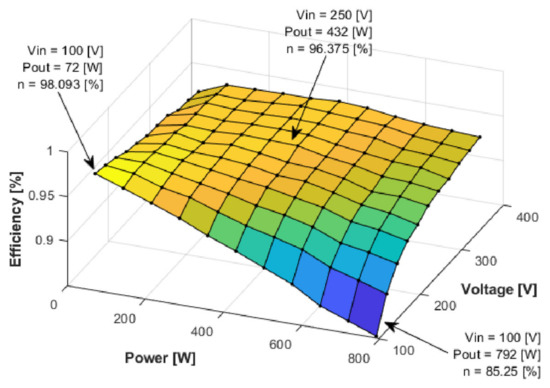
Figure 48.
The energy conversion efficiency map of the power electronics converter [8].
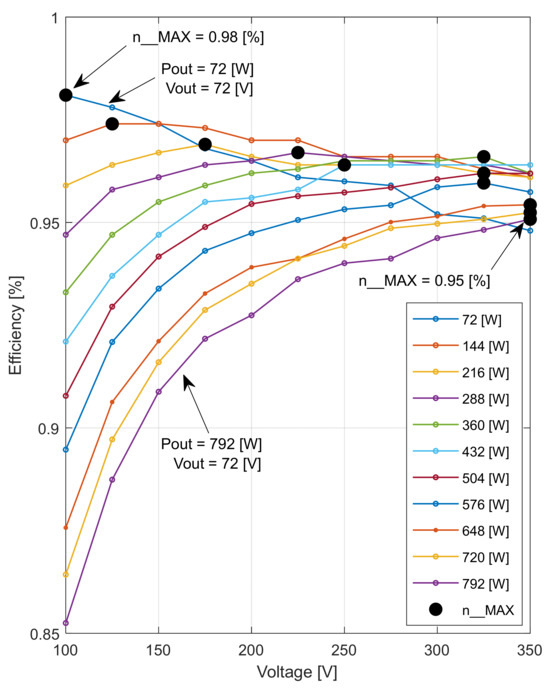
Figure 49.
The functional characteristic curves family of “efficiency vs. input voltage” depicting the distribution of maximum efficiency points related to the input power level [8].
For the implementation step of the automatic input voltage adjust technique of the grid or power supply, the families of characteristic curves alternative to the representation “efficiency related to input voltage” will be used, namely, two more sets of characteristic curves will be plotted, namely “current related to input voltage” and “input impedance related to input voltage” (Figure 50 and Figure 51) [8].
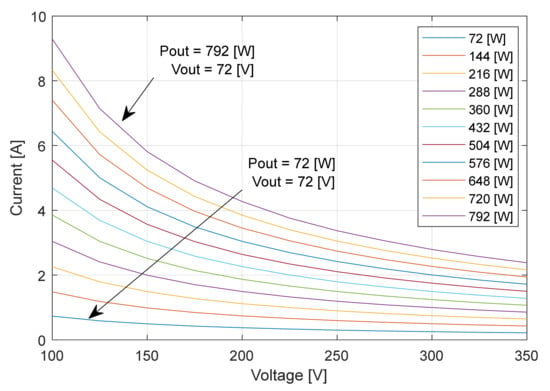
Figure 50.
The functional characteristic curves family of “input current vs. input voltage” [8].
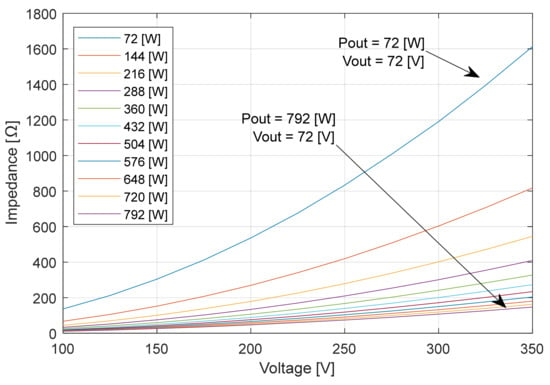
Figure 51.
The functional characteristic curves “input impedance vs. input voltage” [8,32,33].
The recovered values for overall losses and conversion efficiency percentages were determined according to equations (14) and (15), for example. The results were recorded in a summary table (Table 4).

Table 4.
Recovered values of overall power losses and conversion efficiency percentage.
The input current of the power electronics converter is adjusted parabolically, like the constant power (CP) working mode I-V plot when input voltage changes (Figure 6). It means that the synchronous buck converter operates in constant power mode (CP) [8].
The proportional integral controller automatically adjusts the duty cycle in such a way that the output voltage always remains constant. By adjusting the duty cycle in the power electronics converter, its input impedance will be modified (Figure 50). The optimal voltage corresponds to the optimal impedance and the minimum input power [8].
5. Conclusions
Finally, the main conclusions can be summarized as follows:
- -
- Based on representative functional characteristics of consumers (e.g., characteristic curve I = f(V)), it is possible to identify the operating mode [34].
- -
- In the case of a regulated voltage source, the equivalent circuit can be reduced to a constant power consumer load from the point of view of the input side [34].
- -
- The converter adjusts the impedance to serve the final consumer load at the optimal parameters [34].
- -
- The input voltage level can be adjusted in such a way that the conversion efficiency of a regulated switched mode power supply can be improved.
- -
- The novel proposed iMPPT method can improve the energy conversion ratio from 85% up to approximately 10% in case of an output power level of 800 W served by a synchronous buck converter at the input voltage level of 350 V. The total amount of recovered power in this situation can be approximately 100 W.
6. Patents
Based on the principle of optimization of conversion efficiency presented in the previous chapter, a strategy for the automatic voltage regulation for the power supply side level was proposed in a patent application filed with OSIM on 19 December 2019 entitled “Micro-grid of variable DC voltage and its control method” (Figure 1 and Figure 2).
The application was published in the “Official Bulletin of Industrial Property” in the section “Patents” [7,11]. Both the operating logic diagram of the automatic voltage level adjustment strategy and the residential microgrid structure can be observed in the following figures (Figure 1 and Figure 2).
Author Contributions
Conceptualization, L.N.P.; Methodology, C.G.R.; Software, H.C.H.; Validation, P.D.T. and A.M.P.; Writing—original draft, S.I.S.; Writing—review & editing, C.I.M., V.M.S. and N.C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This paper was financially supported by the Project “Network of excellence in applied research and innovation for doctoral and postdoctoral programs/InoHubDoc”, project co-funded by the European Social Fund financing agreement no. POCU/993/6/13/153437.
Data Availability Statement
The data used in this study in order to validate the operation mode in variable input voltage of diverse electronic loads were extracted from bibliographic source [8], the main author’s PhD thesis entitled “Research Aimed at Electricity Management in Electronic Systems with Renewable Sources” published at Technical University of Cluj-Napoca, Romania in 2023. The PhD thesis was based on a Romanian patent pending application at OSIM (the National State Office of Trademarks and Inventions) applied on 19 December 2019 called “Micro-grid of variable DC voltage and its control method”. The patent pending application can be found in the bibliographic [7,11]. Related experimental work over the patent pending application subject was also mentioned in the bibliographic reference [15], “Theoretical efficiency analysis of a buck-boost converter for wide voltage range operation”. Other bibliographic sources were cited in order to validate the experimental results (the conversion efficiency values), such as reference [27] “Efficiency Comparison of Different DC-DC Converter Architectures for a Power Supply of a LiDAR System”. Another important reference to mention for the procedural workflow was the bibliographic source [34], “Behavioral Model of Power Converter - Average models of DC-DC Converters”. Based on the last bibliographic reference, the behavior of the power electronics converter was replicated using variable programmable loads operating in constant power consumption mode. The constant power mode was emulated using look-up tables based on real data recorded from the experimental step.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rodriguez-Otero, M.A.; O’Neill-Carrillo, E. Efficient Home Appliances for a Future DC Residence. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Cordova-Fajardo, M.A.; Tututi, E.S. Incorporating home appliances into a DC home nanogrid. J. Phys. Conf. Ser. 2019, 1221, 012048. [Google Scholar] [CrossRef]
- Chub, A.; Vinnikov, D.; Kosenko, R.; Liivik, E.; Galkin, I. Bidirectional DC–DC Converter for Modular Residential Battery Energy Storage Systems. IEEE Trans. Ind. Electron. 2020, 67, 1944–1955. [Google Scholar] [CrossRef]
- Sabry, A.H.; Shallal, A.H.; Hameed, H.S.; Ker, P.J. Compatibility of household appliances with DC microgrid for PV systems. Heliyon 2020, 6, e05699. [Google Scholar] [CrossRef] [PubMed]
- Elvira, D.G.; Blaví, H.V.; Pastor, À.C.; Salamero, L.M. Efficiency Optimization of a Variable Bus Voltage DC Microgrid. Energies 2018, 11, 3090. [Google Scholar] [CrossRef]
- Dong, D.; Cvetkovic, I.; Boroyevich, D.; Zhang, W.; Wang, R. Mattavelli. Grid-Interface Bidirectional Converter for Residential DC Distribution Systems—Part One: High-Density Two-Stage Topology. IEEE Trans. Power Electron. 2013, 28, 1655–1666. [Google Scholar] [CrossRef]
- Teodosescu, P.D.; Pintilie, L.N.; Iuora, A.M.; Salcu, S.I.; Bojan, M. Micro-Grid Has Bidirectional Sources which Inject or Absorb Energy from Micro-Grid Based on Power converters with Two Conversion Stages, in which Alternating Current Consumers and Direct Current Consumers Absorb Energy. Available online: https://www.webofscience.com/wos/diidw/full-record/DIIDW:202073761E (accessed on 7 September 2023).
- Nicolae, P.L. Research Aimed at Electricity Management in Electronic Systems with Renewable Sources. Ph.D. Thesis, Technical University of Cluj-Napoca, Cluj-Napoca, Romania, 2023. under press.
- Moussa, S.; Ghorbal, M.J.-B.; Slama-Belkhodja, I. Bus voltage level choice for standalone residential DC nano grid. Sustain. Cities Soc. 2019, 46, 101431. [Google Scholar] [CrossRef]
- Li, T.; Ji, Z.C. Intelligent inverse control to maximum power point tracking control strategy of wind energy conversion system. In Proceedings of the 2011 Chinese Control and Decision Conference (CCDC), Mianyang, China, 23–25 May 2011; IEEE: Piscataway Township, NJ, USA, 2011; pp. 970–974. [Google Scholar] [CrossRef]
- Teodosescu, P.D.; Pintilie, L.N.; Iuoras, A.M.; Salcu, S.I.; Bojan, M. Micro-Grid of Variable DC Voltage and Its Control Method—Official Bulletin of Industrial Property. RO134348A0. Available online: https://osim.ro/wp-content/uploads/Publicatii-OSIM/BOPI-Inventii/2020/bopi_inv_07_2020.pdf (accessed on 7 September 2023).
- Anand, S.; Fernandes, B.G. Optimal voltage level for DC microgrids. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 3034–3039. [Google Scholar] [CrossRef]
- Mallik, A.; Khaligh, A. Maximum Efficiency Tracking of an Integrated Two-Staged AC–DC Converter Using Variable DC-Link Voltage. IEEE Trans. Ind. Electron. 2018, 65, 8408–8421. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, X.; Zhao, M.; Wang, L.; Shen, X. 30–300 mV input, ultra-low power, self-startup DC-DC boost converter for energy harvesting system. In Proceedings of the 2012 IEEE Asia Pacific Conference on Circuits and Systems, Kaohsiung, Taiwan, 2–5 December 2012; pp. 432–435. [Google Scholar] [CrossRef]
- Suciu, V.M.; Salcu, S.I.; Pintilie, L.N.; Teodosescu, P.D.; Mathe, Z. Theoretical efficiency analysis of a buck-boost converter for wide voltage range operation. In Proceedings of the 2018 10th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Iasi, Romania, 28–30 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Mulligan, M.D.; Broach, B.; Lee, T.H. A constant-frequency method for improving light-load efficiency in synchronous buck converters. IEEE Power Electron. Lett. 2005, 3, 24–29. [Google Scholar] [CrossRef]
- Zhou, X.; Donati, M.; Amoroso, L. Improved light-load efficiency for synchronous rectifier voltage regulator module. IEEE Trans. Power Electron. 2000, 15, 826–834. [Google Scholar] [CrossRef]
- PID ‘Proportional, Integral, and Derivative’ Control Theory. Crystal Instruments, 24 August 2020. Available online: https://www.crystalinstruments.com/blog/2020/8/23/pid-control-theory (accessed on 10 July 2023).
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y.; Pawar, S.N. A review of PID control, tuning methods and applications. Int. J. Dyn. Control. 2021, 9, 818–827. [Google Scholar] [CrossRef]
- Omar, O.A.; Marei, M.I.; Attia, M.A. Comparative Study of AVR Control Systems Considering a Novel Optimized PID-Based Model Reference Fractional Adaptive Controller. Energies 2023, 16, 830. [Google Scholar] [CrossRef]
- Alghamdi, S.; Sindi, H.F.; Rawa, M.; Alhussainy, A.A.; Calasan, M.; Micev, M.; Ali, Z.M.; Abdel Aleem, S.H. Optimal PID Controllers for AVR Systems Using Hybrid Simulated Annealing and Gorilla Troops Optimization. Fractal Fract. 2023, 6, 682. [Google Scholar] [CrossRef]
- Ozgenc, B.; Ayas, M.S.; Altas, I.H. Performance improvement of an AVR system by symbiotic organism search algorithm-based PID-F controller. Neural Comput. Appl. 2022, 34, 7899–7908. [Google Scholar] [CrossRef]
- Mohd Tumari, M.Z.; Ahmad, M.A.; Suid, M.H.; Hao, M.R. An Improved Marine Predators Algorithm-Tuned Fractional-Order PID Controller for Automatic Voltage Regulator System. Fractal Fract. 2023, 7, 561. [Google Scholar] [CrossRef]
- Erickson, R.W. Maksimović, Fundamentals of Power Electronics; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Simion, E. Electrotehnică—Manual Pentru Subingineri. In Manuale Pentru Electrotehnică Generală; no. 12000 Ex SP.; Editura Didactică și Pedagogică: Bucuresti, Romania, 1977; Volume 1. [Google Scholar]
- Useful Applications for Electronic Loads (2) Non-Linear Modes—KIKUSUI AMERICA, INC. Available online: https://kikusui.co.jp/ (accessed on 24 June 2023).
- Figueiredo, R.E.; Monteiro, V.; Afonso, J.A.; Pinto, J.G.; Salgado, J.A.; Cardoso, L.A.L.; Nogueira, M.; Abreu, A.; Afonso, J.L. Efficiency Comparison of Different DC-DC Converter Architectures for a Power Supply of a LiDAR System. In Proceedings of the Sustainable Energy for Smart Cities: Second EAI International Conference, SESC 2020, Viana do Castelo, Portugal, 4 December 2020; Springer International Publishing: Cham, Switzerland, 2021; pp. 97–110. [Google Scholar] [CrossRef]
- Guy, P. Efficiency Calculations for Power Converters. Industrial and Medical Power Supplies. TDK—Lambda Americas, 5 September 2012. Available online: https://www.us.lambda.tdk.com (accessed on 7 September 2023).
- Wang, B.; Hu, Q.; Wang, Z. A High-Efficiency Double DC–DC Conversion System for a Fuel Cell/Battery Hybrid Power Propulsion System in Long Cruising Range Underwater Vehicles. Energy Fuels 2020, 34, 8872–8883. [Google Scholar] [CrossRef]
- Taufik, D. Practical Design of Buck Converter. In Proceedings of the 2008 2nd IEEE International Conference on Power and Energy PECon 2008, Johor Bahru, Malaysia, 1–3 December 2008. [Google Scholar]
- Chen, D.; Xu, L.; Yao, L. DC Voltage Variation Based Autonomous Control of DC Microgrids. IEEE Trans. Power Deliv. 2013, 28, 637–648. [Google Scholar] [CrossRef]
- Zhang, X. Impedance Control and Stability of DC/DC Converter Systems. Ph.D. Thesis, Department of Automatic Control and Systems Engineering, Faculty of Engineering, University of Sheffield, Sheffield, UK, 2016. [Google Scholar]
- Ginell, T. Why a Perfectly Stable Switch-Mode Power Supply May Still Oscillate Due to Negative Resistance. Analog Dialogue. Analog Devices. Published on March 2023. Available online: https://www.analog.com/en/analog-dialogue/raqs/raq-issue-211.html (accessed on 7 September 2023).
- MathWorks Inc. Behavioral Model of Power Converter. Average models of DC-DC Converters, SimScape Fundamentals, Published in 2022 Updated in 2023. Available online: https://www.mathworks.com/help/sps/ref/dcdcconverter.html (accessed on 7 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).