Phasor Measurement Unit Assisted Inverter—A Novel Approach for DC Microgrids Performance Enhancement
Abstract
1. Introduction
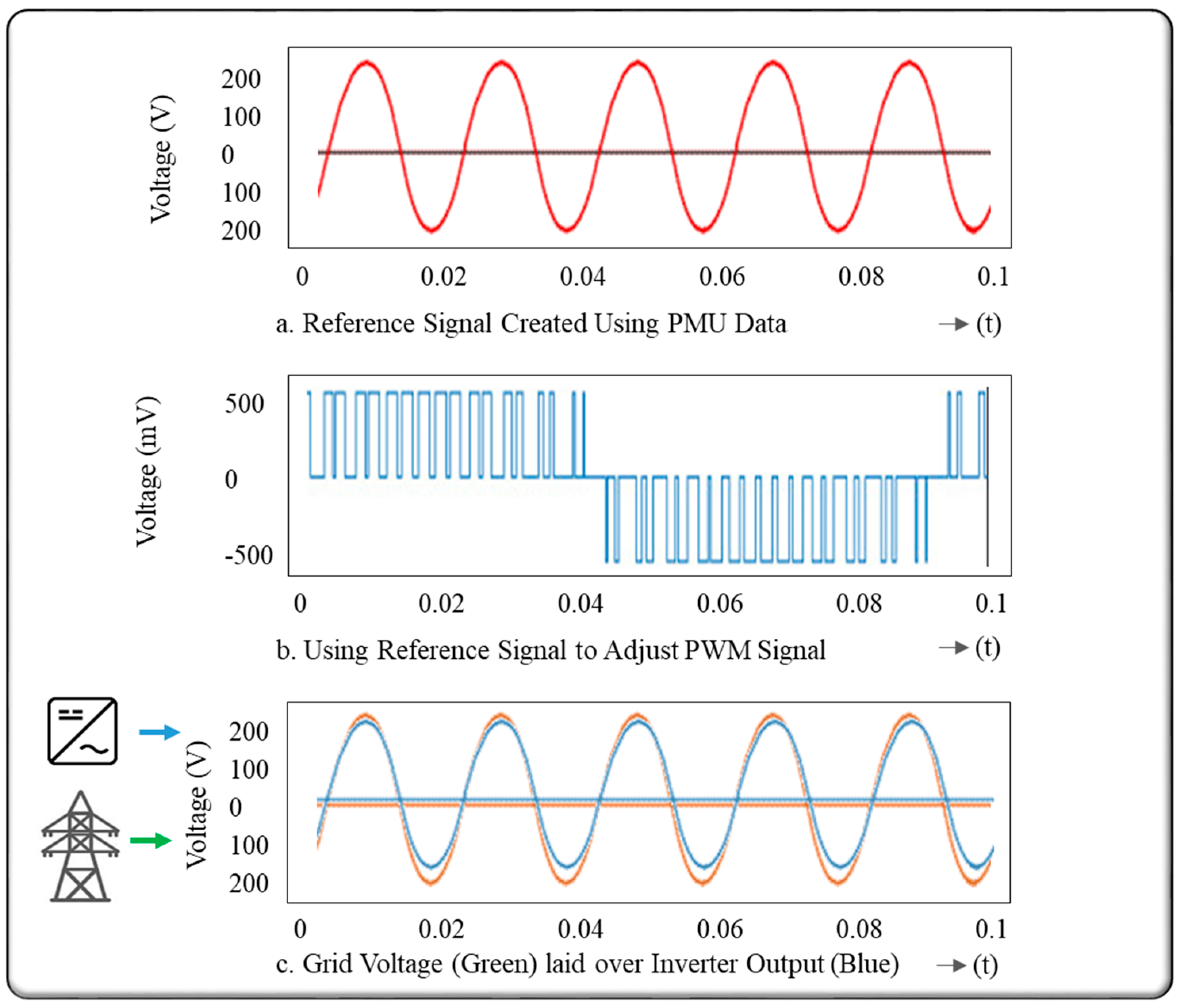
1.1. Initial Synchronization of DC Microgrid with the Utility’s AC Grid
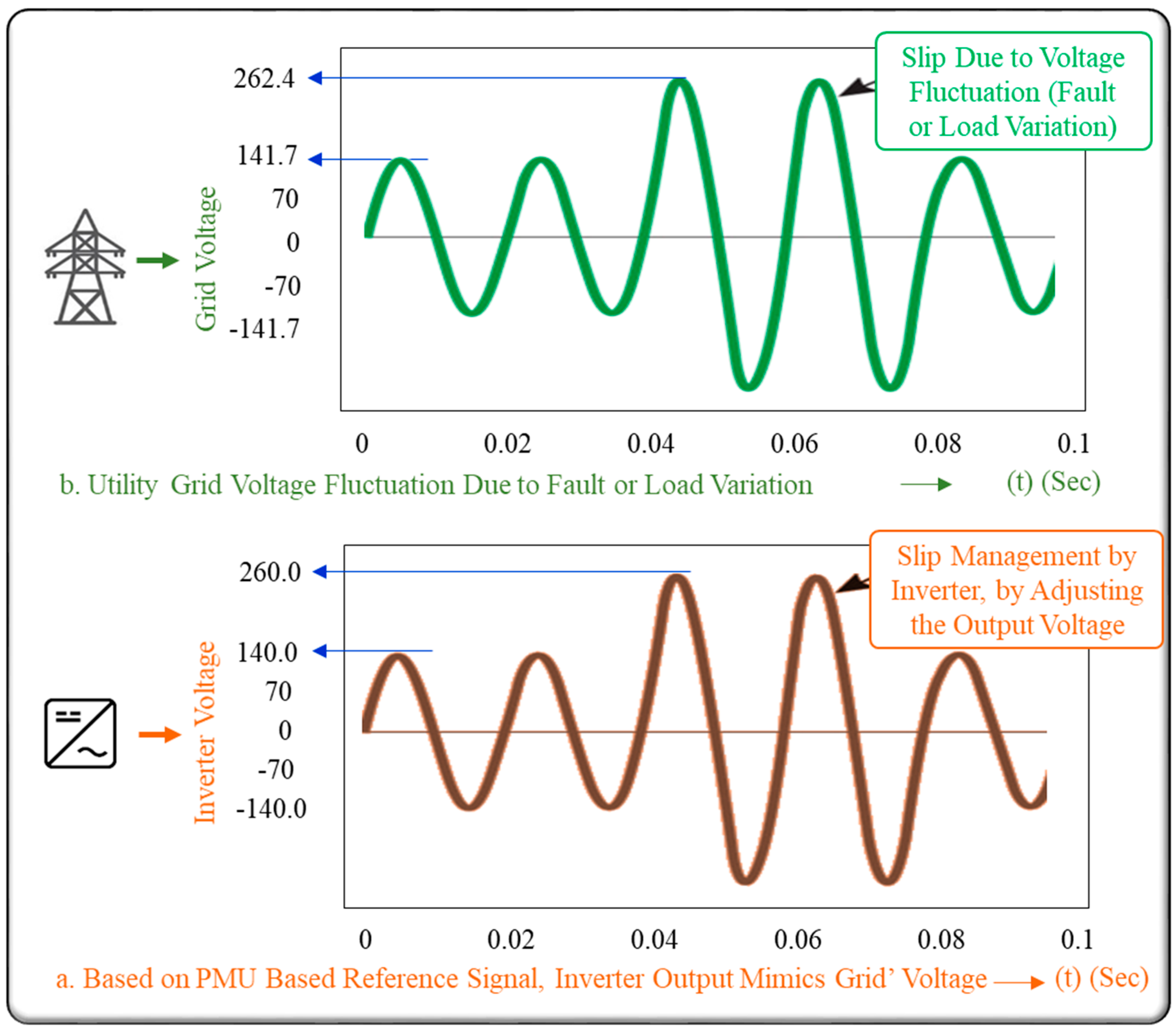
1.2. Slip Management during Connected Mode Operation
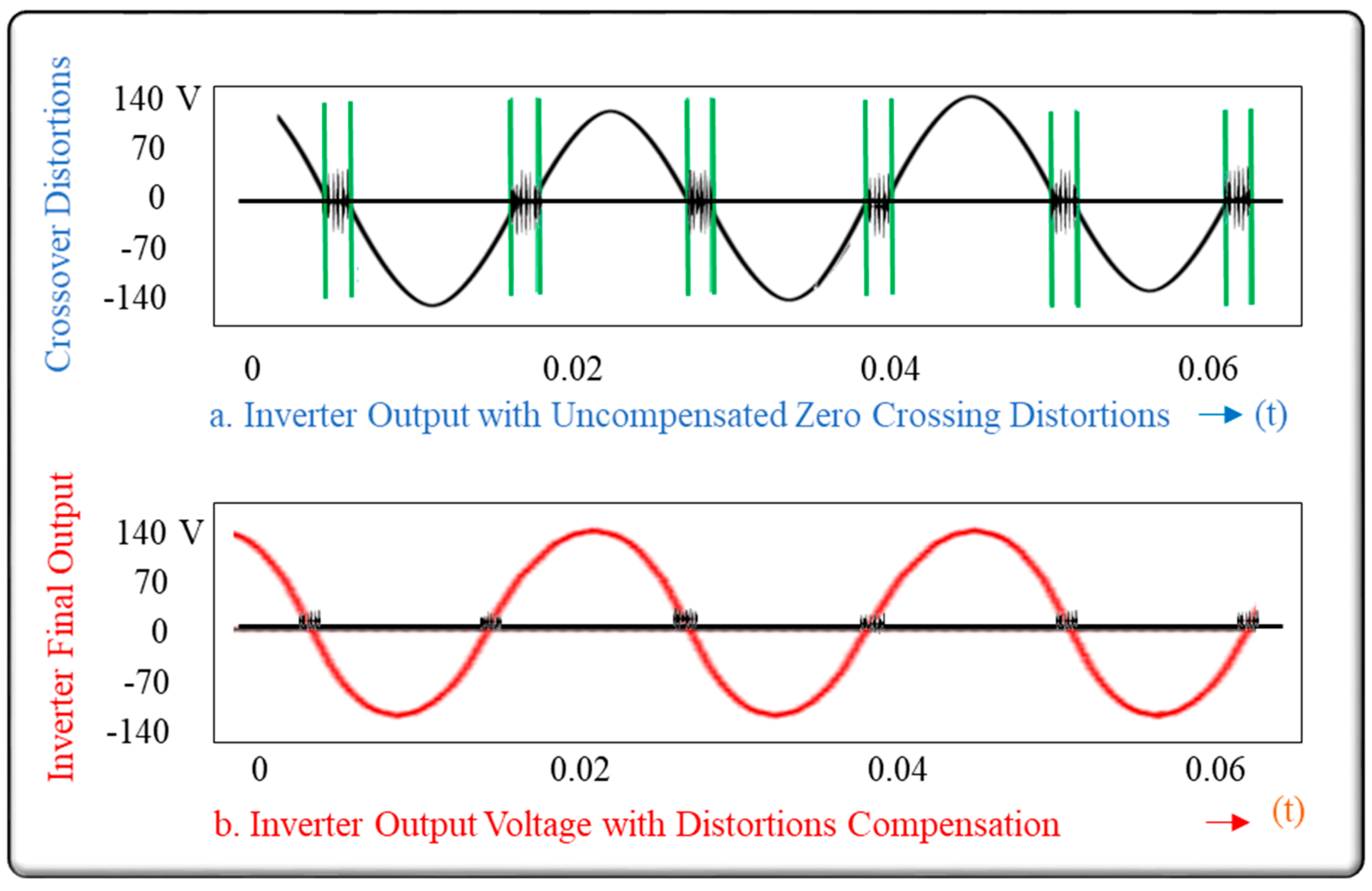
1.3. Production of Distortion-Free, Pure Sine Wave
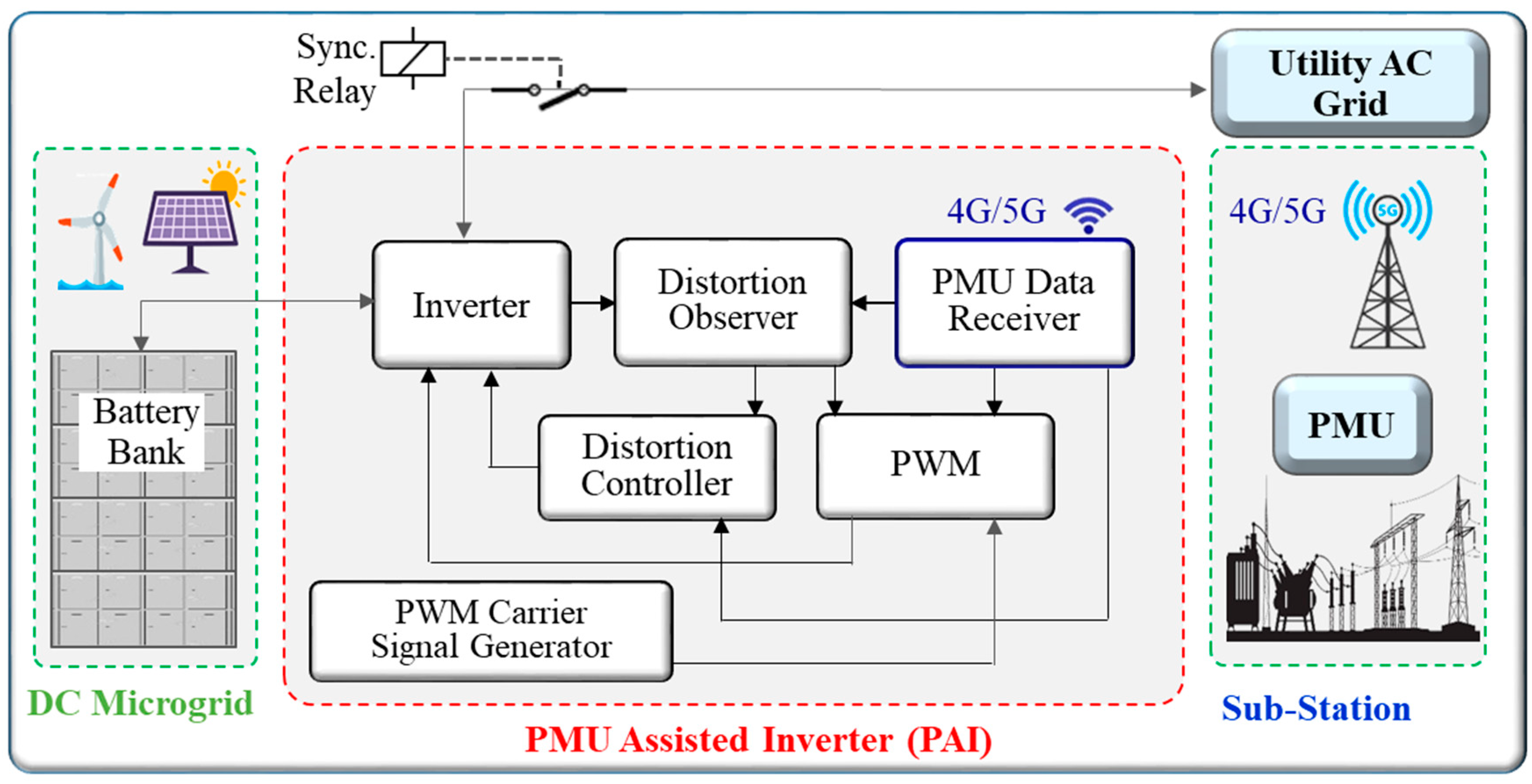
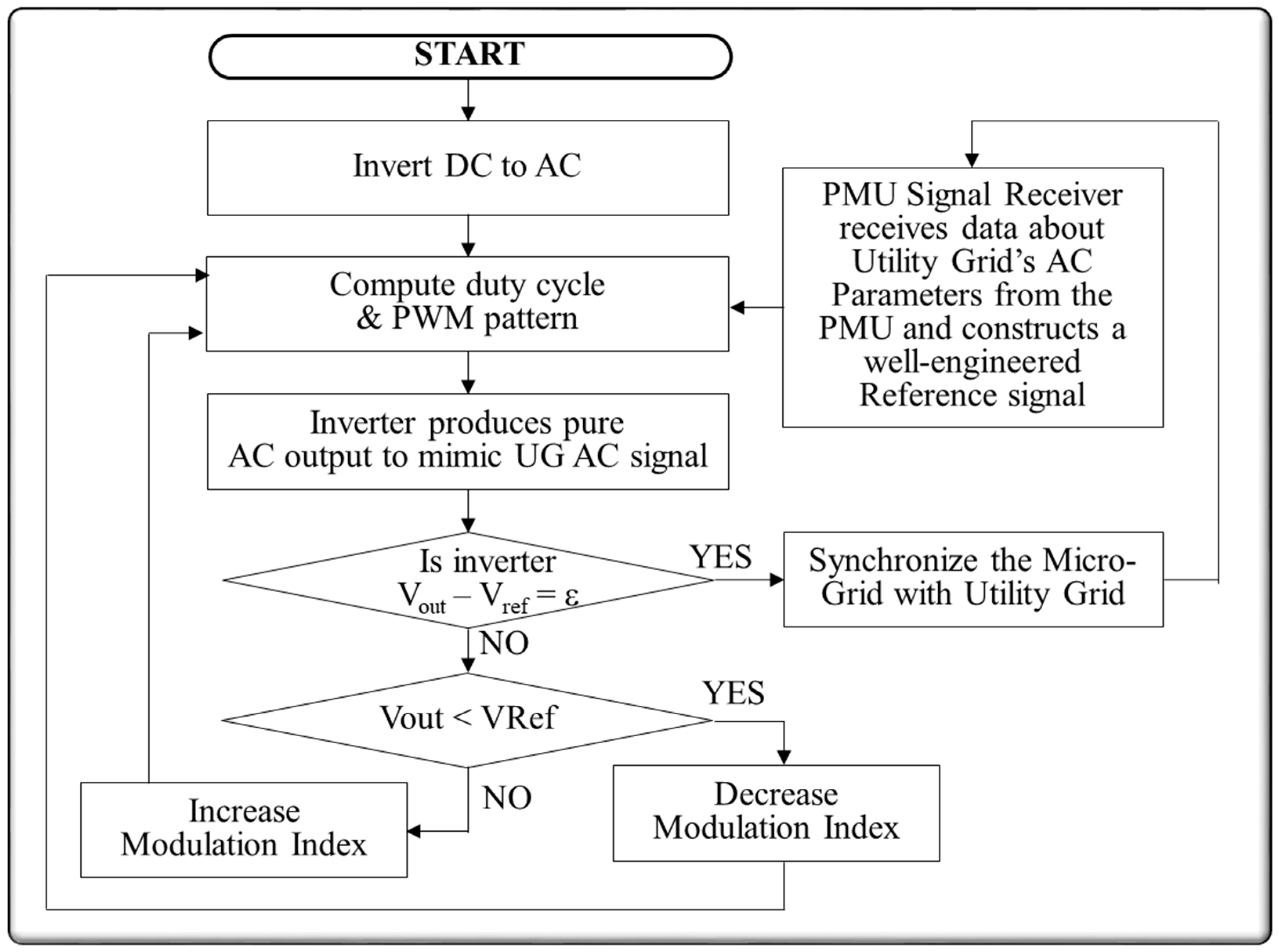
2. Description of Proposed Work
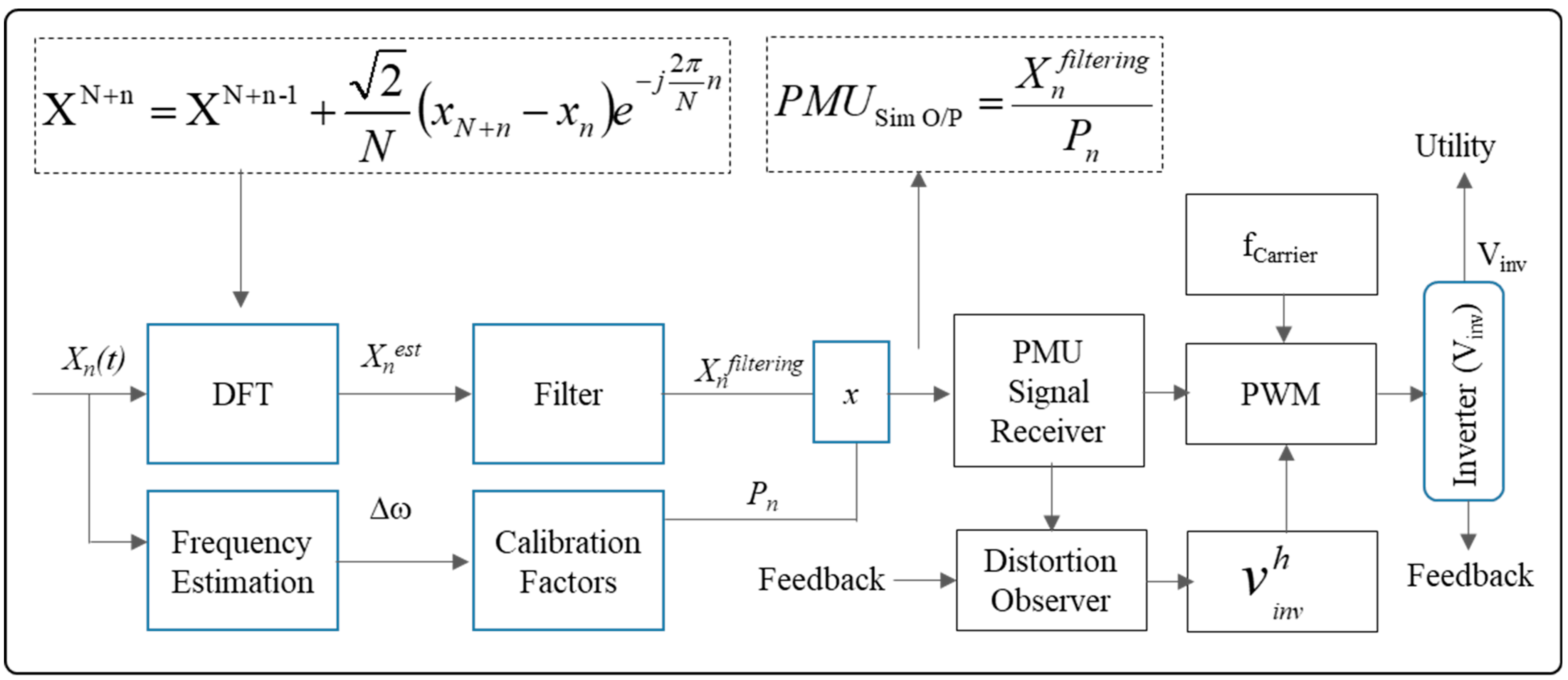
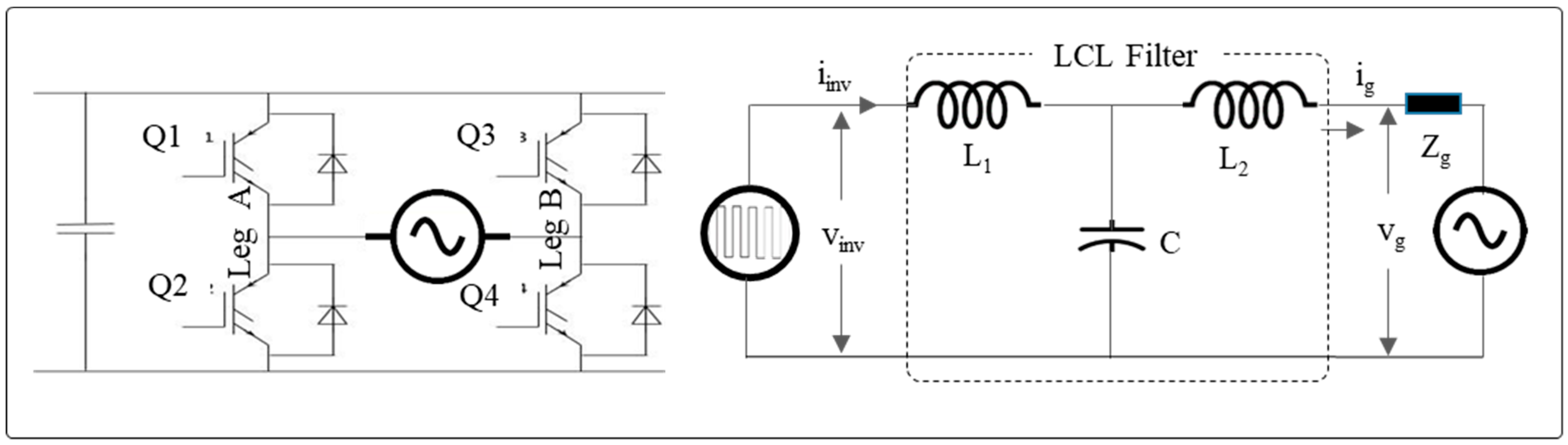
3. Discussion: Simulation and Mathematical Analysis
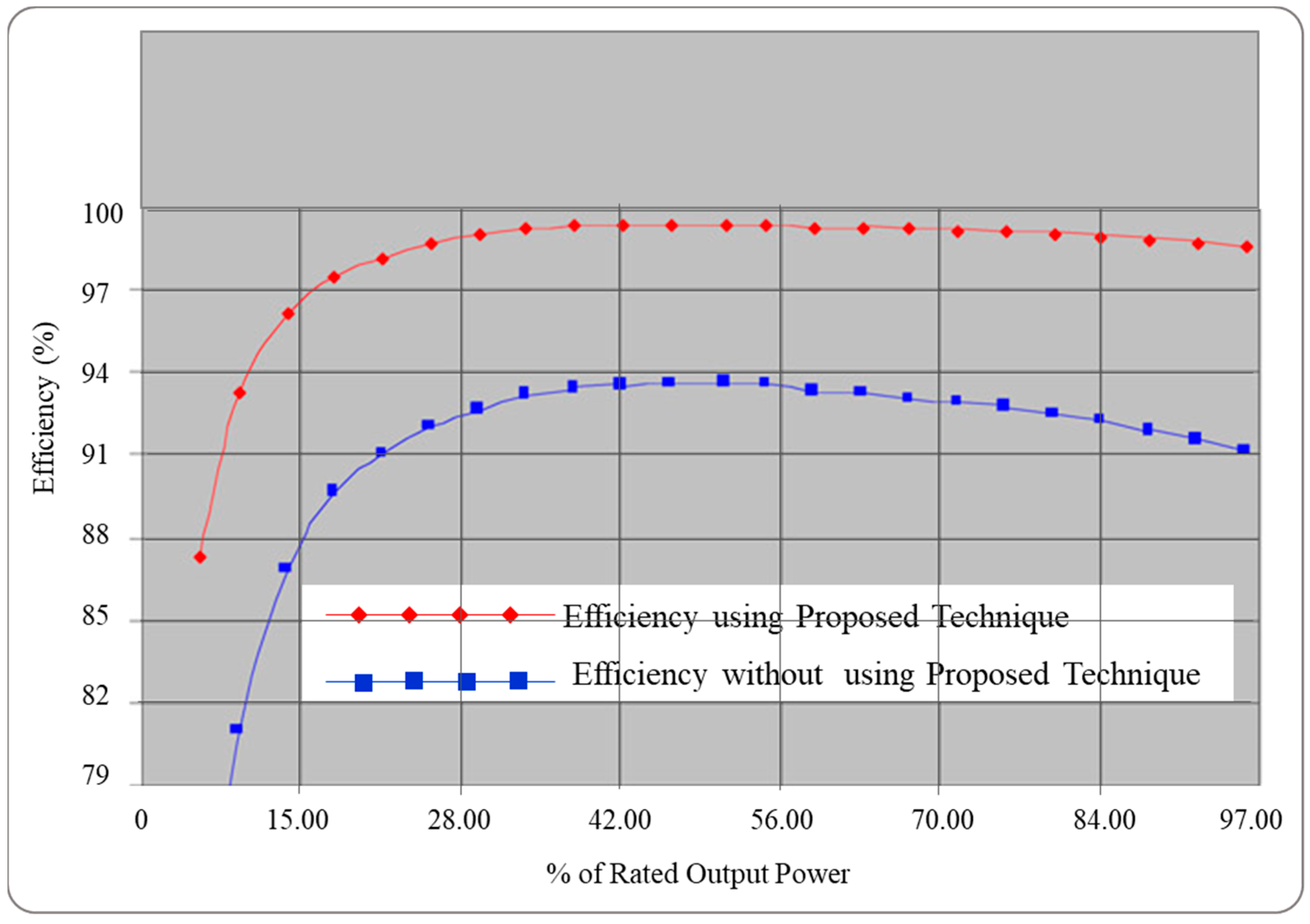
Inverter Efficiency
4. Conclusions
5. Future Work
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Inverter Pspice Script
References
- Palaniappan, K. A Viable Residential DC Microgrid for Low-Income Communities, Ph.D. Thesis Submitted to the University of Wisconsin-Milwaukee. 2019. Available online: https://dc.uwm.edu/cgi/viewcontent.cgi?article=3238&context=etd (accessed on 20 September 2020).
- Balaguer, I.J.; Lei, Q.; Yang, S.; Supatti, U.; Peng, F.Z. Control for grid-connected and intentional islanding operations of distributed power generation. IEEE Trans. Ind. Electron. 2011, 58, 147–157. [Google Scholar] [CrossRef]
- Shaaban, A.; Thomas, J.; Mostafa, R. Design and Implementation of a Single Phase SPWM Inverter Based Microcontroller for Wind Energy Conversion Systems. Int. J. Syst. Appl. Eng. Dev. 2017, 11, 291–296. [Google Scholar]
- Toulabi, M.R.; Shroei, M.; Ranjbar, A.M. Robust Analysis and Design of Power System Load Frequency Control using the Kharitonov’s Theorem. Int. J. Electr. Power Energy Syst. 2014, 55, 51–58. [Google Scholar] [CrossRef]
- Spitsa, V.; Kuperman, A.; Weiss, G.; Rabinovici, R. Design of a Robust Voltage Controller for an Induction Generator in an Autonomous Power System Using a Genetic Algorithm. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 3475–3481. [Google Scholar]
- de Souza, W.A.; Teixeira, M.C.M.; Santim, M.P.A.; Cardim, R.; Assunção, E. Robust Switched Control Design for Nonlinear Systems Using Fuzzy Models; Mathematical Problems in Engineering; Hindawi Publishing Co.: London, UK, 2014; pp. 1–11. [Google Scholar]
- Evanczuk, S. Synchronizing Small-Scale PV Systems with the Grid, 2015–09. Available online: www.digikey.com/en/articles/synchronizing-small-scale-pv-systems-with-the-grid. (accessed on 20 September 2020).
- Fuad, K.S.; Hossain, E. Performance of grid-voltage synchronization algorithms based on frequency-and phase-locked loop during severe grid fault conditions. In Proceedings of the 3rd International Conference on Electrical Engineering and Information Communication Technology (ICEEICT)], Dhaka, Bangladesh, 22–24 September 2016. [Google Scholar] [CrossRef]
- Jin, C.; Gao, M.; Lv, X.; Chen, M. A Seamless Transfer Strategy of Islanded and Grid-connected Mode Switching for Microgrid based on Droop Control. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Raleigh, NC, USA, 15–20 September 2012; pp. 969–973. [Google Scholar]
- Begovic, M.M.; Djuric, P.M.; Dunlap, S.; Phadke, A.G. Frequency Tracking in Power Networks in the Presence of Harmonics. IEEE Trans. Power Deliv. 1993, 8, 480–486. [Google Scholar] [CrossRef]
- Yang, J.-Z.; Liu, C.-W. A Precise Calculation of Power System Frequency and Phasor. IEEE Trans. Power Deliv. 2000, 15, 494–499. [Google Scholar] [CrossRef]
- Cho, C.; Kim, S.K.; Jeon, J.H.; Kim, S. New Ideas for a Soft Synchronizer Applied to CHP Cogeneration. IEEE Trans. Power Deliv. 2011, 26, 11–26. [Google Scholar] [CrossRef]
- Bellini, A.; Bifaretti, S.; Giannini, F. A Robust Synchronization Method for Centralized Microgrids. IEEE Trans. Ind. Appl. 2014, 99, 4587–4594. [Google Scholar]
- Giraldo, J.; Mojica-Nava, E.; Quijano, N. Synchronization of Isolated Microgrids with a Communication Infrastructure using Energy Storage Systems. Int. J. Electr. Power Energy Syst. 2014, 63, 71–82. [Google Scholar] [CrossRef]
- Ahshan, R.; Saleh, S.A.; Al-Badi, A. Performance Analysis of a Dq Power Flow-Based Energy Storage Control System for Microgrid Applications. IEEE Access 2020, 8, 178706–178721. [Google Scholar] [CrossRef]
- Choi, J.W.; Sul, S.K. New dead time compensation eliminating zero current clamping in voltage-fed PWM inverter. In Proceedings of the 1994 IEEE Industry Applications Society Annual Meeting, Denver, CO, USA, 2–6 October 1994; Volume 2, pp. 977–984. [Google Scholar]
- Zhang, J.; Fang, L. An accurate approach of dead-time compensation for three-phase DC/AC inverter. In Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009; pp. 2929–2934. [Google Scholar]
- Ji, Y.; Yang, Y.; Zhou, J.; Ding, H.; Guo, X.; Padmanaban, S. Control Strategies of Mitigating Dead-time Effect on Power Converters. Electron. J. 2019, 8, 196. [Google Scholar] [CrossRef]
- Zhou, H.W.; Wen, X.H.; Zhao, F.; Zhang, J.; Guo, X.H. A novel adaptive dead-time compensation strategy for VSI. Proc. CSEE 2011, 31, 26–32. [Google Scholar]
- Song, C.H.; Diao, N.Z.; Xue, Z.W.; Sun, X.R.; Guan, J. Tri-carrier sinusoidal pulse-width modulation without dead-time effects for converters. IET Power Electron. 2015, 8, 1941–1951. [Google Scholar] [CrossRef]
- Ikegami, S.; Hoshi, N.; Haruna, J. Experimental verification of dead-time compensation scheme for pulse width modulation scheme on six-switch two three-phase out put inverter. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 1420–1424. [Google Scholar]
- Bespal, K.; Savarovsky, V.J.; Stepin, V. Method for measuring pulse width, which is less than the dead-time of measurement instrument. In Proceedings of the 2012 13th Biennial Baltic Electronics Conference, Tallinn, Estonia, 3–5 October 2012; pp. 311–314. [Google Scholar]
- Ogawa, M.; Ogasawara, S.; Takemoto, M. A feedback-type dead-time compensation method for high-frequency PWM inverter-Delay and pulse width characteristics. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 100–105. [Google Scholar]
- Weerakoon, D.B.R.; Sandaruwan, B.L.L.; De Silva, R.T.T.; Abeyratne, S.G.; Rathnayake, D.B. A novel dead-time compensation scheme for PWM VSI drives. In Proceedings of the 2016 IEEE International Conference on Information and Automation for Sustainability (ICIAfS), Galle, Sri Lanka, 16–19 December 2016; pp. 1–6. [Google Scholar]
- Lee, C.-T.; Chu, C.-C.; Cheng, P.-T. A New Droop Control Method for the Autonomous Operation of Distributed Energy Resource Interface Converters. IEEE Trans. Power Electron. 2013, 28, 1980–1993. [Google Scholar] [CrossRef]
- Sadrul Islam, A.K.M.; Rahman, M.M.; Mondal, M.A.H.; Alam, F. Hybrid energy system for St. Martin island, Bangladesh: An optimized model. Procedia Eng. 2012, 49, 179–188. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Iravani, M.R. A Method for Synchronization of Power Electronic Converters in Polluted and Variable-Frequency Environments. IEEE Trans. Power Syst. 2004, 19, 1263–1270. [Google Scholar] [CrossRef]
- Saleh, S.A.; Ahshan, R. Resolution-Level-Controlled WM Inverter for PMG-Based Wind Energy Conversion System. IEEE Trans. Ind. Appl. 2012, 48, 750–763. [Google Scholar] [CrossRef]
- Peter, A.K.; Mark, J.M.H.; Jansen, J. Zero-Crossing Distortion in Grid-Connected PV Inverters. IEEE Trans. Ind. Electron. 2005, 52, 558–565. [Google Scholar] [CrossRef]
- Yaqub, R.; Tariq, A.; Cao, Y. A Smart Solution for Fair Value Compensation (FVC) in EV-Batteries Based Mobile Microgrid. In Proceedings of the 2012 10th International Conference on Frontiers of Information Technology, Islamabad, Pakistan, 17–19 December 2012. [Google Scholar]
- Dotta, D.; Chow, J.H.; Vanfretti, L.; Almas, M.S.; Agostini, M.N. A MATLAB-based PMU simulator. In Proceedings of the IEEE Conference on Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar] [CrossRef]
- Synchronizing and Synchronizing Equipment. Available online: http://www.o-t-s.com/synchronizing.htm (accessed on 13 December 2020).
- An Industry and National Laboratory collaborative to Improve Photovoltaic Performance Modeling. Available online: https://pvpmc.sandia.gov/modeling-steps/dc-to-ac-conversion/cec-inverter-test-protocol/ (accessed on 13 December 2020).
- Application Report Voltage Fed Full Bridge DC-DC and DC-AC Converter for High-Frequency Inverter Using C2000. Available online: https://www.ti.com/lit/an/sprabw0d/sprabw0d.pdf?ts=1625357422076 (accessed on 20 September 2020).
- Xu, Y.; Li, H.; Rizy, D.; Li, F.; Kueck, J. Instantaneous active and nonactive power control of distributed energy resources with a current limiter. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010. [Google Scholar] [CrossRef]
- Unamuno, E.; Barrena, J.A. Hybrid ac/dc Microgrids—Part I: Review and Classification of Topologies. August 2015. Available online: https://doi.org/10.1016/j.rser.2015.07.194 (accessed on 20 September 2020).
- Nguyen, M.H.; Becan, A.F.; Harvey, B.W. “Active Filtering Using Wind Turbine Generator”, a thesis submitted to Worcester Polytechnic Institute (WPI), April 2015. Available online: https://digital.wpi.edu/concern/student_works/mp48sf48b. (accessed on 20 September 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yaqub, R. Phasor Measurement Unit Assisted Inverter—A Novel Approach for DC Microgrids Performance Enhancement. Electricity 2021, 2, 330-341. https://doi.org/10.3390/electricity2030020
Yaqub R. Phasor Measurement Unit Assisted Inverter—A Novel Approach for DC Microgrids Performance Enhancement. Electricity. 2021; 2(3):330-341. https://doi.org/10.3390/electricity2030020
Chicago/Turabian StyleYaqub, Raziq. 2021. "Phasor Measurement Unit Assisted Inverter—A Novel Approach for DC Microgrids Performance Enhancement" Electricity 2, no. 3: 330-341. https://doi.org/10.3390/electricity2030020
APA StyleYaqub, R. (2021). Phasor Measurement Unit Assisted Inverter—A Novel Approach for DC Microgrids Performance Enhancement. Electricity, 2(3), 330-341. https://doi.org/10.3390/electricity2030020




