Optimized Strategic Planning of Future Norwegian Low-Voltage Networks with a Genetic Algorithm Applying Empirical Electric Vehicle Charging Data
Abstract
1. Introduction
- Simultaneity factors and equivalent peak loads of Norwegian households are derived from a large dataset to serve as input for LV network planning purposes of network operators in Norway, for different EV shares and for status quo and future EV charging capacity;
- A novel strategic network planning optimization, combining traditional network reinforcement with novel measures is developed and applied to calculate the minimal reinforcement costs of three representative rural Norwegian networks.
2. Materials and Methods
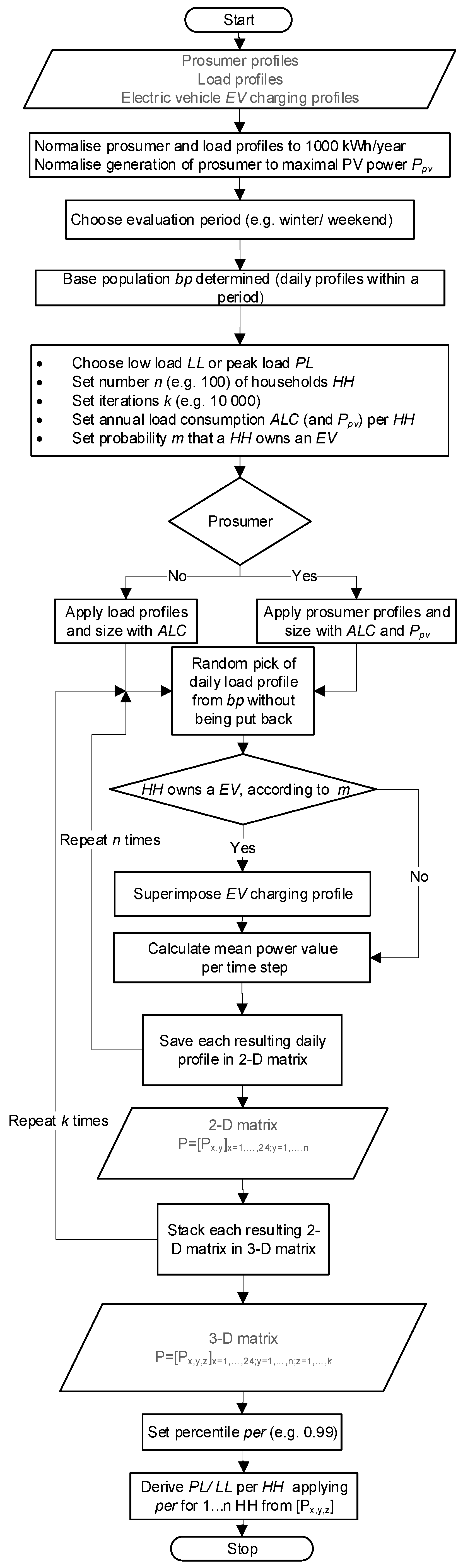
2.1. Stochastic Analysis of Smart Meter Data
2.2. A Genetic Algorithm for Strategic Network Planning
3. Results and Discussion
- quantifying the hosting capacity of EVs;
- quantifying the optimized network reinforcement costs of a growing EV penetration pathway.
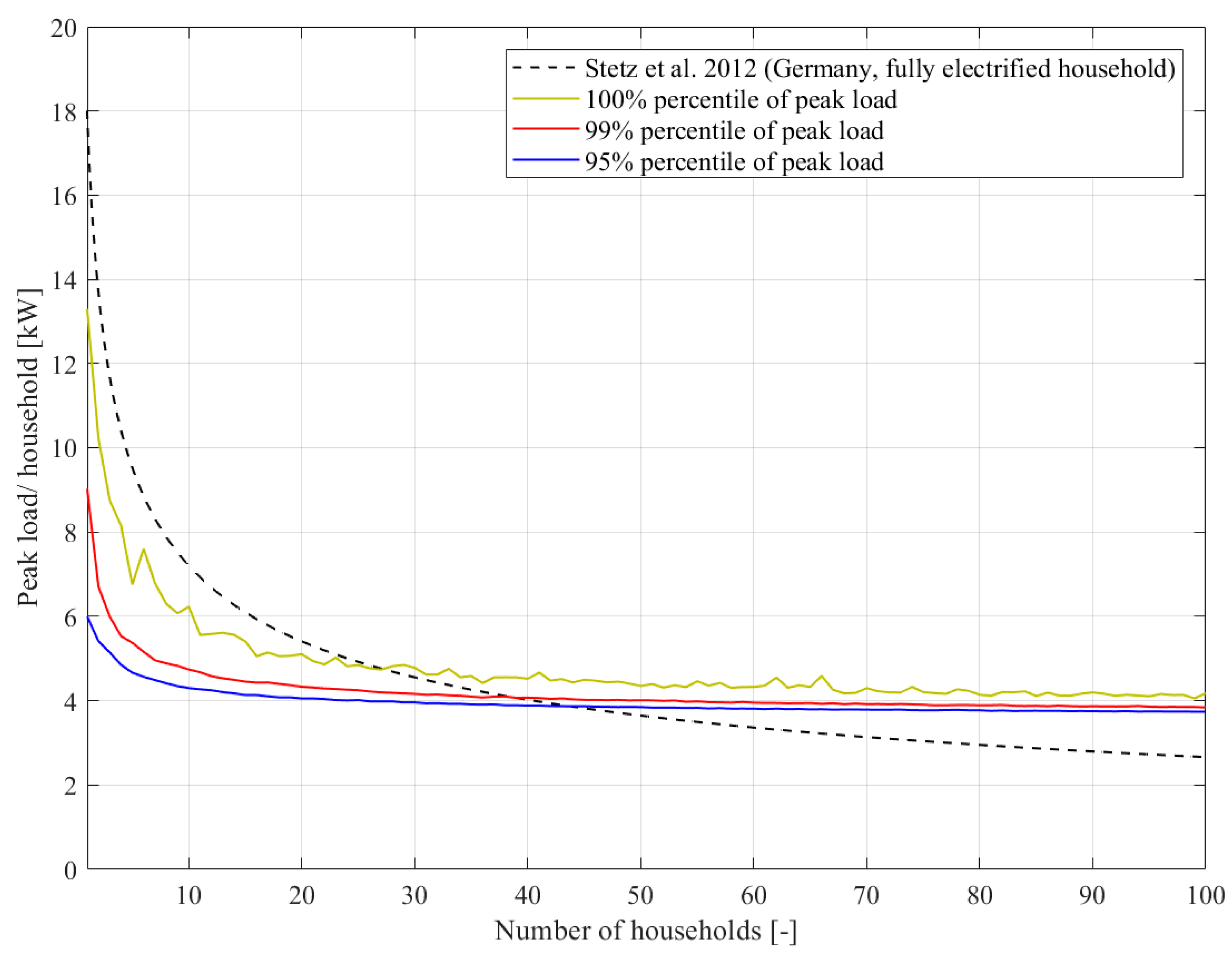
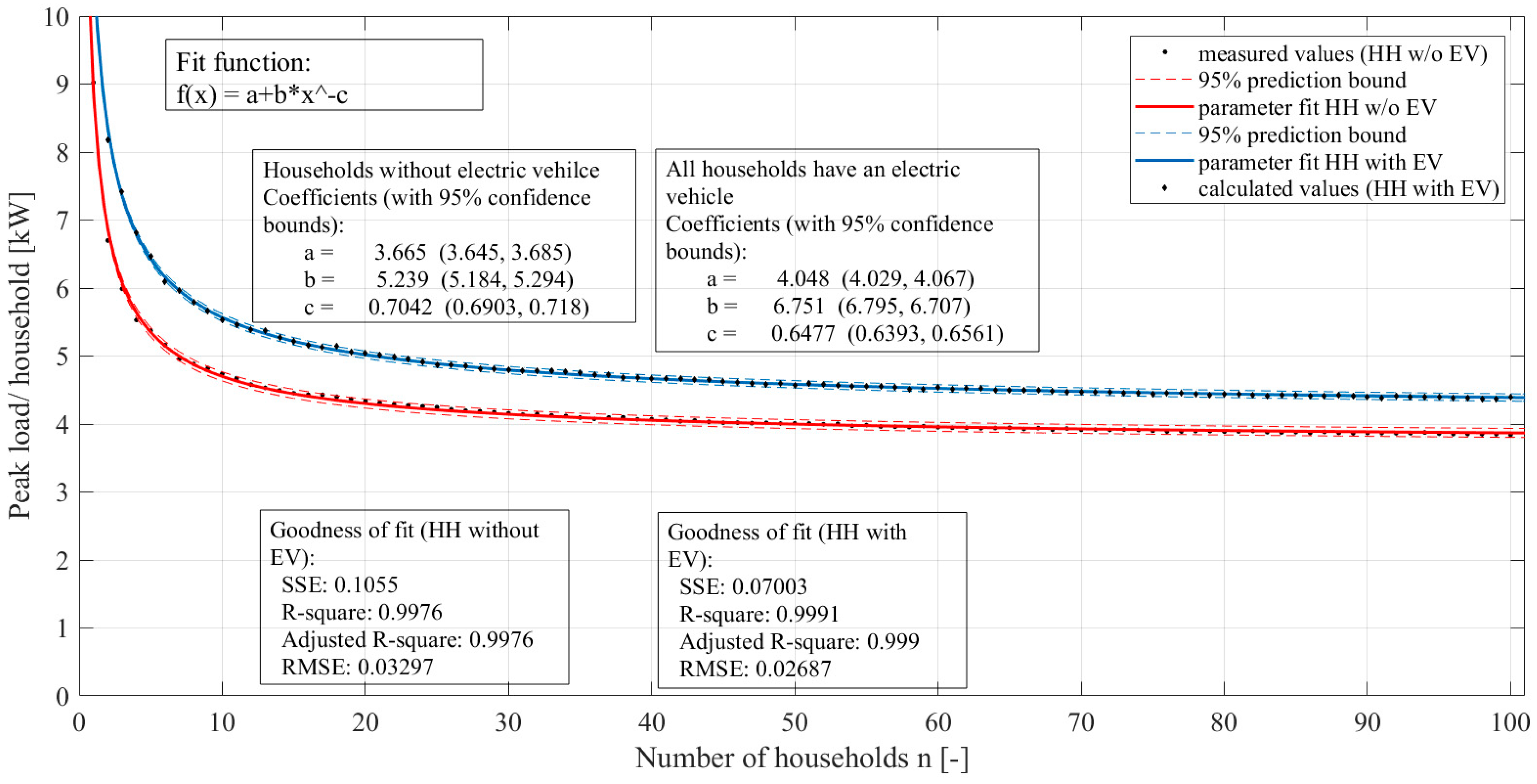
3.1. Calculation of Equivalent Loads and SFs for Households with and without EVs
3.1.1. Equivalent Loads Based on Smart Meter Data of Households without EVs
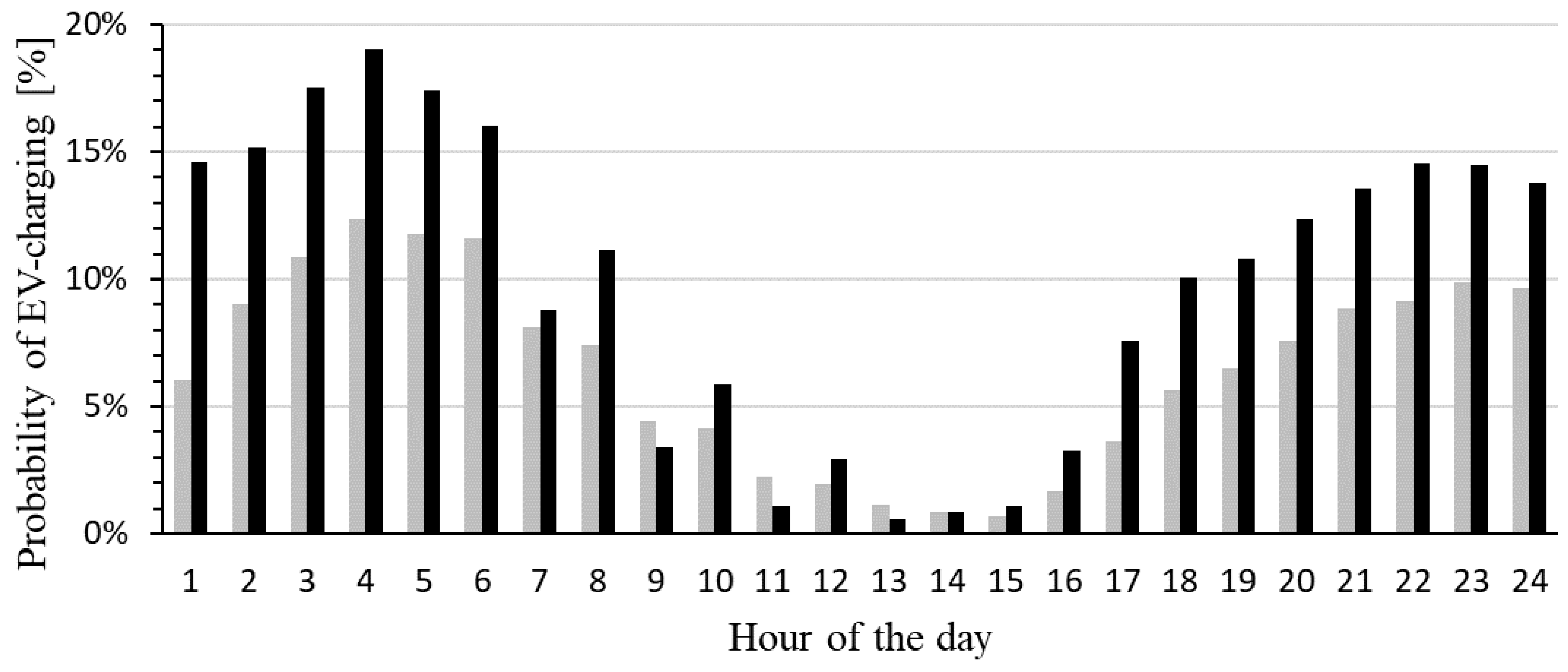
3.1.2. Equivalent Loads Based of Smart Meter Data of Households with EVs
- Charging power: 63% of the EVs are charged with 10 A (2.3 kW), 19% with 16 A (3.38 kW) and 12% with 32 A or more (7.36 kW); assumption: charging power is limited to 7.36 kW in this study for the status quo;
- Daily charging profiles: 12,665 daily charging profiles (1 h steps) are based on the information of the EV owners (database is not public);
- Behavior: 93% of the EVs charge at home; assumption: All electric vehicles charge at home;
- Behavior: 70% of the EVs charge daily; assumption: All electric vehicles are charged daily;
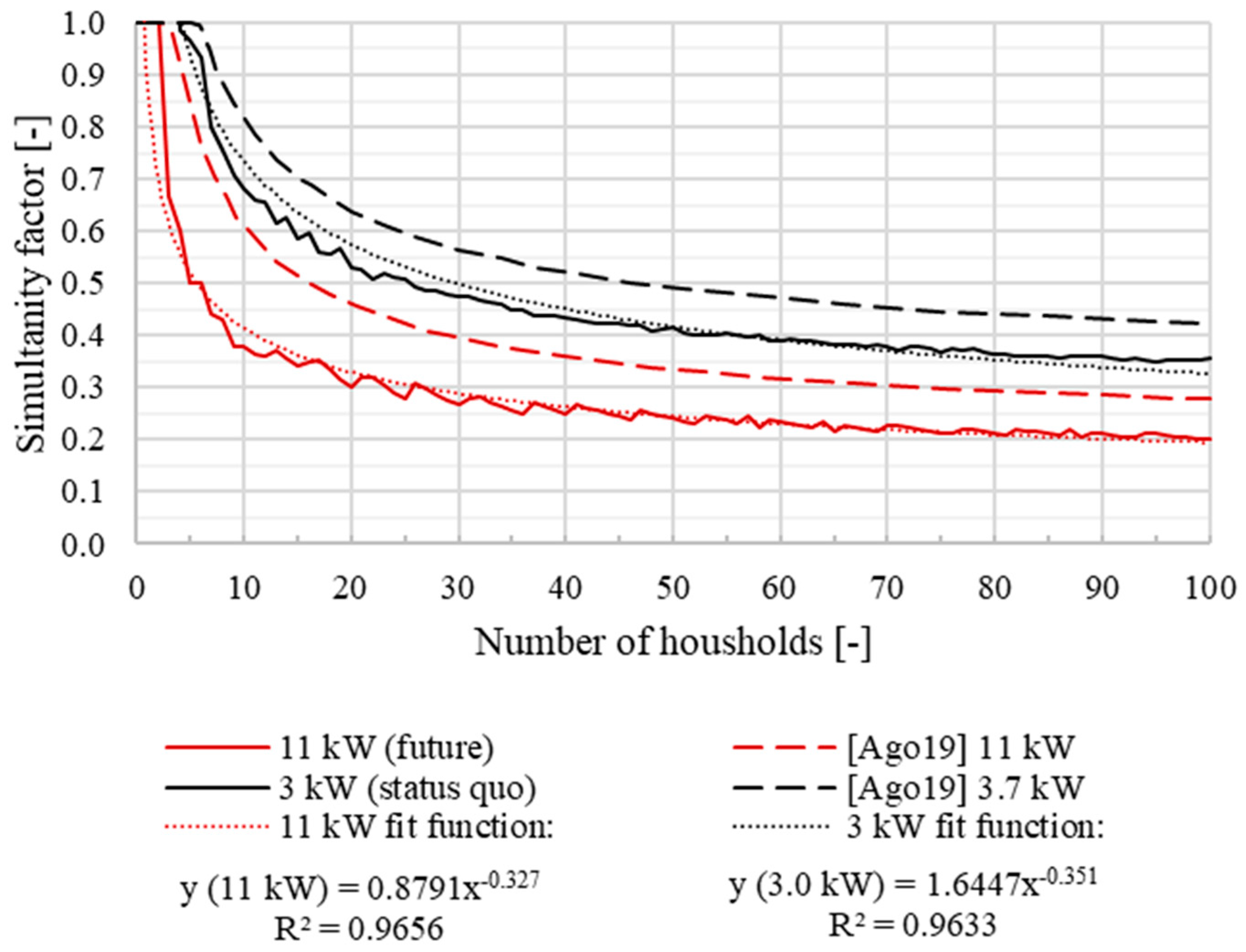
3.1.3. Simultaneity Factors: Status Quo and Possible Future
- in the status quo power charging mix, there is a variety of charging power ranging from 2.3 kW to 7.4 kW, whereas in [22] all EVs charge with 3.7 kW.
3.1.4. Scenario Application and of Input Parameters
3.2. Electric Vehicle Studies Based on Scenarios
3.2.1. Application of EV Scenarios
3.2.2. Planning Results
3.3. Variants of the EV Study
3.3.1. 11 kW Fast Charging and 100% EV Penetration
3.3.2. EV Hosting Capacity
3.4. Summary and Comparison of the Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Notations
| Set of all feeders (starting at LV bus bar) | |
| Set of all nodes | |
| Set of all lines | |
| Set of additional lines | |
| Set of substation upgrades | |
| Set of substation upgrades with conventional transformer | |
| Set of substation upgrades with regulated distribution transformer (RDT) | |
| Base population | |
| Cost of network reinforcement | |
| Cost of installing a line from node to with line type | |
| Cost of upgrading the substation with a transformer of type | |
| Cost of installing a line voltage regulator of type | |
| Aggregated cost of network reinforcement | |
| Feeder | |
| Current running through the line from node to node | |
| Maximum permitted current for the line from node to node | |
| Number of (end customers, genes) | |
| Number of parallel lines of line ij | |
| Number of LVRs in feeder f | |
| Equivalent (active) power | |
| Active power injected at node | |
| Reactive power injected at node | |
| Peak load | |
| Simultaneity factors | |
| Apparent power rating of an LVR | |
| Maximum apparent power loading of an LVR | |
| Apparent power rating of substation transformer | |
| Maximum apparent power loading of substation transformer | |
| Nodal voltage at node | |
| Maximum permitted voltage | |
| Minimum permitted voltage | |
| Nominal voltage of the network | |
| Type (of line, substation upgrade, voltage regulator) |
References
- CIGRE. Technical Brochure 591, Planning and Optimization Methods for Active Distribution Systems; Working Group C6.19. 2014. Available online: https://d1wqtxts1xzle7.cloudfront.net/51777692/2014_CIGRE_Brochure_591_-_Planning_and_Optimization_Methods_for_Active_Distribution_Systems.pdf?1487001402=&response-content-disposition=inline%3B+filename%3DPlanning_and_Optimization_Methods_for_Ac.pdf&Expires=1615802157&Signature=duLYQoc4mTuuQacrt0V-JmI2nCm8FPfClRp7VMHQ~WUb77z-KyeSS00RvENXUN7EFfJvbb-fsu41eQ~buLvNbl-CmoHM7dIeAAbmWpirZPfrCw16xWKbnoMNvbd4iHA3vy-1AF6pTCapKG5VqliNY2sCpIsG54NZGv~lV7IINFgPplDfosjvS82pNlb2se27qPsJDgJmqpRgTy8aeJo6KLRom-XyFx701QJqsWJOrNMR5zhtoPQjA8ITanJJOlvcl12QNzVRcQoc6GiZKdfS6U6gyV8~jJ9ghKbKGBZdT3O2MNCquFRmrYva4rCYoqH3oL-57zU7j1WqVdTPnhGCIg__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZA (accessed on 15 January 2020).
- Patzack, S.; Vennegeerts, H.; Moser, A. Determination of relevant network planning cases. In Proceedings of the 24th International Conference on Electricity Distribution (CIRED), Glasgow, UK, 12–15 June 2017. [Google Scholar]
- Yao, W.; Zhao, J.; Wen, F.; Dong, Z.; Xue, Y.; Xu, Y.; Meng, K. A Multi-Objective Collaborative Planning Strategy for Integrated Power Distribution and Electric Vehicle Charging Systems. IEEE Trans. Power Syst. 2014, 29, 1811–1821. [Google Scholar] [CrossRef]
- Yao, W.; Chung, C.Y.; Wen, F.; Qin, M.; Xue, Y. Scenario-Based Comprehensive Expansion Planning for Distribution Systems Considering Integration of Plug-in Electric Vehicles. IEEE Trans. Power Syst. 2015, 31, 317–328. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Y.; Cheng, K.-W.E. Distribution System Planning Considering Stochastic EV Penetration and V2G Behavior. IEEE Trans. Intell. Transp. Syst. 2020, 21, 149–158. [Google Scholar] [CrossRef]
- da Silva, E.L.; Gil, H.A.; Areiza, J.M. Transmission network expansion planning under an improved genetic algorithm. In Proceedings of the 21st International Conference on Power Industry Computer Applications, Santa Clara, CA, USA, 16–21 May 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 315–321. ISBN 0-7803-5478-8. [Google Scholar]
- Diaz-Dorado, E.; Cidras, J.; Miguez, E. Application of evolutionary algorithms for the planning of urban distribution networks of medium voltage. IEEE Trans. Power Syst. 2002, 17, 879–884. [Google Scholar] [CrossRef]
- Camargo, V.; Lavorato, M.; Romero, R. Specialized genetic algorithm to solve the electrical distribution system expansion planning. In Proceedings of the IEEE Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013; IEEE: Piscataway, NJ, USA, 2013; ISBN 978-1-4799-1303-9. [Google Scholar]
- Ramirez-Rosado, I.; Bernal-Agustin, J. Genetic algorithms applied to the design of large power distribution systems. IEEE Trans. Power Syst. 1998, 13, 696–703. [Google Scholar] [CrossRef]
- Scheidler, A.; Thurner, L.; Braun, M. Heuristic optimisation for automated distribution system planning in network integration studies. IET Renew. Power Gener. 2018, 12, 530–538. [Google Scholar] [CrossRef]
- Celli, G.; Pilo, F.; Pisano, G.; Soma, G. Optimal Planning of Active Networks. In Proceedings of the 16th Power Systems Computation Conference (PSCC), Glasgow, UK, 14–18 July 2008; Curran: Red Hook, NY, USA, 2008; ISBN 9781617388576. [Google Scholar]
- Jordehi, A.R. Optimisation of electric distribution systems: A review. Renew. Sustain. Energy Rev. 2015, 51, 1088–1100. [Google Scholar] [CrossRef]
- Wruk, J.; Cibis, K.; Zdrallek, M.; Landsverk, H. Automated planning of smart low voltage networks using an evolutionary algorithm. In Proceedings of the 25th International Conference on Electricity Distribution (CIRED), Madrid, Spain, 3–6 June 2019. [Google Scholar]
- Fernandez, L.P.; Roman, T.G.S.; Cossent, R.; Domingo, C.M.; Frias, P. Assessment of the Impact of Plug-in Electric Vehicles on Distribution Networks. IEEE Trans. Power Syst. 2011, 26, 206–213. [Google Scholar] [CrossRef]
- Stetz, T.; Wolf, H.; Probst, A.; Eilenberger, E.; Drenan, Y.-M.S.; Kämpf, E.; Schöllhorn, D.; Schmidt, S. Stochastic Analysis of Smart-Meter Measurement Data. In Proceedings of the VDE-Kongress, Stuttgart, Germany, 5–6 November 2012. [Google Scholar]
- Stetz, T. Autonomous Voltage Control Strategies in Distribution Grids with Photovoltaic Systems: Technical and Economic Assessment. Master’s Thesis, University of Kassel, Kassel, Germany, 2014. [Google Scholar]
- Georgilakis, P.S.; Hatziargyriou, N.D. A review of power distribution planning in the modern power systems era: Models, methods and future research. Electr. Power Syst. Res. 2015, 121, 89–100. [Google Scholar] [CrossRef]
- Norwegian Statistics Bureau. Energy Consumption in Households. Available online: https://www.ssb.no/en/energi-og-industri/statistikker/husenergi/hvert-3-aar (accessed on 15 January 2020).
- Norwegian Electric Vehicle Association. Norwegian EV Owners Survey. 2017. Available online: https://elbil.no/ (accessed on 15 January 2020).
- Degefa, M.Z.; Sæle, H.; Andresen, C. Analysis of Future Loading Scenarios in a Norwegian LV Network. In Proceedings of the International Conference on Smart Energy Systems and Technologies (SEST), Porto, Portugal, 9–11 September 2019; IEEE: Piscataway, NJ, USA, 2019; ISBN 978-1-7281-1156-8. [Google Scholar]
- Norwegian Statistics Bureau. Statistics Norway. Available online: https://www.ssb.no/ (accessed on 15 January 2020).
- Navigant; Kompetenzzentrum Elektromobilität; RE-xpertise. Verteilnetzausbau für die Energiewende, Commissioned by Agora Verkehrswende, Agora Energiewende and The Regulatory Assistance Project (RAP). 2019. Available online: https://static.agora-energiewende.de/fileadmin2/Projekte/2018/Netzausbau_Elektromobilitaet/Agora-Verkehrswende_Agora-Energiewende_EV-Grid_WEB.pdf (accessed on 15 January 2020).
- Olivella-Rosell, P.; Villafafila-Robles, R.; Sumper, A.; Bergas-Jané, J. Probabilistic Agent-Based Model of Electric Vehicle Charging Demand to Analyse the Impact on Distribution Networks. Energies 2015, 8, 4160–4187. [Google Scholar] [CrossRef]
- Entsog; Entso-E. TYNDP 2018 Scenario Report. Main Report; Brussels. 2018. Available online: https://www.entsog.eu/sites/default/files/files-old-website/publications/TYNDP/2018/entsos_tyndp_2018_Final_Scenario_Report.pdf (accessed on 15 January 2020).
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid. IEEE Trans. Power Syst. 2009, 25, 371–380. [Google Scholar] [CrossRef]
- Stoeckl, G.; Witzmann, R.; Eckstein, J. Analyzing the capacity of low voltage grids for electric vehicles. In Proceedings of the IEEE Electrical Power and Energy Conference (EPEC), Winnipeg, MB, Canada, 3–5 October 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 415–420. ISBN 978-1-4577-0405-5. [Google Scholar]
- Probst, A.C.; Braun, M.; Backes, J.; Tenbohlen, S. Probabilistic analysis of voltage bands stressed by electric mobility. In Proceedings of the 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies (ISGT Europe), Manchester, UK, 5–12 December 2011; IEEE: Piscataway, NJ, USA, 2011; ISBN 978-1-4577-1421-4. [Google Scholar]
- Cross, J.D.; Hartshorn, R. My Electric Avenue: Integrating Electric Vehicles into the Electrical Net-works. In Proceedings of the 6th Hybrid and Electric Vehicles Conference (HEVC 2016), London, UK, 2–3 November 2016; Curran Associates Inc.: Red Hook, NY, USA, 2017; ISBN 978-1-78561-294-7. [Google Scholar]
- Papadopoulos, P.; Skarvelis-Kazakos, S.; Grau, I.; Cipcigan, L.; Jenkins, N. Electric vehicles’ impact on British distribution networks. IET Electr. Syst. Transp. 2012, 2, 91. [Google Scholar] [CrossRef]





| Classification | Trafo Capacity in kVA | Number of Customers | Line Length in km | PL in kW |
|---|---|---|---|---|
| Rural | 200 | 27 | 3.4 | 5.86 |
| Urban 1 | 315 | 12 | 0.75 | 7.8 |
| Urban 2 | 500 | 87 | 0.89 | 3.7 |
| Network | Scenario | PL in kW |
|---|---|---|
| Rural 1 | BE2020 | 6.7 |
| DG2040 | 7.0 | |
| Urban1 | BE2020 | 10.0 |
| DG2040 | 10.5 | |
| Urban 2 | BE2020 | 3.8 |
| DG2040 | 4.3 |
| Networks/Scenarios | Traditional | Novel |
|---|---|---|
| Rural BE2020 | 18.032 € | 3.693 € |
| Network | Scenario | Variant | PL in kW |
|---|---|---|---|
| Rural 1 | DG2040 | Pch = 11 kW | 8.5 |
| Urban 1 | DG2040 | Pch = 11 kW | 11.0 |
| Urban 2 | DG2040 | Pch = 11 kW | 5.5 |
| Scenario | Constraint | Optimal Measure |
|---|---|---|
| Urban 1, 100% EV at 11 kW | Undervoltage |
|
| Urban 2, 100% EV at 11 kW | Thermal |
|
| Networks/Scenarios | Traditional | Novel |
|---|---|---|
| Rural DG2040 11 kW | 41.438 € | 4.128 € |
| Urban 1 DG2040 11 kW | 2.084 € | 2.084 € |
| Urban 2 DG2040 11 kW | 533 € | 533 € |
| Network | Variant | EVs per HH |
|---|---|---|
| Urban 1 | Status quo mix | 1.8 |
| Urban 1 | 11 kW charging | 0.8 |
| Urban 2 | Status quo mix | 0.4 |
| Urban 2 | 11 kW charging | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wruk, J.; Cibis, K.; Resch, M.; Sæle, H.; Zdrallek, M. Optimized Strategic Planning of Future Norwegian Low-Voltage Networks with a Genetic Algorithm Applying Empirical Electric Vehicle Charging Data. Electricity 2021, 2, 91-109. https://doi.org/10.3390/electricity2010006
Wruk J, Cibis K, Resch M, Sæle H, Zdrallek M. Optimized Strategic Planning of Future Norwegian Low-Voltage Networks with a Genetic Algorithm Applying Empirical Electric Vehicle Charging Data. Electricity. 2021; 2(1):91-109. https://doi.org/10.3390/electricity2010006
Chicago/Turabian StyleWruk, Julian, Kevin Cibis, Matthias Resch, Hanne Sæle, and Markus Zdrallek. 2021. "Optimized Strategic Planning of Future Norwegian Low-Voltage Networks with a Genetic Algorithm Applying Empirical Electric Vehicle Charging Data" Electricity 2, no. 1: 91-109. https://doi.org/10.3390/electricity2010006
APA StyleWruk, J., Cibis, K., Resch, M., Sæle, H., & Zdrallek, M. (2021). Optimized Strategic Planning of Future Norwegian Low-Voltage Networks with a Genetic Algorithm Applying Empirical Electric Vehicle Charging Data. Electricity, 2(1), 91-109. https://doi.org/10.3390/electricity2010006






