Prediction and Analysis of Nuclear Explosion Radioactive Pollutant Diffusion Model

Abstract

This study presents a model for the dispersion of radioactive smoke clouds from a nuclear weapon explosion. A model based on a modified Settlement model is chosen to simulate the dispersion of radioactive contaminants from a nuclear explosion in the atmosphere. The arrival time and dose rate of radioactive fallout at various distances in the downwind direction are given for different equivalents of the surface explosion and typical meteorological conditions. Thus, the prediction of the dispersion of radioactive contaminants from a nuclear explosion can be achieved under the conditions of known nuclear explosion equivalence and local meteorological parameters. This provides a theoretical basis for the estimation of the affected environment and the input of rescue forces after the explosion.

1. Introduction

Nuclear weapons are the most powerful type ever manufactured and possessed by mankind. The world’s current stockpile of nuclear weapons is sufficient to destroy the entire planet [1,2]. On 22 January 2021, the United Nations Treaty on the Prohibition of Nuclear Weapons (TPNW) was enforced, making the development, possession, and use of nuclear weapons illegal [3]. Despite relentless global efforts to prevent the proliferation of nuclear weapons [4,5], as nuclear technology continues to advance, the trend is becoming pronounced toward nuclear confrontation and proliferation at the regional level, and the activation of nuclear terrorism is exposing national security to new threats. If a nuclear war were to break out, it would cause global climate change [6] and unrecoverable disturbances to the marine environment [7], thus affecting agriculture, fisheries, and animal husbandry, and ultimately causing a globalized food problem [8,9] with devastating consequences for the world. In a future war, if nuclear weapons are used in a military conflict, no human beings would be spared worldwide.

In addition to the hot fireballs and shockwave damage that results directly from the detonation of a nuclear weapon, it can also be a serious hazard, i.e., the spread of the radioactive smoke cloud from a nuclear explosion. The dispersal of radioactive contaminants from nuclear explosions refers to the transport of radioactive ¹³⁷Cs, ¹³¹I, ⁹⁰Sr, and other particles [10,11,12] over time and space, contaminating the ground, water, air, and various objects [13]. This process can last for months, years, or even longer, starting at the moment of the explosion [10,12,14]. Before the first nuclear tests were conducted, scientists had already predicted that such tests would cause radioactive contamination [15]. Many nuclear weapons tests throughout history have resulted in severe radioactive contamination of indigenous peoples in the vicinity of the test sites, and the alarming rates of thyroid and other cancers have increased the importance of research into radioactive fallout [16,17,18,19].

The radioactive smoke cloud produced by a nuclear explosion carries most of the remaining radioactive products after nuclear fission or nuclear fusion, and its drifting under the action of the atmosphere causes serious ground-level radioactive contamination. This phenomenon is crucial to study the movement and dispersion law of the radioactive smoke cloud of a nuclear explosion in the atmospheric environment. The atmospheric transport processes of radionuclides are affected by weather and meteorological conditions, such that general radiological dispersion models need to consider the driving factors of the meteorological field [20,21]. Leelössy et al. [22] provided a comprehensive review of models for radionuclide dispersion with respect to physical mechanisms, numerical methods, and practical applications. The mainstream atmospheric dispersion algorithms for radionuclides are often based on Gaussian plume models [23,24,25]. Liu et al. [26] improved the Gaussian plume model using ground reflection coefficients and corrected heights to predict the pollutant leak points and concentrations using an inverse calculation method.

For radioactive dispersion in nuclear explosions, the Gaussian plume model is not applicable due to the discontinuity of the source phase, and new computational models have been developed [27]. The earliest WSEG models [28] were based on the “smearing” of smoke clouds, which is equivalent to a cloud of smoke dragging across the ground, causing ground subsidence. Because of its simplicity and ease of application, the WSEG model has been widely used in damage assessment studies for several years. Subsequently, its prediction accuracy has been improved [29,30]. The DNAF-1 model, based on WSEG, is suitable for subsidence simulations of small-yield nuclear explosions and has better accuracy than WSEG [31].

The Defense Land Fallout Interpretative Code (DELFIC) model [32,33] is the standard type for subsidence forecasting in the USA. It describes the entire particle formation and subsidence process in terms of physical principles and takes into account the various factors that influence particle transport. However, this model is very complex because of several factors. Therefore, simplified models have been developed: the SEER model [34], the SEER II model [35], the Hotspot model [36], and the SIMFIC model [37]. The characteristics of these models are that the radioactive smoke cloud of a nuclear explosion is a rising bubble and the height of the smoke cloud is approximately proportional to the square root of the rise time, which is crucial to establishing the vertical trajectory of the particles, while its horizontal movement depends entirely on the wind field.

In order to predict the concentration distribution of radioactive contaminants in the atmosphere from a nuclear explosion in real time, we improved the Settlement model based on MATLAB, using time segmentation processing and coordinate conversion methods such that it can calculate the dispersion of the radioactive contaminants from a nuclear explosion and the change in wind direction. Thus, the application scenario is in line with the real situation of the dispersion of radioactive contaminants from a nuclear explosion. The model can predict changes in the radiation area on the ground from the nuclear explosion and meteorological parameters, and alert personnel downwind, directing them to evacuate the danger zone or take appropriate protection and concealment, thereby reducing the damage caused by the radioactive fallout from the nuclear explosion.

2. Mathematical Principles of Diffusion Models

In order to obtain accurate and rapid simulation calculation results, different mathematical models should be established for different cases of pollutant dispersion in the atmosphere [22]. After a nuclear explosion occurs, a large number of radionuclides are released. The common diffusion models for the diffusion of hazardous, radioactive substances are the Lagrange model, Gaussian model, and Settlement model. The Lagrange model is a set of first-order stochastic modes describing the motion of many particles. It is a widely used and mature model for radionuclide dispersion simulation, especially in the Fukushima nuclear accident in Japan [38,39,40,41]. The model focuses on the simulation of radionuclide dispersion trajectories. The Gaussian model is based on a non-random variation of the plume with wind speed in the x-direction, a Gaussian distribution in the y-direction, and vertical z-direction at a steady state [42,43,44,45]. The Settlement model is theoretically simple and fast and can provide rapid simulation results in nuclear emergency situations, but it is based on the simplification of the ideal situation, such that the accuracy of the calculation results is slightly inferior compared to other models [44].

2.1. Basic Parameters of the Diffusion Model

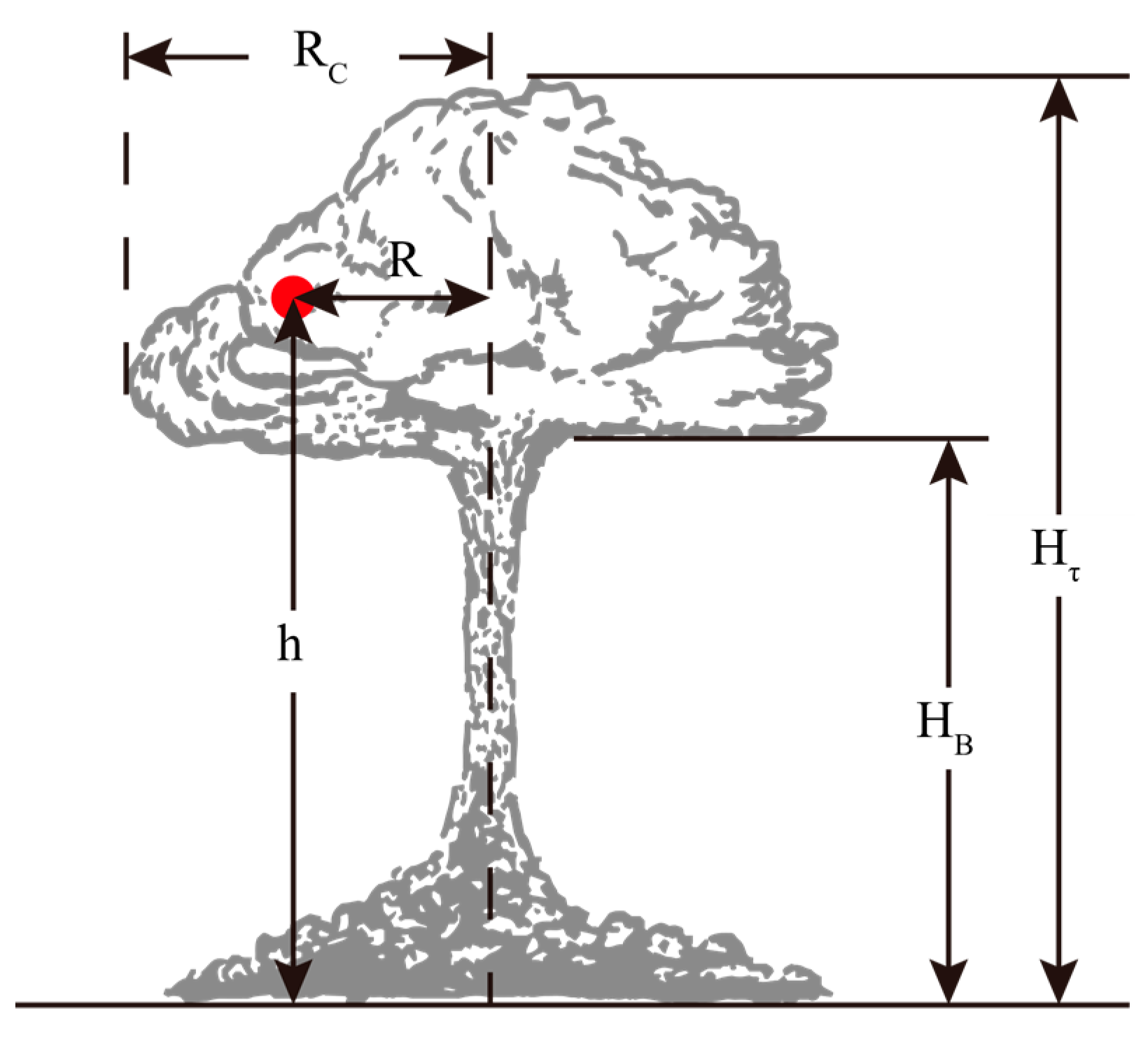
2.1.1. Stable Cloud Geometry Data

After detonation, the body of the nuclear bomb releases enormous energy due to atomic fission or fusion reactions, the temperature in the nuclear reaction area rises to tens of thousands of degrees Celsius, and the pressure rises to tens of billions of atmospheres. Under such high temperatures and pressure, the projectile instantly vaporizes into a plasma gas cloud [46], heating and pressurizing the surrounding cold air. In addition, the high temperature and pressure of the gas mass with rapid outward expansion will form a huge fireball that exists for a short period. When the nuclear explosion produced by the fireball is extinguished, it rises and expands rapidly, forms a “mushroom” smoke cloud (Figure 1), and an intense vortex motion is generated inside the smoke cloud [47,48,49]. The strong suction and coiling effect trap the ground dust and other materials in the smoke cloud [50,51]. When the smoke cloud reaches its maximum height, the temperature and pressure inside the cloud are similar to those of the surrounding atmosphere, the vortex motion has disappeared, and the upward motion of the cloud has stopped, thus entering the turbulent separation phase [52], which is called “Stable Cloud”.

The height of the cloud cap $H_B$ and the height of the top $H_{\tau }$ in the geometry of the stable radioactive smoke cloud can be expressed as follows:

$$\begin{array}{c}{H}_B=a{W}^b\\ H_{\tau }=c{W}^d\end{array}$$

(1)

Among them, $W$ represents the nuclear explosion energy equivalent (kt), the unit of $H_B$ and $H_{\tau }$ is meters, and the parameters are as follows:

$$\begin{array}{l}a=2228, b=0.3463; W\le 4.07\\ a=2661, b=0.2198; W>4.07\\ c=3597, d=0.2553; W<2.29\\ c=3170, d=0.4077; 2.29\le W<19\\ c=6474, d=0.1650; W\ge 19\end{array}$$

The radius fitting formula of the stable cloud cap is:

$$R_C=exp\left[6.7553+0.32055lg\left(W\right)+0.01137478{(lg\left(W\right))}^2\right]$$

(2)

where $W$ denotes the nuclear explosion energy equivalent (kt).

2.1.2. Scale Distribution and Activity Distribution of Radioactive Particles

The size distribution of radioactive particles produced during a nuclear explosion is very large, ranging from sub-micron to millimeter scale, and their settling velocity varies considerably, necessitating scale gradation calculations. Typically, the particle scale distribution is log-normal. As different radioactive particles are produced at various time points, the activity varies at different particle scales, according to Bridgman’s method, i.e., the particle activity scale distribution is a weighted average of the activity surface distribution and the bulk distribution. The log-normal distribution function has many advantages and is chosen as the scale distribution function in the model.

$$N\left(D\right)dD=\frac{1}{\sqrt{2\pi }\overline{D}lnS}exp[-\frac{{\left(lnD-ln\overline{D}\right)}^2}{2lnS}]$$

(3)

where: $D$ is the particle diameter; $N\left(D\right)dD$ indicates the number of particles scaled between $D$ and $D+dD$ as a percentage of the total; $\overline{D}$ is the geometric mean particle diameter; $S$ is the geometric standard deviation.

The different sizes of radioactive particles in nuclear smoke have varied activity levels, which could be attributed to the different processes and ways in which radioactive particles are formed in the smoke cloud. In the early stages of the nuclear explosion, the high temperatures generated by the bomb cause the bomb body and its surrounding material to vaporize completely and then condense into radioactive particles. This particulate radioactivity is uniformly distributed in a bulk distribution, which has a low particle scale, in addition to a large amount of environmental material, such as soil, which is trapped in it as the nuclear smoke cloud rises [46]. The melted and vaporized radioactive material condenses as it cools and adheres to the surface of these environmental materials, resulting in a surface distribution of these particles, which has a large particle scale.

Due to the different conditions of the explosion, the impact of particle activity distribution is related to factors such as the equivalent burst height and burst area soil composition. Typically, the higher the burst formation of particles, the smaller the geometric mean diameter, the greater the possibility of a radioactive body distribution, and the greater the possibility of forming a radioactive surface distribution. Therefore, due to the air explosion, most of the radioactive material is in the air for a prolonged period, while in the ground explosion, most of the radioactive material quickly settles to the ground.

In this study, Bridgman’s methods are used [30], i.e., the activity-scaled distribution of a particle is a weighted average of the activity surface and body distributions, such that the number-scaled distribution of a particle is log-normal. Thus, it can be seen that the surface and body distributions of the particle activity are log-normal, except that the corresponding geometric mean diameters become $\left(ln\overline{D}+2l{n}^{2}S\right)$ and $\left(ln\overline{D}+3l{n}^{2}S\right)$, respectively, and the geometric standard deviation is $S$. Next, we have:

$$A\left(D\right)dD=C_{1}As\left(D\right)dD+C_{2}Av\left(D\right)dD$$

(4)

where $A\left(D\right)dD$ represents the activity in the interval from diameter $D$ to $D+dD$ as a percentage of the total activity of all particles, and $As\left(D\right)$ and $Av\left(D\right)$ are the surface and bulk distributions of particle activity, respectively: $C_1=0.32$, $C_2=0.68$.

In order to simplify the calculation, the particle scale is divided into several intervals, and the percentage of the total activity in any particle size interval can be obtained by integrating the particle size: activity expression for the particle size in the interval $\left[D_i,D_{i+1}\right]$, and the share of the total activity of the radioactive particles $F\left(i\right)$ satisfies:

$$F\left(i\right)={{\displaystyle \int }}_{D_i}^{D_{i+1}}A\left(D\right)dD$$

(5)

In this study, equal mass grading was used, i.e., the mass of particles in each subclass is identical. The percentage of total radioactivity and gravitational settling velocity calculated for the median particle radius of the 20 particle size intervals of the ground burst are listed in

Table 1. Percentage of total radioactivity and gravitational settling velocity in the radius of the median particle of the ground burst.

Median Particle Radius/μm	Radioactivity Percentage Fi/%	Vg/(m/s)	Median Particle Radius/μm	Radioactivity Percentage Fi/%	Vg/(m/s)
4.3	9.35	0.006	70.8	3.95	0.915
8.6	7.99	0.023	84.4	3.87	1.444
13	6.44	0.053	101	3.8	1.427
17.7	5.65	0.096	122	3.73	1.78
22.7	5.15	0.153	149	3.68	2.228
28.3	4.8	0.224	185.7	3.62	2.816
34.6	4.55	0.306	238.7	3.58	3.622
41.7	5.35	0.391	323.8	3.53	4.812

.

2.1.3. Scale Distribution and Activity Distribution of Radioactive Particles

The horizontal transport and dispersion of radioactive particles is based on the Monte Carlo model of smoke clouds; its dispersion is based on Gifford’s theory of relative tropospheric dispersion, which is characterized by the stochastic nature of atmospheric motion and the transient nature of explosive smoke cloud generation. The motion of the smoke center could be computed as described previously in the following equation:

$$\{\begin{array}{c}{x}_{n+1}=x_n+u_{n+1}\Delta t\\ y_{n+1}=y_n+v_{n+1}\Delta t\end{array}$$

(6)

Among these, $\left(x_{n+1},y_{n+1}\right)$ is the central position of the puff at time $t+\Delta t$, $\left(x_n,y_n\right)$ is the position at time and t, and $\left(u_{n+1},v_{n+1}\right)$ is the wind speed at time $t+\Delta t$, calculated by the following formula:

$$\{\begin{array}{c}{u}_{n+1}=u_{n}R\left(\Delta t\right)+{\sigma }_u{\left(1-R^2\left(\Delta t\right)\right)}^{1/2}\\ v_{n+1}=v_{n}R\left(\Delta t\right)+{\sigma }_v{\left(1-R^2\left(\Delta t\right)\right)}^{1/2}\end{array}$$

(7)

Among them, $\left(u_n,v_n\right)$ is the wind speed at time $t$, $R\left(\Delta t\right)$ is the correlation coefficient, and $\left({\sigma }_u,{\sigma }_v\right)$ is the turbulent velocity variance. Currently, there is no regular model result of the turbulent velocity variance in the troposphere, and the assumption that the degree of turbulence is not too large can be used, i.e., ${\sigma }_{u,v}~{\overline{u}}_{x,y}/10$, where ${\overline{u}}_{x,y}$ is the average wind speed of the layer where the smoke cloud is located. The correlation coefficient is in exponential form, i.e., $R\left(\Delta t\right)=e^{-\Delta t/t_L}$, where $t_L$ is the Lagrangian time scale of tropospheric turbulence.

Typically, atmospheric nuclear explosions and radioactive fallout occur in the troposphere, where the tropospheric atmosphere inevitably contributes to nuclear smoke clouds with the passage of time. However, the laws of tropospheric atmospheric dispersion have not been well theorized, especially for contrail dispersion. Gifford et al. [53] proposed a formula for the variance of the horizontal diffusion of puffs under uniform turbulent conditions via random force theory:

$${\sigma }_y^2={\sigma }_0^2+2K{t}_L\left[\frac{t}{t_L}-\left(1-e^{-\frac{t}{t_L}}\right)-\frac{c}{2}{\left(1-e^{-\frac{t}{t_L}}\right)}^2\right]$$

(8)

where ${\sigma }_0$ is the variance of the initial time of the smoke cloud, which is assumed to be $R/4.3$, $K$ is the vortex diffusion coefficient, and $t_L$ is the Lagrangian time scale of large-scale atmospheric motion. $c$ is related to the characteristics of the original source, obtained by comparing the results of the similarity theory using the following formula by Gifford et al. [53]:

$$c\approx 1-{\sigma }_0^{\frac{2}{3}}/{\left(2K{t}_L\right)}^{1/3}$$

(9)

Since the diffusion coefficient $K$ and the Lagrange time scale are difficult to determine, statistical methods were applied, and $K$ could be roughly estimated by the following formula:

$$K=1.43\times {10}^4{e}^{0.144Z_c}$$

(10)

2.2. Sedimentation Rate Diffusion Factor

2.2.1. Sedimentation Rate Function

The settling rate fitting nuclear explosion radioactive smoke cloud dispersion calculation model is based on the settling rate function, considering lateral, vertical, and turbulent dispersion effects, calculating the accumulation of radioactive settling in time, and then fitting the ground radiation dose by equivalent dose rate. The sedimentation rate function selected for this model is as follows:

$$g\left(t\right)=\frac{4sin\left[\pi \left(3-\alpha \right)/2\right]}{\pi T\left(3-\alpha \right)}\frac{{\left(\frac{T}{t}\right)}^{\alpha }}{{\left[1+{\left(\frac{T}{t}\right)}^2\right]}^2}$$

(11)

where, g(t) is the unit activity sedimentation rate function (s⁻¹), $t$ is the time (s), and $\alpha$ is a dimensionless parameter:

$$\begin{array}{l}\alpha =1.06; {10}^{-3}\le W\le {10}^{-1}\\ \alpha =1.0875+0.0119431lnW; {10}^{-1}<W<{10}^3\\ \alpha =1.17; W\ge {10}^3\end{array}$$

$T$ is the time scale (s) that can pass through the maximum time point of $g\left(t\right)$:

$$t_{max}=T\sqrt{\frac{4-\alpha }{\alpha }}$$

(12)

$$\begin{array}{l}{t}_{max}=30W^{0.41556}; {10}^{-3}\le W\le 1kt\\ t_{max}=30W^{0.65407}; 1<W\le {10}^3\\ t_{max}=893.616W^{0.16273}; {10}^3<W\le {10}^4\\ t_{max}=2497.18W^{0.05115}; {10}^4<W\le {10}^5\end{array}$$

2.2.2. Far-Field Correction

The above settling rate function fits the simulated data in the near field or early stages of settling of the radioactive smoke cloud; however, there is a large gap in the far field, such that a far-field correction has to be added.

$$F\left(t\right)=exp\left\{-\left[ln\left(\frac{g\left(t\right)}{k}\right)+{\left(\frac{t}{T_2}\right)}^2\right]\left[1-exp\left(\frac{t}{a{t}_c}\right)\right]\right\}$$

(13)

where: $a=1.443$; $k=9.867\times {10}^{-5}{w}^{-0.26945}\left(s^{-1}\right)$; $T_2=8160W^{0.2406}\left(s\right)$; and

$$\begin{array}{l}{t}_c=14667W^{0.26208}\left(s\right); W\le 98.787kt\\ t_c=exp\left[\begin{array}{c}10.124706+0.1861768lnw\\ -0.008660444{(lnW)}^2\end{array}\right]\left(s\right); W>98.787kt\end{array}$$

2.2.3. Vertical Diffusion

The settling velocity of the particles of nominal particle size at different heights can be expressed as:

$$f\left(z\right)=f_0{e}^{\varsigma z}$$

(14)

where $f_0=1.6538 \left(\mathrm{m}/\mathrm{s}\right)$ and $\varsigma =2.9\times {10}^{-5} \left({\mathrm{m}}^{-1}\right)$. Then, the time for the particle to reach the ground is:

$$t_B=-{{\displaystyle \int }}_{z_B}^{0}dz/f\left(z\right)=\frac{1-exp\left(-\varsigma z_B\right)}{\varsigma f_0}$$

(15)

To make it easier to give the longitudinal diffusion parameters of a nuclear explosion, first define a diffusion parameter related to the explosion yield ${\sigma }_W$:

$$\begin{array}{ll}& {\sigma }_W=R_i;W\le 10kt\\ & {\sigma }_W=R_i\left(1+3lo{g}_{10}W\right)/4;10<W<1000\\ & {\sigma }_W=2.5R_i;W\ge 1000\end{array}$$

Then, the longitudinal diffusion parameters at different times and downwind positions are:

$$\begin{array}{ll}& {\sigma }_c={\sigma }_{\sigma };t\le t_0\\ & {\sigma }_c={\sigma }_W+\frac{t-t_0}{t_B-t_0}\left(\frac{R_s}{2}-{\sigma }_W\right);t_0<t<t_B\\ & {\sigma }_c=\frac{R_s}{2};t\ge t_B\end{array}$$

2.2.4. Turbulent Diffusion Correction

Considering the correction for longitudinal diffusion by atmospheric turbulence, the result is:

$$\begin{array}{l}{\sigma }^2={\left({\sigma }_c^{\frac{2}{3}}+\frac{2}{3}{\left(\xi \right)}^{\frac{1}{3}}t\right)}^3; t\le t_1\\ {\sigma }^2={10}^6{\left(3{\sigma }_c^{\frac{2}{3}}+2{\left(\xi \right)}^{\frac{1}{3}}t-2000\right)}^3; t>t_1\end{array}$$

(16)

where $\frac{2}{3}{\left(\xi \right)}^{\frac{1}{3}}=0.016522W^{-0.10233}$ and $t_1=\frac{1000-{\sigma }_c^{\frac{2}{3}}}{\frac{2}{3}{\left(\xi \right)}^{\frac{1}{3}}}$.

2.2.5. Lateral Diffusion Parameters

The lateral diffusion is mainly due to the influence of wind shear and its diffusion parameters can be expressed as follows:

$${\sigma }_s^2={\left[\frac{S_y\left(z_T-z_B\right)t}{10}\right]}^2$$

(17)

where $S_y$ denotes the approximate vertical wind shear (m/s). Thus, the equation is as follows:

$${\sigma }_y^2={\sigma }^2+{\sigma }_s^2$$

(18)

2.2.6. Sedimentation Rate Diffusion Factor

Based on the parameters provided above, the settling rate diffusion factor at different arrival times and locations can be expressed as follows:

$$gf\left(x,y,t\right)=\frac{g\left(t\right)}{\sqrt{2\pi }\pi \sigma {\sigma }_y[1+{\left(\frac{x-Vt}{\sigma }\right)}^2}exp\left[-\frac{1}{2}{\left(\frac{y}{{\sigma }_y}\right)}^2\right]$$

(19)

$V$ is the equivalent wind speed (m/s). For the upwind direction, a correction is required, multiplied by the wind correction factor $F_{up}$ above.

$$F_{up}=exp\left\{bx\left[1-exp\left(\frac{x}{c_1}\right)\right]\right\};x<0$$

(20)

If $W\le 10$, $b=0.0176 \mathrm{and} c_1=570$; else if $W>10$, $b=0.08045w^{-0.66}$ and $c_1=-8179.82+3800lnW$. Settling is a cumulative effect in time and this model does not consider resuspension; hence, the settling diffusion factor $xq \left({\mathrm{m}}^{-2}\right)$ is expressed as:

$$xq\left(x,y,t\right)={{\displaystyle \int }}_0^{t}gf\left(x,y,\tau \right)d\tau$$

(21)

3. Programming and Verification

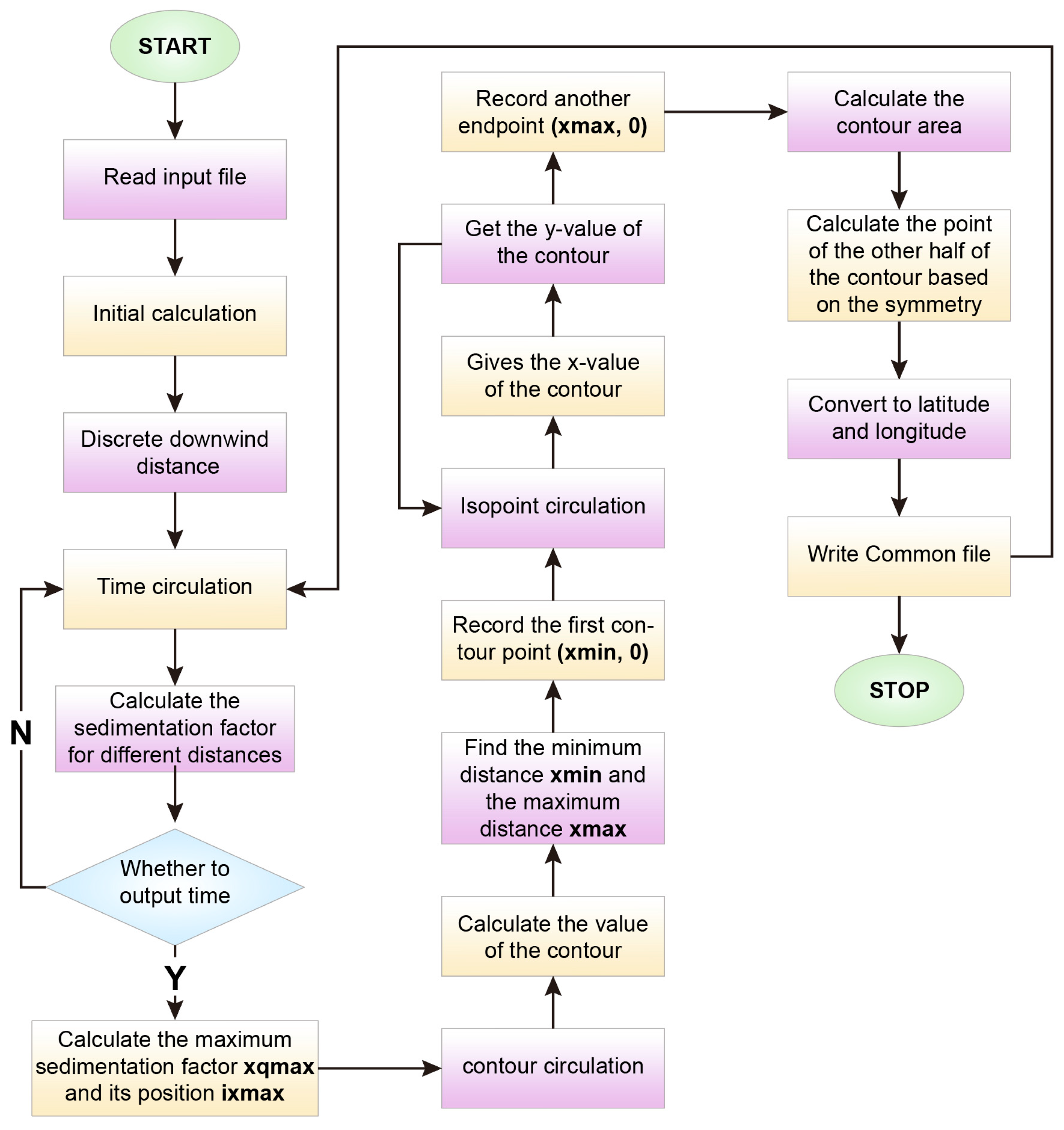
3.1. Programming

The program was written using MATLAB language to simulate the dispersion of radioactive contaminants from a nuclear explosion. Figure 2 shows the flowchart of the program; the input file contains the initial module of a nuclear explosion and the meteorological monitoring module. The initial module of the nuclear explosion includes the explosion equivalent, the coordinates of the burst center, and the exit velocity. The meteorological monitoring module includes the meteorological parameters, such as wind speed, wind direction, and temperature, and transmits them to the simulation calculation module. The simulation calculation module processes the source data, meteorological data, the calculation area size, and other parameters, and substitutes them into the mathematical model for the concentration distribution calculation. The final results of the theoretical numerical prediction of the dose concentration distribution of the radioactive smoke cloud deposition in the atmosphere of the nuclear explosion are obtained.

3.2. Model Verification

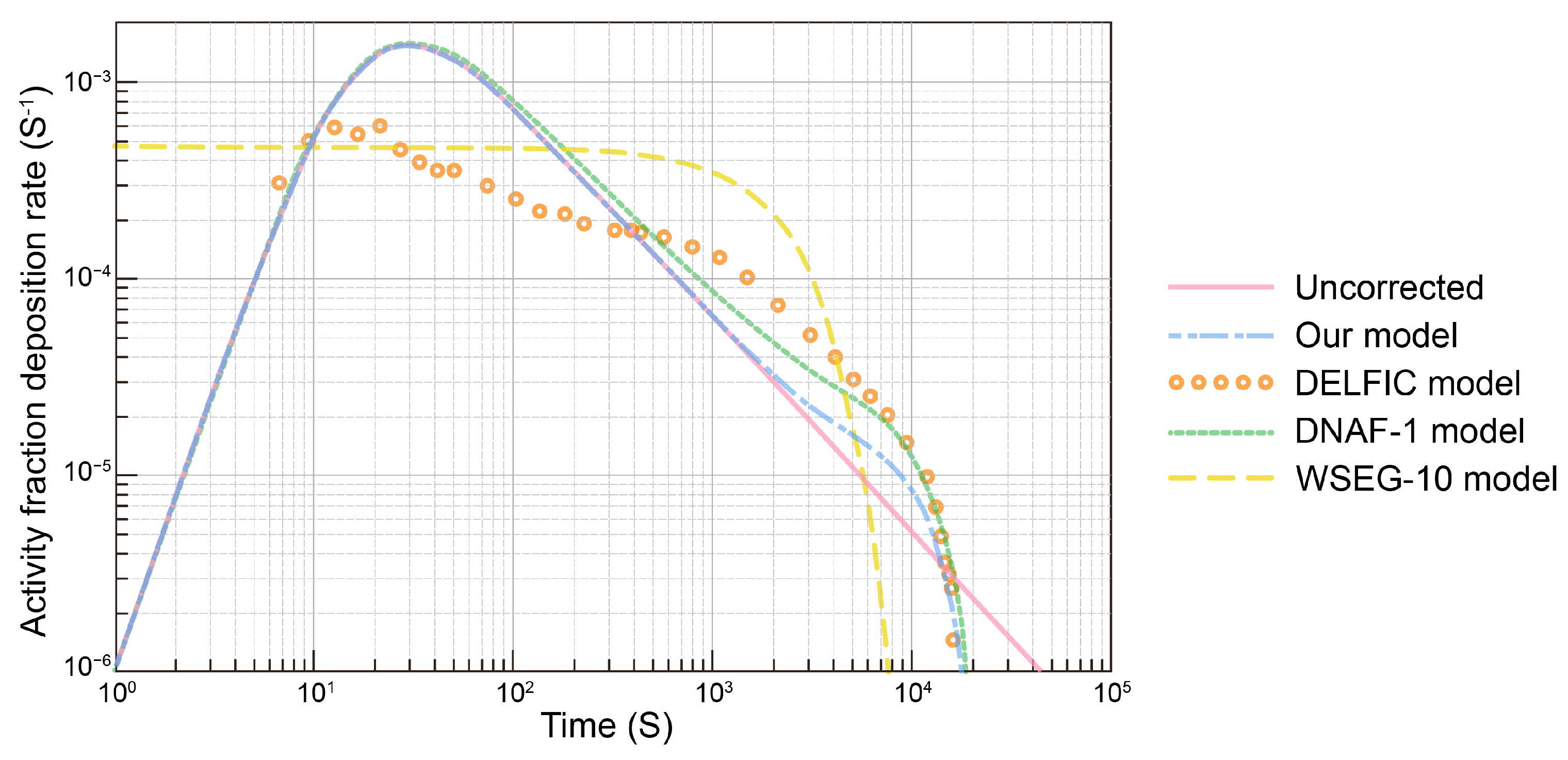
3.2.1. Sedimentation Rate Diffusion Factor Validation

The nuclear explosion radioactive dispersion prediction model DNAF-1 [31] is a computational tool for rapid assessment of the effects of radioactive fallout from a nuclear explosion on the surface based on experimental and simulation data patterns summarized in the USA in the early 1980s [32,33,37]. In order to achieve a rapid and effective evaluation of the nuclear explosion radioactive contaminant dispersion model, compare its accuracy, and verify its practical application. The major computational parameters are referred to for comparison. In the rapid deposition model of the nuclear explosion radioactive smoke cloud, the model for calculating the settling rate dispersion factor is the core of the calculation that determines the whole model algorithm; hence, a direct comparison of its consistency can illustrate the accuracy of the model. Figure 3 shows the distribution of the settling rate diffusion factor with time for the different models at 1 KT explosion equivalent. Compared to the case without adding the far-field approximation correction, each model is calibrated to a specific degree; the comparison reveals that the settling rate diffusion factor of our model is similar to that of the DELFIC model and of the DNAF-1 model with a certain degree of confidence.

3.2.2. Real Historical Data Verification

In this study, the historical nuclear explosion experimental data shown in

Table 2. Information on historical nuclear test data [54,55].

Shot	Time	Height of Burst (m)	Total Yield (kt)	Average Wind Speed (m/s)	Average Wind Direction (°)	Average Wind Shear (s−1)
Sugar	19 November 1951	1.067	1.2	13.1	14.6	0.00311
Koon	7 April 1954	4.145	150	6.2	11.3	0.00133
Zuni	28 May 1956	2.743	3380	4.9	−20.0	0.00225

verified the accuracy of the model. This model was then compared to the DELFIC, DNAF-1, and WSEG-10 models and then with the real observed data. The contour points generated by the model at the same dose were plotted by the visualization software R, as shown in Figure 4. Their heat maps were supplemented with blank values on the grid points using linear interpolation. The data were selected from the three historical nuclear explosions under code names Sugar, Koon, and Zuni, with explosive yields of 1.2, 150, and 3380 kilotons, respectively, to verify the prediction accuracy of the model for large, medium, and small yields.

The inter-model validation and comparison with real recorded observations can be obtained in medium- and small-yield nuclear explosion tests. Our model showed good prediction accuracy, indicating considerable credibility and practical value. However, in large yields, similar to the other three models, our model showed large deviations from the real recorded observations, which might be due to the fact that large-yield nuclear explosions have a high altitude of the radioactive smoke cloud, which spreads over a wide area and is severely affected by the complex meteorological conditions; therefore, all models are less effective in predicting the cloud. Owing to the fact that the Zuni experiment was a nuclear test conducted on Bikini Island, the actual dose detection records were affected by the constraints of the marine environment and the number of ships, mobility, and observation errors, and their observations were not fully accurate isochronous distribution values of the actual dose dispersion; hence, the credibility of the observation data was limited and could only be used as a reference.

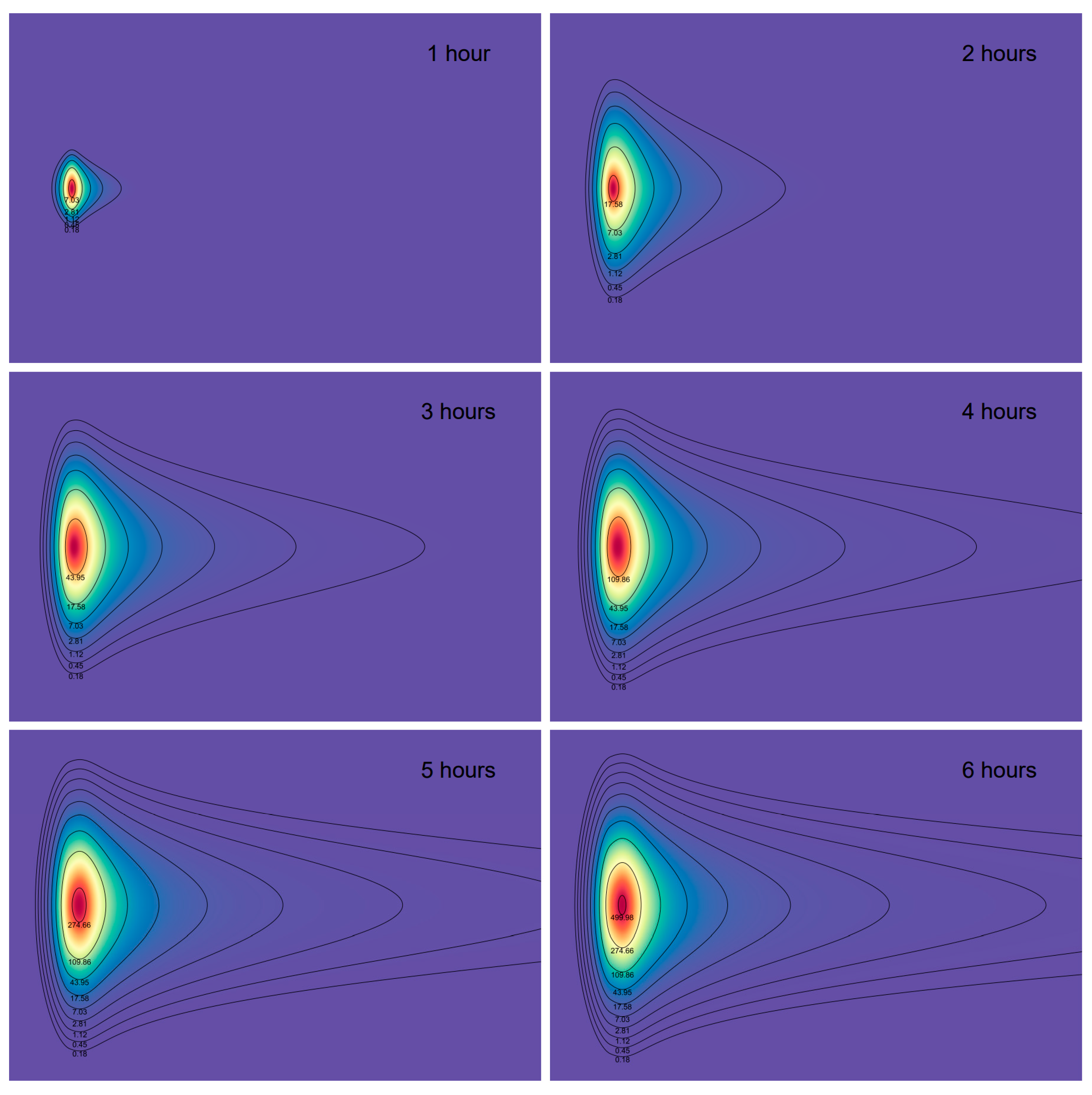
3.2.3. General Validation

Suppose that a nuclear explosion equivalent to 100 kilotons occurs at a certain location and the meteorological conditions of the explosion are an average wind speed of 6 m/s, an average wind direction of 90°, and an average wind shear of 0. The nuclear explosion and meteorological parameters are input into our model, and the predicted contamination dose of radioactive fallout from 1 to 6 h after the explosion is presented by the visualization method described in Figure 5. The radioactive smoke cloud deposition from a nuclear explosion has the following characteristics:

• The maximum radioactive dose and the area of radioactive contamination increase with time in 1–6 h;
• A hot line of radioactive dose extends continuously along the downwind direction;
• The general trend of dose distribution along the direction of the hot line is a gradual decrease with increasing distance;
• The predicted map of radioactive deposition dose varies for each nuclear explosion;
• Radioactive deposition is strongly influenced by the equivalent dose, meteorological conditions, topographic environment, and blast mode.

Therefore, through the above historical data model comparison verification and general verification, it is reasonable to judge that our model as the prediction of nuclear explosion radioactive smoke cloud deposition in terms of time distribution or accuracy has certain reference value and can be used as one of the theoretical bases for nuclear explosion hazard prediction judgment analysis.

4. Conclusions

Nuclear explosion radioactive fallout is the nuclear reaction after the fission or fusion production in the condensation of particles formed in the explosion of the fireball of buoyancy to rise to high altitude [46,49]. Then in the atmosphere under the action of diffusion, settlement to the ground, the formation of a vast area of radioactive contamination. The effect of nuclear explosion radioactive fallout in the nuclear weapons destruction effect is the largest and the duration is the longest [11,12]. Numerical computational models are the most effective tools for simulating radioactive fallout from nuclear explosions, but model accuracy is still an important factor limiting the accuracy of predictions [22]. However, the prediction accuracy of nuclear explosion radioactive smoke cloud deposition is not only related to the diffusion model, but also closely related to the accuracy of the input nuclear explosion equivalent, coupling with the atmospheric diffusion model, etc. In this paper, a hybrid model calculation program for nuclear explosion radioactive smoke cloud deposition with variable wind direction was developed using MATLAB based on the deposition model, which can simulate and calculate the dose distribution of ground-level radioactive deposition with time under the scenario of changing wind conditions. Based on this, the effects of wind speed and atmospheric stability on the dispersion of radioactive contaminants are simulated and analyzed. And through historical data validation, model comparison, and general validation it can be concluded that our model can predict the occurrence range and intensity of radioactive deposition based on the explosion equivalent and the meteorological data at the moment of explosion, and it can be applied to develop the corresponding preventive protection and rescue measures with a certain degree of confidence.

The limitation of this paper is that the subsidence model itself is a simplified model for predicting the dispersion of radioactive smoke clouds, which is fast in calculation but sacrifices some prediction accuracy. In future work, we can try to combine the Gaussian smoke cluster model, the Lagrangian model, or the Eulerian hybrid model for comprehensive testing and comparison, which will hopefully further improve the prediction accuracy of radioactive smoke cloud dispersion of nuclear explosion.