Four-Wave Mixing in Asymmetric Double Quantum Dot Molecule–Metal Nanoparticle Assemblies ^†

Abstract

In this study, the four-wave mixing (FWM) spectrum of a strongly pumped hybrid structure is theoretically examined. The hybrid structure consists of an asymmetric double semiconductor quantum dot (SQD) molecule and a spherical metal nanoparticle (MNP), which are coupled together via long-range Coulomb interaction. Having as a starting point the Hamiltonian of the system, in the dipole and the rotating-wave approximations, we derive a set of nonlinear density matrix equations, which are numerically solved, in the steady-state limit, and then the FWM coefficient is calculated within a range of values of the pump–probe field detuning. The spectral response of the FWM coefficient is investigated, for different values of the pump-field detuning, the electron-tunneling rate, and the energy gap between the upper states in the energy-level scheme of the double SQD molecule, while the interparticle distance between the two components of the structure is modified.

1. Introduction

The coupling between the excitonic and the plasmonic nanoparticles produces collective optical properties, which are quite different from the properties of the individual components, such as emission, dispersion, and absorption. During the last years, these interesting optical effects have attracted scientific interest, both on an experimental and a theoretical level, in hybrid nanostructures that are composed of SQDs and MNPs [1,2,3,4,5]. The study of the Λ-type system that describes the asymmetric double-SQD system has also attracted the scientific interest of several scientists who investigated the pump–probe response and the FWM [6,7], and the Autler–Townes splitting and the tunneling-induced transparency [8,9]. In this work, we are interested in the study of a complex structure in which an asymmetric double-SQD molecule is coupled to an MNP. We start with the Hamiltonian of the system, in the dipole and the rotating-wave approximations, and derive a set of nonlinear density matrix equations, which are numerically solved, in the steady-state limit. Then, the FWM coefficient is calculated within a range of values of the pump–probe field detuning. The spectral response of the FWM coefficient is investigated, for different values of the pump-field detuning, the electron-tunneling rate, and the energy gap between the upper states in the energy-level scheme of the double SQD molecule for different values of the distance between the SQD and MNP.

2. Methods

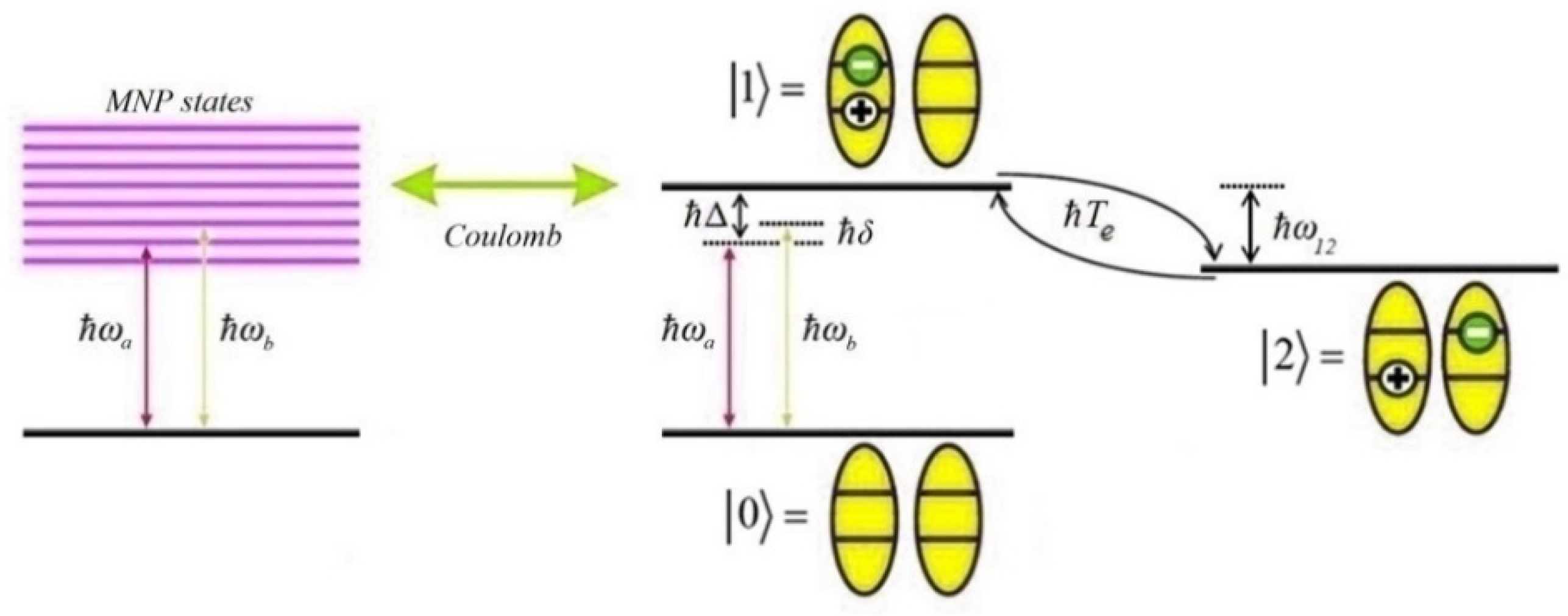
We consider a hybrid molecule consisted of a spherical MNP of radius $a$ and a couple of spherical SQDs of radii $b_{}(<<a)$, in the presence of a polarized external field that is composed of a strong pump field of amplitude $E_a$ and angular frequency ${\omega }_a$ and a weak probe field of amplitude $E_b<<E_a$ and angular frequency ${\omega }_b$. In the energy level configuration presented in Figure 1, the double SQD molecule is modeled as a three-level Λ-type system, while the basic excitations in the MNP are the surface plasmons, which present a continuous spectrum. The incident field excites an electron occupying the ground state $|0\rangle$, thus creating an electron–hole pair that is bound to the same SQD (direct exciton state $|1\rangle$). Due to the transition of this electron to the second SQD, via tunneling, a hole is induced in the first SQD (indirect exciton state $|2\rangle$).

Under the dipole approximation, the Hamiltonian of the hybrid structure is written as $H=H_{SQD}+H_{\mathrm{int}}$, where $H_{SQD}={\displaystyle {\sum }_{n=0,1,2}\left({\mathrm{E}}_n|n\rangle \langle n|\right)}+\hslash T_e\left(|1\rangle \langle 2|+|2\rangle \langle 1|\right)$ is associated to the unperturbed SQD molecule, ${\mathrm{E}}_n$ denoting the energy of state $|n\rangle$, with $n=0,1,2$, where the ground-state energy is set equal to zero $({\mathrm{E}}_0=0)$, $T_e$ symbolizing the tunneling coupling rate and $\mu$ representing the dipole transition matrix element related to the $|0\rangle \leftrightarrow |1\rangle$ transition. The Hamiltonian term $H_{\mathrm{int}}=-\mu (\hslash /\mu ){\displaystyle \sum _{i=1,2}\left\{\left[{\Omega }_i+G_i{\rho }_{10}(t)\right]e^{-i{\omega }_{i}t}+c.c.\right\}}\left(|0\rangle \langle 1|+|1\rangle \langle 0|\right)$ owes its presence to the interaction of the system with the pump and the probe incident fields, where $G_i={\displaystyle \sum _{n=1}^N[s_n{\gamma }_n({\omega }_i)a^{2n+1}{\mu }^2]/(4\pi {\epsilon }_{env}\hslash {\epsilon }_{effS}^2{R}^{2n+4})}$ describes the self-interaction of the SQD, with ${\gamma }_n({\omega }_i)=[{\epsilon }_m({\omega }_i)-{\epsilon }_{env}]/[{\epsilon }_m({\omega }_i)+(n+1){\epsilon }_{env}/n]$, ${\epsilon }_{effS}=(2{\epsilon }_{env}+{\epsilon }_S)/3{\epsilon }_{env}$, where $i=1$ and 2, for the pump field and the probe field contribution, respectively. Here, ${\epsilon }_{env}$, denotes the dielectric constant of the material in which the particles are embedded, ${\epsilon }_S$ is the dielectric constant of the SQD, ${\epsilon }_m(\omega )$ expresses the local uniform dielectric function that characterizes the MNP, and $R$ is the center-to-center distance between the MNP and the SQD. In the expression of $H_{\mathrm{int}}$, the first term ${\Omega }_i=\mu E_i(1+s_a{\gamma }_1{a}^3/R^3)/(2\hslash {\epsilon }_{effS})$ represents the Rabi frequencies of the pump and the probe fields, while the second term expresses the coupling of the double SQD molecule to the MNP-induced field.

Having as a starting point the Hamiltonian, we can show that, under the rotating-wave approximation, the slowly varying density matrix elements obey a set of five differential equations. We proceed to the expansion of the density matrix elements, ${\rho }_{nm}={\rho }_{nm}^{(1)}+{\Omega }_b^{*}{e}^{i\delta t}{\rho }_{nm}^{(2)}+{\Omega }_b{e}^{-i\delta t}{\rho }_{nm}^{(3)}$, according to the first-order Taylor approximation, with respect to ${\Omega }_b$, and derive a set of fifteen differential equations. The FWM coefficient is given by the expression ${\left|{\rho }_{01}^{(3)}\right|}^2$, ${\rho }_{01}^{(3)}$, being calculated numerically, in the steady state.

3. Parameters and Results

In this section, we examine the FWM spectra of a strongly pumped asymmetric tunneling-controlled double SQD–MNP system. The incident field is assumed to have a polarization direction that is parallel to the interparticle axis, and hence, we take $s_a=2$ and $s_n={(n+1)}^2$. The pump-field Rabi frequency is $\hslash {\Omega }_1=3_{}\mathrm{meV}=100\hslash {\Omega }_2$. The radius of the gold nanoparticle is assumed to be equal to ${7.5}_{}\mathrm{meV}$ and its dielectric function is defined according to experimental values presented in ref. [10]. The dielectric constant of the SQD is ${\epsilon }_S=6{\epsilon }_0$, while the dielectric constant of the environment is ${\epsilon }_{env}={\epsilon }_0$. The decay rates of the double SQD molecule are $\hslash {\Gamma }_{10}=0.025\mathrm{meV}$, $\hslash {\Gamma }_{20}=0.000025\mathrm{meV}$ and ${\Gamma }_{12}=0$, while the dephasing rates are $\hslash {\gamma }_{01}=0.22\mathrm{meV}$, $\hslash {\gamma }_{12}=0.1\mathrm{meV}$, $\hslash {\gamma }_{02}=0.001\mathrm{meV}$. The transition $|0\rangle \leftrightarrow |1\rangle$ is characterized by the dipole moment $\mu =0.65\cdot e_{}\mathrm{nm}$, and the corresponding energy gap is $\hslash {\omega }_{01}={\mathrm{E}}_1-{\mathrm{E}}_2={1.4}_{}\mathrm{eV}$.

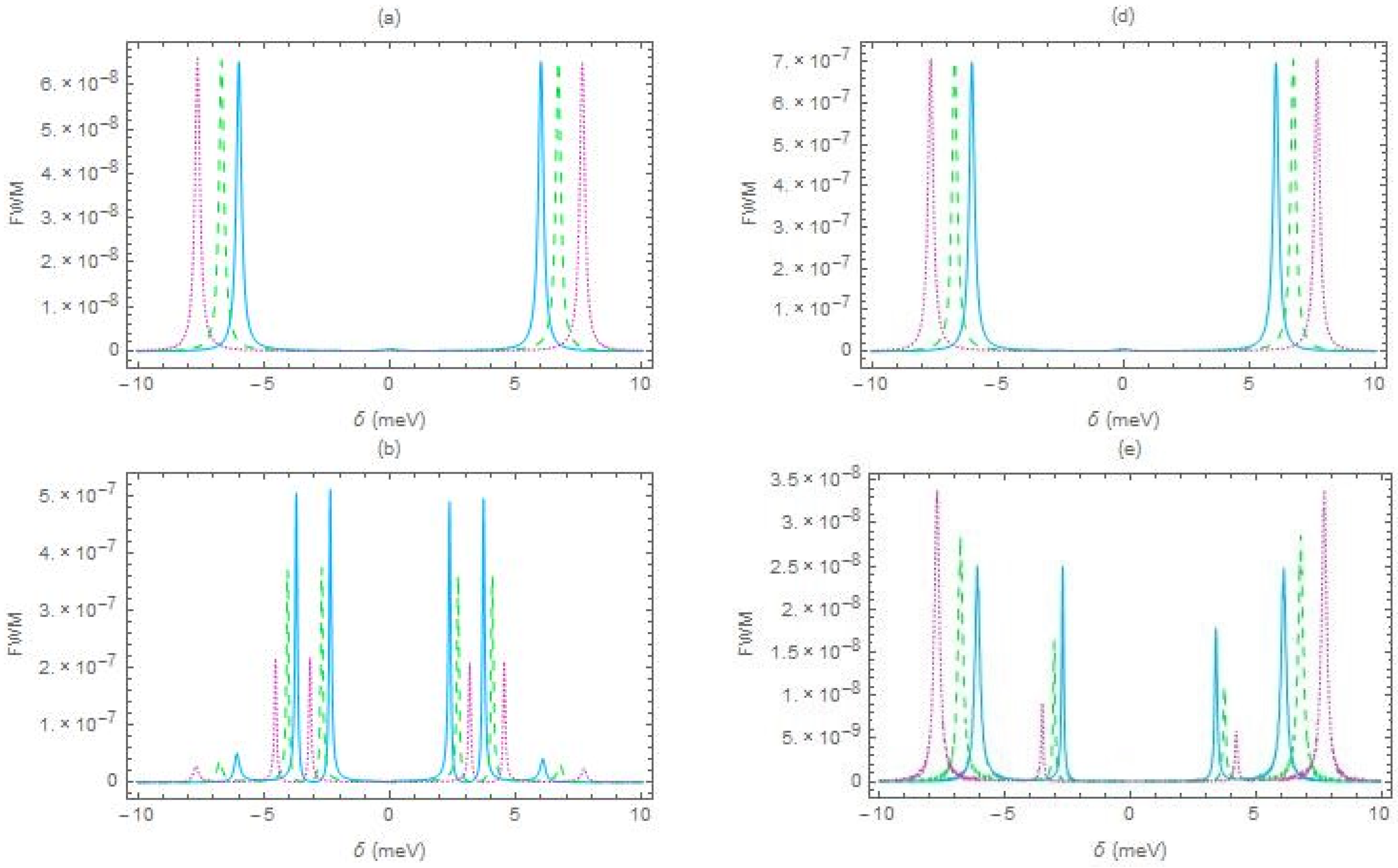
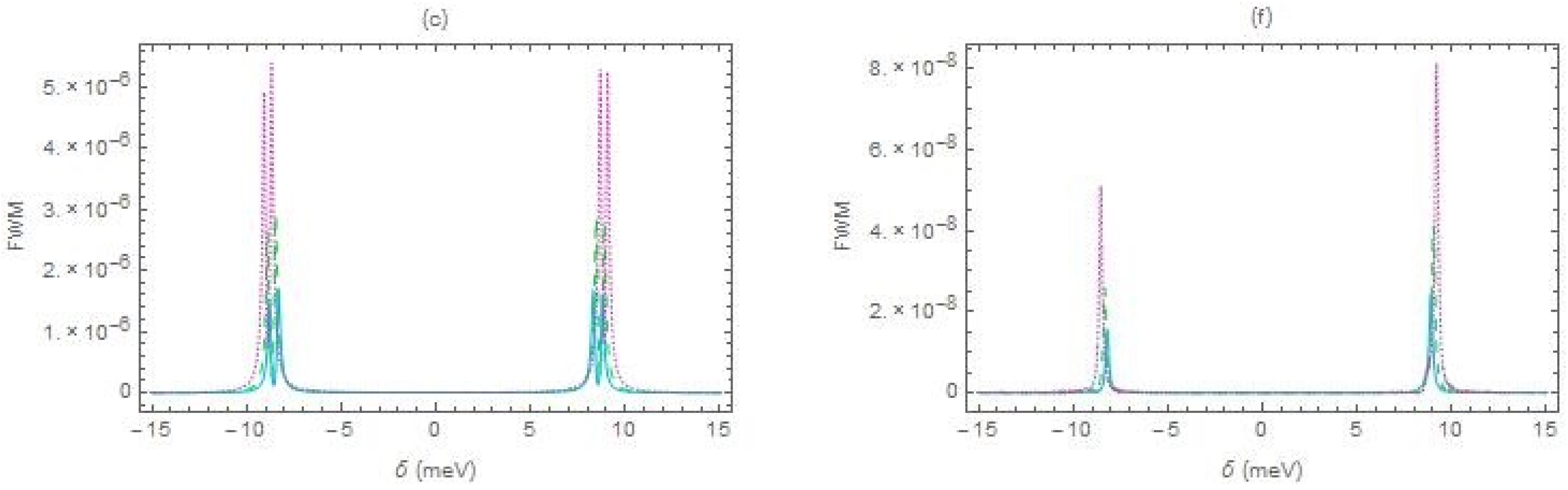
In the first column of Figure 2a–c, we present the FWM, as a function of the pump-probe field detuning $\delta ={\omega }_b-{\omega }_a$, for different interparticle distances [$R={100}_{}\mathrm{nm}$ (light blue solid curve), ${20}_{}\mathrm{nm}$ (green dashed curve) and ${15}_{}\mathrm{nm}$ (pink dotted curve)], in the case of exact pump-field resonance $\Delta =0$. In the second column of Figure 2d–f, we study the off-resonance case, with $\hslash {\omega }_{12}=\hslash \Delta ={0.7}_{}\mathrm{meV}$. In all cases, we consider that the energy difference between the levels $|1\rangle$ and $|2\rangle$, $\hslash {\omega }_{12}=\left({\mathrm{E}}_1-{\mathrm{E}}_2\right)$, is equal to ${0.7}_{}\mathrm{meV}$. In captions Figure 2a,d, we study the case of negligible tunneling rate $(\hslash T_e=0.01\mathrm{meV})$, while, in captions Figure 2b,e, we assume that $\hslash T_e=0.5\mathrm{meV}$, and in captions Figure 2c,f, we take $\hslash T_e=8\mathrm{meV}$.

4. Discussion

In the case of exact resonance Figure 2a–c, the FWM spectra are symmetric, with respect to the vertical axis at $\delta =0$, for every single value of the electron tunneling coefficient, for the specific value of the pump field Rabi frequency used. For a weak interparticle interaction (R > 100 nm), we observe a doublet of outer resonances approximately arising around $\pm 2\hslash \sqrt{{\Omega }_a^2+T_e^2}$, as well as a quadruplet of inner resonances, approximately arising around $\pm \hslash \sqrt{{\Omega }_a^2+T_e^2}$. In Figure 2a, with $\hslash T_e=0.01\mathrm{meV}$, the inner doublets are not noticeable, due to their low magnitude. On the other hand, in Figure 2c, with $\hslash T_e=8\mathrm{meV}$, the outer resonances are negligible. All the six resonance peaks appear on the FWM spectrum, for intermediate values of the tunneling rate, as seen in Figure 2b, with $\hslash T_e=0.5\mathrm{meV}$. In all these cases, the increase of the interparticle distance leads to a transposition of the resonances, toward higher values of the absolute pump–probe field detuning.

In the off-resonance case Figure 2d–f, the spectral symmetry is broken as long as the electron-tunneling coefficient is not negligible, as seen in Figure 2e,f, taken, respectively, for $\hslash T_e=0.5\mathrm{meV}$ and $\hslash T_e=8\mathrm{meV}$. We should note that the loss of symmetry is associated with the peaks arising at $\pm \hslash \sqrt{{\Omega }_a^2+T_e^2}$. In this case, since the dark-state condition $\hslash {\omega }_{12}=\hslash \Delta$ is accomplished, the six-peaked FWM spectrum is turned into a four-peaked spectrum. The rest spectral trends are similar to the ones presented in the previous case.

5. Summary

To summarize, we studied the FWM spectrum of a strongly pumped hybrid system, which is composed of an asymmetric double SQD molecule that is coupled to a spherical MNP, via long-range Coulomb interaction. In the case of a nonresonant pump field, with a pump-field detuning equal to the energy gap between the upper states of the Λ-type system, the spectra are approximately symmetric and exhibit four resonances, for average values of the electron-tunneling rate, since the dark-state condition is accomplished. However, in the case of exact resonance, the spectra are approximately asymmetric and exhibit a six-resonance profile. In any case, the increase of the center-to-center distance leads to a transposition of the resonances away from the spectral center.