In Silico Analysis of Microfluidic Systems for the Purification of Magnetoliposomes †
Abstract
:1. Introduction
2. Materials and Methods
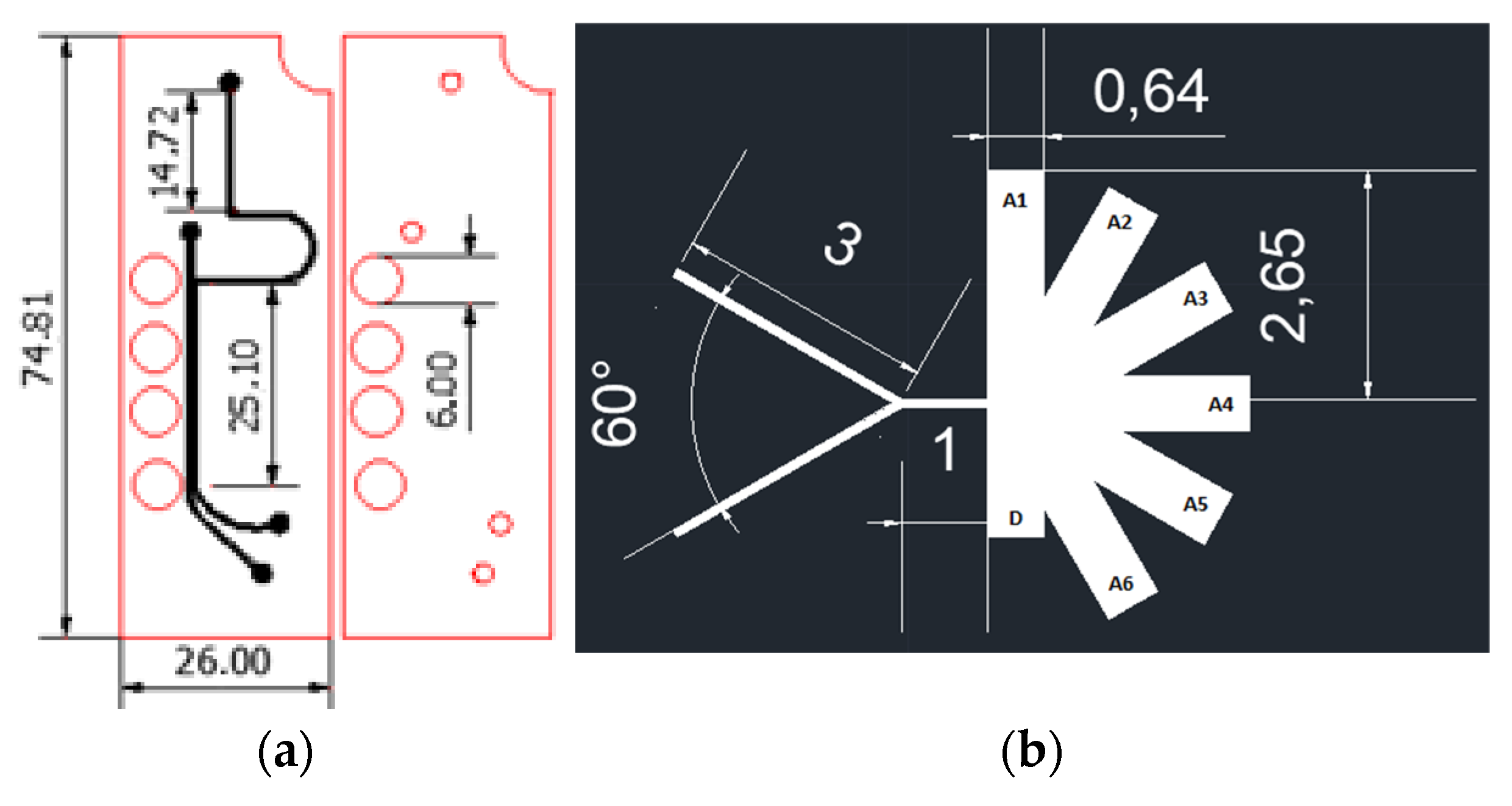
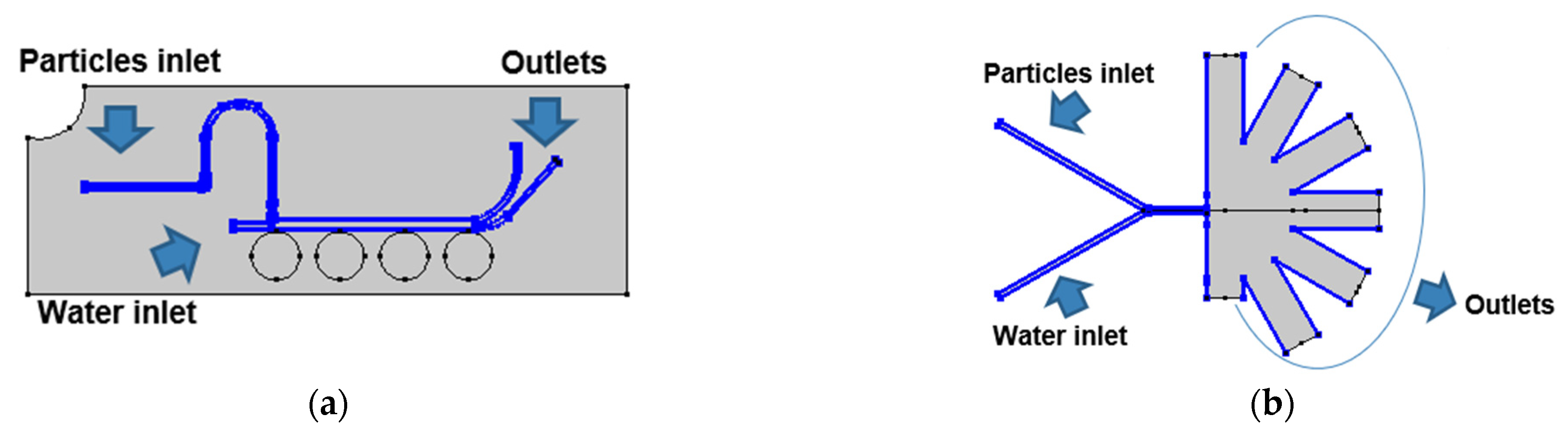
2.1. Microfluidic Systems Design
2.2. Simulation
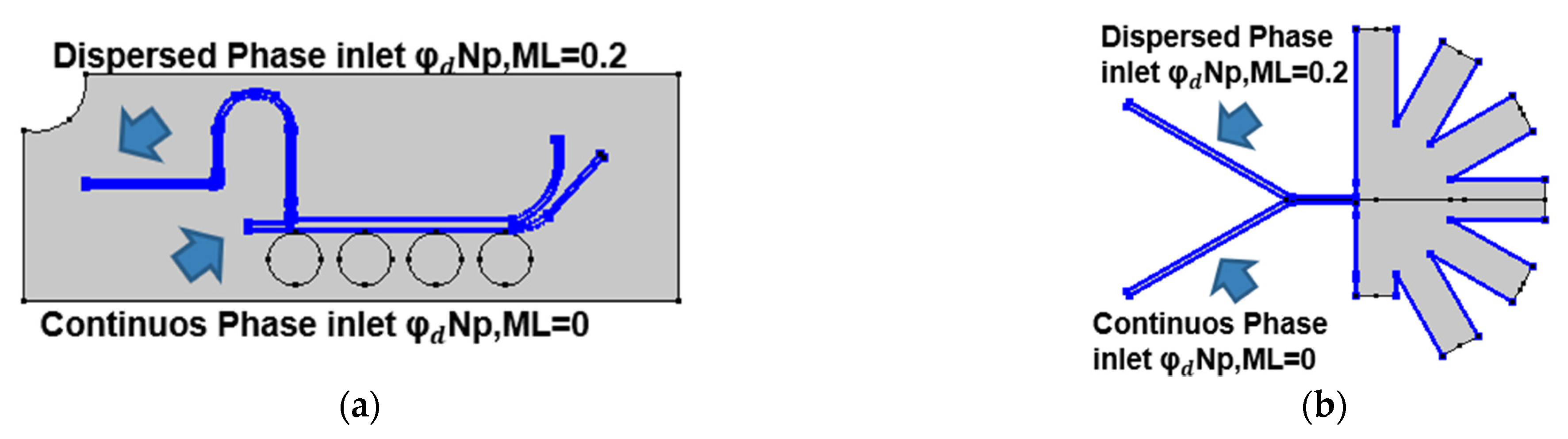
2.2.1. Particle Tracing Model
2.2.2. Mixture Model
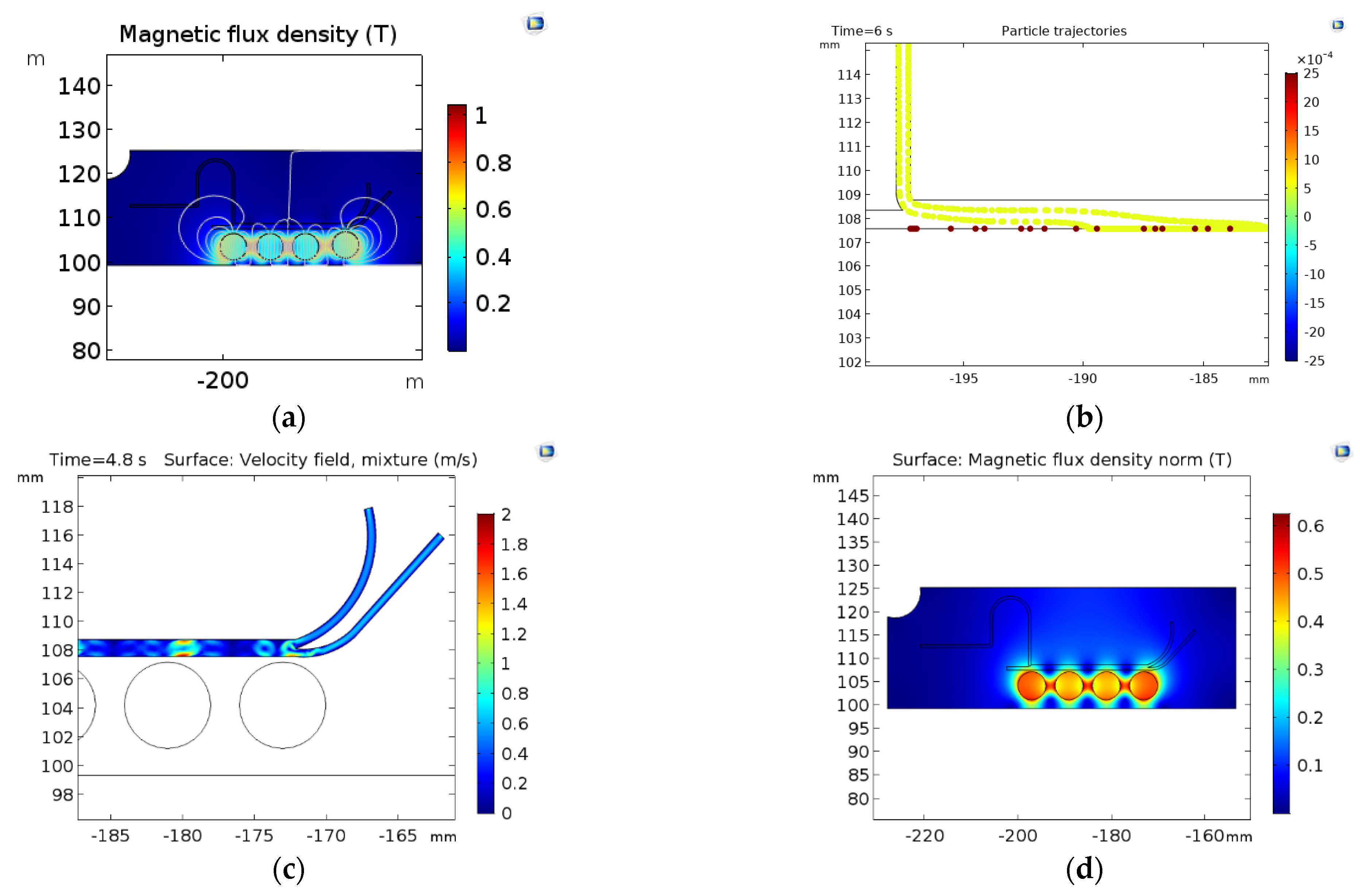
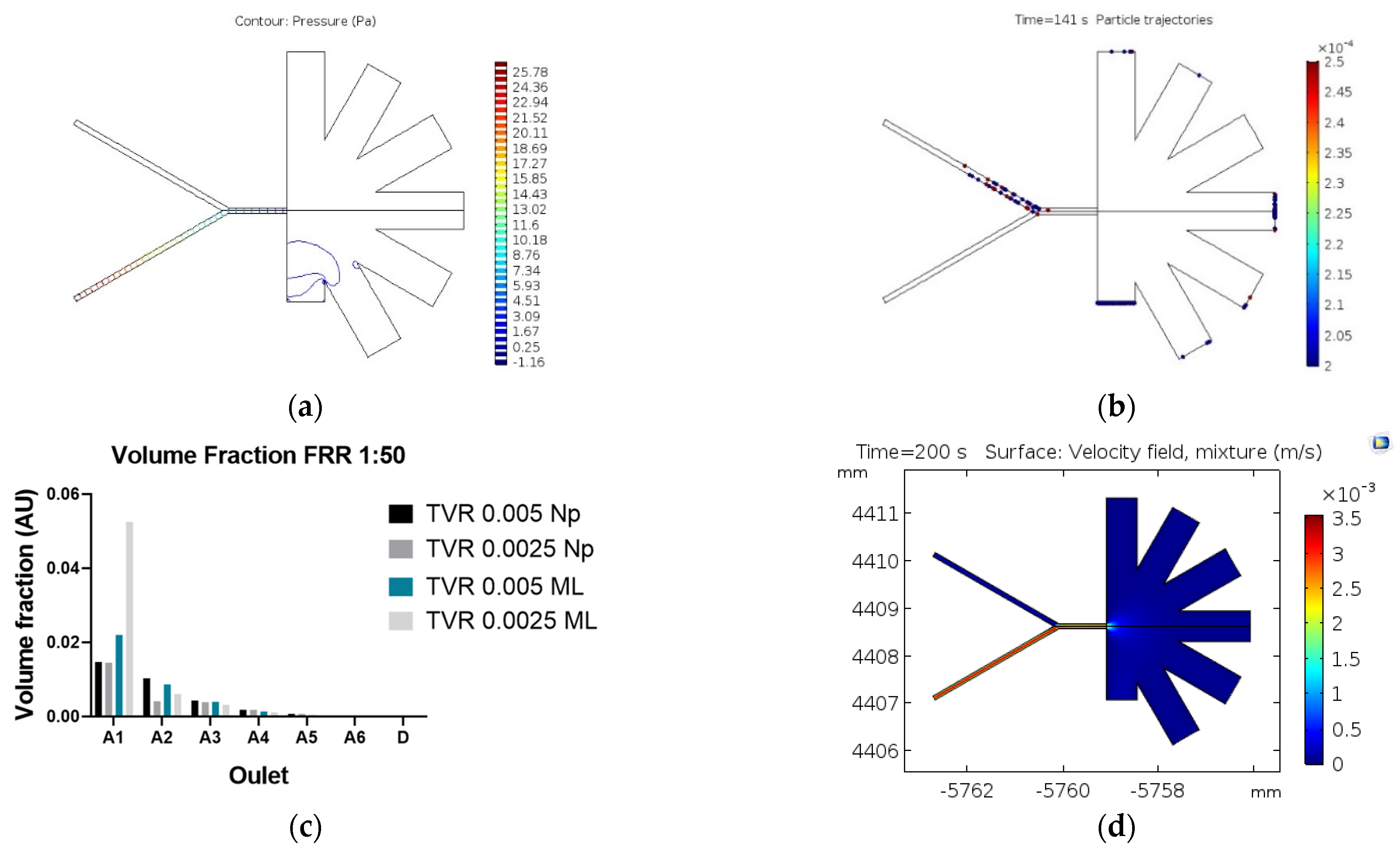
3. Results and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Choi, W.I.; Sahu, A.; Wurm, F.R.; Jo, S.M. Magnetoliposomes with size controllable insertion of magnetic nanoparticles for efficient targeting of cancer cells. RSC Adv. 2019, 9, 15053–15060. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Lu, Z.; Li, Y.; Yang, J.; Zhang, X. Surface modification of iron oxide-based magnetic nanoparticles for cerebral theranostics: Application and prospection. Nanomaterials 2020, 10, 1–21. [Google Scholar] [CrossRef] [PubMed]
- De Jesus, P.D.C.C.; Pellosi, D.S.; Tedesco, A.C. Magnetic Nanoparticles: Applications in Biomedical Processes as Synergic Drug-Delivery Systems; Elsevier Inc.: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Conde, A.J.; Batalla, M.; Cerda, B.; Mykhaylyk, O.; Plank, C.; Podhajcer, O.; Cabaleiro, J.M.; Madrid, R.E.; Policastro, L. Continuous flow generation of magnetoliposomes in a low-cost portable microfluidic platform. Lab Chip 2014, 14, 4506–4512. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, A.R.O.; Almeida, B.G.; Araújo, J.P.; Queiroz, M.J.R.P.; Coutinho, P.J.G.; Castanheira, E.M.S. Magnetoliposomes for dual cancer therapy. In Inorganic Frameworks as Smart Nanomedicines; William Andrew Publishing: Norwich, NY, USA, 2018. [Google Scholar]
- Rodrigues, A.R.O.; Gomes, I.T.; Almeida, B.G.; Araújo, J.P.; Castanheira, E.M.S.; Coutinho, P.J.G. Magnetoliposomes based on nickel/silica core/shell nanoparticles: Synthesis and characterization. Mater. Chem. Phys. 2014, 148, 978–987. [Google Scholar] [CrossRef]
- Bonnaud, C.; Monnier, C.A.; Demurtas, D.; Jud, C.; Vanhecke, D.; Montet, X.; Hovius, R.; Lattuada, M.; Rothen-Rutishauser, B.; Petri-Fink, A. Insertion of nanoparticle clusters into vesicle bilayers. ACS Nano 2014, 8, 3451–3460. [Google Scholar] [CrossRef] [PubMed]
- Floris, A.; Ardu, A.; Musinu, A.; Piccaluga, G.; Fadda, A.M.; Sinico, C.; Cannas, C. SPION@liposomes hybrid nanoarchitectures with high density SPION association. Soft Matter 2011, 7, 6239–6247. [Google Scholar] [CrossRef]
- Mota-Cobián, A.; Velasco, C.; Mateo, J. Optimization of purification techniques for lumen-loaded magnetoliposomes. Nanotechnology 2020, 31, 145102. [Google Scholar] [CrossRef] [PubMed]
- Joshi, S.; Hussain, M.T.; Roces, C.B.; Anderluzzi, G.; Kastner, E.; Salmaso, S.; Kirby, D.J.; Perrie, Y. Microfluidics based manufacture of liposomes simultaneously entrapping hydrophilic and lipophilic drugs. Int. J. Pharm. 2016, 514, 160–168. [Google Scholar] [CrossRef] [PubMed]
- Al-Ahmady, Z.S.; Donno, R.; Gennari, A.; Prestat, E.; Marotta, R.; Mironov, A.; Newman, L.; Lawrence, M.J.; Tirelli, N.; Ashford, M.; et al. Enhanced Intraliposomal Metallic Nanoparticle Payload Capacity Using Microfluidic-Assisted Self-Assembly. Langmuir 2019, 35, 13318–13331. [Google Scholar] [CrossRef] [PubMed]
- Takagi, J.; Yamada, M.; Yasuda, M.; Seki, M. Continuous particle separation in a microchannel having asymmetrically arranged multiple branches. Lab Chip 2005, 5, 778–784. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, N.; Martins, A.; Reis, R.L.; Neves, N.M. Liposomes in tissue engineering and regenerative medicine. J. R. Soc. Interface 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Kye, H.G.; Park, B.S.; Lee, J.M.; Song, M.G.; Song, H.G.; Ahrberg, C.D.; Chung, B.G. Dual-neodymium magnet-based microfluidic separation device. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Khashan, S.A.; Dagher, S.; Alazzam, A.; Mathew, B.; Hilal-Alnaqbi, A. Microdevice for continuous flow magnetic separation for bioengineering applications. J. Micromech. Microeng. 2017, 27. [Google Scholar] [CrossRef]
- Guo, J.; Lin, L.; Zhao, K.; Song, Y.; Huang, M.; Zhu, Z.; Zhou, L.; Yang, C. Auto-affitech: An automated ligand binding affinity evaluation platform using digital microfluidics with a bidirectional magnetic separation method. Lab Chip 2020, 20, 1577–1585. [Google Scholar] [CrossRef] [PubMed]
- Nakao, R.; Matuo, Y.; Mishima, F.; Taguchi, T.; Maenosono, S.; Nishijima, S. Development of magnetic separation system of magnetoliposomes. Phys. C Supercond. Appl. 2009, 469, 1840–1844. [Google Scholar] [CrossRef]
- Amiri, M.; Salavati-Niasari, M.; Akbari, A. Magnetic nanocarriers: Evolution of spinel ferrites for medical applications. Adv. Colloid Interface Sci. 2019, 265, 29–44. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, S.; Kumar, A.; Sen, P. Special Issue on Microfluidics: Theory and Applications. J. Indian Inst. Sci. 2018, 98, 83–84. [Google Scholar] [CrossRef]
- Barreto, G.R.; Kawai, C.; Tofanello, A.; Neves, A.A.R.; Araujo-Chaves, J.C.; Belleti, E.; Lanfredi, A.J.C.; Crespilho, F.N.; Nantes-Cardoso, I.L. Magnetoliposomes as model for signal transmission. R. Soc. Open Sci. 2019, 6. [Google Scholar] [CrossRef]
- Comsol Multiphysics. Mixer Module. 2015. Available online: http://www.comsol.com/mixer-module (accessed on 10 November 2020).
- Bergheau, J.M.; Fortunier, R. Finite Element Simulation of Heat Transfer. Finite Elem. Simul. Heat Transf. 2010. [Google Scholar] [CrossRef]
- Campaña, A.L.; Sotelo, D.C.; Oliva, H.A.; Aranguren, A.; Ornelas-Soto, N.; Cruz, J.C.; Osma, J.F. Fabrication and characterization of a low-cost microfluidic system for the manufacture of alginate-lacasse microcapsules. Polymers 2020, 12. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, C.E.; Aranguren, A.; Reyes, L.H.; Osma, J.F.; Cruz, J.C. In Silico Analysis of Microfluidic Systems for the Purification of Magnetoliposomes. Mater. Proc. 2021, 4, 73. https://doi.org/10.3390/IOCN2020-07794
Torres CE, Aranguren A, Reyes LH, Osma JF, Cruz JC. In Silico Analysis of Microfluidic Systems for the Purification of Magnetoliposomes. Materials Proceedings. 2021; 4(1):73. https://doi.org/10.3390/IOCN2020-07794
Chicago/Turabian StyleTorres, Carlos E., Andres Aranguren, Luis H. Reyes, Johann F. Osma, and Juan C. Cruz. 2021. "In Silico Analysis of Microfluidic Systems for the Purification of Magnetoliposomes" Materials Proceedings 4, no. 1: 73. https://doi.org/10.3390/IOCN2020-07794
APA StyleTorres, C. E., Aranguren, A., Reyes, L. H., Osma, J. F., & Cruz, J. C. (2021). In Silico Analysis of Microfluidic Systems for the Purification of Magnetoliposomes. Materials Proceedings, 4(1), 73. https://doi.org/10.3390/IOCN2020-07794








