Modeling and Simulation of Multiphase Flow for Nanoparticle Translocation †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Multiphysics Models
2.1.1. Mixture Model
2.1.2. Diluted Species Model
2.2. Modeling and Simulation
2.2.1. Computational Domain
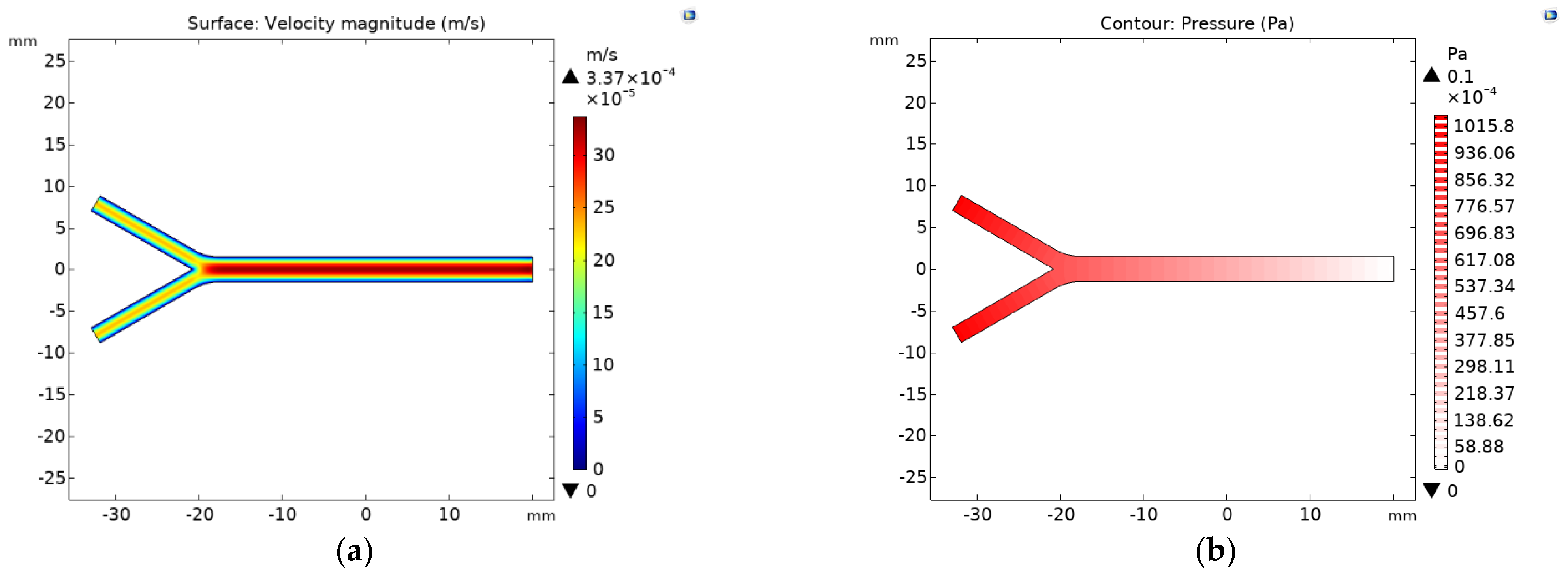
2.2.2. Velocity and Pressure Profile
2.2.3. Mesh
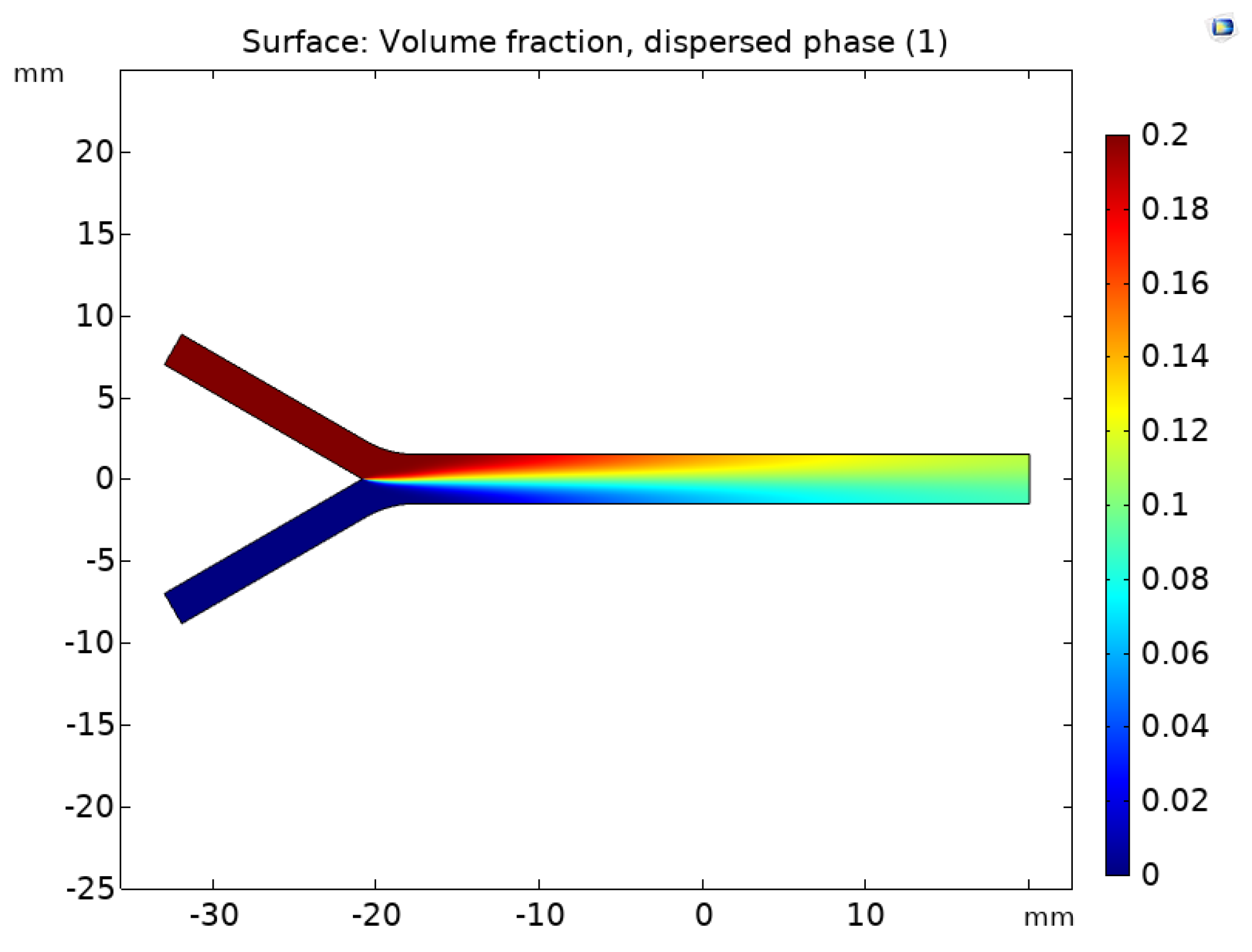
2.2.4. Mixture Model Implementation
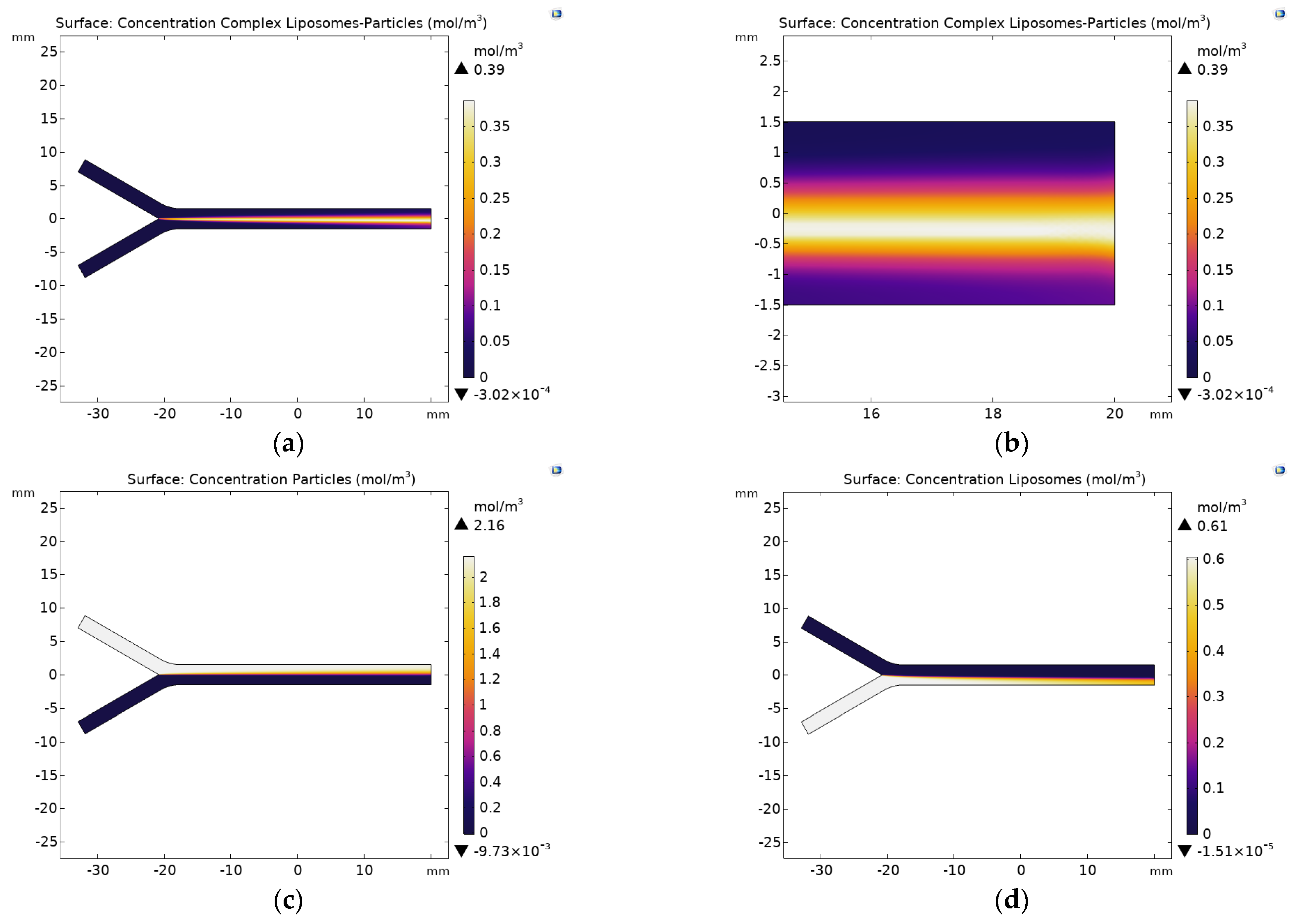
2.2.5. Diluted Species Model Implementation
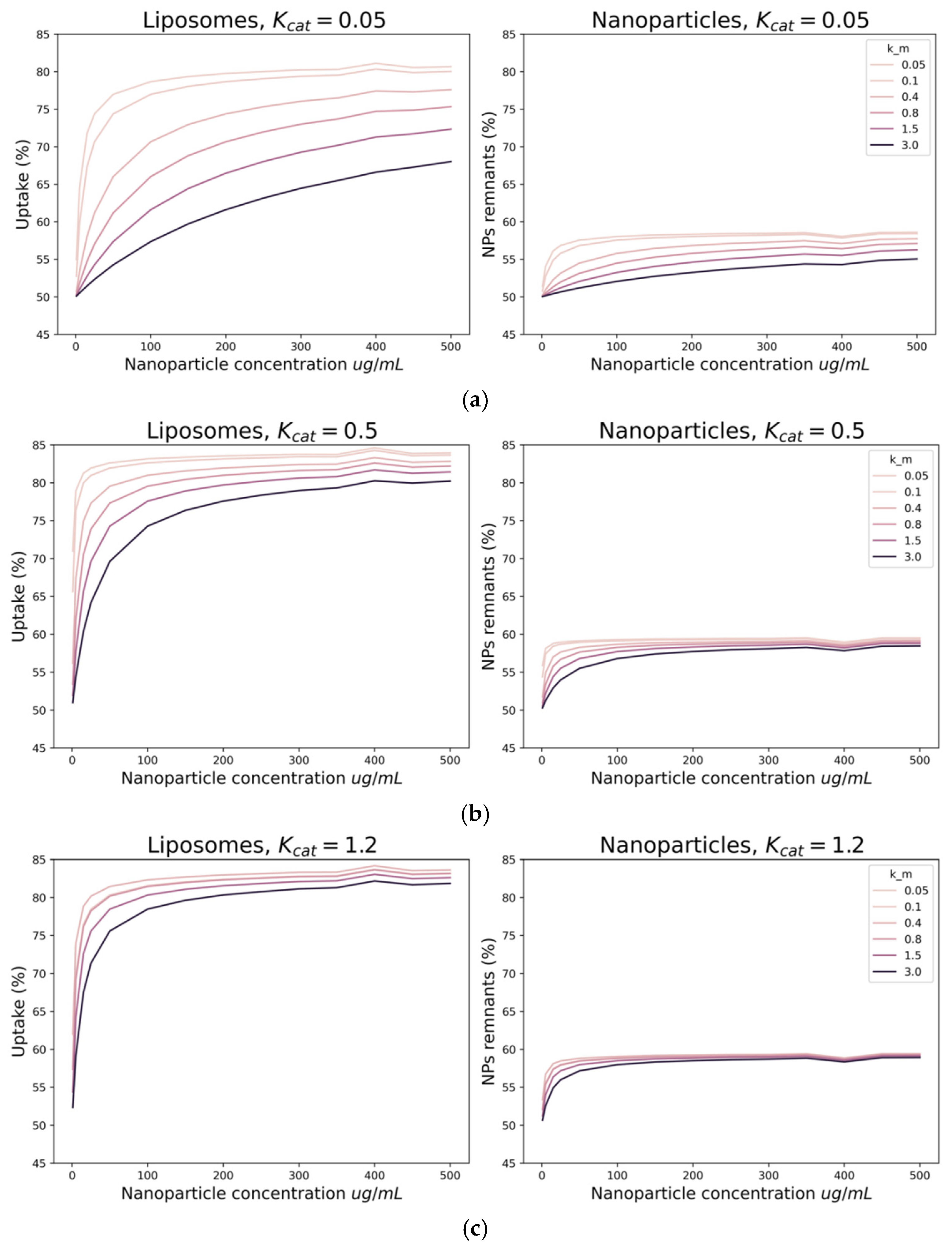
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Margus, H.; Padari, K.; Pooga, M. Cell-penetrating peptides as versatile vehicles for oligonucleotide delivery. Mol. Ther. 2012, 20, 525–533. [Google Scholar] [CrossRef] [PubMed]
- Juliano, R.L. Intracellular Trafficking and Endosomal Release of Oligonucleotides: What We Know and What We Don’t. Nucleic Acid Ther. 2018, 28, 166–177. [Google Scholar] [CrossRef]
- Ansari, S.A.M.K.; Ficiarà, E.; Ruffinatti, F.A.; Stura, I.; Argenziano, M.; Abollino, O.; Cavalli, R.; Guiot, C.; D’Agata, F. Magnetic iron oxide nanoparticles: Synthesis, characterization and functionalization for biomedical applications in the Central Nervous System. Materials 2019, 12, 465. [Google Scholar] [CrossRef]
- Allafchian, A.; Hosseini, S.S. Antibacterial magnetic nanoparticles for therapeutics: A review. IET Nanobiotechnol. 2019, 13, 786–799. [Google Scholar] [CrossRef] [PubMed]
- Malik, A.; Tahir Butt, T.; Zahid, S.; Zahid, F.; Waquar, S.; Rasool, M.; Qazi, M.H.; Qazi, A.M. Use of Magnetic Nanoparticles as Targeted Therapy: Theranostic Approach to Treat and Diagnose Cancer. J. Nanotechnol. 2017, 2017. [Google Scholar] [CrossRef]
- Lopez-Barbosa, N.; Suárez-Arnedo, A.; Cifuentes, J.; Gonzalez Barrios, A.F.; Silvera Batista, C.A.; Osma, J.F.; Munõz-Camargo, C.; Cruz, J.C. Magnetite-OmpA Nanobioconjugates as Cell-Penetrating Vehicles with Endosomal Escape Abilities. ACS Biomater. Sci. Eng. 2020, 6, 415–424. [Google Scholar] [CrossRef]
- Cuellar, M.; Cifuentes, J.; Perez, J.; Suarez-Arnedo, A.; Serna, J.A.; Groot, H.; Muñoz-Camargo, C.; Cruz, J.C. Novel BUF2-magnetite nanobioconjugates with cell-penetrating abilities. Int. J. Nanomed. 2018, 13, 8087–8094. [Google Scholar] [CrossRef]
- Perez, J.; Cifuentes, J.; Cuellar, M.; Suarez-Arnedo, A.; Cruz, J.C.; Muñoz-Camargo, C. Cell-penetrating and antibacterial BUF-II nanobioconjugates: Enhanced potency via immobilization on polyetheramine-modified magnetite nanoparticles. Int. J. Nanomed. 2019, 14, 8483–8497. [Google Scholar] [CrossRef]
- Alkayyali, T.; Cameron, T.; Haltli, B.; Kerr, R.G.; Ahmadi, A. Microfluidic and cross-linking methods for encapsulation of living cells and bacteria—A review. Anal. Chim. Acta 2019, 1053, 1–21. [Google Scholar] [CrossRef]
- Maeki, M.; Kimura, N.; Sato, Y.; Harashima, H.; Tokeshi, M. Advances in microfluidics for lipid nanoparticles and extracellular vesicles and applications in drug delivery systems. Adv. Drug Deliv. Rev. 2018, 128, 84–100. [Google Scholar] [CrossRef]
- Sercombe, L.; Veerati, T.; Moheimani, F.; Wu, S.Y.; Sood, A.K.; Hua, S. Advances and challenges of liposome assisted drug delivery. Front. Pharmacol. 2015, 6, 286. [Google Scholar] [CrossRef]
- Akbarzadeh, A.; Rezaei-Sadabady, R.; Davaran, S.; Joo, S.W.; Zarghami, N.; Hanifehpour, Y.; Samiei, M.; Kouhi, M.; Nejati-Koshki, K. Liposome: Classification, preparation, and applications. Nanoscale Res. Lett. 2013, 8, 102. [Google Scholar] [CrossRef] [PubMed]
- Yadav, D.; Sandeep, K.; Pandey, D.; Dutta, R.K. Liposomes for Drug Delivery. J. Biotechnol. Biomater. 2017, 07. [Google Scholar] [CrossRef]
- Gonzalez Gomez, A.; Syed, S.; Marshall, K.; Hosseinidoust, Z. Liposomal Nanovesicles for Efficient Encapsulation of Staphylococcal Antibiotics. ACS Omega 2019, 4, 10866–10876. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Bi, Y.; Zhang, H.; Dong, S.; Teng, L.; Lee, R.J.; Yang, Z. Cell-Penetrating Peptides in Diagnosis and Treatment of Human Diseases: From Preclinical Research to Clinical Application. Front. Pharmacol. 2020, 11, 697. [Google Scholar] [CrossRef] [PubMed]
- Pattni, B.S.; Chupin, V.V.; Torchilin, V.P. New Developments in Liposomal Drug Delivery. Chem. Rev. 2015, 115, 10938–10966. [Google Scholar] [CrossRef]
- Damiati, S.; Kompella, U.; Damiati, S.; Kodzius, R. Microfluidic Devices for Drug Delivery Systems and Drug Screening. Genes 2018, 9, 103. [Google Scholar] [CrossRef] [PubMed]
- Guimarães Sá Correia, M.; Briuglia, M.L.; Niosi, F.; Lamprou, D.A. Microfluidic manufacturing of phospholipid nanoparticles: Stability, encapsulation efficacy, and drug release. Int. J. Pharm. 2017, 516, 91–99. [Google Scholar] [CrossRef]
- Wen, N.; Zhao, Z.; Fan, B.; Chen, D.; Men, D.; Wang, J.; Chen, J. Development of droplet microfluidics enabling high-throughput single-cell analysis. Molecules 2016, 21, 881. [Google Scholar] [CrossRef] [PubMed]
- Van Swaay, D.; Demello, A. Microfluidic methods for forming liposomes. Lab Chip 2013, 13, 752–767. [Google Scholar] [CrossRef] [PubMed]
- Kumar, C.; Hejazian, M.; From, C.; Saha, S.C.; Sauret, E.; Gu, Y.; Nguyen, N.T. Modeling of mass transfer enhancement in a magnetofluidic micromixer. Phys. Fluids 2019, 31. [Google Scholar] [CrossRef]
- Oakey, J.; Applegate, R.W.; Arellano, E.; Carlo, D.D.; Graves, S.W.; Toner, M. Particle focusing in staged inertial microfluidic devices for flow cytometry. Anal. Chem. 2010, 82, 3862–3867. [Google Scholar] [CrossRef] [PubMed]
- Collins, D.J.; Ma, Z.; Han, J.; Ai, Y. Continuous micro-vortex-based nanoparticle manipulation via focused surface acoustic waves. Lab Chip 2017, 17, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Deshpande, S.; Birnie, A.; Dekker, C. On-chip density-based purification of liposomes. Biomicrofluidics 2017, 11, 034106. [Google Scholar] [CrossRef]
- Zhao, C. Microfluidic Nanoparticles Focusing and Separation Microfluidic Nanoparticles Focusing and Separation. Ph.D. Thesis, Lehigh University, Bethlehem, PA, USA, 2015. [Google Scholar]
- Mahian, O.; Kolsi, L.; Amani, M.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Peng, W.; Minli, B.; Jizu, L.; Chengzhi, H.; Yuyan, W. Numerical investigation on the turbulent flow characteristic of nanofluids in a horizontal circular tube. Numer. Heat Transf. Part A Appl. 2014, 66, 646–668. [Google Scholar] [CrossRef]
- COMSOL Multiphysics. CFD Module User’s Guide. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.cfd/CFDModuleUsersGuide.pdf (accessed on 10 October 2020).

| C0 Liposomes [mol/mL] | C0 MNPs [mol/mL] |
|---|---|
| 1.21 × 10−9 | 4.32 × 10−9 |
| 6.05 × 10−9 | 2.16 × 10−8 |
| 1.82 × 10−8 | 6.48 × 10−8 |
| 3.03 × 10−8 | 1.08 × 10−7 |
| 6.05 × 10−8 | 2.16 × 10−7 |
| 1.21 × 10−7 | 4.32 × 10−7 |
| 1.82 × 10−7 | 6.48 × 10−7 |
| 2.42 × 10−7 | 8.68 × 10−7 |
| 3.03 × 10−7 | 1.08 × 10−6 |
| 3.63 × 10−7 | 1.30 × 10−6 |
| 4.24 × 10−7 | 1.51 × 10−6 |
| 4.84 × 10−7 | 1.73 × 10−6 |
| 5.45 × 10−7 | 1.94 × 10−6 |
| 6.05 × 10−7 | 2.16 × 10−6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giraldo, K.A.; Bermudez, J.S.; Torres, S.; Reyes, L.H.; Osma, J.F.; Cruz, J.C. Modeling and Simulation of Multiphase Flow for Nanoparticle Translocation. Mater. Proc. 2021, 4, 71. https://doi.org/10.3390/IOCN2020-07796
Giraldo KA, Bermudez JS, Torres S, Reyes LH, Osma JF, Cruz JC. Modeling and Simulation of Multiphase Flow for Nanoparticle Translocation. Materials Proceedings. 2021; 4(1):71. https://doi.org/10.3390/IOCN2020-07796
Chicago/Turabian StyleGiraldo, Kevin A., Juan Sebastian Bermudez, Samuel Torres, Luis H. Reyes, Johann F. Osma, and Juan C. Cruz. 2021. "Modeling and Simulation of Multiphase Flow for Nanoparticle Translocation" Materials Proceedings 4, no. 1: 71. https://doi.org/10.3390/IOCN2020-07796
APA StyleGiraldo, K. A., Bermudez, J. S., Torres, S., Reyes, L. H., Osma, J. F., & Cruz, J. C. (2021). Modeling and Simulation of Multiphase Flow for Nanoparticle Translocation. Materials Proceedings, 4(1), 71. https://doi.org/10.3390/IOCN2020-07796











