Abstract
The encapsulation of biomolecules and microorganisms into liposomes is useful for several biological and biomedical applications. For instance, it is possible to encapsulate pharmacological compounds to increase properties such as therapeutic effectiveness, circulation times, and biocompatibility. Here, we are interested in encapsulating yeast cells expressing translocating peptide molecules on their surfaces. This is with the final intention of separating yeasts with translocating activity from those with other types of membrane activities. To accomplish this, we designed a microfluidic system for the synthesis of giant liposomes (100–150 µm in diameter) based on the droplet generation of double emulsions (water-in-oil-in-water) as templates. Giant liposomes were selected here due to their size, lipid structure (unilamellar), and the ability to control the internal content, which closely mimics, albeit in a more simplified manner, the structural organization of living cells. The microfluidic device comprises a W/O/W junction equipped with three sets of inlets, the main channel, and an output channel at an angle of 30°. The system’s performance was evaluated in silico by implementing a Two-Phase Flow, Level Set model where the flow rate ratios of the continuous and dispersed phases were altered until the droplet was formed. Next, interaction with yeasts was achieved by a Y-junction geometry with two 0.5-mm-length inlets at 45°. The interaction was simulated with the aid of a Mixture Model. Maximum velocity was obtained at the center of the channel and complete mixing at the outlet, indicating high interaction levels. Finally, we implemented an inertial geometry using a Particle Tracing Flow Focusing Model to study the molecules’ separation.
1. Introduction
Microencapsulation has attracted considerable attention from the cosmetics, food, and pharma industries, mainly due to the possibility to protect functional and valuable compounds from harsh environments [1,2]. Additionally, they offer a route to ensure that the encapsulated compounds can be released in a controlled manner [3,4]. There are many materials to produce encapsulates, including phospholipids (e.g., liposomes), natural (e.g., inulin, gum arabic, alginate, starch) and synthetic (e.g., poly-methyl methacrylate, Acrolein, polyamide) polymers, and biopolymers (e.g., cellulose, gelatin, collagen) [5,6,7,8,9,10,11]. Moreover, several methods are readily available to form such encapsulates, including solvent evaporation, ionic gelation, coacervation, and emulsification [3,12,13,14,15]. Despite this ample range of strategies, the most mature manufacture methods offer poor control of morphology, size distribution, and porosity [16]. These have limited their full implementation at a large scale [17]. Alternatively, microfluidic devices offer the possibility to manipulate objects at the microscale while using minimal volumes of fluids, and by implementing processes that include pumping, metering, mixing, separation, and droplet generation [18]. In this regard, monodispersed microcapsules of different materials can be effectively prepared via droplet-based microfluidics. In this approach, the microcapsules are generated by placing into contact two immiscible phases. The size and dispersion of the obtained materials is controlled by finely tuning the microchannel geometries and flow rates [19,20] Some successful examples of the implementation of this technology include the synthesis of microcapsules from numerous polymers including gelatin, cellulose, alginate, and chitosan [21,22]. Additionally, these devices proved useful for the synthesis of liposomes, with sphere-shaped vesicles consisting of one (unilamellar) or more phospholipid bilayers (multilamellar), ranging from tens of nanometers to tens of micrometers in diameter. Recently, shear-focusing-based droplet microfluidic systems have enabled the production of giant liposomes or giant unilamellar vesicles (GUVs) [23]. The obtained GUVs exhibited diameters in the range of 1–200 µm.
GUVs are primarily used because they exhibit a set of physical features—size, lipid structure (unilamellar), and the ability to control the internal content—that closely mimic, albeit in a more simplified manner, the structural organization of living cells. These unique characteristics can be further exploited to study the interaction of the cell membrane with different molecules ranging from pharmacological principles to membrane proteins [24]. Over the past two years, we have been working on the development of a novel, non-rational library of peptides, and in order to search for the ones with translocating activity, we proposed to conduct a screening with the aid of GUVs. In this regard, the peptides will be expressed superficially via yeast surface display and subsequently placed in contact with GUVs. If the expressed peptides show translocating activity, they will be able to move across the membrane of the GUV to become encapsulated. An important challenge is therefore to find strategies to separate the loaded GUVs from the empty ones.
Here, a microfluidic system was designed and simulated in COMSOL Multiphysics aided by a Two-Phase flow, Level set model where the flow rate ratio (FRR) and the total flow rate (TFR) of the continuous and dispersed phases were varied until the droplet was formed to synthesize double emulsion W/O/W templates. This was intended to ultimately produce GUVs of 100–150 µm by dewetting and evaporation of the solvent. For the encapsulation of yeasts expressing the translocating peptides, a Mixture Model simulation was carried out to estimate the role of key parameters in the interaction between GUVs and yeasts. Finally, an inertial focusing geometry was designed and tested in silico via the particle tracing module of COMSOL Multiphysics for the precise separation of loaded GUVs.
2. Materials and Methods
2.1. Microfluidic System Design
The design of the three systems studied here (i.e., GUV generator, droplet-based encapsulating device, and loaded GUV separator) is shown in Figure 1. The micromixer geometry for droplet encapsulation consists of a Y junction with a serpentine channel, as proposed previously by Kitson et al. [25], while the inertial design for separation was proposed by Garcia and Pennathur [26].
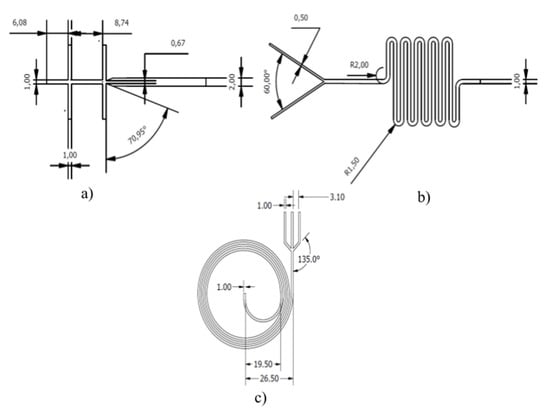
Figure 1.
Design dimensions (mm) of the microsystems. (a) The WOW junction, (b) the Y junction with a serpentine structure, and (c) the inertial snail design.
2.2. Simulation
The computational simulations were carried out employing the software COMSOL Multiphysics. For the simulation of the double emulsion templates, the Two-Phase Flow, Level Set module was used as this multiphysics coupling feature defines the density and dynamic viscosity of the fluid used in the Laminar Flow interface. Moreover, it describes the surface tension at the interface by incorporating a volume force into the momentum equation. It also enables the Level Set interface to use the velocity field calculated from the Laminar Flow module for the movement of the interface. By default, the Level Set interface use the incompressible formulation of the Navier–Stokes momentum Equation (1) and a continuity Equation (2),
where 𝜌 is the density, u is the velocity vector, p is the pressure, I is the intensity vector, µ is the dynamic viscosity, Fg is the gravity force vector, Fst is the surface tension force vector, Fext is the user-defined volume force vector, and F is the volume force vector. To track the movement of the interface, it adds the following Equation (3),
where ϕ can represent any scalar quantity of the flow, 𝛾 is the reinitialization parameter (set to 1 by default), and ε is the interface thickness controlling parameter. Continuous and disperse phases enter the channel by inlets 1 and 3 (left and right) for the former and inlet 2 (center) for the latter, with an initial velocity of 0.02 m/s for water and oil, and 0.06 m/s for the second inlet of water. The model considers no slip and no flow boundary conditions at the walls of the device for Laminar Flow and Level Set simulations, respectively. The simulation was carried out as a time-dependent study for a computational domain discretized with a fine mesh that consisted of 2444 domain elements and 432 boundary elements. This discretization level proved to lead to convergence (data not shown).
The mixture of the dispersed and continuous phases was simulated via a Mixture Model. In the Mixture Model interfaces, the particle–fluid combination is regarded as a single flowing continuum with macroscopic properties such as density and viscosity. The Mixture Model interface solves one set of Navier–Stokes equations for the mixture’s momentum defined in Equation (4).
where j is the velocity vector, ε is the reduced density difference, uslip is the slip velocity vector between the two phases, jslip is the slip flux. Moreover, the volume fraction of the dispersed phase is tracked by solving the transport Equation (5):
The Mixture Model contemplates continuous and dispersed phases modeled as saline solution with an initial velocity of 0.01 m/s for each. The dispersed phase was characterized as liquid droplets/bubbles with a dispersed fraction (ϕ) equal to 0.2 and a no slip boundary condition for the wall of the geometry. The simulation was carried out with a mesh consisting of 11,967 domain elements, 1615 boundary elements, and a time-dependent study for 10 s.
For the separation of the particles, a Particle Tracing Flow Focusing Model was used. The trajectories were computed in the time domain by solving a set of equations based on Newton’s second law, which states that the net force on an object is equal to the time derivative of its linear momentum in an inertial reference frame, which is described by Equations (6) and (7).
where mp is the particle mass, v is the particle velocity, and q is the particle position. Yeasts and loaded GUVs were modeled as solid particles of 10 μm and 100 μm, respectively, considering no slip, drag, and lift forces acting over all the particles as boundary conditions. The simulation was carried out with a mesh consisting of 2887 domain elements and 1775 boundary elements, and a time-dependent study for 60 s.
3. Results
The simulation results for the three models are shown in Figure 2. The geometry proposed (see Figure 1a) allowed us to determine the effect of TFR and FRR on the droplet size and generation. As presented in Figure 2a, the volume fraction evidenced the generation of large and stable double emulsion droplets at a reasonable rate in the outlet channel for the studied simulation parameters. According to the volume fraction of the dispersed phase from the Mixture Model (Figure 2b), it appears that the mixing of phases is homogeneous, thereby indicating significant possibilities of interaction between GUV and yeasts. Finally, Figure 2c shows that the inertial geometry allows high-efficiency separation of loaded liposomes from the rest of components, as they exit the system through different outlets. In the case of loaded liposomes, the particles (100 µm) exited the system through outlets 1 and 2, while yeasts, modeled as 10-µm-diameter particles, can be recovered in outlet 3.
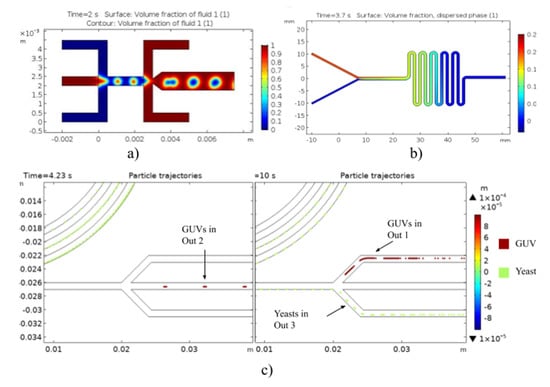
Figure 2.
Multiphysics simulation results of the microfluidic system for (a) volume fraction of double emulsions as templates for the synthesis of GUVs, (b) volume fraction of the Mixture Model for the interaction between giant liposomes and translocating peptide expressing yeasts, and (c) particle trajectories for the separation of loaded liposomes.
4. Discussion
First, Two-Phase Flow, Level Set model results showed that the droplet size is reduced by increasing the continuous phase’s velocity. Likewise, by increasing the velocity of the dispersed phase, the generation rate of the droplets is increased. In addition, the cross-sectional reduction at the double emulsion formation intersection and its subsequent expansion led to an increase in the size and stability of the produced droplets (Figure 2a). The volume fraction of the dispersed phase from the Mixture Model (Figure 2b) shows that the dispersed phase mixes effectively with the continuous phase. This allowed us to conclude that the GUVs and yeasts will have sufficient interaction events along the multiple turns of the device. Finally, the proposed inertial separation system showed promising results and significant specificity for separating loaded liposomes from the yeasts in the mixture. The results indicated a separation efficiency of approximately 70% considering 100% precision and 53% recall for loaded GUVs, which exited the systems through outlets 1 and 2, completely isolated from the yeasts with expressed peptides without membrane-translocation activity. The recall decrease can be attributed to liposomes exiting the system unexpectedly through a non-specific channel. Therefore, it is also necessary to consider the possibility that non-loaded liposomes could be collected in the same outlets, decreasing the system’s performance. For future work, we expect to increase the accuracy of the model by including a third particle type to account for empty liposomes. Moreover, it is important to include the actual densities of both empty and loaded liposomes, which requires experimental analysis.
Author Contributions
Conceptualization, J.C.C., J.F.O. and L.H.R.; Methodology, data curation, and data analysis S.C.G., V.Q. and J.C.C.; Formal analysis and investigation, S.C.G. and V.Q.; Validation, J.C.C., J.F.O. and L.H.R.; Writing—original draft preparation, S.C.G., V.Q.; Writing—review and editing, J.C.C., J.F.O. and L.H.R.; Supervision, J.C.C., J.F.O. and L.H.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Colombian Ministry of Science, Technology, and Innovation (Minciencias) Grants 689-2018, and ID 120380763212—PPTA # 8352.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Acknowledgments
The authors would like to thank the Department of Biomedical Engineering, the Department of Food and Chemical Engineering and the Department of Electrical & Electronics Engineering at Universidad de Los Andes for the financial and technical support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Paulo, F.; Santos, L. Design of experiments for microencapsulation applications: A review. Mater. Sci. Eng. C 2017, 77, 327–1340. [Google Scholar] [CrossRef] [PubMed]
- Hendrawati, T.Y.; Sari, A.M.; Rahman, M.I.S.; Nugrahani, R.A.; Siswahyu, A. Microencapsulation Techniques of Herbal Compounds for Raw Materials in Food Industry, Cosmetics and Pharmaceuticals. Microencapsul. Process. Technol. Ind. Appl. 2019, 1–15. [Google Scholar] [CrossRef]
- Ozkan, G.; Franco, P.; de Marco, I.; Xiao, J.; Capanoglu, E. A review of microencapsulation methods for food antioxidants: Principles, advantages, drawbacks and applications. Food Chem. 2019, 272, 494–506. [Google Scholar] [CrossRef] [PubMed]
- Ye, Q.; Georges, N.; Selomulya, C. Microencapsulation of active ingredients in functional foods: From research stage to commercial food products. Trends Food Sci. Technol. 2018, 78, 167–179. [Google Scholar] [CrossRef]
- Shishir, M.R.I.; Xie, L.; Sun, C.; Zheng, X.; Chen, W. Advances in micro and nano-encapsulation of bioactive compounds using biopolymer and lipid-based transporters. Trends Food Sci. Technol. 2018, 78, 34–60. [Google Scholar] [CrossRef]
- De Barros Fernandes, R.V.; Botrel, D.A.; Silva, E.K.; Borges, S.V.; de Oliveira, C.R.; Yoshida, M.I.; de Andrade Feitosa, J.P.; de Paula, R.C.M. Cashew gum and inulin: New alternative for ginger essential oil microencapsulation. Carbohydr. Polym. 2016, 153, 133–142. [Google Scholar] [CrossRef]
- Hoyos-Leyva, J.D.; Bello-Pérez, L.A.; Alvarez-Ramirez, J.; Garcia, H.S. Microencapsulation using starch as wall material: A review. Food Rev. Int. 2018, 34, 148–161. [Google Scholar] [CrossRef]
- Pieczykolan, E.; Kurek, M.A. Use of guar gum, gum arabic, pectin, beta-glucan and inulin for microencapsulation of anthocyanins from chokeberry. Int. J. Biol. Macromol. 2019, 129, 665–671. [Google Scholar] [CrossRef]
- Suganya, V.; Anuradha, V. Microencapsulation and Nanoencapsulation: A Review. Int. J. Pharm. Clin. Res. 2017, 9, 233–239. [Google Scholar] [CrossRef]
- Mu, R.J.; Yuan, Y.; Wang, L.; Ni, Y.; Li, M.; Chen, H.; Pang, J. Microencapsulation of Lactobacillus acidophilus with konjac glucomannan hydrogel. Food Hydrocoll. 2018, 76, 42–48. [Google Scholar] [CrossRef]
- Sharif, N.; Khoshnoudi-Nia, S.; Jafari, S.M. Nano/microencapsulation of anthocyanins; a systematic review and meta-analysis. Food Res. Int. 2020, 132, 109077. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Wang, S.; Wang, Y.; Liu, H.; Huo, X.; Ma, H.; Ma, Z.; Xiong, H. Microencapsulation of oxalic acid via oil-in-oil (O/O) emulsion solvent evaporation. Powder Technol. 2017, 320, 405–411. [Google Scholar] [CrossRef]
- Otálora, M.C.; Carriazo, J.G.; Iturriaga, L.; Osorio, C.; Nazareno, M.A. Encapsulating betalains from Opuntia ficus-indica fruits by ionic gelation: Pigment chemical stability during storage of beads. Food Chem. 2016, 202, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Timilsena, Y.P.; Akanbi, T.O.; Khalid, N.; Adhikari, B.; Barrow, C.J. Complex coacervation: Principles, mechanisms and applications in microencapsulation. Int. J. Biol. Macromol. 2019, 121, 1276–1286. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Shang, Y.; Zhu, Y.; Zhang, X.; Jingjing, E.; Zhao, L.; Wang, J. Study on microencapsulation of Lactobacillus plantarum LIP-1 by emulsification method. J. Food Process Eng. 2020, 43. [Google Scholar] [CrossRef]
- Zhang, Y.; Rochefort, D. Characterisation and applications of microcapsules obtained by interfacial polycondensation. J. Microencapsul. 2012, 29, 636–649. [Google Scholar] [CrossRef]
- Campaña, A.L.; Sotelo, D.C.; Oliva, H.A.; Aranguren, A.; Ornelas-Soto, N.; Cruz, J.C.; Osma, J.F. Fabrication and characterization of a low-cost microfluidic system for the manufacture of alginate-lacasse microcapsules. Polymers 2020, 12, 1158. [Google Scholar] [CrossRef]
- Lee, S.; Sundararajan, N. Microfabrication and Microfluidics; Artech House: Boston, MA, USA, 2010. [Google Scholar]
- Kastner, E.; Kaur, R.; Lowry, D.; Moghaddam, B.; Wilkinson, A.; Perrie, Y. High-throughput manufacturing of size-tuned liposomes by a new microfluidics method using enhanced statistical tools for characterization. Int. J. Pharm. 2014, 477, 361–368. [Google Scholar] [CrossRef]
- Trantidou, T.; Friddin, M.S.; Salehi-Reyhani, A.; Ces, O.; Elani, Y. Droplet microfluidics for the construction of compartmentalised model membranes. Lab Chip 2018, 18, 2488–2509. [Google Scholar] [CrossRef]
- Fang, A.; Cathala, B. Smart swelling biopolymer microparticles by a microfluidic approach: Synthesis, in situ encapsulation and controlled release. Colloids Surf. B Biointerfaces 2011, 82, 81–86. [Google Scholar] [CrossRef]
- Matalanis, A.; Jones, O.G.; McClements, D.J. Structured biopolymer-based delivery systems for encapsulation, protection, and release of lipophilic compounds. Food Hydrocoll. 2011, 25, 1865–1880. [Google Scholar] [CrossRef]
- Tan, Y.C.; Hettiarachchi, K.; Siu, M.; Pan, Y.R.; Lee, A.P. Controlled microfluidic encapsulation of cells, proteins, and microbeads in lipid vesicles. J. Am. Chem. Soc. 2006, 128, 5656–5658. [Google Scholar] [CrossRef] [PubMed]
- Matosevic, S. Synthesizing artificial cells from giant unilamellar vesicles: State-of-the art in the development of microfluidic technology. BioEssays 2012, 34, 992–1001. [Google Scholar] [CrossRef]
- Kitson, P.J.; Rosnes, M.H.; Sans, V.; Dragone, V.; Cronin, L. Configurable 3D-Printed millifluidic and microfluidic ‘lab on a chip’ reactionware devices. Lab Chip 2012, 12, 3267–3271. [Google Scholar] [CrossRef] [PubMed]
- Garcia, M.; Pennathur, S. A model for inertial particles in curvilinear flows. Microfluid. Nanofluid. 2019, 23, 1–9. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).