Resonant Mode Coupling Method for the Description of Oscillating Dipoles Emission inside Stacked Photonic Nanostructures †
Abstract
:1. Introduction
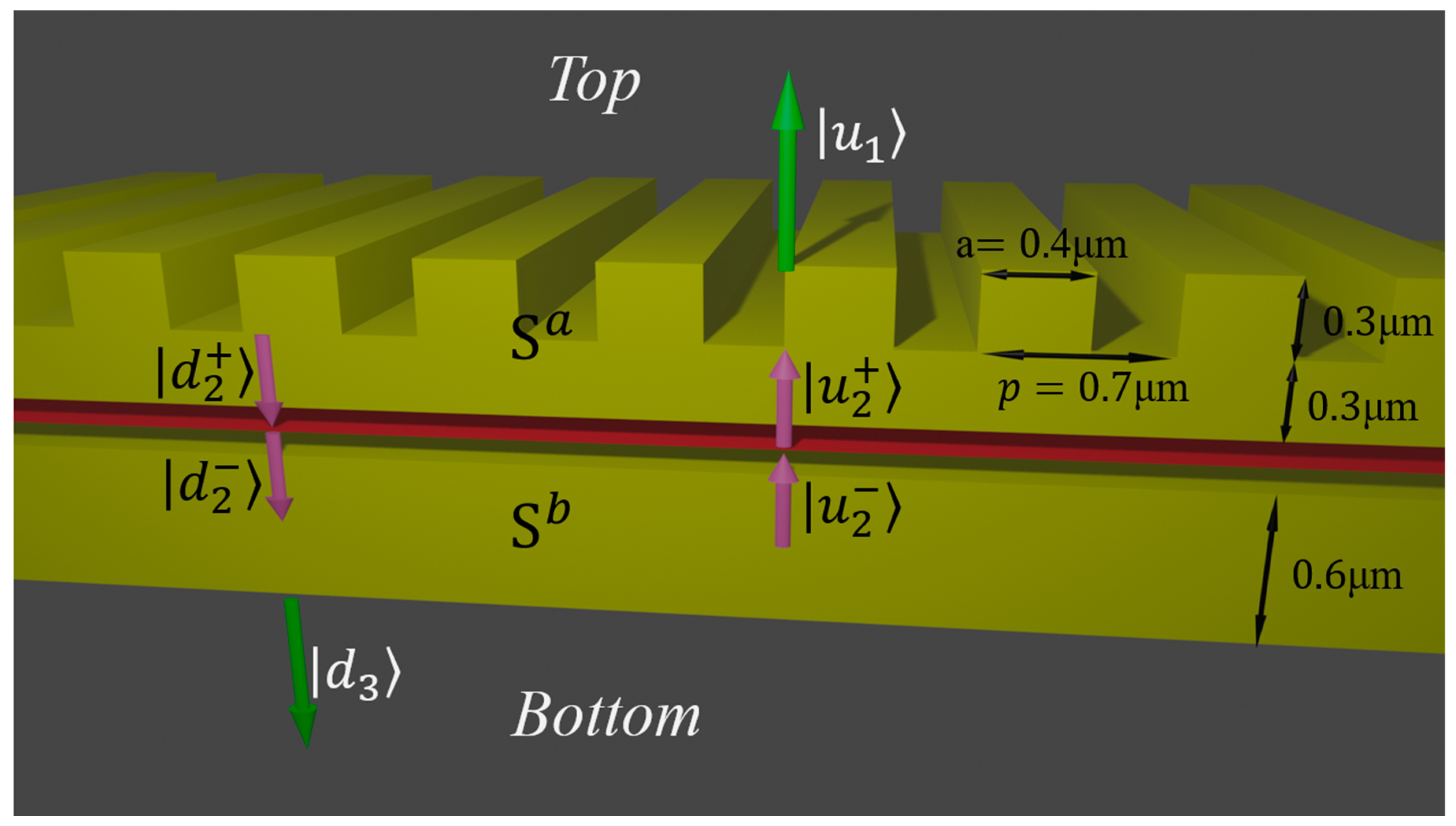
2. Methods
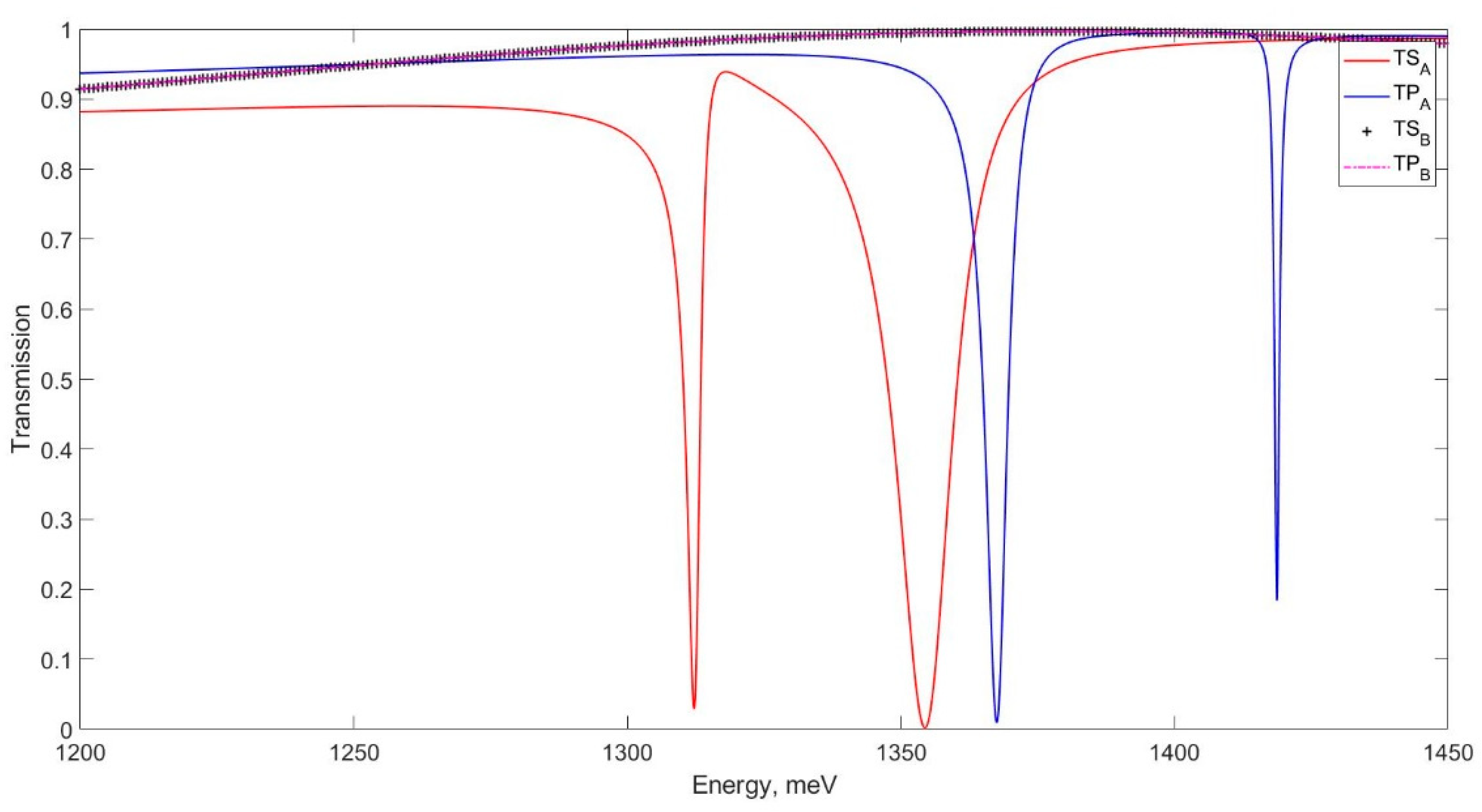
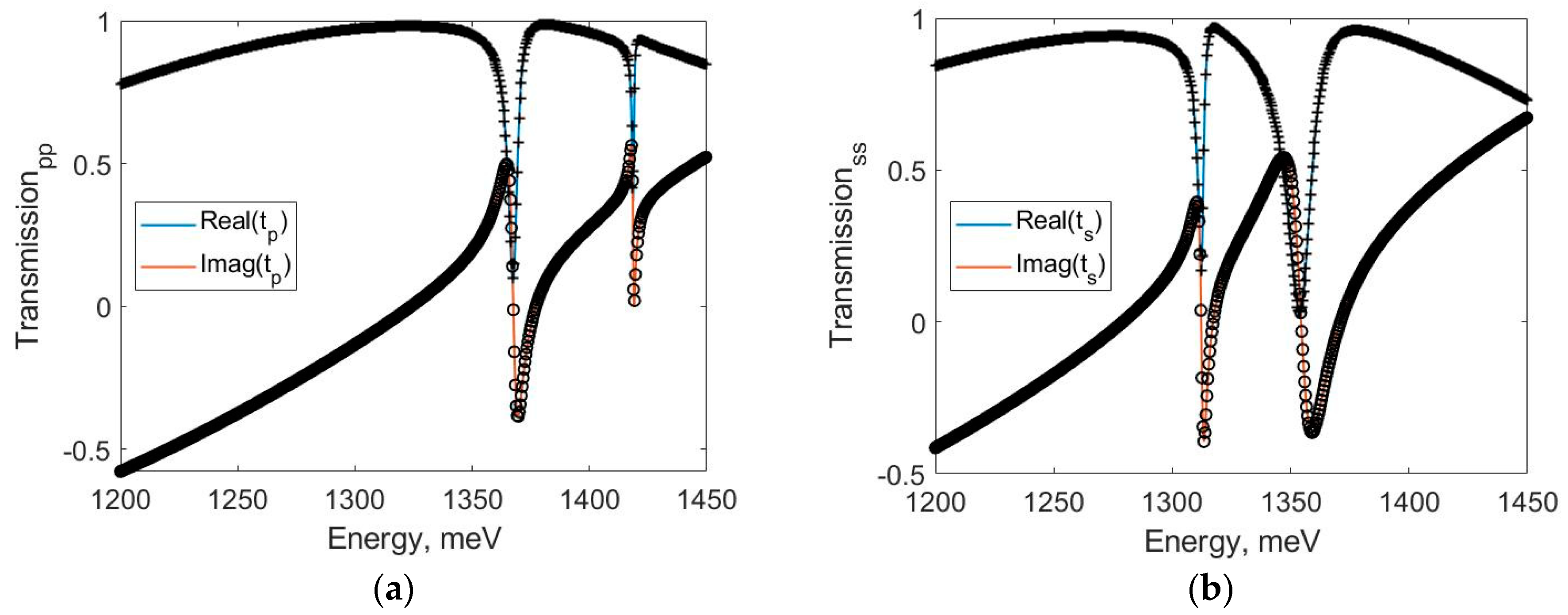
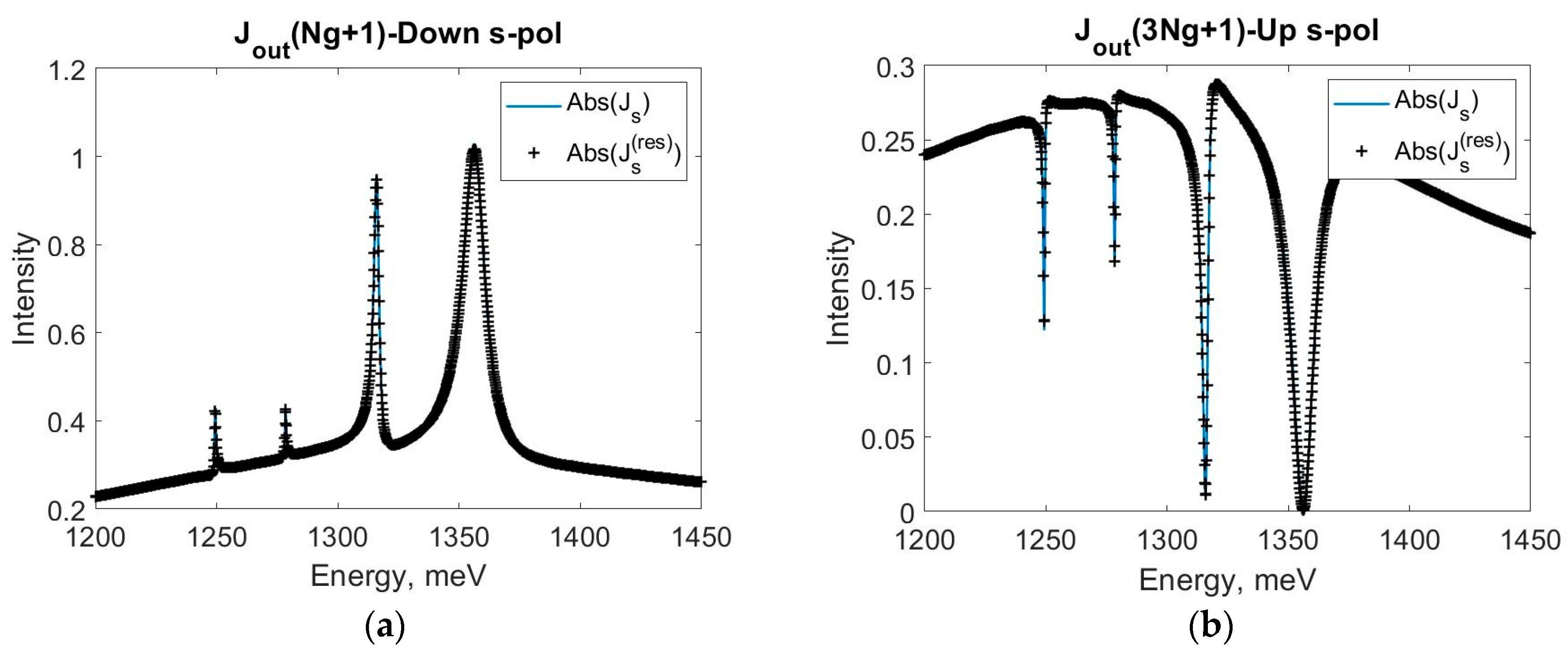
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Lalanne, P.; Yan, W.; Vynck, K.; Sauvan, C.; Hugonin, J. Light interaction with photonic and plasmonic resonances. Laser Photonics Rev. 2018, 12, 1700113. [Google Scholar] [CrossRef]
- Tikhodeev, S.; Yablonskii, A.; Muljarov, E.; Gippius, N.; Ishihara, T. Quasiguided modes and optical properties of photonic crystal slabs. Phys. Rev. B 2002, 66, 045102. [Google Scholar] [CrossRef]
- Gippius, N.; Tikhodeev, S.; Ishihara, T. Optical properties of photonic crystal slabs with an asymmetrical unit cell. Phys. Rev. B 2005, 72, 045138. [Google Scholar] [CrossRef]
- Gippius, N.; Weiss, T.; Tikhodeev, S.; Giessen, H. Resonant mode coupling of optical resonances in stacked nanostructures. Opt. Express 2010, 18, 7569–7574. [Google Scholar] [CrossRef] [PubMed]
- Fradkin, I.; Dyakov, S.; Gippius, N. Fourier modal method for the description of nanoparticle lattices in the dipole approximation. Phys. Rev. B 2019, 99, 075310. [Google Scholar] [CrossRef]
- Muljarov, E.; Langbein, W.; Zimmermann, R. Brillouin-Wigner perturbation theory in open electromagnetic systems. Europhys. Lett. 2010, 92, 50010. [Google Scholar] [CrossRef]
- Weiss, T.; Schäferling, M.; Giessen, H.; Gippius, N.; Tikhodeev, S.; Langbein, W.; Muljarov, E. Analytical normalization of resonant states in photonic crystal slabs and periodic arrays of nanoantennas at oblique incidence. Phys. Rev. B 2017, 96, 045129. [Google Scholar] [CrossRef]
- Whittaker, D.; Culshaw, I. Scattering-matrix treatment of patterned multilayer photonic structures. Phys. Rev. B 1999, 60, 2610–2618. [Google Scholar] [CrossRef]
- Lobanov, S.; Weiss, T.; Dregely, D.; Giessen, H.; Gippius, N.; Tikhodeev, S. Emission properties of an oscillating point dipole from a gold Yagi-Uda nanoantenna array. Phys. Rev. B 2012, 85, 155137. [Google Scholar] [CrossRef]
- Weiss, T.; Gippius, N.; Granet, G.; Tikhodeev, S.; Taubert, R.; Fu, L.; Schweizer, H.; Giessen, H. Strong Resonant mode coupling of Fabry–Perot and grating resonances in stacked two-layer systems. Photonics Nanostruct. Fundam. Appl. 2011, 9, 390–397. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gromyko, D.; Fradkin, I.; Dyakov, S.; Gippius, N. Resonant Mode Coupling Method for the Description of Oscillating Dipoles Emission inside Stacked Photonic Nanostructures. Mater. Proc. 2021, 4, 34. https://doi.org/10.3390/IOCN2020-07928
Gromyko D, Fradkin I, Dyakov S, Gippius N. Resonant Mode Coupling Method for the Description of Oscillating Dipoles Emission inside Stacked Photonic Nanostructures. Materials Proceedings. 2021; 4(1):34. https://doi.org/10.3390/IOCN2020-07928
Chicago/Turabian StyleGromyko, Dmitrii, Ilia Fradkin, Sergey Dyakov, and Nikolay Gippius. 2021. "Resonant Mode Coupling Method for the Description of Oscillating Dipoles Emission inside Stacked Photonic Nanostructures" Materials Proceedings 4, no. 1: 34. https://doi.org/10.3390/IOCN2020-07928
APA StyleGromyko, D., Fradkin, I., Dyakov, S., & Gippius, N. (2021). Resonant Mode Coupling Method for the Description of Oscillating Dipoles Emission inside Stacked Photonic Nanostructures. Materials Proceedings, 4(1), 34. https://doi.org/10.3390/IOCN2020-07928




