Asymmetric Hysteresis Loops and Horizontal Loop Shifts in Purely Ferromagnetic Nanoparticles †
Abstract
:1. Introduction
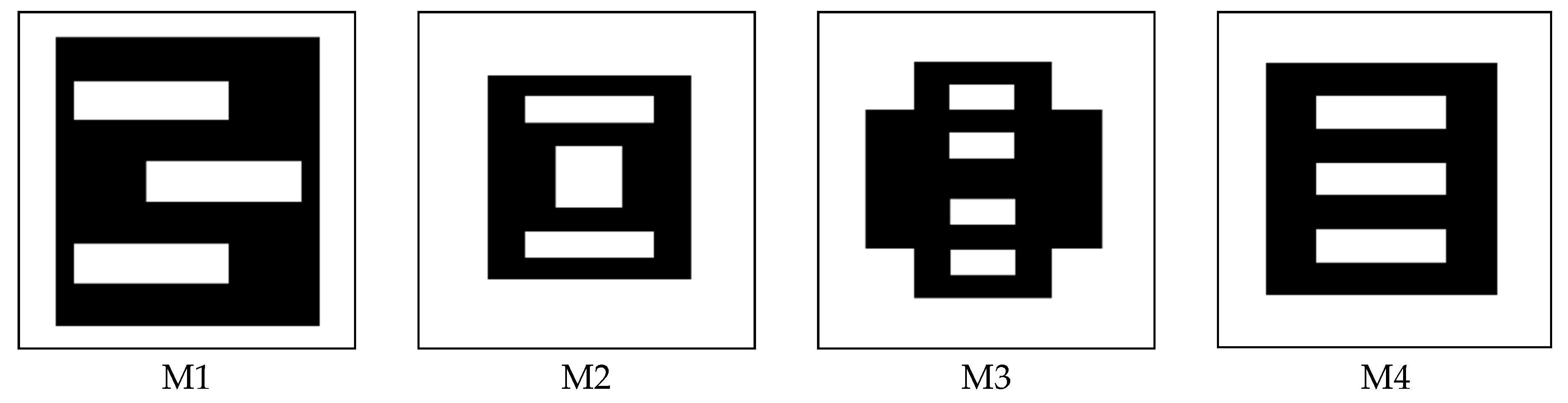
2. Materials and Methods
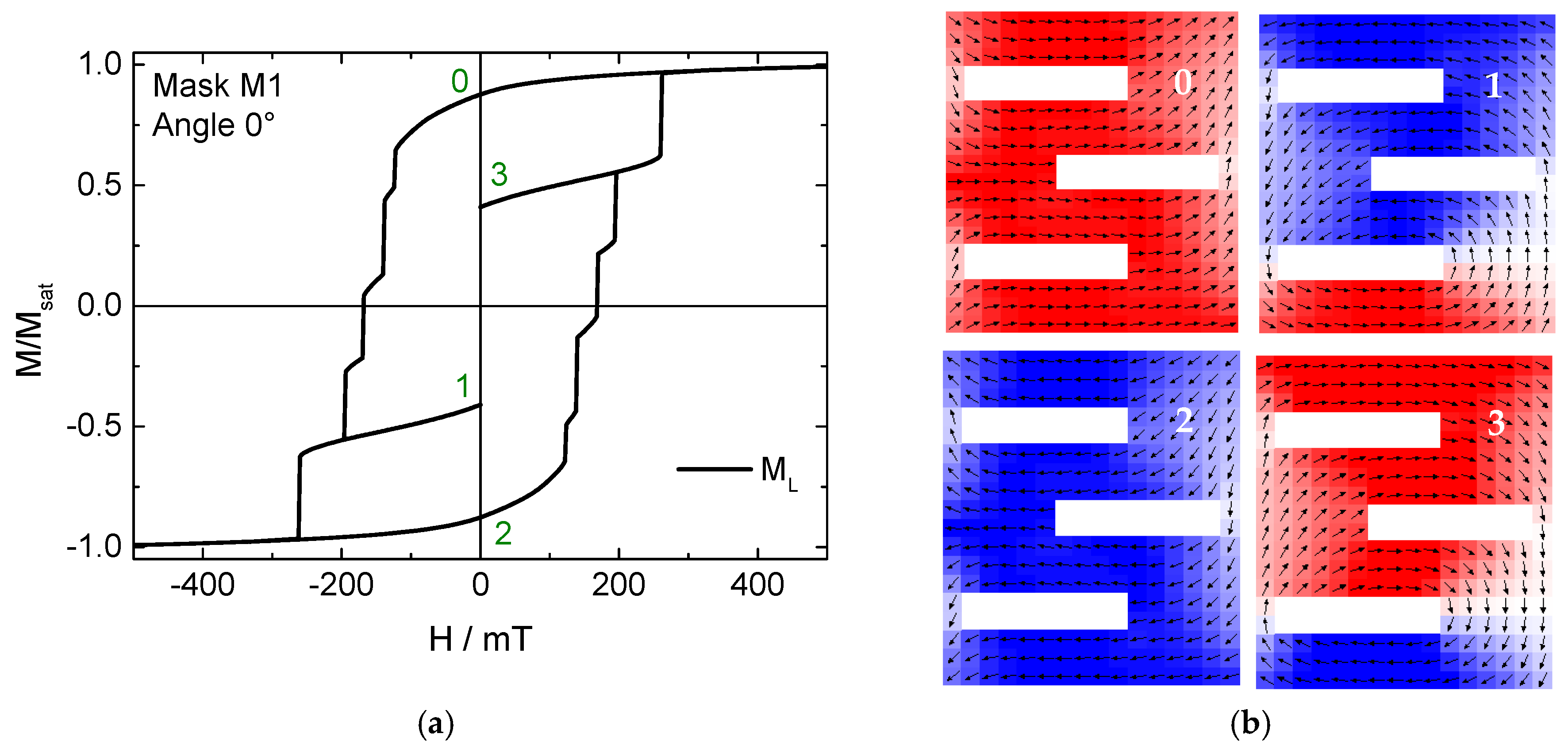
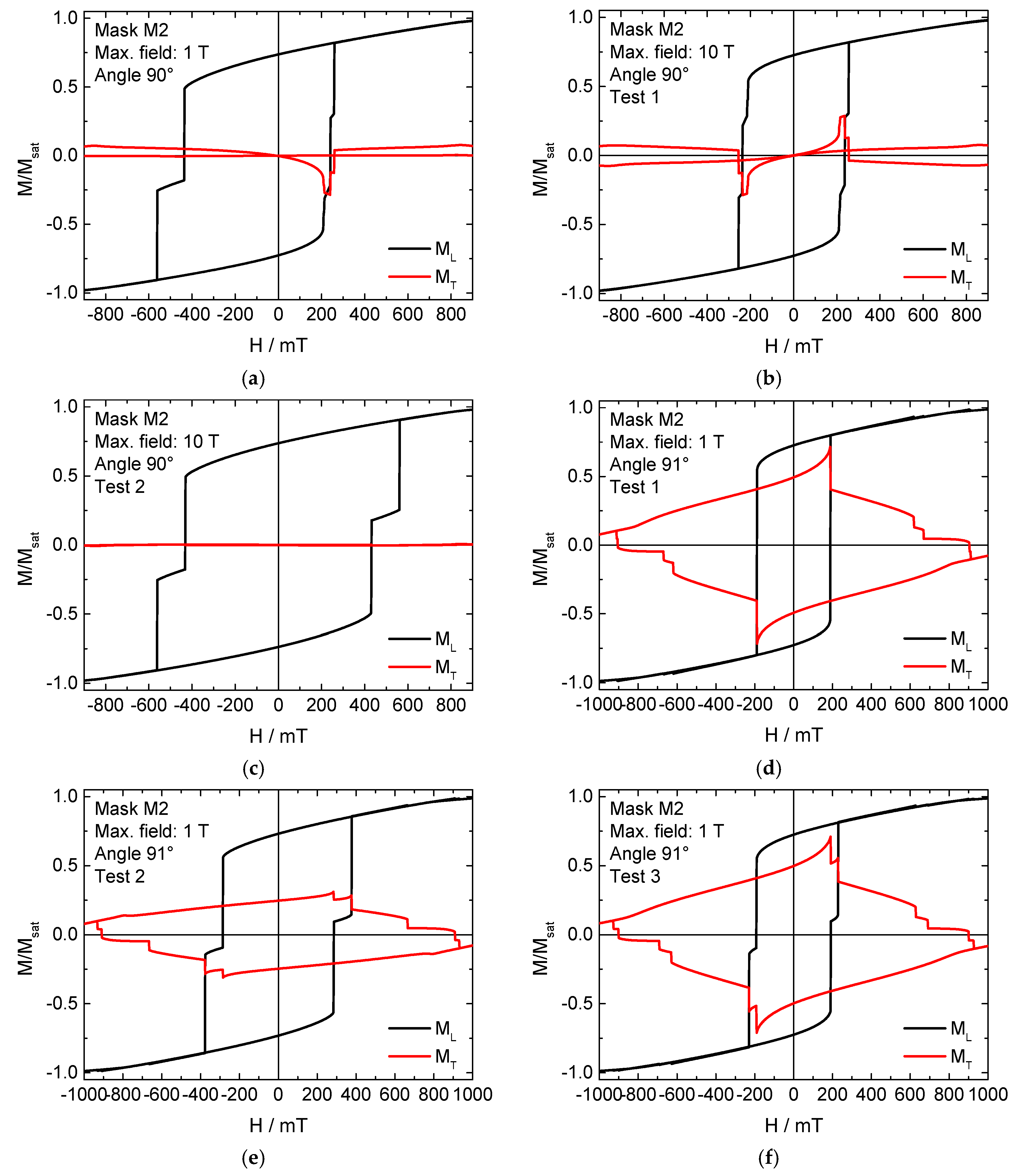
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morales, T.; Basaran, A.C.; Villegas, J.E.; Navas, D.; Soriano, N.; Mora, B.; Redondo, C.; Batlle, X.; Schuller, I.K. Exchange-Bias Phenomenon: The Role of the Ferromagnetic Spin Structure. Phys. Rev. Lett. 2015, 114, 097202. [Google Scholar] [CrossRef] [PubMed]
- Meiklejohn, W.P.; Bean, C.P. New magnetic anisotropy. Phys. Rev. 1956, 102, 1413. [Google Scholar] [CrossRef]
- Koon, N.C. Calculations of exchange bias in thin films with ferromagnetic/antiferromagnetic interfaces. Phys. Rev. Lett. 1997, 78, 4865. [Google Scholar] [CrossRef]
- Blachowicz, T.; Tillmanns, A.; Fraune, M.; Ghadimi, R.; Beschoten, B.; Güntherodt, G. Exchange bias in epitaxial CoO/Co bilayers with different crystallographic symmetries. Phys. Rev. B 2007, 75, 054425. [Google Scholar] [CrossRef]
- O’Grady, K.; Fernancez-Outon, L.E.; Vallejo-Fernandez, G. A new paradigm for exchange bias in polycrystalline thin films. J. Magn. Magn. Mater. 2010, 322, 883–899. [Google Scholar] [CrossRef]
- Ehrmann, A.; Blachowicz, B. Angle and rotational direction dependent horizontal loop shift in epitaxial Co/CoO bilayers on MgO(100). AIP Adv. 2017, 7, 115223. [Google Scholar] [CrossRef]
- Parkin, S.; Jiang, X.; Kaiser, C.; Panchula, A.; Roche, K.; Samant, M. Magnetically engineered spintronic sensors and memory. Proc. IEEE 2003, 91, 661–680. [Google Scholar] [CrossRef]
- Anh Nguyen, T.N.; Fang, Y.; Fallahi, V.; Benatmane, N.; Mohseni, S.M.; Dumas, R.K.; Akerman, J. [Co/Pd]–NiFe exchange springs with tunable magnetization tilt angle. Appl. Phys. Lett. 2011, 98, 172502. [Google Scholar] [CrossRef]
- Bonfirm, M.; Ghiringhelli, G.; Montaigne, F.; Pizzini, S.; Brookes, N.B.; Petroff, F.; Vogel, J.; Camarero, J.; Fontaine, A. Element-selective nanosecond magnetization dynamics in magnetic heterostructures. Phys. Rev. Lett. 2001, 86, 3646. [Google Scholar] [CrossRef]
- Gasi, T.; Nayak, A.K.; Winterlik, J.; Ksenofontov, V.; Adler, P.; Nicklas, M.; Felser, C. Exchange-spring like magnetic behavior of the tetragonal Heusler compound Mn2FeGa as a candidate for spin-transfer torque. Appl. Phys. Lett. 2013, 102, 202402. [Google Scholar] [CrossRef]
- Meiklejohn, W.H. Exchange anisotropy—A review. J. Appl. Phys. 1962, 33, 1328. [Google Scholar] [CrossRef]
- Nogués, J.; Schuller, I.K. Exchange bias. J. Magn. Magn. Mater. 1999, 192, 203–232. [Google Scholar] [CrossRef]
- Beschoten, B.; Keller, J.; Tillmanns, A.; Güntherodt, G. Domain state model for exchange bias: Training effect of diluted Co1-yO on exchange bias in Co-CoO. IEEE Trans. Magn. 2002, 38, 2744–2746. [Google Scholar] [CrossRef]
- Morales, R.; Li, Z.-P.; Olamit, J.; Liu, K.; Alameda, J.M.; Schuller, I.K. Role of the antiferromagnetic Bulk spin structure on exchange bias. Phys. Rev. Lett. 2009, 102, 097201. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.Y.; Wu, C.-B.; Kuch, W. Pinned magnetic moments in exchange bias: Role of the antiferromagnetic bulk spin structure. Phys. Rev. B 2014, 89, 094427. [Google Scholar] [CrossRef]
- Ehrmann, A.; Komraus, S.; Blachowicz, T.; Domino, K.; Nees, M.K.; Jakobs, P.J.; Leiste, H.; Mathes, M.; Schaarschmidt, M. Pseudo exchange bias due to rotational anisotropy. J. Magn. Magn. Mater. 2016, 412, 7–10. [Google Scholar] [CrossRef]
- Henne, B.; Ney, V.; de Souza, M.; Ney, A. Exchange-bias-like effect of an uncompensated antiferromagnet. Phys. Rev. B 2016, 93, 144406. [Google Scholar] [CrossRef]
- Yoo, T.H.; Khym, S.; Yea, S.-Y.; Lee, S.H.; Liu, X.; Furdyna, J.K. Four discrete Hall resistance states in single-layer Fe film for quaternary memory devices. Appl. Phys. Lett. 2009, 95, 202505. [Google Scholar] [CrossRef]
- Donahue, M.J.; Porter, D.G. OOMMF User’s Guide, Version 1.0; Interagency Report NISTIR 6376; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1999. [Google Scholar]
- Gilbert, T.L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 2004, 40, 3443. [Google Scholar] [CrossRef]
- Sudsom, D.; Juhász Junger, I.; Döpke, C.; Blachowicz, T.; Hahn, L.; Ehrmann, A. Micromagnetic simulation of vortex development in magnetic bi-material bow-tie structures. Cond. Matter 2020, 5, 5. [Google Scholar] [CrossRef]
- Cowburn, R.P.; Adeyeye, A.O.; Welland, M.E. Configurational anisotropy in nanomagnets. Phys. Rev. Lett. 1998, 81, 5414. [Google Scholar] [CrossRef]
- Tillmanns, A.; Oertker, S.; Beschoten, B.; Güntherodt, G.; Leighton, C.; Schuller, I.K.; Nogués, J. Magneto-optical study of magnetization reversal asymmetry in exchange bias. Appl. Phys. Lett. 2006, 89, 202512. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Detzmeier, J.; Königer, K.; Ehrmann, A. Asymmetric Hysteresis Loops and Horizontal Loop Shifts in Purely Ferromagnetic Nanoparticles. Mater. Proc. 2021, 4, 13. https://doi.org/10.3390/IOCN2020-07836
Detzmeier J, Königer K, Ehrmann A. Asymmetric Hysteresis Loops and Horizontal Loop Shifts in Purely Ferromagnetic Nanoparticles. Materials Proceedings. 2021; 4(1):13. https://doi.org/10.3390/IOCN2020-07836
Chicago/Turabian StyleDetzmeier, Joscha, Kevin Königer, and Andrea Ehrmann. 2021. "Asymmetric Hysteresis Loops and Horizontal Loop Shifts in Purely Ferromagnetic Nanoparticles" Materials Proceedings 4, no. 1: 13. https://doi.org/10.3390/IOCN2020-07836
APA StyleDetzmeier, J., Königer, K., & Ehrmann, A. (2021). Asymmetric Hysteresis Loops and Horizontal Loop Shifts in Purely Ferromagnetic Nanoparticles. Materials Proceedings, 4(1), 13. https://doi.org/10.3390/IOCN2020-07836






