Prediction of the Magnetocaloric Effect of Ni₄₂Mn₄₆CoSn₁₁ Heusler Alloy with a Phenomenological Model ^†

Abstract

Intermetallic NiMn-based Heusler alloys (HAs) have garnered considerable attention due to their multifunctionality and applications in various fields, including sensors, actuation, refrigeration, and waste heat harvesters. Among the NiMn-based alloys, Ni-Mn-Sn alloys have gained considerable attention since their structural and magnetic transformations were discovered. Many studies have been conducted with various compositions and shapes to investigate the physical properties of Ni-Mn-Sn alloys, which offer several advantages, including non-toxicity, low cost, and abundant constituents. The Co-doping effect on the physical properties of Ni-Mn-Sn alloys has been widely reported. This doping can rectify the ternary Ni-Mn-Sn Heusler compound’s brittleness by crystallizing a disordered face-centered cubic (fcc) γ-phase. In this study, a polycrystalline Ni₄₂Mn₄₆CoSn₁₁ Heusler alloy was prepared by high-frequency fusion (HF), using a Lin Therm 600 device, from pure Ni, Mn, Sn, and Co elements with appropriate proportions. X-ray diffraction, scanning electron microscopy, and magnetic magnetometry devices were used to study the structural, microstructural, and magnetic properties. The XRD results revealed the coexistence of a disordered 7 M martensite phase (~88%) and a disordered cubic solid solution γ-phase (~12%). The alloy underwent a second-order ferromagnetic-to-paramagnetic phase transition at a Curie temperature of 350 K. Landau and Hamad’s theoretical models were used to plot the magnetic entropy change. The magnetocaloric properties (the maximum entropy change value, ΔS_M, the full width at half maximum of the entropy change curve, δT_FWHM, the relative cooling power, RCP, and the heat capacity, ΔC_P,H) were calculated using isothermal magnetization curves with the phenomenological model of Hamad.

1. Introduction

Since structural and magnetic transformation have been reported in Ni-Mn-Z (Z = Ga, Sn, In) alloys [1], many studies on austenitic and martensitic states have been investigated [2,3,4,5,6]. Upon cooling, these alloys undergo a first-order martensitic transition from a high-temperature-modulated or non-modulated martensite phase with complex magnetic behavior. The magnetization is smaller in the martensite phase than in the austenite phase, and magnetic coupling is ferromagnetic in the high-temperature phase and is short-range antiferromagnetic for Mn-rich compounds [7,8]. Also, the magnetic properties are dominated by Mn-Mn coupling in stoichiometric compositions of Ni₂MnZ. However, ferromagnetic/antiferromagnetic interactions have been found in the off-stoichiometric ones, in which Mn atoms occupying Z sites coupled antiferromagnetically to Mn in their own regular sites. One can observe an important magnetocaloric effect near the first-order magneto-structural transition [9]. However, in the vicinity of the second-order magnetic transition, a magnetocaloric moderate impact exists. Ternary alloys of Ni-Mn-Sn compounds are of great interest, owing to their various properties and applications [10,11,12,13]. Substituting a Ni, Mn, or Sn site with a fourth element modifies its structural transformation and magnetic properties, such as the saturation magnetization and magnetic entropy change [14,15]. Furthermore, fourth-element doping in Ni-Mn-Sn alloys improves their ductility by γ-phase formation.

The aim of this study is to model magnetic entropy change by using Landau and Hamad’s theories and to predict the magnetocaloric properties based on Hamad’s theoretical model [16].

2. Materials and Methods

The intermetallic Ni₄₂Mn₄₆CoSn₁₁ Heusler alloy was prepared by high-frequency fusion (HF), using a Lin Therm 600 device, from pure Ni, Mn, Sn, and Co elements with appropriate proportions. X-ray diffraction (BRUCKER D8 Discover diffractometer, Bruker AXS GmbH, Karlsruhe, Germany), scanning electron microscopy (FEI Quantum 250, FEI Company, Hillsboro, OR, USA), and magnetic magnetometry (BS2) devices were used to study the structural, microstructural, and magnetic properties. The prediction of the magnetocaloric properties based on the theoretical model of Hamad has been determined from the magnetization measurement M(T).

3. Results

3.1. Structure and Microstructure

Figure 1 shows the Rietveld refinement of the polycrystalline Ni₄₂Mn₄₆CoSn₁₁ Heusler alloy using the MAUD program [17] (version 2.94). The XRD pattern reveals that the alloy structure consists of a mixture of disordered phases, including 7 M modulated martensite (space group P2/m, volume fraction 88%, lattice parameters a = 4.342 Å, b = 5.665 Å, and c = 29.223 Å) with a monoclinicity angle of β = 92.87°, and fcc γ-phase (space group Fm-3m, volume fraction 12%, lattice parameter a = 3.605 Å).

The SEM micrograph (Figure 2) consists of dendritic and lamellar microstructures that grow in a bright matrix and dark γ-phase.

3.2. Magnetocaloric Effect Modeling: Landau Theory

Amaral et al. [18] proposed a model for magnetic entropy based on Landau’s theory [19]. This model takes into account magnetoelastic contributions and interactions between electrons in a magnetic system. The authors assumed that the thermodynamic potential (e.g., the free enthalpy G) can be expanded as a function of powers of the order parameters, namely using the magnetization M. When the magnetization of a ferromagnetic system is small, its free energy, which is near the Curie temperature, can be expanded to a power of M according to the following relationship:

G(M,T) = G₀ + a₁(T)M + a₂(T)M²/2 + a₃(T)M³/3 + a₄(T)M⁴/4 + …… − HM

(1)

For reasons of symmetry, the configuration M and −M must give the same free energy, hence the disappearance of the terms of odd order. By neglecting the terms whose powers are very high, the free energy as a function of the total magnetization can be developed as follows:

G(M,T) = G₀ + a(T)M²/2 + b(T)M⁴/4 + c(T)M⁶/6 + …… − HM

(2)

For an equilibrium condition, δG/δM = 0, the equation which describes the total magnetization in the vicinity of the Curie temperature is given by

H = a(T)M + b(T)M³ + c(T)M⁵

(3)

where the coefficients a(T), b(T), and c(T) are the Landau parameters. From Figure 3b, one can notice that a(T) is positive and has a minimum at the Curie temperature (T_C = 350 K). For T = T_C, b(T) is positive, indicating that the magnetic transition is of the second order. Accordingly, the theoretical model of magnetic entropy change is given by means of a derivative of the free energy with respect to temperature, written in the following relation:

−ΔS_M(T,H) = a’(T)M²/2 + b’(T)M⁴/4 + c’(T)M⁶/6

(4)

where a’(T), b’(T), and c’(T) are the derivatives of Landau’s coefficient with respect to temperature. The plots of the numeric calculation of −ΔS_M are depicted in Figure 3a, which mentions that −ΔS_M reaches 0.95 J/kgK under an applied magnetic field of 5 T.

3.3. Prediction of Magnetocaloric Effect: Phenomenological Model

Based on Hamad’s model [16], the dependence of the magnetization can be written as a function of the temperature and the Curie temperature as follows:

M(T,H) = [(M_i − M_f)/2] tanh [A × (T_C − T)] + (B × T) + C

(5)

where M_i and M_f are the corresponding initial and final values of magnetization at ferromagnetic/paramagnetic phase transition, respectively. The coefficients B (the magnetization sensitivity, dM/dT, in the ferromagnetic region before the transition), C, and A are defined by the following relations:

B = (dM/dT)_{T ≈ Ti}

(6)

C = [(M_i + M_f)/2] − (B × T_C)

(7)

A = 2 × (B − S_C)/(Mi − Mf)

(8)

S_C is the magnetization sensitivity at Curie temperature. The magnetic entropy change under an adiabatic magnetic field variation from 0 to 5 T can be evaluated through the following equation:

ΔS_M = H × [−A ((M_i − M_f)/2) sech² (A × (T_C − T)) + B]

(9)

The maximum magnetic entropy change, ΔS_M,max, obtained at T = T_C is given by

ΔS_M,max = H * [−A ((M_i − M_f)/2) + B]

(10)

The full width at half maximum, δT_FWHM, is calculated as follows:

δT_FWHM = (2/A) sech [([2A × (M_i − M_f)]/[A × (M_i − M_f) + 2B])^1/2]

(11)

The relative cooling power, RCP, which corresponds to the quantity of the heat transferred from the hot source to the cold one, is estimated using the given relation:

RCP = −δT_FWHM × ΔS_M,max = H × [ M_i − M_f − 2B/A] sech [([2A * (M_i − M_f)]/[A × (M_i − M_f) + 2B])^1/2]

(12)

The specific heat change, ΔC_P,H, can be calculated from the contribution to the entropy change induced in the material and is given by

ΔC_P,H = H × T × A² (M_i − M_f) sech² tanh [A × (T_C − T)] sech² [A × (T_C − T)]

(13)

To apply the proposed model, numerical calculations were carried out with the different parameters listed in

Table 1. Model parameters of the initial and final values of magnetization (M_i and M_f, respectively) at Curie temperature (T_C), a well as coefficients A and B and the magnetization sensitivity (S_C) for different applied magnetic fields.

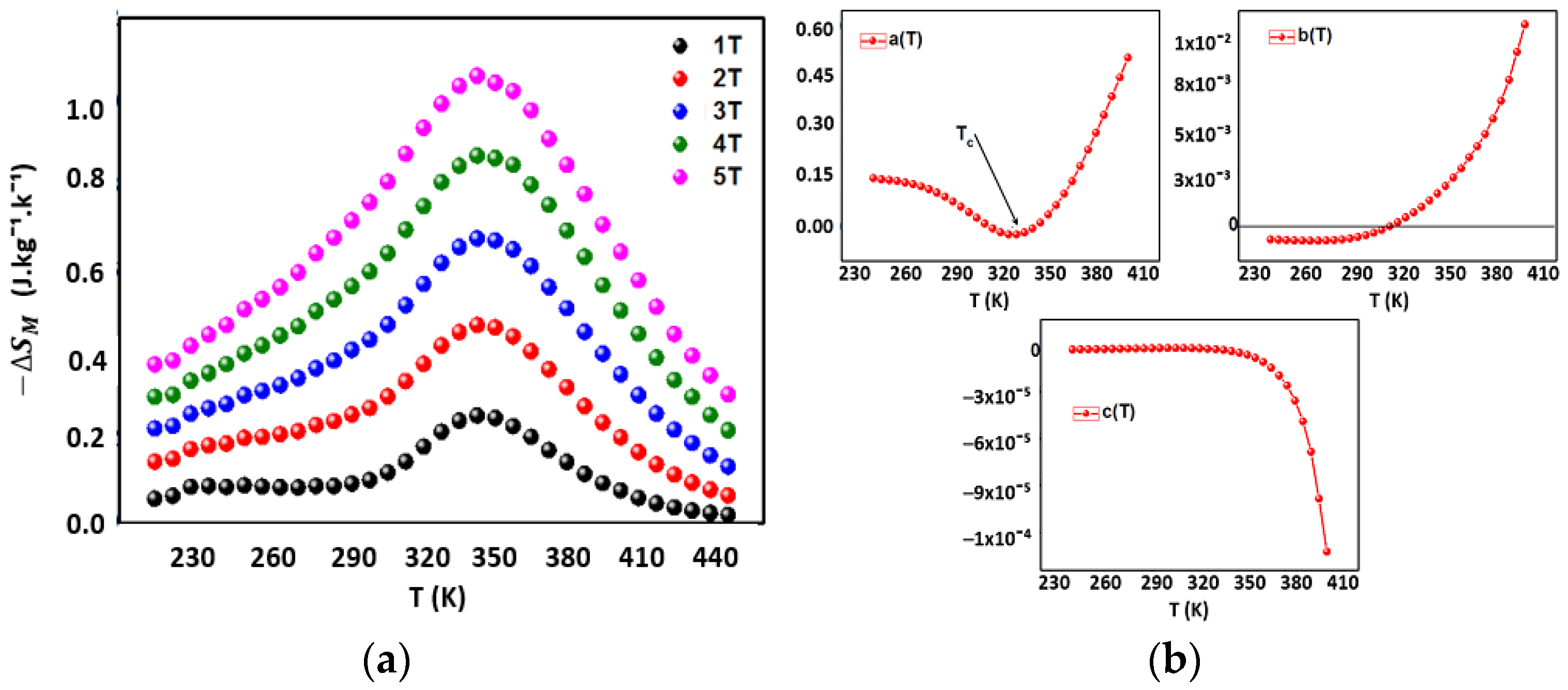
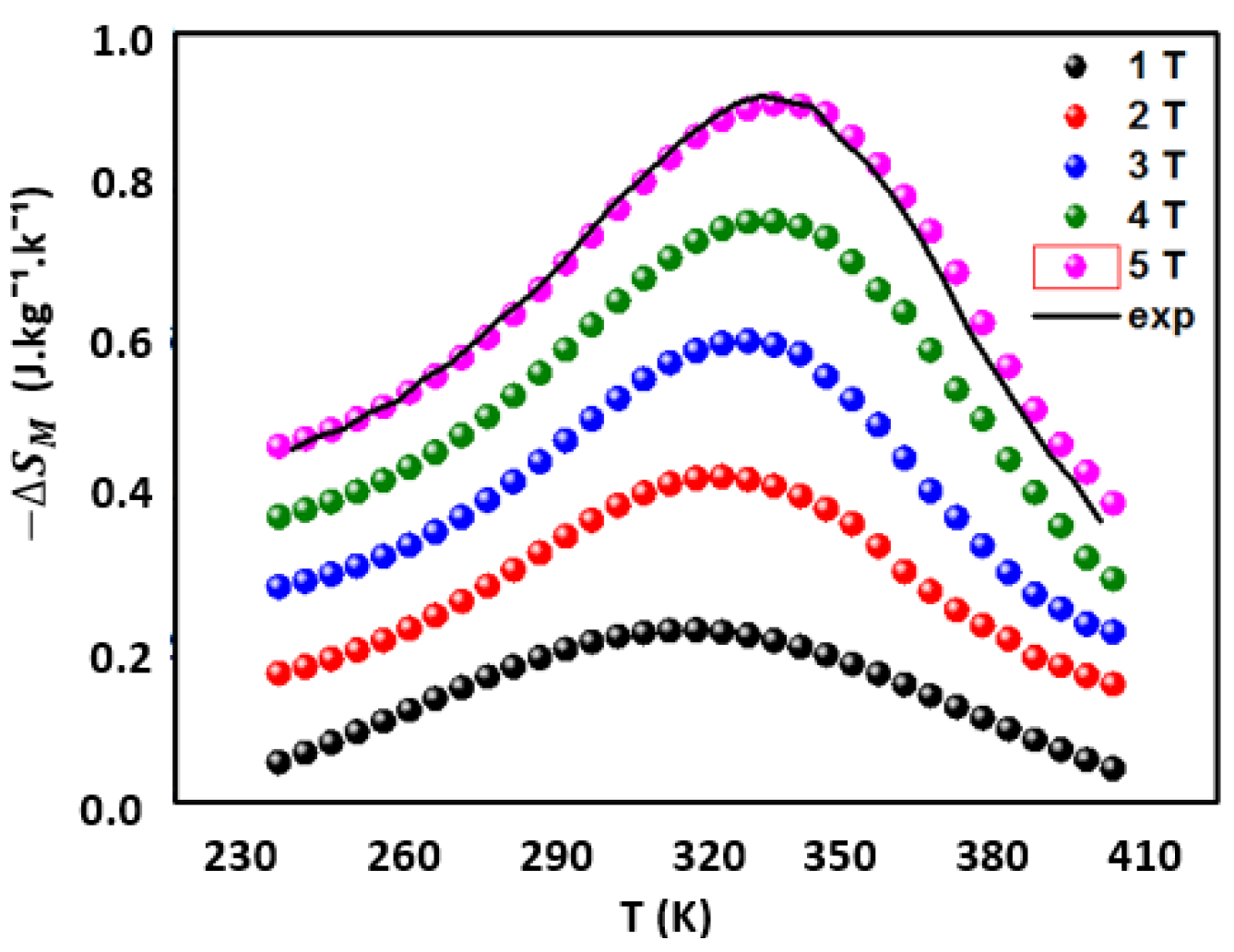
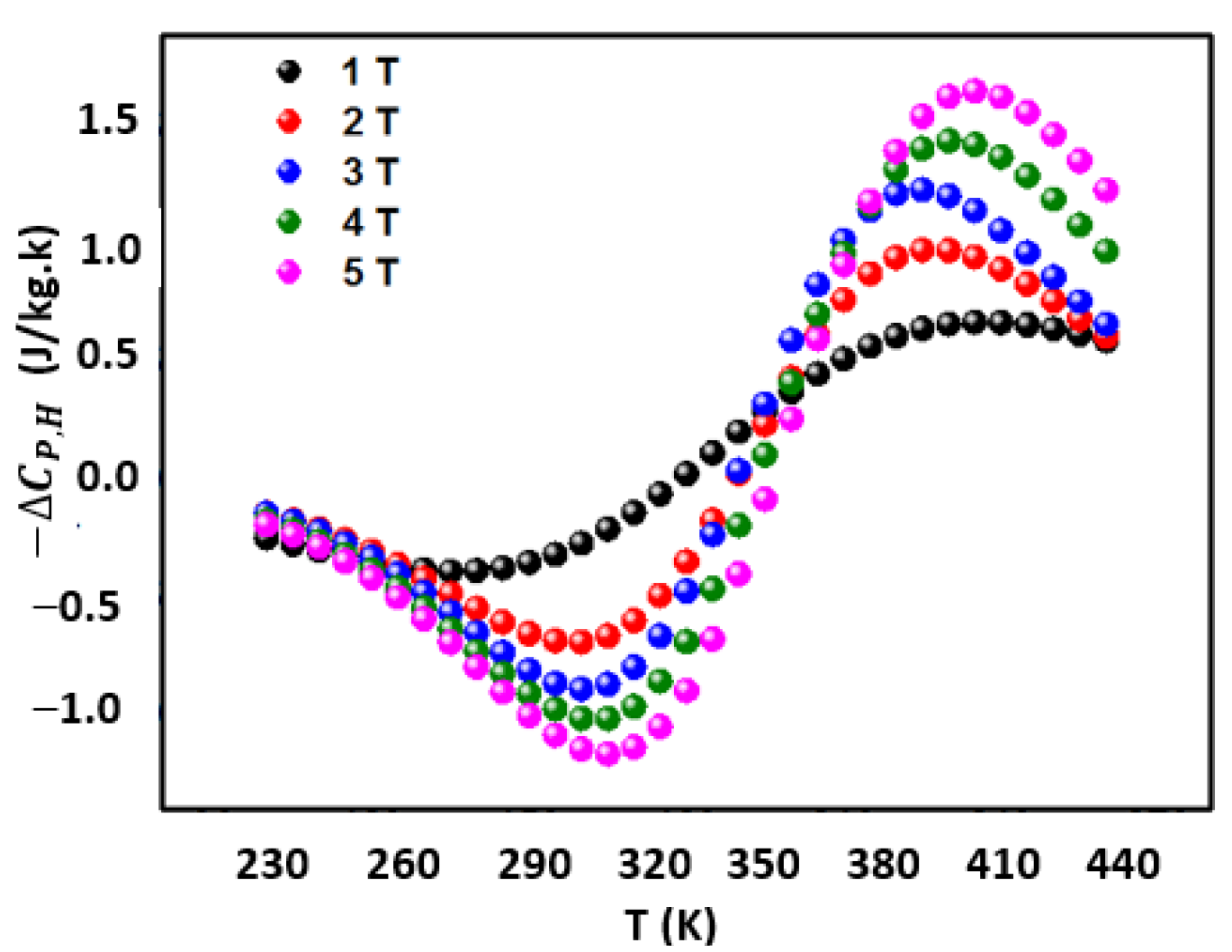
µ0H (T)	Mi (emu/g)	Mf (emu/g)	TC (K)	A (K−1)	B (emu/gK)	SC (emu/gK)
1	37.5536	1.0520	331.07	0.0131	−0.0482	−0.2198
2	25.3502	7.8995	339.18	0.0190	−0.0622	−0.2091
3	22.9066	11.0964	343.86	0.0216	−0.0823	−0.1978
4	23.0751	12.3441	347.91	0.0195	−0.0817	−0.1859
5	24.4584	12.6313	350.20	0.0189	−0.0828	−0.1792

. Figure 4 represents the variation curves of the magnetization M as a function of the temperature at different applied magnetic fields. The experimental data (symbols) have been fitted by Equation (5) (red solid line). We can notice that this equation more or less describes the shape of magnetization, hence the validity of this model.

The experimental results of the magnetic entropy change variation and the simulated curves (solid line) are depicted in Figure 5. It is clear that the calculated results from Equation (9) are in good agreement with the experimental data. This affirms that this model correctly describes the behavior of magnetization over a wide range of temperatures, including the phase transition region, regardless of the external magnetic field. The predicted magnetocaloric properties such as the maximum entropy change value, the full width at half maximum of the entropy change, the relative cooling power, and the heat capacity are calculated and tabulated in

Table 2. Predicted values of the magnetocaloric properties such as the maximum entropy change (ΔS_M,max), the full width at half maximum of the entropy change (δT_FWHM), the relative cooling power (RCP), and the minimum and maximum heat capacity (ΔC_{P,H, min} and ΔC_{P,H, max}, respectively) for different applied magnetic fields.

µ0H (T)	ΔSM,max (J/kgK)	δTFWHM (K)	RCP (J/kg)	ΔCP,H, min (J/kgK)	ΔCP,H, max (J/kgK)
1	0.3051	36.6751	10.1840	−0.3779	0.6891
2	0.4536	34.3471	13.7305	−0.6768	0.9884
3	0.6603	63.2849	36.7886	−0.8548	1.2253
4	0.7967	92.3566	68.3692	−1.0371	1.4389
5	0.9689	156.5735	129.3906	−1.1753	1.6761

. The specific heat is positive before the magnetic temperature transition, negative after it, and deviates from zero only in the neighborhood (Figure 6). Furthermore, the minimum and maximum values of the heat capacity (ΔC_{P,H, min} and ΔC_{P,H, max}, respectively) increase as the applied magnetic field increases.

4. Conclusions

The polycrystalline Ni₄₂Mn₄₆CoSn₁₁ Heusler alloy exhibits both cubic γ and seven layered monoclinic structures, and it undergoes a second-order magnetic transition at a Curie temperature T_C = 350 K. Two theoretical models from Landau and Hamad were used to model the magnetic entropy change, which reached a value of about 0.95 J/kgK @5T. The magnetocaloric properties (the maximum entropy change value, ΔS_M,max, the full width at half maximum of the entropy change curve, δT_FWHM, the relative cooling power, RCP, and the heat capacity, ΔC_P,H) were calculated using M(T) curves with the phenomenological model of Hamad.