Numerical Modelling of Void Closure Diffusion Model ^†

Abstract

A void closure analytic model for the diffusion bonding of titanium TC4 alloy is developed in this study, in which an FEA-based deformation mechanism is coupled with a numerical analysis for diffusion. The focus was to evaluate the effect of pressure and the temperature on the bonded ratio. As the value of bonding pressure or the bonding temperature increased, the bonding time decreased. The dependence of bonded ratio and time was modeled as an exponential curve. The geometrical model for the mechanism was utilized so that it can incorporate the void division aspect in the process of diffusion bonding.

1. Introduction

Nickel-based superalloys exhibit unique mechanical properties at elevated temperatures due to the presence of different elements like Cr, Fe, and Nb and are widely used in industrial applications like the manufacturing of gas turbines, rockets, and aircrafts [1,2]. Commercially pure titanium has a high strength, and its corrosion resistance makes it suitable for biomedical, aerospace, and automobile applications [3,4]. The direct joining of titanium and nickel alloys often leads to the formation of intermetallic compounds, cracks, and the generation of residual stresses in the weldment [5]. A possible solution could be to alter the chemical composition of the weldment by incorporating an interlayer, thereby potentially improving the weld’s mechanical properties and reducing its susceptibility to cracking [6].

The initial development of a void closure model discussing plastic deformation, grain boundary diffusion, and power law creep diffusion was conducted by Cline et al. [7]. Hamilton et al. developed the interfacial void closure model for diffusion bonding and proposed that the initial stage of diffusion bonding is deformation of plastic surface [8]. Garmong et al. improved upon the model created by Hamilton and proposed that maximum void closure was achieved by a creep diffusion mechanism [9]. Derby et al. developed the first pressure-sintering model of diffusion bonding showing how the shape of the void changes from triangular to cylindrical [10]. Philling et al. developed the void closure model considering the effects of grain boundary diffusion and time-based creep diffusion [11]. Hill and Walloch developed the discontinuous computational model to achieve void closure, considering that surfaces consist of infinitely large numbers of cylinders that enable them to consider the elliptical cross section for the model [12]. They proposed different mechanisms of diffusion bonding, including the creep mechanism, surface source mechanism, and interface source mechanism. Li et al. developed the diffusion model for void closure to determine the bonding time required during the process. He utilized the stochastic characteristics for the surface finish, which involved creating a probabilistic model void by assuming the height and width of the void to be random [13]. Wu et al. developed the numerical model to calculate the bonded ratio and bonded time of the samples characterized by surface morphologies of long and short wavelengths based on actual surface morphology [14]. Yuan et al. proposed that void closure is basically characterized based on micro deformation at the interface [15]. Xydua et al. developed the molecular dynamics simulation to study the effect of pressure and temperature on voids formed between the grains [16]. Li et al. performed Spark Plasma Sintering (SPS) diffusion bonding to investigate the behavior of micro and nano voids. He carried out the molecular dynamic simulation for the same model [17].

Several researchers have used Finite Element Analysis (FEA) to model the diffusion bonding process. Takahashi et al. developed the FEA model for the diffusion bonding of copper which was free of oxygen to study the visco-plastic deformation observed during the process [18]. He later developed the meshed base void closure model and proposed that plastic deformation was dependent on the strain rate [19]. Alegria et al. developed the void closure model and discussed how pressure contributes to deformation in the early stages of diffusion bonding [20]. Wang developed the void closure model and considered the effects of pressure, temperature, time, and surface roughness on the initial stage of diffusion bonding for calculation of bonded ratio values [21]. Peng et al. added the creep diffusion mechanism to the diffusion bonding process and calculated the bonded ratio [22]. The creep expressions in the existing models were created for steady-state creep by Bird Mukherjee–Dorn (BMD) with the Sherby Dorn form of power law [23,24]. Rajakumar et al. studied the response of the surface to determine the optimum interface layer thickness to achieve maximum material parameters like shear strength and hardness [25]. Nagemiya et al. developed the experimental model for AISI304 and Ti-6Al-4V and developed graphical plots for P-t (bonding pressure and bonding time) and T-t (bonding temperature and bonding time) with the help of experimental values [26].

Previous studies have shown that diffusion bonding takes place between similar materials; that is why the authors of these studies consider one surface to be the master surface, showing no diffusion occurring on this side. In contrast, this study cannot model the diffusion of dissimilar joints. Thus, this study models diffusion on both sides of the mating surface so that this study can proceed to achieve successful bonding of dissimilar materials with voids shown in Figure 1. Moreover, the previous studies do not consider the phenomenon of void division which is carried out in our study.

2. Material and Methods

The void closure model has been established in the current study. This framework discusses how the voids closes in the materials, whether this occurs through surface diffusion or bulk diffusion, in order to understand the process parameters. The concept of selecting the voids on both the surfaces is established because of the nature of the voids that are actually present in the system after the surface has been polished. After looking under the AFM, we see that there are voids present on both the materials rather than on a single side.

The conceptual approach emphasizes the behavior of void closure, whether this takes the form of surface diffusion or bulk diffusion. The main factor that accounts for the diffusion process is the difference in the radius of curvature. This study also accounts for the diffusion based on the two main factors in this study, which are pressure and temperature, that greatly affect the bonding process. The closure of the voids is represented in Figure 2.

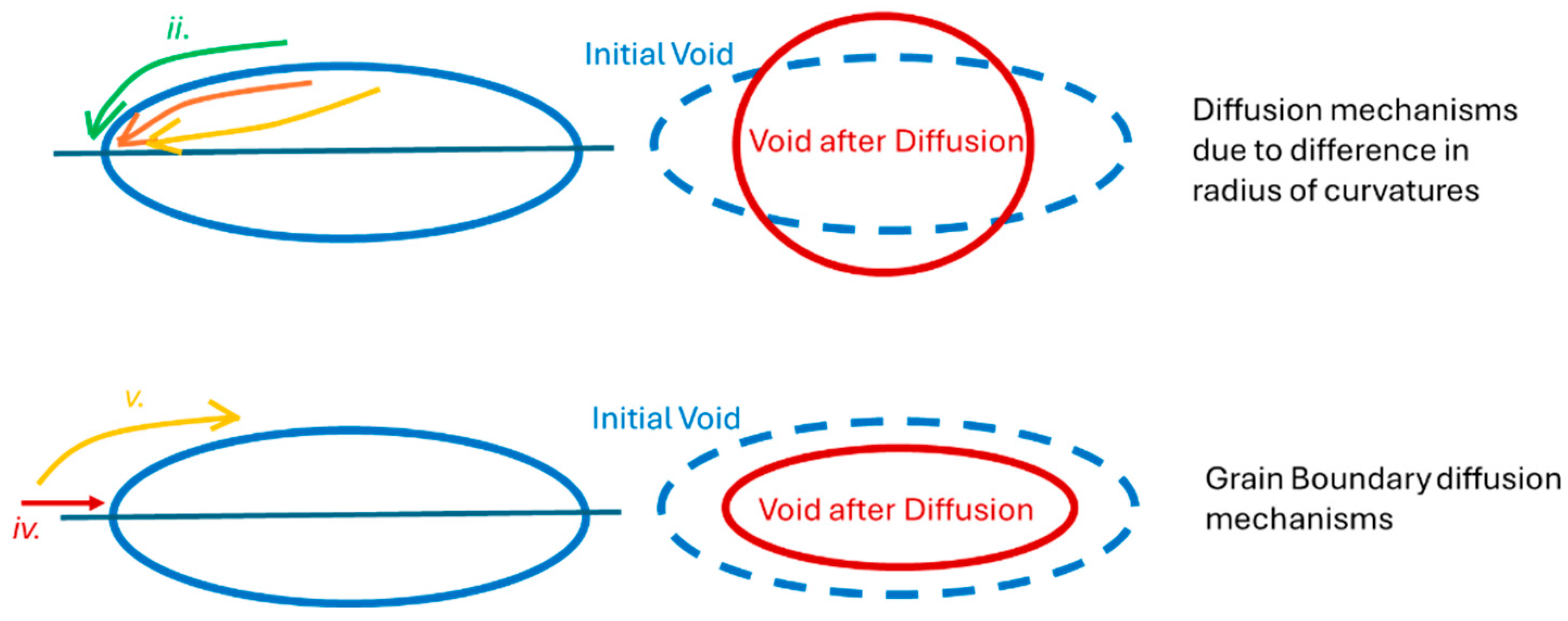
2.1. Geometric Modeling

The geometric CAD model for void closure model is developed to capture the intricate interaction at the interface between the two mating surfaces and the size of the void is determined with respect to the AFM conducted during experimentation. The CAD model for the void closure was developed using SOLIDWORKS version 2019. The main focus of this study was to discuss the division of the void so that the error between experimental and simulation due to this effect could be minimized. Thus, the CAD model considers two voids within a single void where there is a peak inside the void. In order to validate this experimentally, the size of the voids in simulation was taken same as the experimental AFM values. The geometric model of the void closure model is shown in Figure 3.

2.2. Mathematical Modeling

The simulated model of the current study is mated with the numerical model to develop the complete diffusion model. The model is developed to capture the effects of temperature, pressure, and bonding time and focuses on the extent to which the void is closed based on its bonded ratio. The Hill and Walloch model used in this study uses the elliptical void and develops the diffusion model using the numerical equations.

Key aspects of the mathematical model include the following:

• Diffusion coefficients that determine the rate of void closure.
• Pressure–temperature interactions that dictate the bonding process.
• Temporal variations in the closure dynamics which highlight the process efficiency.

The equations used to represent the mathematical model are as follows:

$$y-23.5=-0.0025{(x-63.5)}^2$$

(1)

$$\dot{V}={\displaystyle \frac{\partial V_{\mathrm{void}}}{\partial a}}\cdot \dot{a}+{\displaystyle \frac{\partial V_{\mathrm{void}}}{\partial h}}\cdot \dot{h}$$

(2)

$${\displaystyle \frac{\partial V_{\mathrm{void}}}{\partial a}}=-2\pi {\int }_0^{163.5}\left(23.5-a(x-65.4{)}^2\right)(x-65.4{)}^{2}dx$$

(3)

$${\displaystyle \frac{\partial V_{\mathrm{void}}}{\partial h}}=\pi {\int }_0^{163.5}{\displaystyle \frac{\partial }{\partial h}}\left[{\left(h-a(x-65.4{)}^2\right)}^2\right]dx$$

(4)

Here, y is the variable void height, x is the variable void width, $\dot{V}$ is the volume decrease rate of the void, $a$ is the void width, and h is the void height.

In Figure 4, the mathematical model for the parabola is shown where the x-axis show the void width and y-axis shows void height. During the void closure, the width and the height of the void change, so these are the variables that change from x to a and y to h, as represented in the above equations.

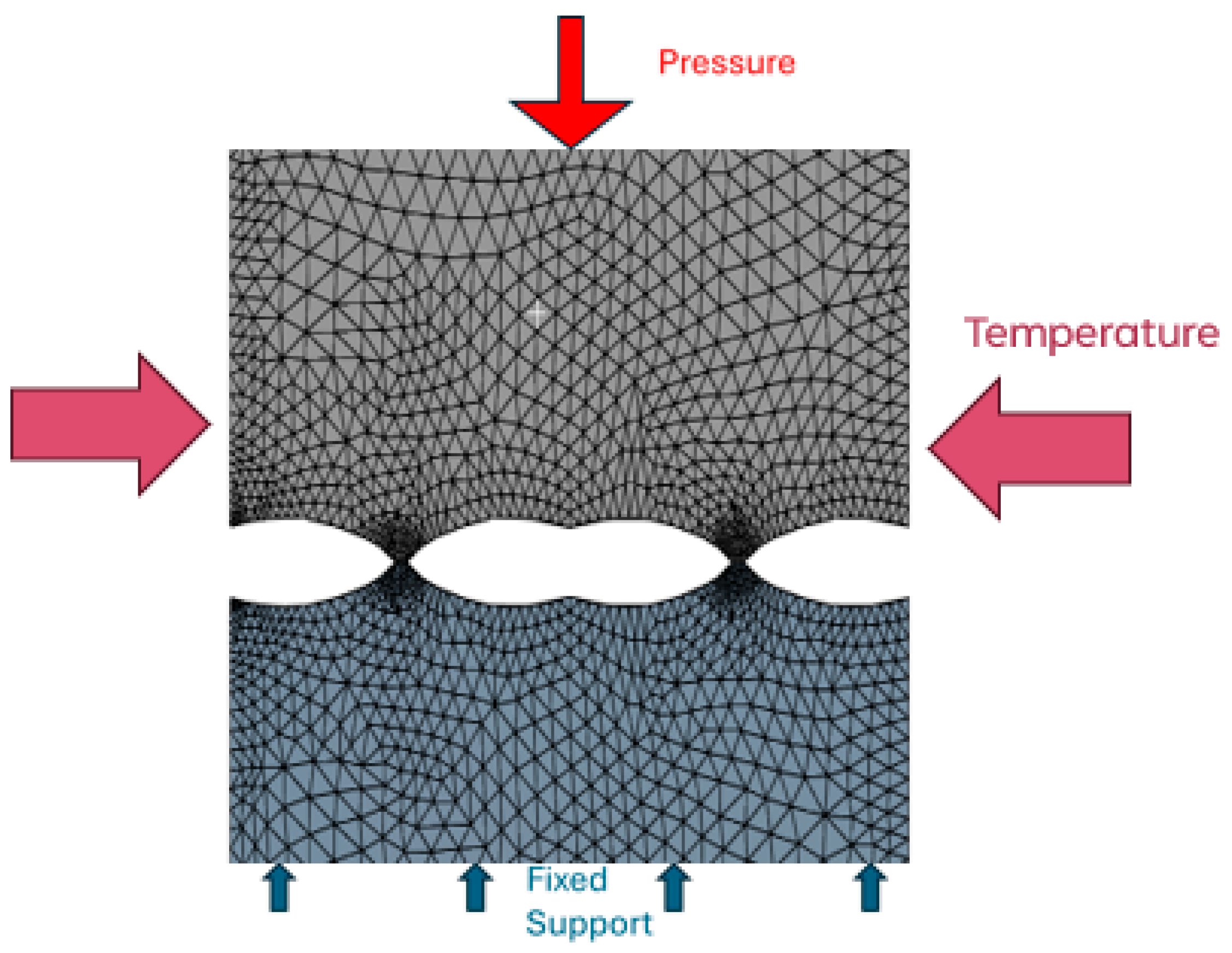
2.3. Meshing and Boundary Conditions

The mesh model and the boundary conditions are shown in Figure 5. It can be seen from the figure that the point of maximum deformations featured fine mesh and the coarse meshing was used elsewhere. The mesh model is shown in Figure 5. Fine meshing was adopted to capture the features of the deformation. The model had 450,760 (tet10) mesh elements. Firstly, the pressure was applied on the upper surface and the lower surface was kept fixed for the first second of the simulation. Then, a zero-displacement boundary condition was applied on both sides and temperature was applied for 3600 sec to study the creep behavior in the materials. The whole simulation was carried out in an ANSYS 2025 static structural module.

2.4. Simulation Parameters

Based on the experiments [27] conducted to study the diffusion bonding process, we selected the number of parameters in our current study. The main parameters in the study were bonding pressure, time, and temperature, and the output parameter was a bonded ratio representing the strength of the void based on the extent to which the void was closed.

3. Results and Discussion

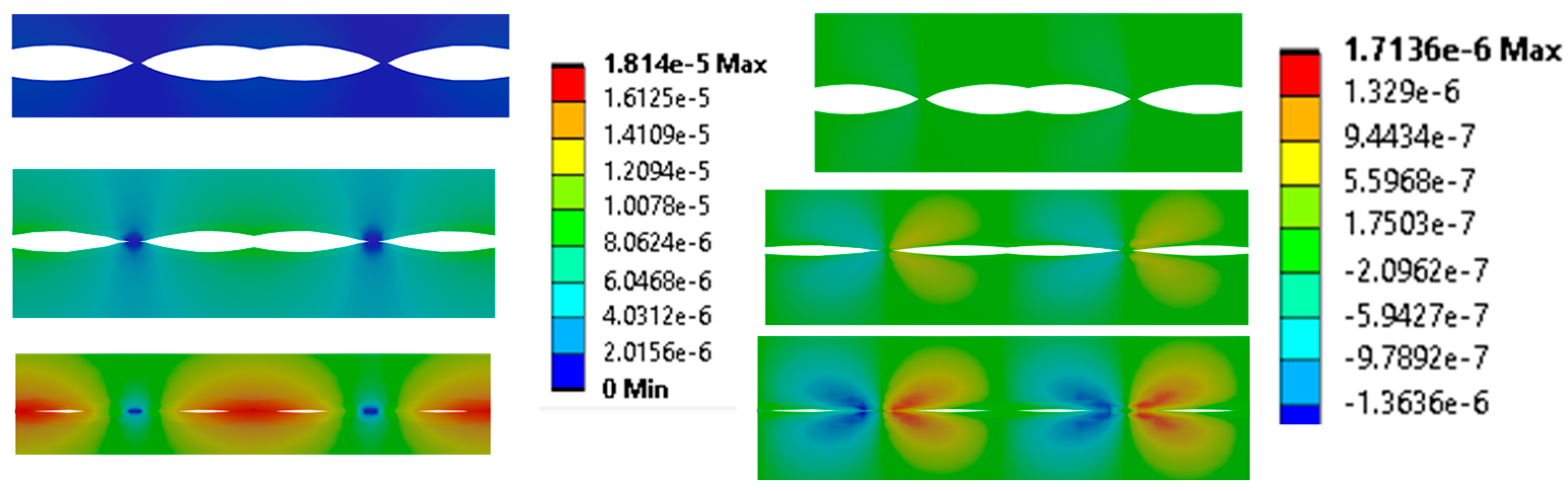
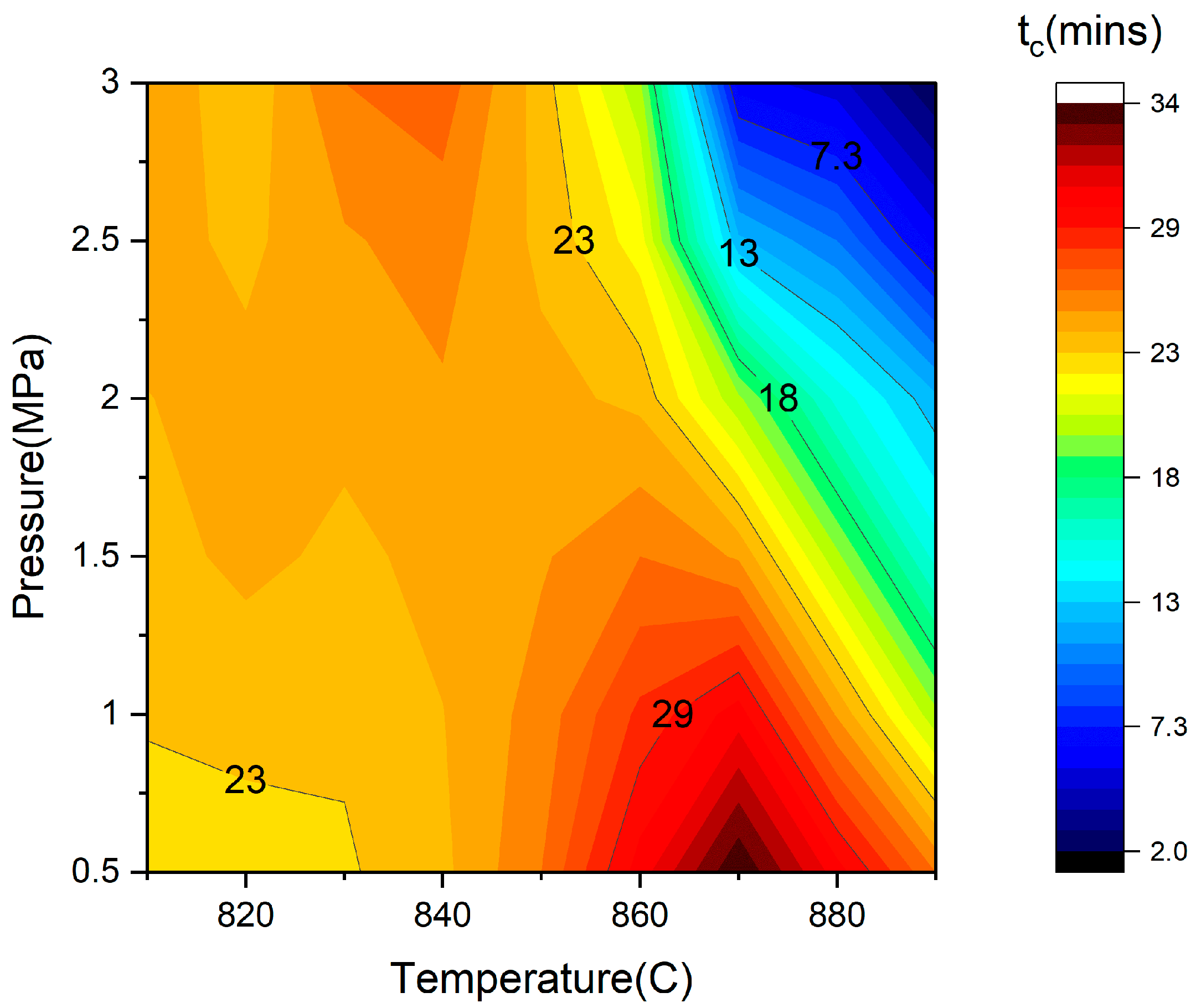
3.1. Contours

Simulation-generated contours vividly depict the progressive closure of voids over time, as shown in Figure 6. These visual representations highlight the roles temperature and pressure play in facilitating diffusion-driven processes. The contours provide a clear and intuitive understanding of the underlying mechanisms. Through the contours, this study establishes the temporal and spatial evolution of void closure, illustrating the key factors that drive the process. The model was used to predict the amount of diffusion that happened during the simulation by integrating with the numerical mathematical model.

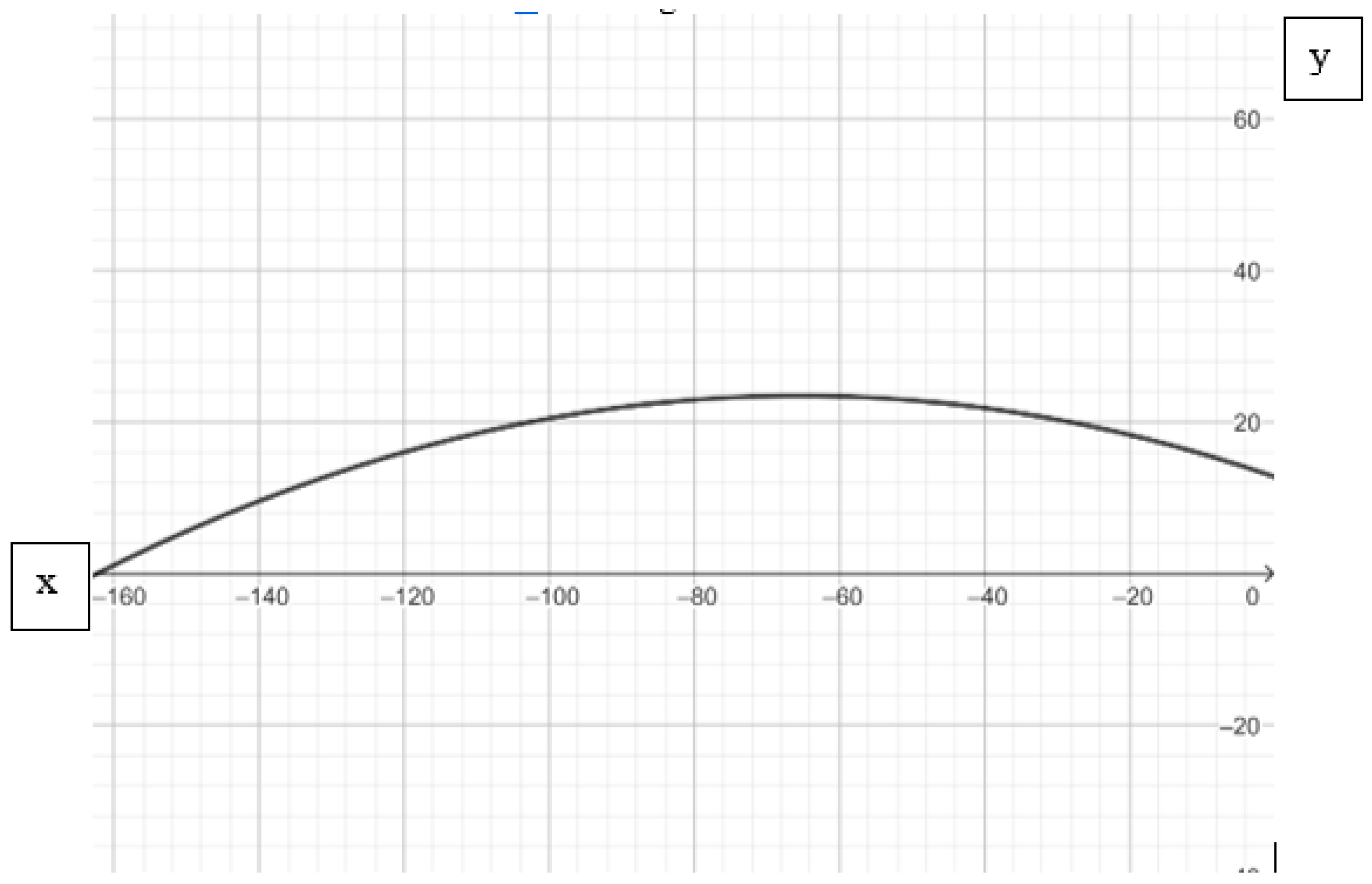
3.2. Numerical Derivatives

The numerical derivatives derived from the model quantify the relationship between key process parameters and void closure rates. These derivatives provide valuable insights into optimizing the process by identifying the most influential variables. These derivatives are also part of the numerical calculations used to find the bonded ratio. It can be seen from Figure 7 that the derivative is large at the start of the process but continues to decrease as the void starts to close, showing that the diffusion process slows down as the time passes.

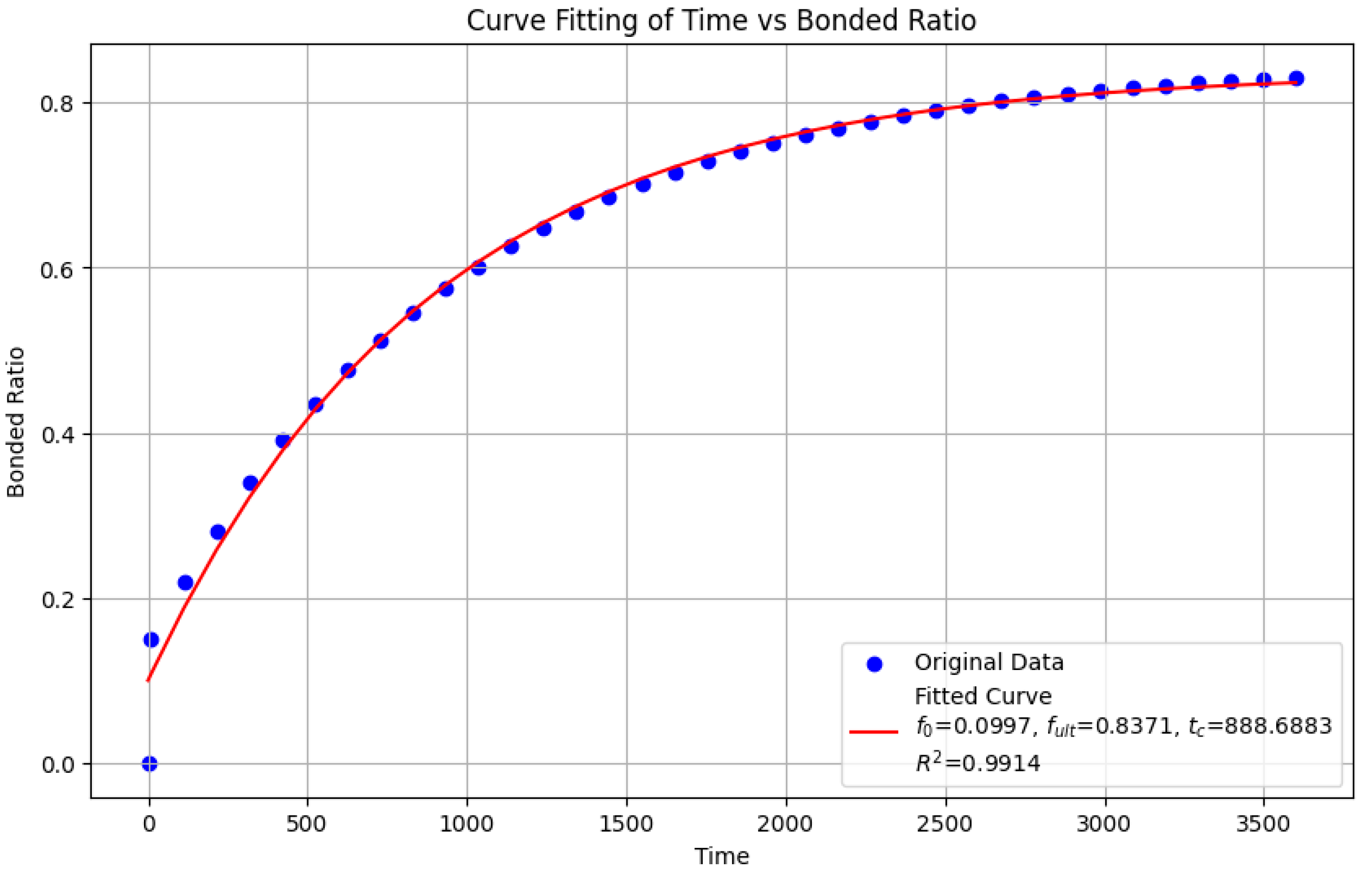
3.3. Curve-Fitting Results

The deformation values from the finite element simulation were integrated with the numerical calculation to calculate the value of the bonded ratio, and the result is shown in Figure 8. We can see that the slope of the bonded ratio with respect to time is greater at the start and the process slows down as the time passes because the difference in the curvature decreases as the time passes. Curve fitting was applied to the simulation data to visualize the behavior of the bonding process in a simulation. The curve-fitting results show such behavior because of the curvature of the void, which tends to slow down as the elliptical void changes to the circular one. The equation which was fitted in the model is given below:

$$f_t=9.97+\left(83.71-9.97\right)\left[1-exp\left(-{\displaystyle \frac{t}{888.68}}\right)\right]$$

Similarly, increased pressure enhances the bonding efficiency by reducing the time required for voids to close, as shown in Figure 9. It can be seen from the figure that the effect of temperature is much greater compared with the pressure on the critical time for the bonded ratio. This means that a small change in the temperature causes a greater change in critical temperature, keeping the pressure constant, as compared to the other scenario in which the temperature is kept constant and pressure is changed.

4. Conclusions

This study demonstrates how the simulated model is integrated with the numerical model to develop the diffusion void closure model. The void closure model accounts for the surface and bulk deformation based on the difference in curvature in the elliptical voids. The effects of temperature and pressure on the bonded ratio are discussed in this study. It is discussed in the study that the effect of temperature is more pronounced compared with the effect of pressure.