Analysis and Selection of Multiple Machine Learning Methodologies in PyCaret for Monthly Electricity Consumption Demand Forecasting ^†

Abstract

This study investigates the application of several machine learning models using PyCaret to forecast the monthly demand for electricity consumption; we analyze historical data of monthly consumption readings for the Cuajone Mining Unit of the company Minera Southern Peru Copper Corporation, recorded in the electricity yearbooks from the decentralized office of the Ministry of Energy and Mines in the Moquegua region between 2008 and 2018. We evaluated the performance of 27 machine learning models available in PyCaret for the forecast of monthly electricity consumption, selecting the three most effective models: Exponential Smoothing, AdaBoost with Conditional Deseasonalize and Detrending and ETS (Error-Trend-Seasonality). We evaluated the performance of these models using eight metrics: MASE, RMSSE, MAE, RMSE, MAPE, SMAPE, R2, and calculation time. Among the analyzed models, Exponential Smoothing demonstrated the best performance with a MASE of 0.8359, an MAE of 4012.24 and an RMSE of 5922.63; among the analyzed models, Exponential Smoothing demonstrated the best performance with a MASE of 0.8359, an MAE of 4012.24 and a RMSE of 5922.63, followed by AdaBoost with Conditional Deseasonalize and Detrending, while ETS also provided competitive results. Forecasts for 2018 were compared with actual data, confirming the high accuracy of these models. These findings provide a robust energy management and planning framework, highlighting the potential of machine learning methodologies to optimize electricity consumption forecasting.

1. Introduction

Predicting has always been fascinating; Thales of Miletus predicted an eclipse on 28 May 585 BC.

Since the invention of the electric light bulb in the 19th century, electric energy has been introduced into home lighting [1]. As a strategic and valuable resource, electric energy decisively determines the functioning of a chain of economic variables that influence a region’s economy and, therefore, a country. In the case of strategic companies in the country’s regions, it constitutes a convenient and valuable resource to make predictions about, as this would allow for more precise and efficient management [2].

The data from the research in this area are at the regional level. Due to this issue, it is possible to make projections regarding this valuable resource, which is becoming increasingly necessary to manage efficiently.

Electricity consumption forecasting has been the subject of extensive research, with numerous models and methodologies developed over the years. Traditional statistical methods, such as Exponential Smoothing and ARIMA, have been widely used for their simplicity and effectiveness in capturing linear patterns in time series data [3]. However, with the advent of machine learning, more sophisticated models have emerged, offering the potential to capture complex, non-linear relationships in the data.

Numerous machine learning models have been used to predict electricity consumption in recent years, each with advantages and disadvantages. For example, decision trees and random forests have received praise for their interpretability and robustness [4], while neural networks and support vector machines are known for their ability to handle large amounts of data and capture complex patterns [5].

PyCaret, an open source and low-code Python-based machine learning library, offers a variety of tools to automate machine learning workflows [6], such as Random Forest [7], Gradient Boosting [8], Light Gradient Boosting [9], Polynomial Trend Forecaster [10], Extreme Gradient Boosting [11], Theta Forecaster, ARIMA [12], Seasonal Naive Forecaster [13], Lasso Least Angular Regressor [14], Decision Tree with Conditional Deseasonalize and Detrending [15], Extra Trees Regressor [16], Gradient Boosting Regressor [17], Random Forest Regressor [18], Light Gradient Boosting Machine [19] Naive Forecaster [20], Croston [21], Auto ARIMA [22], and Bayesian Ridge [23]. By leveraging PyCaret, this study aims to systematically evaluate and compare 27 different machine learning models for forecasting monthly electricity consumption. We assess the models using eight evaluation metrics: MASE, RMSSE, MAE, RMSE, MAPE, SMAPE, R2, and computation time (TT) [6,24,25].

PyCaret offers a wide variety of machine-learning modules, such as regression, classification, anomaly detection, clustering, and natural language processing, allowing us to perform many machine learning tasks. PyCaret presents 27 machine learning models for the treatment of time series, and below is a detailed description of each method, including its creator, along with relevant bibliographic references, which can be seen in Table 1.

Table 1. Overview of Machine Learning Methods for Electricity Consumption Forecasting in PyCaret.

N°	Method	Originator(s)	Reference
1	Exponential Smoothing	Robert G. Brown (1956)	Forecasting: principles and practice [26].
2	Adaptive Boosting with Conditional Deseasonalization and Detrending	Yoav Freund and Robert Schapire (1997)	A decision–theoretic generalization of online learning and an application to boosting [27]
3	Error, Trend, Seasonal (ETS)	Hyndman et al. (2002)	Automatic time series forecasting: the forecast package for R [3].
4	Orthogonal Matching Pursuit with Conditional Deseasonalization and Detrending	Y. C. Pati, R. Rezaiifar, and P. S. Krishnaprasad (1993)	Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition [28].
5	K-Nearest Neighbors with Conditional Deseasonalization and Detrending	Evelyn Fix and Joseph Hodges (1951)	Discriminatory analysis: Nonparametric discrimination: Consistency properties [29].
6	Bayesian Ridge Regression with Conditional Deseasonalization and Detrending	Harold Jeffreys (1946); Arthur E. Hoerl and Robert W. Kennard (1970)	Ridge regression: Biased estimation for nonorthogonal problems [30].
7	Extra Trees Regressor with Conditional Deseasonalization and Detrending	Pierre Geurts, Damien Ernst, and Louis Wehenkel (2006)	Extremely randomized trees [31].
8	Random Forest Regressor with Conditional Deseasonalization and Detrending	Leo Breiman (2001)	Random forests [32].
9	Lasso Regression with Conditional Deseasonalization and Detrending	Robert Tibshirani (1996)	Regression shrinkage and selection via the lasso [33].
10	Elastic Net Regression with Conditional Deseasonalization and Detrending	Hui Zou and Trevor Hastie (2005)	Regularization and variable selection via the elastic net [34].
11	Ridge Regression with Conditional Deseasonalization and Detrending	Arthur E. Hoerl and Robert W. Kennard (1970)	Ridge regression: Biased estimation for nonorthogonal problems [30].
12	Linear Regression with Conditional Deseasonalization and Detrending	Carl Friedrich Gauss (1795)	Applied regression analysis [35].
13	Least Angle Regression with Conditional Deseasonalization and Detrending	Bradley Efron, Trevor Hastie, Iain Johnstone, and Robert Tibshirani (2004)	Least angle regression [36].
14	Theta Forecasting Model	Assimakopoulos and Nikolopoulos (2000)	The theta model: a decomposition approach to forecasting [37].
15	Gradient Boosting Regressor with Conditional Deseasonalization and Detrending	Jerome H. Friedman (2001)	Greedy function approximation: A gradient boosting machine [38].
16	Light Gradient Boosting Machine with Conditional Deseasonalization and Detrending	Guolin Ke, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, and Tie-Yan Liu (2017)	LightGBM: A highly efficient gradient boosting decision tree [39].
17	Huber Regressor with Conditional Deseasonalization and Detrending	Peter J. Huber (1964)	Robust estimation of a location parameter [40].
18	Seasonal and Trend decomposition using Loess Forecasting (STLF)	Cleveland et al. (1990)	STL: A seasonal-trend decomposition procedure based on loess [41].
19	Extreme Gradient Boosting with Conditional Deseasonalization and Detrending	Tianqi Chen and Carlos Guestrin (2016)	XGBoost: A scalable tree boosting system [42].
20	AutoRegressive Integrated Moving Average (ARIMA)	George Box and Gwilym Jenkins (1970)	Time series analysis: forecasting and control [43].
21	Seasonal Naive Forecaster	Commonly used technique in time series forecasting	Forecasting: principles and practice [26].
22	Polynomial Trend Forecaster	Based on polynomial regression techniques	Applied regression analysis [35].
23	Decision Tree Regressor with Conditional Deseasonalization and Detrending	Breiman et al. (1984)	Classification and regression trees [32].
24	Croston’s Forecasting Model	J. D. Croston (1972)	Forecasting and stock control for intermittent demands [44].
25	Automated ARIMA (Auto ARIMA)	Hyndman et al. (2008)	Automatic time series forecasting: the forecast package for R [3].
26	Naive Forecaster	Commonly used technique in time series forecasting	Forecasting: principles and practice [26].
27	Ensemble of Mainstream Media Forecasters	Concept based on combining multiple forecasting models	Forecast combinations [45].

The objectives of this research are:

• To evaluate the performance of 27 machine learning models available in PyCaret for forecasting monthly electricity consumption.
• To identify the three most effective models based on a comprehensive analysis of eight evaluation metrics.

2. Materials and Methods

2.1. Study Area

The study was carried out in the Mariscal Nieto province of the department of Moquegua, using information from the electrical yearbooks from 2008 to 2018 on the monthly electrical energy consumption of the Cuajone Mining Unit of the mining and metallurgical company Southern Peru Copper Corporación de Energía y Minas of the Moquegua Region.

The Southern Copper Corporation (México Group) remains active in adding larger volumes of copper to national production, supporting Peru’s path to becoming the world’s leading producer, due to the growing demand for copper in support of the energy transition towards renewable sources [46]. The location of the mining company Southern Peru Copper Corporation can be seen in Figure 1.

Figure 1. Location of Moquegua.

2.2. Methodology

We used the software Python 3.11.7 | packaged by Anaconda, Inc. based in Austin, TX, United States (main, 15 December 2023, 18:05:47) [MSC v.1916 64 bit (AMD64)] on win32 and PyCaret 3.3.2. This is a powerful tool for processing and forecasting time series through its libraries, available in the Repository (CRAN).

The study utilizes monthly electricity consumption data from the Southern Peru Copper Corporation from 2008 to 2017. We used the data for 2018 for validation and comparison with forecasted values. The methodology involves the following steps and workflow of methodology in PyCaret, as seen in Figure 2:

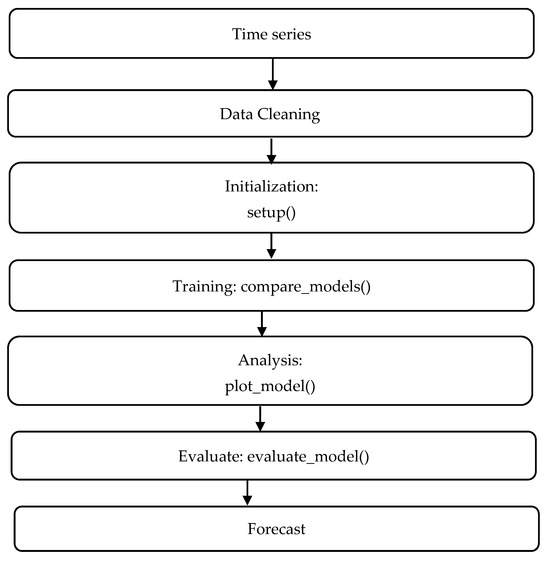
Figure 2. Workflow of methodology in Pycaret.

3.

Data Collection: We extracted historical monthly electricity consumption data from electrical yearbooks.

4.

Data Preprocessing: We handled missing values and normalized the data. We also applied seasonal decomposition to understand underlying patterns.

5.

Feature Engineering: We created lag features and rolling statistics to capture temporal dependencies.

6.

Model Selection: Various models were selected, including Exponential Smoothing, Adaptive Boosting with Conditional Deseasonalization and Detrending, and ETS.

7.

Model Training and Tuning: We trained the models using PyCaret and tuned the hyperparameters using GridSearchCV.

8.

Evaluation Metrics: Models were evaluated based on MASE, RMSSE, MAE, RMSE, MAPE, SMAPE, R2, and computation time.

PyCaret’s variety of features makes the model selection processes easier. These functions are initialization, model comparison, instruction, analysis model, and evaluation model. The Setup () function in PyCaret allows you to direct the preprocessing and ML workflow. This involves entering the dataset and the slope or target variable, which must be carried out before.

PyCaret trains multiple models based on performance metrics and ranks them from best to worst. The compare_models() function ranks models based on their metrics and also considers the time this process takes, which varies depending on the size and type of data file. The plot_model() function is included in PyCaret, allowing visualization of the capacity of trained machine learning models.

2.2.1. Data

The scope of the study includes the monthly consumption readings recorded in the electricity yearbooks of the decentralized office of the Ministry of Energy and Mines in the Moquegua region between 2008 and 2018, in megawatt-hours (MWh) [47].

2.2.2. Application of Metrics

The metrics that allow the analysis and selection of the best model are:

1. 

Mean Absolute Scaled Error (MASE):

MASE is a measure of forecast accuracy that scales the mean absolute error based on the in-sample absolute mean mistake from a naïve forecast method (usually the previous period value). It is particularly useful for comparing forecast accuracy across different data scales.

$$\mathrm{MASE}= {\displaystyle \frac{\frac{1}{n}{\sum }_{t=1}^n\left|y_t-{\widehat{y}}_t\right|}{\frac{1}{n-1}{\sum }_{t=2}^n\left|y_t-y_{t-1}\right|}}$$

where $y_t$ is the actual value, ${\widehat{y}}_t$ is the forecasted value, and $n$ is the number of observations.

2. 

Root Mean Squared Scaled Error (RMSSE):

RMSSE is similar to MASE but uses squared errors instead of absolute errors. It measures the average magnitude of the forecast errors, penalizing more significant errors more heavily.

$$\mathrm{RMSSE}= \sqrt{{\displaystyle \frac{\frac{1}{n}{\sum }_{t=1}^n{\left(y_t-{\widehat{y}}_t\right)}^2}{\frac{1}{n-1}{\sum }_{t=2}^n{\left(y_t-y_{t-1}\right)}^2}}}$$

3. 

Mean Absolute Error (MAE):

MAE measures the average magnitude of the errors in a set of forecasts without considering their direction. It is the average of absolute differences between forecasted and actual observations over the test sample.

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}{\sum }_{t=1}^n\left|y_t-{\widehat{y}}_t\right|$$

4. 

Root Mean Squared Error (RMSE):

RMSE measures the square root of the average of the squared differences between forecasted and actual values. Compared to MAE, it is more sensitive to large errors.

$$\mathrm{RMSE}= \sqrt{{\displaystyle \frac{1}{n}}{\sum }_{t=1}^n({y_t-{\widehat{y}}_t)}^2}$$

5. 

Mean Absolute Percentage Error (MAPE):

MAPE expresses forecast accuracy as a percentage. It is the average of the absolute percentage errors of forecasts. It is scale-independent but can be biased if actual values are minimal.

$$\mathrm{MAPE} ={\displaystyle \frac{1}{n}}{\sum }_{t=1}^n\left|{\displaystyle \frac{y_t-{\widehat{y}}_t}{y_t}}\right|\times 100\%$$

6. 

Symmetric Mean Absolute Percentage Error (SMAPE):

SMAPE is an alternative to MAPE that symmetrically treats over- and under-forecasts. It is more robust when dealing with low actual values.

$$SMAPE={\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\displaystyle \frac{\left|y_i-{\widehat{y}}_i\right|}{\frac{\left|y_i\right|+\left|{\widehat{y}}_i\right|}{2}}}\times 100\%$$

7. 

R2 Comparison:

R2 indicates the proportion of the variance in the dependent variable that is predictable from the independent variables. It ranges from 0 to 1, with higher values indicating better model performance.

$$R2=1-{\displaystyle \frac{\sum _{t=1}^n{\left(y_t-{\widehat{y}}_t\right)}^2}{\sum _{t=1}^n{\left(y_t-\widehat{y}\right)}^2}}$$

where y represents the mean of the actual values.

8. 

Computation Time (TT):

Computation Time (TT) is the time it takes the model to train and generate forecasts. It is a crucial metric in practical applications where time efficiency is essential.

Measurement: TT is typically measured in seconds (s), and we record it using system functions that track the duration of the forecasting process.

3. Results and Discussion

3.1. Data Cleaning and Initialization

Data cleaning and imputation were automatic and fast for the entire series. For the Setup (), the following is considered: the target is consumption, the total data items consist of 132 for training, 120 reserved, and 12 for testing; we reserve these last readings for the validation of the forecast corresponding to the year 2018, the cross-validation is with k-fold = 3 and the rest in the standard PyCaret configuration.

3.2. Model Comparison

PyCaret chooses the best_model with the compare_models() function, which uses all eight metrics. Figure 3a,b compares performance metrics between different models and provides a summary of the best-performing models based on the combined metrics.

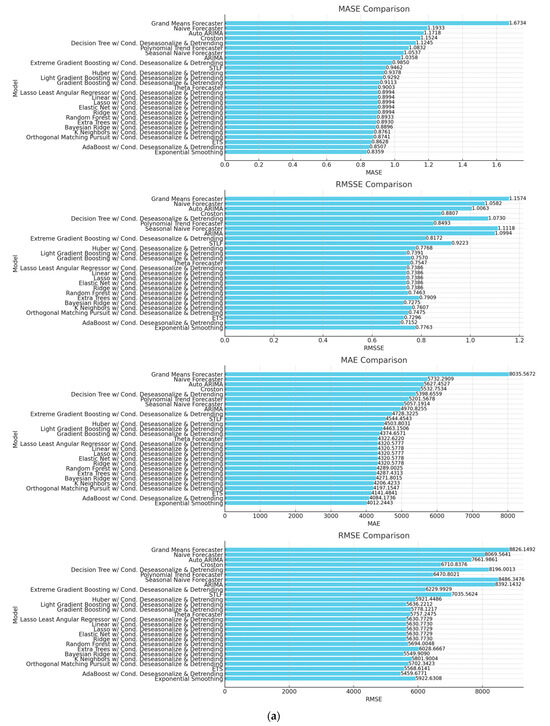
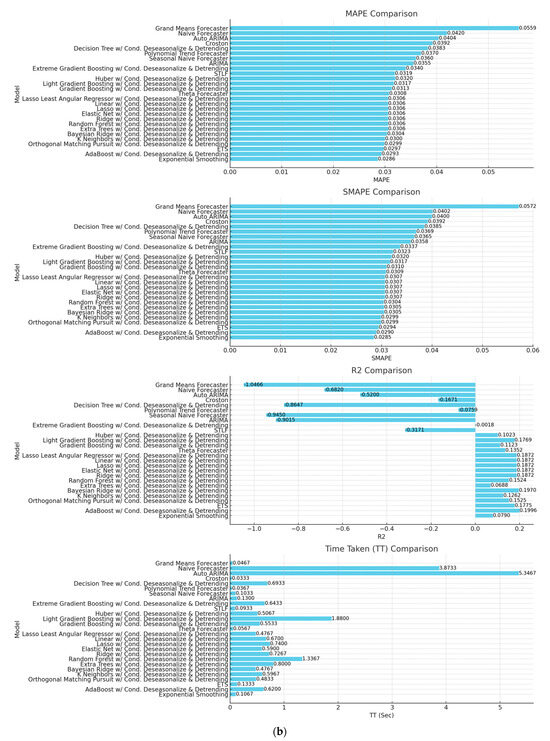
Figure 3. (a) Comparison of eight metrics. (b) Comparison of eight metrics.

The bar charts above compare the performance of different models based on various metrics. We summarize the critical observations:

MASE and RMSSE:

Top Models: Exponential Smoothing, AdaBoost with Conditional Deseasonalize and Detrending, ETS.

Observation: Exponential Smoothing shows the lowest MASE and RMSSE values, indicating it performs well regarding these error metrics.

MAE and RMSE:

Top Models: Exponential Smoothing, AdaBoost with Conditional Deseasonalize and Detrending, ETS.

Observation: Exponential Smoothing has the lowest MAE and RMSE, making it a strong candidate for minimizing absolute and squared errors.

MAPE and SMAPE:

Top Models: Exponential Smoothing, AdaBoost with Conditional Deseasonalize and Detrending, ETS.

Observation: These models consistently show lower values for MAPE and SMAPE, indicating better performance in percentage error metrics.

R2:

Top Models: AdaBoost with Conditional Deseasonalize and Detrending, ETS.

Observation: AdaBoost with Conditional Deseasonalize and detrending shows the highest R2 value, indicating that it explains the most variance in the data.

TT (Sec):

Top Models (Least Time): Exponential Smoothing, ETS.

Observation: Exponential Smoothing and ETS are among the fastest models, making them efficient in terms of computation time.

Recommendations

Best Overall Model: Exponential Smoothing

Reason: It consistently performs well across all error metrics and has a low computation time.

Runner-Up Models:

AdaBoost with Conditional Deseasonalize and Detrending: Shows high R2 and good performance across other metrics.

ETS: Good balance of performance and computation time.

We should consider these models for forecasting monthly electricity consumption demand due to their strong performance across multiple metrics and efficiency in computation.

3.3. Model Creation and Training

When creating the models, the hyperparameters are adjusted through cross-validation with k-fold = 3. The results of the 3 models are shown in Table 2 and Figure 4.

Table 2. Cross-validation for the three best-performing models.

Exponential Smooth		Cross-validation
	cutoff	MASE	RMSSE	MAE	RMSE	MAPE	SMAPE	R2
0	2014-12	0.7906	0.7349	3793.6623	5544.2617	0.0263	0.027	0.2432
1	2015-12	0.7782	0.8593	3756.6967	6536.8518	0.0283	0.0273	0.1185
2	2016-12	0.9387	0.7348	4486.3738	5686.779	0.0311	0.0314	−0.1246
Mean	NaT	0.8359	0.7763	4012.2443	5922.6308	0.0286	0.0285	0.079
SD	NaT	0.0729	0.0587	335.5997	438.1996	0.0019	0.002	0.1527
Ada Boost		Cross-validation
	cutoff	MASE	RMSSE	MAE	RMSE	MAPE	SMAPE	R2
0	2014-12	0.6591	0.5277	3162.6573	3981.5599	0.0222	0.0224	0.6097
1	2015-12	0.9064	0.9421	4375.4225	7167.3498	0.0327	0.0318	−0.0597
2	2016-12	0.9865	0.6758	4714.441	5230.1216	0.0329	0.0328	0.0488
Mean	NaT	0.8507	0.7152	4084.1736	5459.6771	0.0293	0.029	0.1996
SD	NaT	0.1394	0.1715	666.147	1310.6833	0.005	0.0047	0.2934
ETS		Cross-validation
	cutoff	MASE	RMSSE	MAE	RMSE	MAPE	SMAPE	R2
0	2014-12	0.7565	0.5799	3630.2501	4375.3848	0.0256	0.0259	0.5287
1	2015-12	0.827	0.9246	3992.0024	7033.912	0.0301	0.0289	−0.0206
2	2016-12	1.0048	0.6844	4802.1997	5296.5456	0.0334	0.0335	0.0245
Mean	NaT	0.8628	0.7296	4141.4841	5568.6141	0.0297	0.0294	0.1775
SD	NaT	0.1045	0.1443	489.983	1102.2576	0.0032	0.0031	0.249

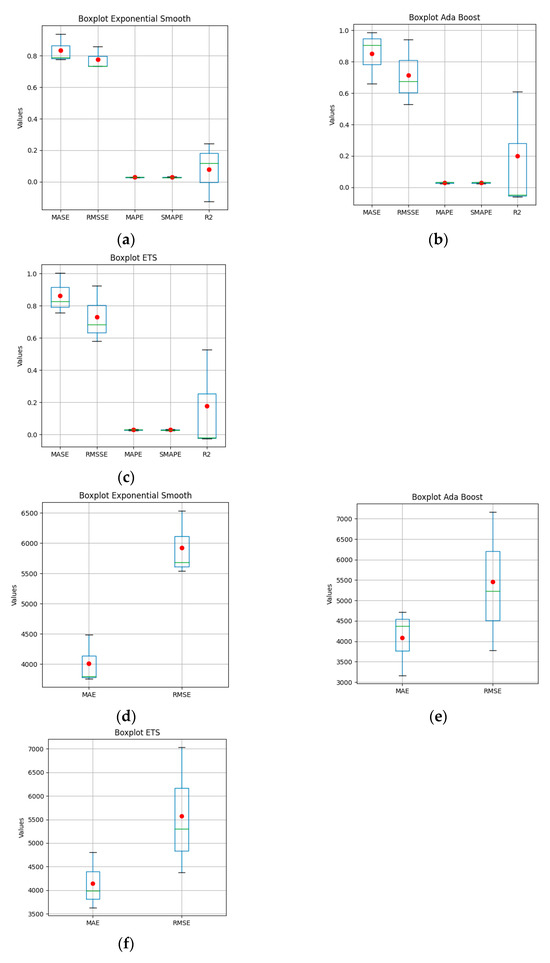
Figure 4. Cross-validation boxes and whiskers of the three best models with the metrics MASE, RMSE, MAPE, SMAPE and R2 between −0.1246 and 1.00481 (a–c) and the metrics MAE and RMSE between 3162.6573 and 7167.3498 (d–f).

Figure 4 shows the mean and variance and a minimum deviation in their means. Figure 4a–c corresponds to the values of the means and their deviations between −0.1246 and 1.0048. Figure 4d–f corresponds to the means values and their deviations between 3162.6573 and 7167.3498.

3.4. Model Comparison

We show the forecasts in Table 3 and Figure 5.

Table 3. Accurate readings and forecasting readings of electricity consumption demand for 2018.

		Forecasting Readings
Month	Real Readings	Exponential Smooth	Ada Boost	ETS
January	142,750	148,308.1503	151,519.7874	148,628.8883
February	133,250	135,222.6153	138,284.8118	136,198.3163
March	145,600	149,447.2654	149,085.8093	150,919.0335
April	143,100	142,234.6333	141,893.4414	142,582.7082
May	145,000	150,585.6266	149,222.6028	150,645.0903
June	150,250	146,790.2941	146,041.0431	147,550.7761
July	155,750	151,543.3057	152,364.0477	151,849.2819
August	158,200	14,6360.584	142,519.8809	142,832.7324
September	153,150	140,594.03	136,103.4339	137,931.3421
October	163,400	142,708.9193	143,023.5895	144,914.2118
November	143,600	143,898.9958	146,144.4833	146,119.9649
December	143,500	151,008.7511	149,992.7002	150,895.2123

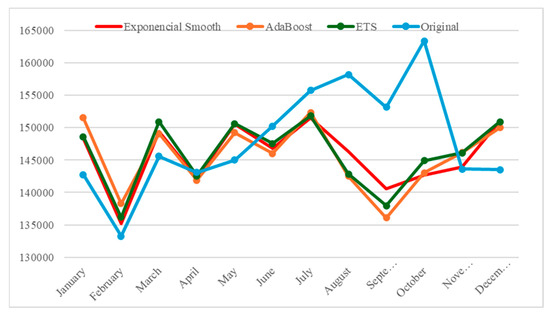
Figure 5. Accurate readings and forecasting readings of electricity consumption demand for 2018.

Analyzing Table 3 and Figure 5, we observe that the forecast data for electricity consumption demand is significant in most months except for August, September, and October, which represents more than 75% acceptance of the forecast referring to the consumption of the year 2018.

3.5. Forecast Validation

Below, Table 4 and Figure 6, Figure 7 and Figure 8 show the metrics for comparing the actual value and the forecast of monthly readings for the 2018 forecast.

Table 4. Metrics of the forecasting readings.

Model	MASE	RMSSE	MAE	RMSE	MAPE	SMAPE	R2
Exponential Smoothing	1.3373	1.0959	6532.4698	8629.4811	0.0427	0.0437	−0.1818
AdaBoostRegressor	1.5772	1.2503	7704.5632	9845.2811	0.0507	0.0521	−0.5383
ETS	1.4653	1.1574	7157.9544	9113.6632	0.047	0.0481	−0.3181

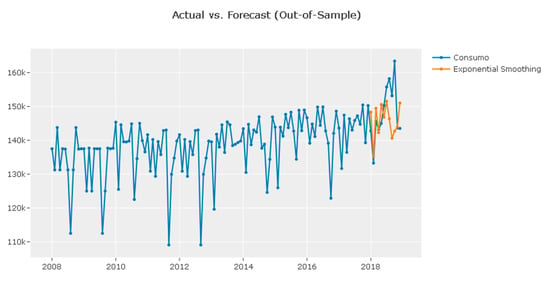
Figure 6. Dataset and its forecast, Exponential Smoothing.

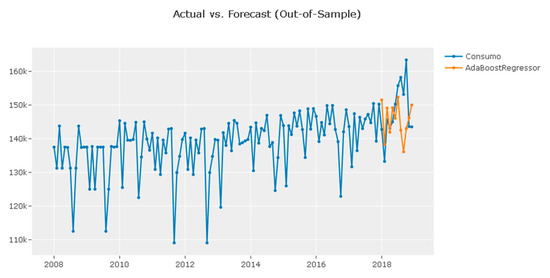
Figure 7. Dataset and its forecast, Ada boost Regressor.

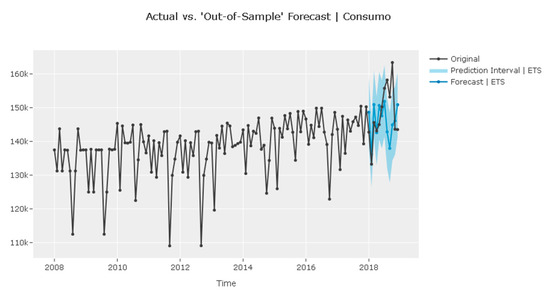
Figure 8. Dataset and its forecast, ETS.

Table 4 and Figure 6 show the electricity consumption prediction metrics for the year 2018. The Exponential Smoothing model has the lowest values for all evaluation metrics (MASE, RMSSE, MAE, RMSE, MAPE, SMAPE) and the least negative R2. Therefore, it is the best-performing model among those listed.

4. Conclusions

This study demonstrates that PyCaret’s machine learning models, particularly exponential smoothing and adaptive boosting with deseasonalization and conditional detrending, can effectively forecast monthly electricity consumption in industrial environments. These models provide accurate predictions and can be critical for energy planning and management. Future research should explore integrating additional external factors and advanced deep-learning models to improve forecast accuracy.