Abstract
Multi-criteria decision-making (MCDM) methods represent an efficient mathematical tool for making selections between several alternatives which are seemingly similar and also when a large number of influential criteria need to be taken into consideration. In other words, MCDM methods make difficult choices easier, so that was the reason why they found applications in various areas of life, industry, science, etc. In mineral processing, when conducting scientific research or in industrial practice, it is often necessary to make different kinds of decisions based on several often-conflicting parameters such as technological, economic and environmental parameters. Making the wrong choices can affect the industrial process, result in additional expenses and endanger the health of workers and the environment, thus the application of MCDM methods can be the solution and give additional help in decision-making processes. In the past few decades, a large number of MCDM methods were developed, and some of them have found application in mineral processing for different purposes, such as the selection of various equipment (flotation machines, crushers, etc.), the selection of flotation collectors and other reagents used in mineral processing, and the selection of technologies for processing different raw materials, grinding circuits, and so on. In this paper, a comprehensive overview of the used MCDM methods and their applications regarding mineral preparation and processing will be given.
1. Introduction
Mineral processing represents a series of closely related technological processes (comminution, classification, concentration, dewatering, thickening, filtering, tailings disposal) in which the efficiency of the entire process depends on the efficiency of each individual process, or, it can be said that the entire chain is only as strong as the weakest link in it. This means that when managing some industrial processes, one should take into account a very large number of influencing factors, which in some cases can be a problem, especially if some of the parameters are outside of the set values, and it is not possible to control them in the right way.
It is noticeable that the problem of making strategic or operational management decisions in the preparation of mineral raw materials is not only complex but also very specific from the aspect of uncertainty, indeterminacy and the almost always present paucity and reliability of data. Based on the analysis of literary sources, it can be concluded that the problem has not been considered until the end or investigated in accordance with its importance.
In order to deal with this issue, support can be found in application of multiple- criteria decision-making (MCDM) methods, which represent an efficient mathematical tool for making selections between several alternatives which are seemingly similar and also when a large number of influential criteria need to be taken into consideration.
2. The Short History of MCDM
According to many authors, MCDM can be defined as a process of evaluating or ranking alternatives based on a set of mutually conflicting criteria [1,2,3,4].
Since the end of the last century, MCDM has been used for solving many decision-making problems, and as a result, numerous MCDM methods have been proposed, such as Simple Additive Weighting (SAW) by MacCrimon in 1968 [5], ELimination and Choice Expressing REality (ELECTRE) by Roy in 1968 [6], the Analytic Hierarchy Process (AHP) by Saaty in 1977 [7], the Technique for Ordering Preference by Similarity to Ideal Solution (TOPSIS) by Hwang and Yoon in 1981 [8], the Preference Ranking Organisation Method for Enrichment Evaluations (PROMEHTEE) by Brans in 1982 [9], the COmplex Proportional ASsessment (COPRAS) by Zavadskas et al. in 1994 [10] and VIsekriterijumska optimizacija i KOmpromisno Resenje (in Serbian), means Multicriteria Optimization and Compromise Solution (VIKOR) by Opricovic in 1998 [11].
In addition to the above MCDM methods, a significant emergence of newly proposed MCDM methods can also be observed, such as the Additive Ratio Assessment (ARAS) proposed by Zavadskas and Turskis in 2010 [12], the Multi-Objective Optimization by Ratio Analysis plus Full Multiplicative Form (MULTIMOORA) proposed by Brauers and Zavadskas in 2010 [13], the Weighted Aggregates Sum Product Assessment (WASPAS) proposed by Zavadskas et al. in 2012 [14], Evaluation Based on Distance from Average Solution (EDAS) proposed by Keshavarz Ghorabaee et al. in 2015 [15], the COmbined COmpromise SOlution (CoCoSo) proposed by Yazdani et al. in 2018 [16], and so on.
Many decision-making problems are related to the occurrence of inaccuracies, unreliability, or predictions. Therefore, the significant development and use of MCDM methods occurred after Zadeh proposed fuzzy set theory in 1965 [17]. Based on a fuzzy set theory, Bellman and Zadeh in 1970 proposed decision-making in a fuzzy environment and thus enabled the use of MCDM for solving more complex decision-making problems [18]. Certainly, the use of MCDM methods for solving decision-making problems in a fuzzy environment also required their adaptation for the use of fuzzy sets.
Significantly greater possibilities provided by fuzzy sets concerning the application of crisp numbers also influenced the proposal of new extensions of the fuzzy set theory, such as interval-valued fuzzy sets by Turksen in 1986 [19], intuitionistic fuzzy sets by Atanassov in 1986 [20], the neutrosophic set theory by Smarandache in 1998 [21], and so on.
The above-mentioned MCDM methods, as well as a considerable number of other MCDM methods and their extensions, have been applied so far for solving numerous decision-making problems in numerous areas, such as mining and mineral processing.
The procedure for solving decision-making problems using MCDM methods consists of several stages. Depending on the problem being solved, as well as its complexity, different authors have identified different stages in the process of solving the decision-making problem, but the following stages can be identified as common and significant:
- Identification of alternatives and selection of criteria for their evaluation;
- Criteria weights determination;
- Normalization;
- Aggregation;
- Ranking and selection.
There are several normalization procedures, and the following can be singled out as frequently used: the max normalization method, the max–min normalization method, the square-root normalization method and the logarithmic normalization method. Some MCDM methods can be used with any normalization method, such as the SAW method, while some methods prefer a certain type of normalization, such as the TOPSIS and VIKOR methods.
Different MCDM methods use different, especially for their proposed purpose, aggregations procedures or combine several aggregation procedures. Based on the approach used in aggregation procedures, MCDM methods can be classified into one of the following categories [22]:
- Pairwise Comparison Based Methods;
- Outranking Methods;
- Distance Based Methods;
- Other Methods.
The affiliation of certain previously mentioned MCDM methods to the mentioned categories is shown in Figure 1.
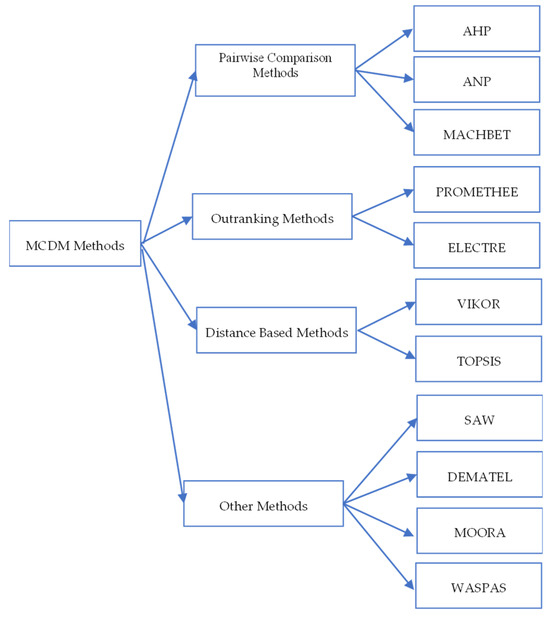
Figure 1.
Classification of MCDM methods.
Until now, MCDM methods have been used for solving many decision-making problems, which are documented in many professional and scientific journals. Figure 2 and Figure 3 shows the results of a search made in the WOS database using the keyword MCDM.
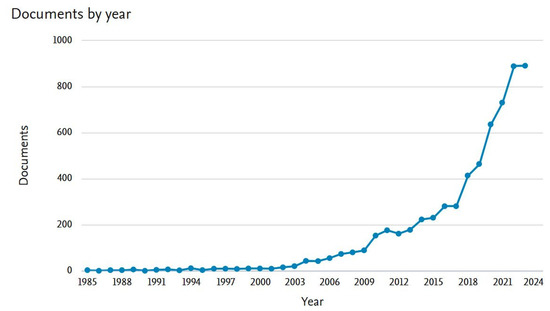
Figure 2.
Number of published articles by year.
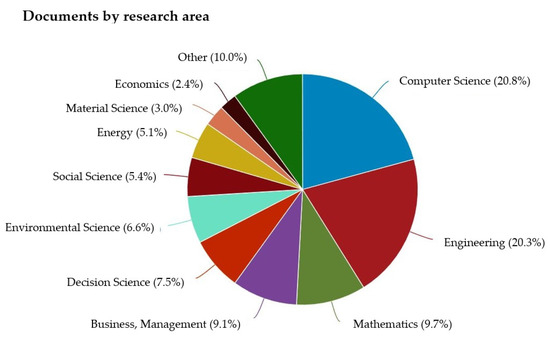
Figure 3.
Documents by research area.
3. Application of MCDM in Mineral Processing
In mineral processing, when conducting scientific research or in industrial practice, it is often necessary to make different kinds of decisions based on several often-conflicting parameters such as technological, economic and environmental parameters. Making the wrong choices can affect the industrial process, cause additional expenses and endanger the health of workers and the environment, thus the application of MCDM methods can be the solution and give additional help in decision-making processes.
The application of MCDM methods for solving different problems in mineral processing has become more and more common over the years as researchers from all over the world recognized their benefits.
Safari et al. [23] used AHP for the selection of a mineral processing plant location using eight criteria. Bakhtavar and Lotfian [24] have also carried out the selection of a mineral processing plant location by applying fuzzy AHP and grey MCDM. They used six criteria for ranking six different locations. Štirbanovic et al. [25] applied Rough Set Theory (RST) for choosing the location for a flotation tailings dump. The evaluation of ten potential locations was carried out using nine criteria.
Kostovic and Gligoric [26] used the TOPSIS method for the selection of a collector in the flotation of lead–zinc sulfide ore, while Štirbanovic et al. [27] applied the VIKOR method for the selection of a collector in porphyry copper ore flotation. Kursunogluhe et al. [28] investigated the selection of an acid type for the recovery of zinc from a flotation tailing using the AHP.
Baral et al. [29] applied TOPSIS along with a line graph and spider diagrams for the optimization of leaching parameters for the extraction of rare earth metals. TOPSIS was also used by Kursuncu et al. [30] for the optimization of leaching parameters of copper from malachite ore.
Wang et al. [31] have performed multi-objective optimization of an industrial grinding and classification process by applying MABAC (Multi-Attribute Border Approximation area Comparison), along with TOPSIS and VIKOR methods. Weights of attributes were determined using AHP, EW (entropy weight) and GRA (grey relational analysis) methods.
The selection of a grinding circuit was performed using the MOORA method [32] and interval-valued intuitionistic fuzzy sets [33]. For the selection of a lead-zinc flotation circuit design, the WASPAS method with a single-valued neutrosophic set was applied [34], while the selection of a copper-pyrite flotation circuit design was carried out by applying the Preference Selection Index (PSI) method [35].
The selection of the most appropriate primary crusher for iron ore between gyratory, double toggle jaw, single toggle jaw, high speed roll crusher, low speed sizer, impactor, hammer mill and feeder breaker crushers, applying the AHP method, was the aim of the study performed by Rahimdel and Ataei [36]. Sitorus and Brito-Parada [37] used the results from the previous study and applied the Integrated Constrained Fuzzy Stochastic Analytic Hierarchy Process (IC-FSAHP) to test its applicability for this kind of decision-making problem. The selection of a rougher flotation machine for the processing of copper sulphide ore using TOPSIS and VIKOR methods was performed by Štirbanović et al. [38]. The selection of a grinding machine, drilling machine and milling machine was carried out by Son et al. [39] using two different MCDM methods, the FUCA method (Faire Un Choix Adéquat) and the CURLI method (Collaborative Unbiased Rank List Integration).
Some other applications of MCDM in areas related to mineral processing are the selection of a process for aluminium separation from waste cables using TOPSIS and WASPAS methods [40] and the selection of the best technology for acid mine drainage (AMD) treatment by applying five different MCDM methods: TOPSIS, VIKOR, MOOSRA, WASPAS and CoCoSo [41].
4. Conclusions
Since the introduction of the first multi-criteria decision-making (MCDM) methods in 1968, SAW and ELECTRE, a large number of new methods were developed and they have found applications in many areas of life, science, industry, etc. Mineral processing, in both the scientific and industrial sense, is very convenient for the application of MCDM methods because the functioning of the different processes is influenced by many, often conflicting, parameters which must be taken into consideration when making various decisions. Many researchers have recognized this, especially in the past few years, and applied different MCDM methods for a number of purposes such as the selection of locations of mineral processing plants and flotation tailing dumps; the selection of various equipment (flotation machines, crushers, etc.); the selection of flotation collectors and other reagents used in mineral processing; and the selection of technologies for processing different raw materials, grinding circuits, and so on. However, there are still many possible applications of MCDM methods in mineral processing that can and should be investigated.
Author Contributions
Conceptualization, Z.Š. and D.S.; methodology, Z.Š.; software, D.S.; validation, Z.Š., D.S. and J.S.; formal analysis, I.I.; writing—original draft preparation, Z.Š., D.S., J.S. and I.I.; writing—review and editing, Z.Š. and D.S.; visualization, Z.Š., D.S. and J.S.; supervision, Z.Š.; funding acquisition, Z.Š. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia, grant number 451-03-47/2023-01/200131.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Levy, J.K. Multiple criteria decision making and decision support systems for flood risk management. Stoch. Environ. Res. Risk Assess. 2005, 19, 438–447. [Google Scholar] [CrossRef]
- Gebrezgabher, S.A.; Meuwissen, M.P.; Lansink, A.G.O. A multiple criteria decision making approach to manure management systems in the Netherlands. Eur. J. Oper. Res. 2014, 232, 643–653. [Google Scholar] [CrossRef]
- Qin, Y.; Qi, Q.; Shi, P.; Scott, P.J.; Jiang, X. Novel operational laws and power Muirhead mean operators of picture fuzzy values in the framework of Dempster-Shafer theory for multiple criteria decision making. Comput. Ind. Eng. 2020, 149, 106853. [Google Scholar] [CrossRef]
- Ardil, C.; Pashaev, A.M.; Sadiqov, R.A.; Abdullayev, P. Multiple Criteria Decision Making Analysis for Selecting and Evaluating Fighter Aircraft. Int. J. Transp. Veh. Eng. 2021, 13, 683–694. [Google Scholar]
- MacCrimon, K.R. Decision Making among Multiple Attribute Alternatives: A Survey and Consolidated Approach; Memorandum RM-4823-ARPA; Rand Memorandum: Santa Monica, CA, USA, 1968. [Google Scholar]
- Roy, B. Classement et choix en présence de points de vue multiples. Rev. Franiaise D’informatique Rech. Opérationnelle 1968, 2, 57–75. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making Methods and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Brans, J.P. Língénierie de la décision. Elaboration dínstruments dáide à la décision. Méthode PROMETHEE. In L’aide a la Décision: Nature, Instruments et Perspectives D’avenir; Nadeau, R., Landry, M., Eds.; Presses de l´Université Laval: Québec, QC, Canada, 1982; pp. 183–214. [Google Scholar]
- Zavadskas, E.K.; Kaklauskas, A.; Sarka, V. The new method of multicriteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Opricovic, S. Multicriteria Optimization of Civil Engineering Systems; Faculty of Civil Engineering: Belgrade, Serbia, 1998. (In Serbian) [Google Scholar]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multicriteria decision making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar] [CrossRef]
- Brauers, W.K.M.; Zavadskas, E.K. Project management by MULTIMOORA as an instrument for transition economies. Technol. Econ. Dev. Econ. 2010, 16, 5–24. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of weighted aggregated sum product assessment. Elektron. Ir Elektrotechnika 2012, 122, 3–6. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of Evaluation Based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Yazdani, M.; Zarate, P.; Zavadskas, E.K.; Turskis, Z. A Combined Compromise Solution (CoCoSo) method for multi-criteria decision-making problems. Manag. Decis. 2018, 57, 2501–2519. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision Making in a Fuzzy Environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Turksen, I.B. Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986, 20, 191–210. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy. Neutrosophic Probability, Set, and Logic; ProQuest Information and Learning: Ann Arbor, MI, USA, 1998. [Google Scholar]
- Kaya, I.; Colak, M.; Terzi, F. A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making. Energy Strategy Rev. 2019, 24, 207–228. [Google Scholar] [CrossRef]
- Safari, M.; Ataei, M.; Khalokakaie, R.; Karamozian, M. Mineral processing plant location using the analytic hierarchy process—A case study: The Sangan iron ore mine (phase 1). Min. Sci. Technol. 2010, 20, 0691–0695. [Google Scholar] [CrossRef]
- Bakhtavar, E.; Lotfian, R. Applying an integrated fuzzy gray MCDM approach: A case study on mineral processing plant site selection. Int. J. Min. Geo-Eng. 2017, 51, 177–183. [Google Scholar]
- Stirbanovic, Z.; Miljanovic, I.; Markovic, Z. Application of rough set theory for choosing optimal location for flotation tailings dump. Arch. Min. Sci. 2013, 58, 893–900. [Google Scholar]
- Kostovic, M.; Gligoric, Z. Multi-criteria decision making for collector selection in the flotation of lead–zinc sulfide ore. Miner. Eng. 2015, 74, 142–149. [Google Scholar] [CrossRef]
- Štirbanović, Z.; Stanojlović, R.; Sokolović, J.; Stanujkić, D.; Ćirić, N.; Miljanović, I.; Popović, G. Application of VIKOR method for selection of collector in porphyry copper ore flotation. In Proceedings of the XV International Mineral Processing and Recycling Conference, Belgrade, Serbia, 17–19 May 2023; Sokolović, J., Trumić, M., Eds.; Technical Faculty in Bor: Bor, Serbia, 2023; pp. 391–397. [Google Scholar]
- Kursunoglu, S.; Kursunoglu, N.; Hussaini, S.; Kaya, M. Selection of an appropriate acid type for the recovery of zinc from a flotation tailing by the analytic hierarchy process. J. Clean. Prod. 2021, 283, 124659. [Google Scholar] [CrossRef]
- Baral, S.S.; Shekar, K.R.; Sharma, M.; Rao, P.V. Optimization of leaching parameters for the extraction of rare earth metal using decision making method. Hydrometallurgy 2014, 143, 60–67. [Google Scholar] [CrossRef]
- Kurşuncu, B.; Yaraş, A.; Arslanoğlu, H. Application of multi criteria decision making methods to leaching process of copper from malachite ore. Sigma J. Eng. Nat. Sci. 2018, 36, 783–794. [Google Scholar]
- Wang, X.L.; Liu, L.M.; Duan, L.; Liao, Q. Multi-objective optimization for an industrial grinding and classification process based on PBM and RSM. IEEE/CAA J. Autom. Sin. 2023, 10, 2124–2135. [Google Scholar] [CrossRef]
- Stanujkic, D.; Magdalinovic, N.; Milanovic, D.; Magdalinovic, S.; Popovic, G. An efficient and simple multiple criteria model for a grinding circuit selection based on MOORA method. Informatica 2014, 25, 73–93. [Google Scholar] [CrossRef]
- Stanujkic, D.; Zavadskas, E.K.; Karabasevic, D.; Milanovic, D.; Maksimovic, M. An approach to solving complex decision-making problems based on IVIFNs: A case of comminution circuit design selection. Miner. Eng. 2019, 138, 70–78. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Baušys, R.; Stanujkic, D.; Magdalinovic-Kalinovic, M. Selection of lead-zinc flotation circuit design by applying WASPAS method with single-valued neutrosophic set. Acta Montan. Slovaca 2016, 21, 85–92. [Google Scholar]
- Magdalinović, N.; Štirbanović, Z.; Stanujkić, D.; Sokolović, J. Selection of copper-pyrite flotation circuit design by applying the Preference Selection Index Method. In Proceedings of the XIV International Mineral Processing and Recycling Conference, Belgrade, Serbia, 12–14 May 2021; Sokolović, J., Trumić, M., Eds.; Technical Faculty in Bor: Bor, Serbia, 2021; pp. 136–141. [Google Scholar]
- Rahimdel, M.J.; Ataei, M. Application of analytical hierarchy process to selection of primary crusher. Int. J. Min. Sci. Technol. 2014, 24, 519–523. [Google Scholar] [CrossRef]
- Sitorus, F.; Brito-Parada, P.R. Equipment selection in mineral processing—A sensitivity analysis approach for a fuzzy multiple criteria decision making model. Miner. Eng. 2020, 150, 106261. [Google Scholar] [CrossRef]
- Štirbanović, Z.; Stanujkić, D.; Miljanović, D.; Milanović, I. Application of MCDM methods for flotation machine selection. Miner. Eng. 2019, 137, 140–146. [Google Scholar] [CrossRef]
- Son, N.H.; Hieu, T.T.; Thang, N.M.; Tan, H.N.; Can, N.T.; Thao, P.T.; Bao, N.C. Choosing the best machine tool in mechanical manufacturing. EUREKA Phys. Eng. 2023, 2, 97–109. [Google Scholar] [CrossRef]
- Sokolović, J.; Stanujkić, D.; Štirbanović, Z. Selection of process for aluminium separation from waste cables by TOPSIS and WASPAS methods. Miner. Eng. 2021, 173, 107186. [Google Scholar] [CrossRef]
- Štirbanović, Z.; Gardić, V.; Stanujkić, D.; Marković, R.; Sokolović, J.; Stevanović, Z. Comparative MCDM Analysis for AMD Treatment Method Selection. Water Resour. Manag. 2021, 35, 3737–3753. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).