Abstract
In this paper, the authors present the results of modeling the movement of three methane molecules into a closed carbon nanotube. The main approach in this work is to model the interaction between methane molecules and the structure of a nanocapsule, which is a single-walled closed carbon nanotube. Descriptively, the interaction is represented using molecular dynamics approaches and the Lennard-Jones potential. Methane molecules in this model are material points corresponding to the centers of mass of the molecules. To solve the resulting equations of motion of molecules inside the nanotube, the classical Runge–Kutta method is used.
1. Introduction
The study of various properties of nanostructures and nanomaterials is of very wide interest for areas in which the processes of creating devices used in various fields of activity, such as science, medicine, ecology, and others, are studied. Carbon nanostructures based on such allotropic modifications of carbon as graphene, fullerenes, and nanotubes have useful properties that can be used to create nanoscale devices. In [1], the authors consider methods for placing various compounds in closed carbon structures, such as C60 fullerene, which is an important result for our work, and which is planned to be taken into account in our own studies. In [2], the results of the synthesis of clusters containing fullerene C82 are shown. Article [3] provides an overview of the applications of carbon nanotubes in such areas as the purification of drinking water from fluorine ions. Reference [4] is devoted to the study of metal-fullerene compounds. The authors of [5] are studying the possible use of nanosized containers to create clusters containing noble gases, with gas atoms creating Ne–Ne molecular-like structures.
It was shown in [6] that multiwalled nanotubes can be used as containers for drug use during functionalization using microwave radiation. With all the interest in the use of nanostructures in medicine, colleagues in [7] explore the potential risks of such use of carbon nanostructures. The paper [8] shows how molecular dynamics approaches can simulate the motion of large molecules, nanotori, and fullerenes. In the work of [9], quantum mechanical modeling of the behavior of a helium atom inside a fullerene sphere was considered. In one of the previous works of the team of authors [10], aspects of modeling the motion of a water molecule in the inner region of the C60 fullerene were studied.
2. Materials and Methods
For modeling, the structure of a closed single-walled carbon nanotube was chosen, which is 348 carbon atoms 12C, located in space so that, while remaining a surface crystal, this structure had a significant space inside, isolated by the surface of the tube from the external environment. Three model CH4 methane molecules were placed in this space, located on the symmetry axis of the nanotube as follows. One of the molecules was placed at a point along the x-axis corresponding to the middle of the nanotube length, and the other two molecules were placed on the left and right at the same distance equal to 1.2031 nm. The molecular coordinates along the y and z axes were set equal to zero. In fact, in this model, molecules are material points, and their spatial characteristics are not taken into account in any way other than using constants for methane in the Lennard-Jones potential. But from public considerations, the authors made the following calculation. Due to the fact that the model is built in the approaches of classical mechanics, we can assume that the methane molecule is a certain effective sphere, the radius of which can be roughly calculated as the sum of the bond length in the molecule between carbon atoms (0.1087 nm) and the radius of the hydrogen atom (0.053 nm), which gives a value of 0.1617 nm. This allows us to consider the molecules in this model as spheres with a diameter of 0.3234 nanometers, which, with the radius of the selected tube equal to 0.4736 nm and the diameter equal to 0.9472 nm, gives reason to believe that the molecules, in a certain sense, can freely move in the region of the tube, which is limited by its length, equal to 2.4062 nanometers, and the diameter indicated above. In the constructed model, it is allowed to approach material points to a distance up to the value of two molecular radii; to estimate these distances, it was calculated together with measurements of other system parameters.
The mathematical model was built from the following ideas existing in classical mechanics and molecular dynamics. The basic equation of dynamics for a moving body is taken as the basic equation. The right side of the equation is defined as the gradient from the potential for interaction with the nanostructure and other objects, taken with a minus sign:
where m is the mass of the methane molecule, ν is the velocity, t is the time, and V is the interaction potential. The Lennard-Jones potential is used as the interaction potential:
where ε is the energy constant, σ is the scale constant (V(σ) = 0), and r is the intermolecular distance. Using this, the acceleration for each of the moving particles is calculated. It is assumed that the carbon nanocell is fixed and there is no energy exchange with moving particles. The resulting equations of motion are reduced to the form in which it is necessary to calculate the derivatives of three coordinates for each of the three moving molecules and the derivatives of their spatial velocity components. That is, by adding initial conditions for coordinates and velocity components for each of the three molecules, the model is formalized as a Cauchy problem.
This statement of the problem indicates the need to use numerical methods for solving systems of ordinary differential equations. The authors of the work use the classical Runge–Kutta method of the fourth order of accuracy. The implementation of the method is carried out using the mathematical package MATLAB.
3. Results
It is important to note that this work is a theoretical study using a computer simulation of the movement of individual molecules inside an idealized nanocapsule, which is composed of a single-walled carbon nanotube and fullerene hemispheres. All atoms of the structure are fixed in space, and the calculation is performed with a “frozen” spatial configuration of the nanocell.
In the course of modeling the motion of molecules, the following initial configurations of the system were used. The positions of the carbon atoms that make up the nanotube were strictly specified and did not change during the simulation. The initial coordinates for the three methane molecules were given as already described in the previous section. The initial velocity components for three molecules were given and amounted to 10 m/s along each of the axes, which, in total, gave values of the velocity vectors of 10√3 m/s. The number of time steps was n = 105, with the step size dt = 2 × 10−7 ns. Figure 1 shows the movement of three methane molecules in a simulated nanocell. Figure 2a,b shows the trajectories in the x0y and x0z planes.
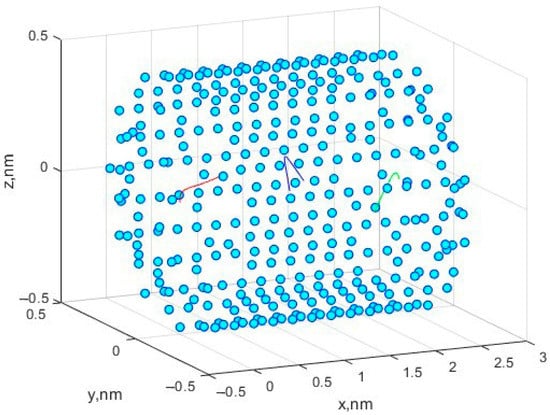
Figure 1.
Spatial configuration of a carbon nanocell and the trajectories of three methane molecules. The trajectory of the first molecule is marked in red, the trajectory of the second molecule is in blue, and the trajectory of the third is marked in green.
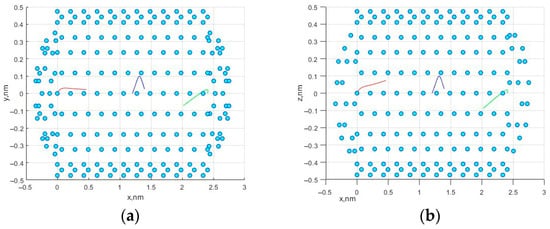
Figure 2.
Molecule trajectories in the different planes: (a) x0y plane; (b) x0z plane.
In addition, the velocity changes for three moving molecules are calculated. The results are presented in Figure 3.
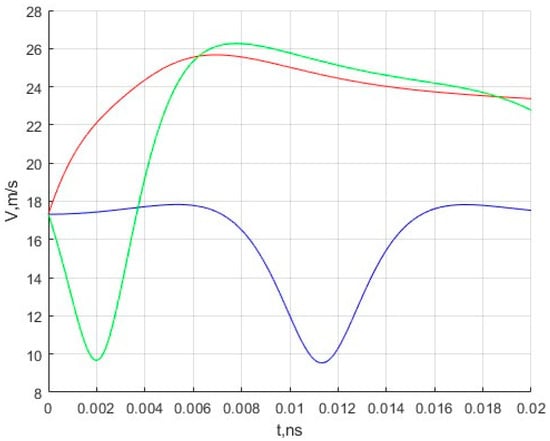
Figure 3.
Dependence of the speed of methane molecules on time. The red color indicates the speed of the first molecule, the blue color indicates the speed of the second, and the green color indicates the speed of the third.
Based on the nature of movement and change in velocities, we can say that, in general, this model successfully describes the movement of molecules in similar cells under the given restrictions and conditions imposed on the model during construction.
When analyzing the literature to verify and compare the results obtained, no data were found that could be directly compared with those presented in this paper. However, there are a number of results that are qualitatively and physically similar to those obtained in our simulations. In work [11], using the approaches of molecular dynamics and the Lennard-Jones potential, it is possible to study the processes of methane transport in pores, including through single-walled carbon nanotubes. In addition, the authors [11] show the distribution of molecules inside the nanotube during the flow of methane through it. Furthermore, it was shown in [12] that CO2 can be transported through a single-walled carbon nanotube embedded in a membrane. These results were also obtained by molecular dynamics methods. Reference [13] considers models of methane transport through graphene which model the complex pore boundary of shale.
4. Discussion
The results obtained during the simulation are of interest in that one can observe the characteristic movement of molecules in the inner region of the fullerene under the action of the potential field of the nanocell. The initial speed, as can be seen from Figure 3, does not change significantly and ranges from 9 to 27 m/s. Of course, these velocity values are very far from the most likely velocity of methane molecules under normal conditions. The authors plan to simulate motion at such speeds in the future.
Since this model does not implement energy exchange between the nanostructure and molecules, the total energy must be conserved with some computational accuracy. The authors made similar estimates in the following way. The total energy of the system was the sum of the kinetic and potential energies for all parts of the system. Because the motion of small objects is considered, the contribution of kinetic energy to its final value was many orders of magnitude lower than the effective values of potential energy. From the analysis of potential energy, it was revealed that its initial and final values do not differ within the limits allowed by the chosen numerical method, taking into account the representation of numbers in computer technology.
5. Conclusions
The results presented in this work can be used to improve the fundamental concepts of the interaction of carbon nanostructures with various chemical compounds, as well as to evaluate the potential possibility of using single-walled closed carbon nanotubes as nanocontainers for transporting or storing methane. In the course of modeling, it was noted that in order to develop a physical model of the process of motion of methane molecules inside a nanotube, it is necessary to take into account the spatial geometry of the molecules as well as the electrostatic effects arising from the spatial distribution of charges inside the molecules. This conclusion is supposed to be applied in estimating the movement of other molecules, such as H2O, CO2, and others.
Author Contributions
Conceptualization and methodology, E.T. and M.K.; software, writing—original draft preparation and visualization, M.K.; validation, formal analysis, supervision and project administration, E.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Murata, M.; Murata, Y.; Komatsu, K. Surgery of fullerenes. Chem. Commun. 2008, 46, 6083–6094. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Abella, L.; Yao, Y.R.; Sergentu, D.-C.; Yang, W.; Liu, X.; Zhuang, J.; Echegoyen, L.; Autschbach, J.; Chen, N. A charged diatomic triple-bonded U≡N species trapped in C82 fullerene cages. Nat. Commun. 2022, 13, 7192. [Google Scholar] [CrossRef] [PubMed]
- Chufa, B.; Murthy, H.; Gonfa, B.; Anshebo, T.Y. Carbon nanotubes: A review on green synthesis, growth mechanism and application as a membrane filter for fluoride remediation. Green Chem. Lett. Rev. 2021, 14, 647–664. [Google Scholar] [CrossRef]
- Niman, J.W.; Kamerin, B.S.; Villers, T.H.; Linker, T.M.; Nakano, A.; Kresin, V.V. Probing the presence and absence of metal-fullerene electron transfer reactions in helium nanodroplets by deflection measurements. Phys. Chem. Chem. Phys. 2022, 24, 10378–10383. [Google Scholar] [CrossRef] [PubMed]
- Saha, R.; Jana, G.; Pan, S.; Merino, G.; Chattaraj, P.K. How Far Can One Push the Noble Gases towards Bonding?: A Personal. Account. Mol. 2019, 24, 2933. [Google Scholar] [CrossRef] [PubMed]
- Thakur, C.K.; Karthikeyan, C.; Abou-Dahech, M.S.; Altabakha, M.M.A.M.; Al Shahwan, M.J.S.; Ashby, C.R., Jr.; Tiwari, A.K.; Babu, R.J.; Moorthy, N.S.H.N. Microwave-Assisted Functionalization of Multi-Walled Carbon Nanotubes for Biosensor and Drug Delivery Applications. Pharmaceutics 2023, 15, 335. [Google Scholar] [CrossRef] [PubMed]
- Pandey, R.P.; Vidic, J.; Mukherjee, R.; Chang, C.-M. Experimental Methods for the Biological Evaluation of Nanoparticle-Based Drug Delivery Risks. Pharmaceutics 2023, 15, 612. [Google Scholar] [CrossRef] [PubMed]
- Borodin, V.; Bubenchikov, M.; Bubenchikov, A.; Mamontov, D.; Azheev, S.; Azheev, A. Study of the Unstable Rotational Dynamics of a Tor-Fullerene Molecular System. Crystals 2023, 13, 181. [Google Scholar] [CrossRef]
- Poteryaeva, V.A.; Bubenchikov, M.A.; Bubenchikov, A.M.; Potekaev, A.I.; Kaparulin, D.S. The state of helium inside the fullerene. Izv. Vuzov. Fizika. 2022, 1, 156–164. [Google Scholar] [CrossRef] [PubMed]
- Khilchuk, M.; Tarasov, E. Numerical modeling of interaction of water molecule and fullerene C60. J. Phys. Conf. Ser. 2022, 2211, 012015. [Google Scholar] [CrossRef]
- Zhang, J.; Pei, G.; Zhang, L. Molecular Dynamics Simulation of Methane Gas Flow in Nanopores. Petroleum 2019, 5, 252–259. [Google Scholar] [CrossRef]
- Gao, Y.; Mao, D.; Wu, J.; Wang, X.; Wang, Z.; Zhou, G.; Chen, L.; Chen, J.; Zeng, S. Carbon Nanotubes Translocation through a Lipid Membrane and Transporting Small Hydrophobic and Hydrophilic Molecules. Appl. Sci. 2019, 9, 4271. [Google Scholar] [CrossRef]
- Zhao, Y.; Luo, M.; Liu, L.; Wu, J.; Chen, M.; Zhang, L.-H. Molecular dynamics simulation of shale gas transport in rough nanopores. J. Pet. Sci. Eng. 2022, 217, 110884. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).