Particle Swarm Optimization Algorithm for Gold Nanohole Array Design †
Abstract
:1. Introduction
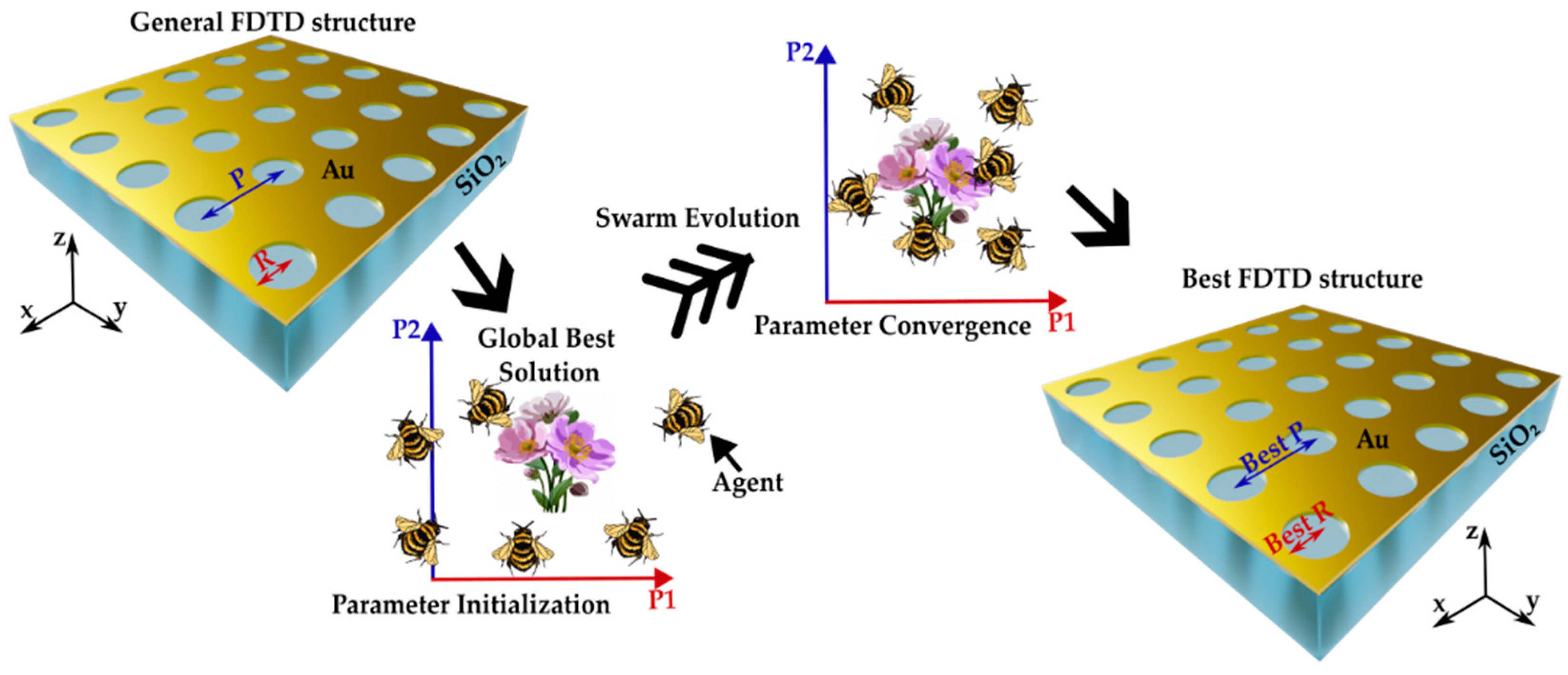
2. Materials and Methods
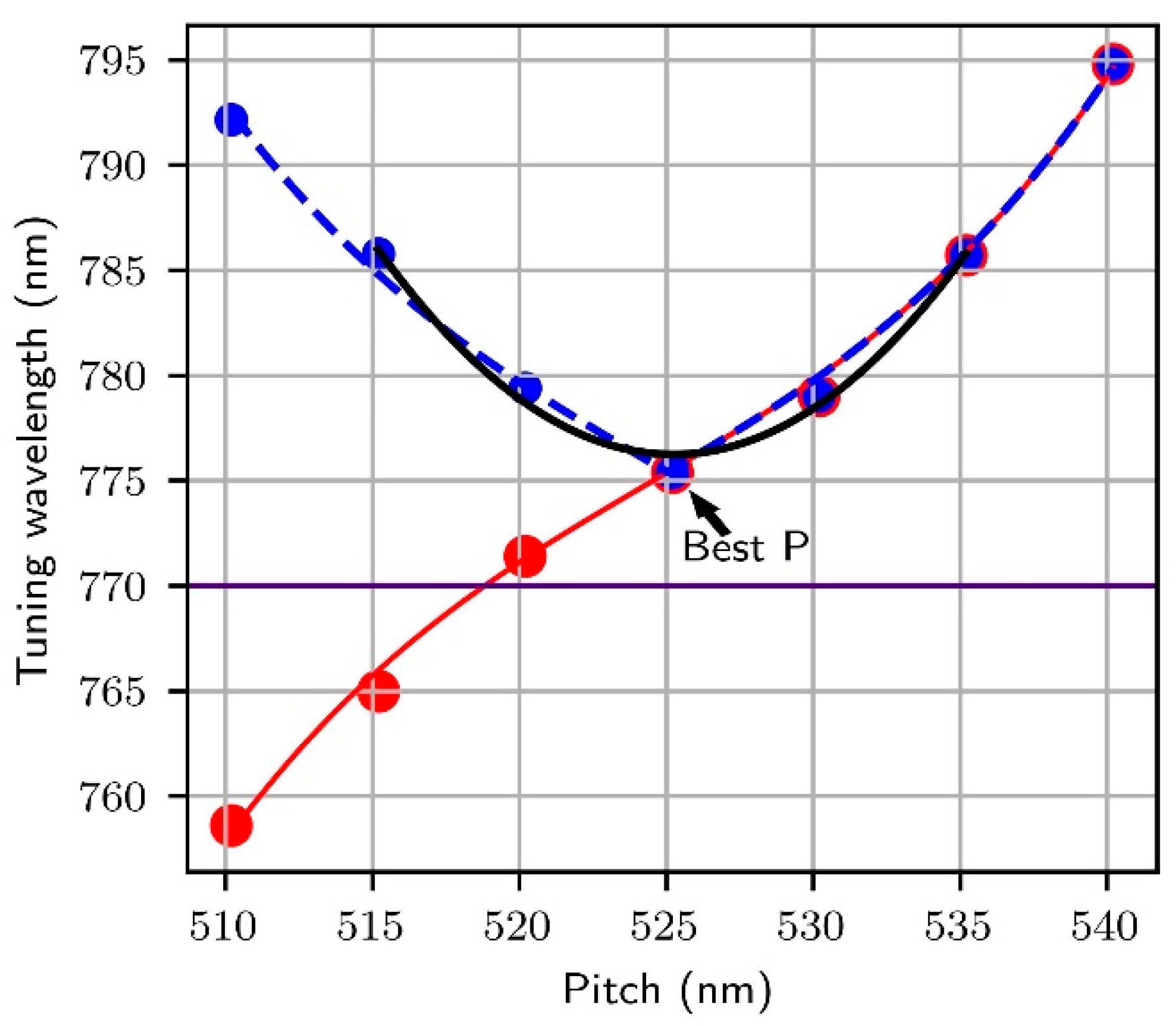
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin-Moreno, L.; Garcia-Vidal, F.J.; Lezec, H.J.; Pellerin, K.M.; Thio, T.; Pendry, J.B.; Ebbesen, T.W. Theory of extraordinary optical transmission through subwavelength hole arrays. Phys. Rev. Lett. 2001, 86, 1114. [Google Scholar] [CrossRef] [PubMed]
- Brolo, A.G.; Gordon, R.; Leathem, B.; Karen; Kavanagh, L. Surface Plasmon Sensor Based on the Enhanced Light Transmission through Arrays of Nanoholes in Gold Films. Langmuir 2004, 20, 4813–4815. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.L.; Leo, Y.S.; Zhou, X.; Ng, W.; Wong, T.I.; Deng, J. Localized surface plasmon resonance based point-of-care system for sepsis diagnosis. Mater. Sci. Energy Technol. 2020, 3, 274–281. [Google Scholar] [CrossRef]
- Escobedo, C. On-chip nanohole array based sensing: A review. Lab A Chip 2013, 13, 2445–2463. [Google Scholar] [CrossRef]
- Bottazzi, B.; Fornasari, L.; Frangolho, A.; Giudicatti, S.; Mantovani, A.; Marabelli, F.; Valsesia, A. Multiplexed label-free optical biosensor for medical diagnostics. J. Biomed. Opt. 2014, 19, 017006. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.; Rahmat-Samii, Y. Particle swarm optimization in electromagnetics. IEEE Trans. Antennas Propag. 2004, 52, 397–407. [Google Scholar] [CrossRef]
- Rahmat-Samii, Y. Genetic algorithm (GA) and particle swarm optimization (PSO) in engineering electromagnetics. In Proceedings of the 17th International Conference on Applied Electromagnetics and Communications, Dubrovnik, Croatia, 1–3 October 2003; pp. 1–5. [Google Scholar] [CrossRef]
- Zagaglia, L.; Floris, F.; O’Brien, P.A. Experimental Characterization of Particle Swarm Optimized Focusing Non-Uniform Grating Coupler for Multiple SOI Thicknesses. JLT 2021, 39, 5028–5034. [Google Scholar] [CrossRef]
- Zagaglia, L.; Floris, F.; O’Brien, P. Optimized Design Procedure for Low-cost Grating-couplers in Photonics-packaging. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium—Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019; pp. 234–241. [Google Scholar] [CrossRef]
- Lumerical Inc. Available online: https://www.lumerical.com/products/fdtd/ (accessed on 20 February 2022).
- h-ALO Photonic System for Adaptable MuLtiple-Analyte Monitoring of food-Quality. Available online: https://cordis.europa.eu/project/id/101016706/it (accessed on 30 May 2023).
- Zagaglia, L.; Demontis, V.; Rossella, F.; Floris, F. Particle swarm optimization of GaAs-AlGaAS nanowire photonic crystals as two-dimensional diffraction gratings for light trapping. Nano Express 2022, 3, 021001. [Google Scholar] [CrossRef]
- Passoni, M.; Floris, F.; Hwang, H.Y.; Zagaglia, L.; Carroll, L.; Andreani, L.C.; O’Brien, P. Co-optimizing grating couplers for hybrid integration of InP and SOI photonic platforms. AIP Adv. 2018, 8, 095109. [Google Scholar] [CrossRef]
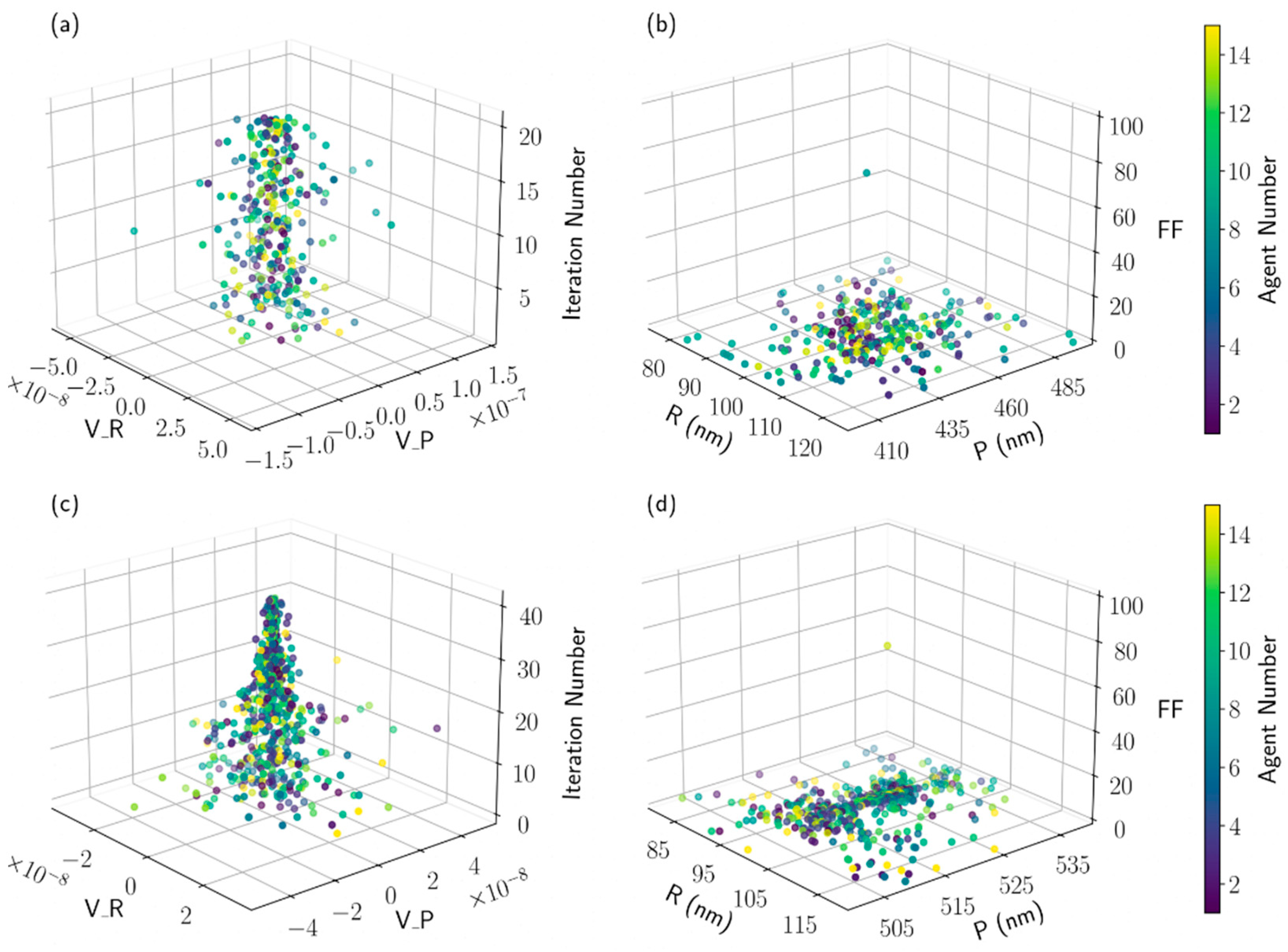

| Array | Agents | Iterations | R Range (nm) | P Range (nm) | Best R (nm) | Best P (nm) | λbest (nm) |
|---|---|---|---|---|---|---|---|
| Square | 15 | 20 | 75–125 | 400–500 | 97 | 454 | 763 |
| Hexagonal | 15 | 40 | 80–120 | 500–540 | 97 | 525 | 776 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Floris, F.; Angelini, M.; Marabelli, F. Particle Swarm Optimization Algorithm for Gold Nanohole Array Design. Mater. Proc. 2023, 14, 13. https://doi.org/10.3390/IOCN2023-14534
Floris F, Angelini M, Marabelli F. Particle Swarm Optimization Algorithm for Gold Nanohole Array Design. Materials Proceedings. 2023; 14(1):13. https://doi.org/10.3390/IOCN2023-14534
Chicago/Turabian StyleFloris, Francesco, Margherita Angelini, and Franco Marabelli. 2023. "Particle Swarm Optimization Algorithm for Gold Nanohole Array Design" Materials Proceedings 14, no. 1: 13. https://doi.org/10.3390/IOCN2023-14534
APA StyleFloris, F., Angelini, M., & Marabelli, F. (2023). Particle Swarm Optimization Algorithm for Gold Nanohole Array Design. Materials Proceedings, 14(1), 13. https://doi.org/10.3390/IOCN2023-14534







