Improved Low Complexity Predictor for Block-Based Lossless Image Compression ^†

Abstract

Lossless image compression has been studied and widely applied, particularly in medicine, space exploration, aerial photography, and satellite communication. In this study, we proposed a low-complexity lossless compression for image (LOCO-I) predictor based on the joint photographic expert group–lossless standard (JPEG-LS). We analyzed the nature of the LOCO-I predictor and offered possible solutions. The improved LOCO-I outperformed LOCO-I by a reduction of 2.26% in entropy for the full image size and reductions of 2.70, 2.81, and 2.89% for 32 × 32, 16 × 16, and 8 × 8 block-based compression, respectively. In addition, we suggested vertical/horizontal flip for block-based compression, which requires extra bits to record and decreases the entropy. Compared with other state-of-the-art (SOTA) lossless image compression predictors, the proposed method has low computation complexity as it is multiplication- and division-free. The model is also better suited for hardware implementation. As the predictor exploits no inter-block relation, it enables parallel processing and random access if encoded by fix-length coding (FLC).

1. Introduction

With the maturity of large-size display technology for cost reductions and the expansion of network communication bandwidth, high-resolution images such as 4 K and 8 K have become increasingly popular. Before compression, the size of high-quality images reaches several hundred megabytes. Therefore, lossless compression has become important.

Lossless image compression is conducted in the prediction and entropy encoding parts. The prediction part, however, is not limited to lossless usage. Prediction is applied to intra-frames in video coding such as high-efficiency video coding (HVEC) [1]. The main purpose of prediction is to reduce the spatial redundancy of input images. Residues, the differences between the real pixel value and predicted value, have a small interval that originates from 0 if the predictor is precise enough. According to information theory [2], the more the residue is centralized, the lower the entropy.

Lossless JPEG (JPEG-LS) with the median edge detector (MED) as its predictor [3] was renamed the LOCO-I algorithm, while context-based entropy coding was added after the prediction [4]. The predictor is simple and requires three of the causal neighbors of N, W, and NW (each representing North, West, and Northwest, respectively) and X as the predicted value (1). It uses the following equation:

$$X\triangleq \left\{\begin{array}{l}\min (W,N) if NW\ge \max (W, N) \\ \max (W,N) if NW\le \min (W, N)\\ W+N-NW otherwise\end{array}\right.$$

(1)

The MED is based on the fact that X is always chosen as the median value of A, B, and A + B $-$ C. Despite its simplicity, the MED has a higher accuracy than the gradient-adjusted predictor (GAP), which is used in context-based adaptive lossless image coding (CALIC) [5]. GAP predicts values according to whether the vertical/horizontal gradients nearby exceed specific thresholds. Therefore, GAP cannot fit various inputs. Another renowned predictor is the edge-directed predictor (EDP), which predicts pixel values based on the assumption that natural images have the nth Markovian property. The predicted value is obtained by using the weighted sum of causal neighbors with the weighting vector solved using the least square (LS) method. Nonetheless, due to the heavy computational load of the covariance matrix, EDP is difficult to apply. Machine learning-based methods [6,7] have higher accuracy compared to traditional predictor, they face a serious challenge in hardware implementation.

There have been studies to improve the MED [8]. However, the algorithm involves k-mean clustering, which increases time complexity compared with the original MED. We re-examined the concept of the MED and proposed three methods.

2. Proposed Methods

2.1. MED from Different View

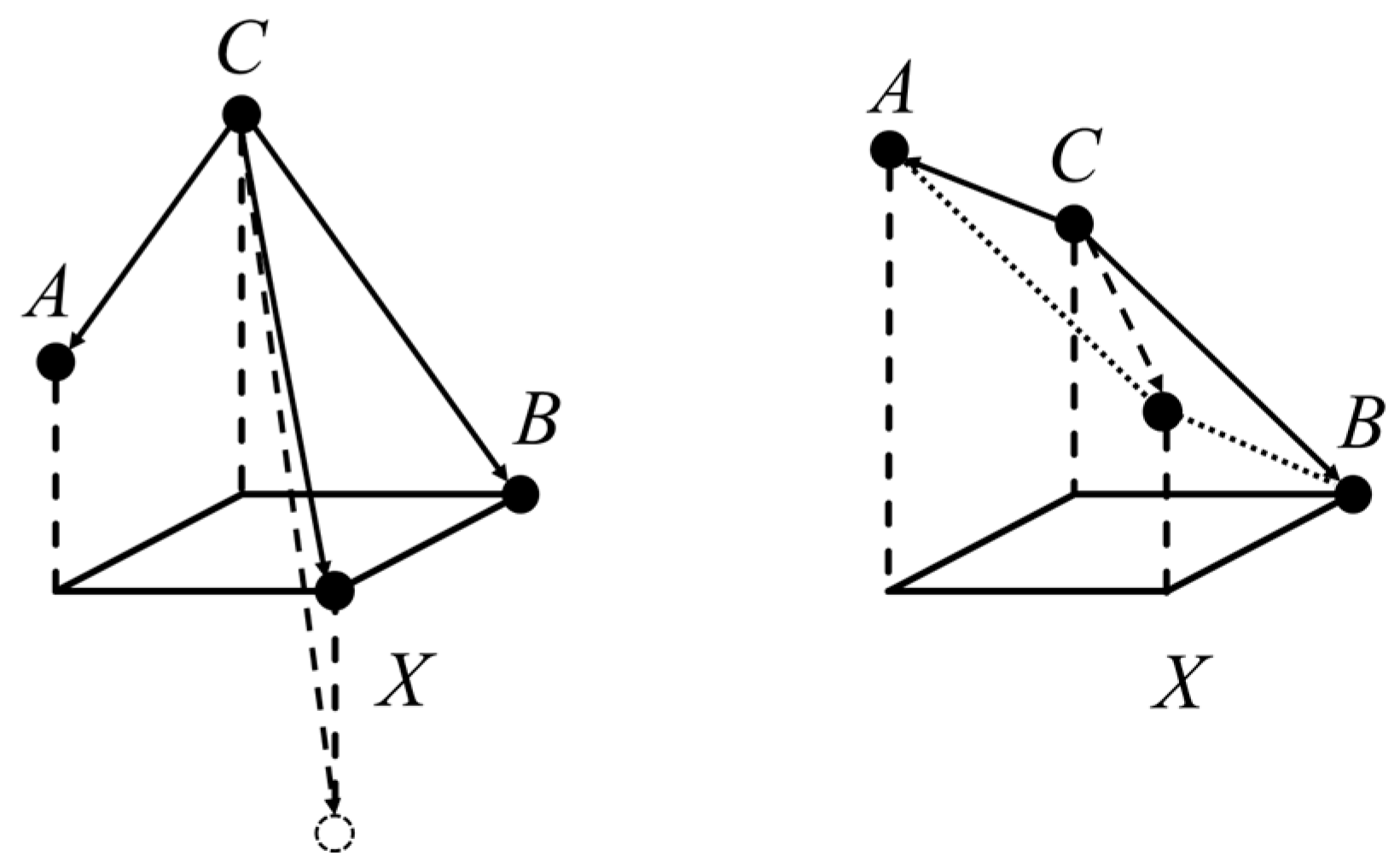
We visualized pixel values by their heights, as shown in Figure 1. The first and second conditions in (1) were treated on the left-hand side, while the third condition was the case on the right-hand side. Considering a starting point C, we used the following equation:

$$\overline{CX}=\overline{CA}+\overline{CB}$$

(2)

To predict the value X by using a vector $\overline{CX}$, the numerical value becomes A + B $-$ C, which is consistent with the third case in the MED. As for the left-hand side, we treated it as the difference of $\overline{CX}$, which is bounded by a threshold and the maximum absolute value of all differences in a 2 × 2 matrix. As A + B $-$ C represented the dotted circle on the left, the actual predicted value was bounded by the vector $\overline{CB}$. The MED assumed that there was no drastic change under the observed maximum difference in the 2 × 2 matrix.

2.2. MED Without Threshold and with a 3 × 3 Threshold

After the analysis, we explored the performance if this threshold was flexible. The first proposed method was the MED with an infinite threshold. The predicted value was A + B $-$ C for any case. The other method was to change the original 2 × 2 matrix into a 3 × 3 matrix, as shown in Figure 2. The threshold was set as the maximum of all differences between adjacent pixels including the diagonal direction, where 17 vectors were considered. The two methods encountered predicted values over 255 or under 0, while the input image had a bit depth of 8, and thus an additional conditional clause was added after to solve this problem.

2.3. Adaptive MED

Aside from the two methods, we considered the residue of causal parts. That is, the performance of the previous prediction became a factor to consider when predicting the current pixel. The predicted value was defined as shown in (3):

$$X\triangleq \left\{\begin{array}{l}result of MED+median([resA, resB, resC])\\ if sign(resA==resB==resC)\\ \\ result of MED otherwise\end{array}\right.$$

(3)

where resA, resB, and resC are the residues of A, B, and C in Figure 2. If the causal residues have positive or negative signs, the predictor underestimates or overestimates in that region. Hence, the predicted value becomes the result of the original MED added with the median of the three residues.

2.4. Vertical/Horizontal Flip

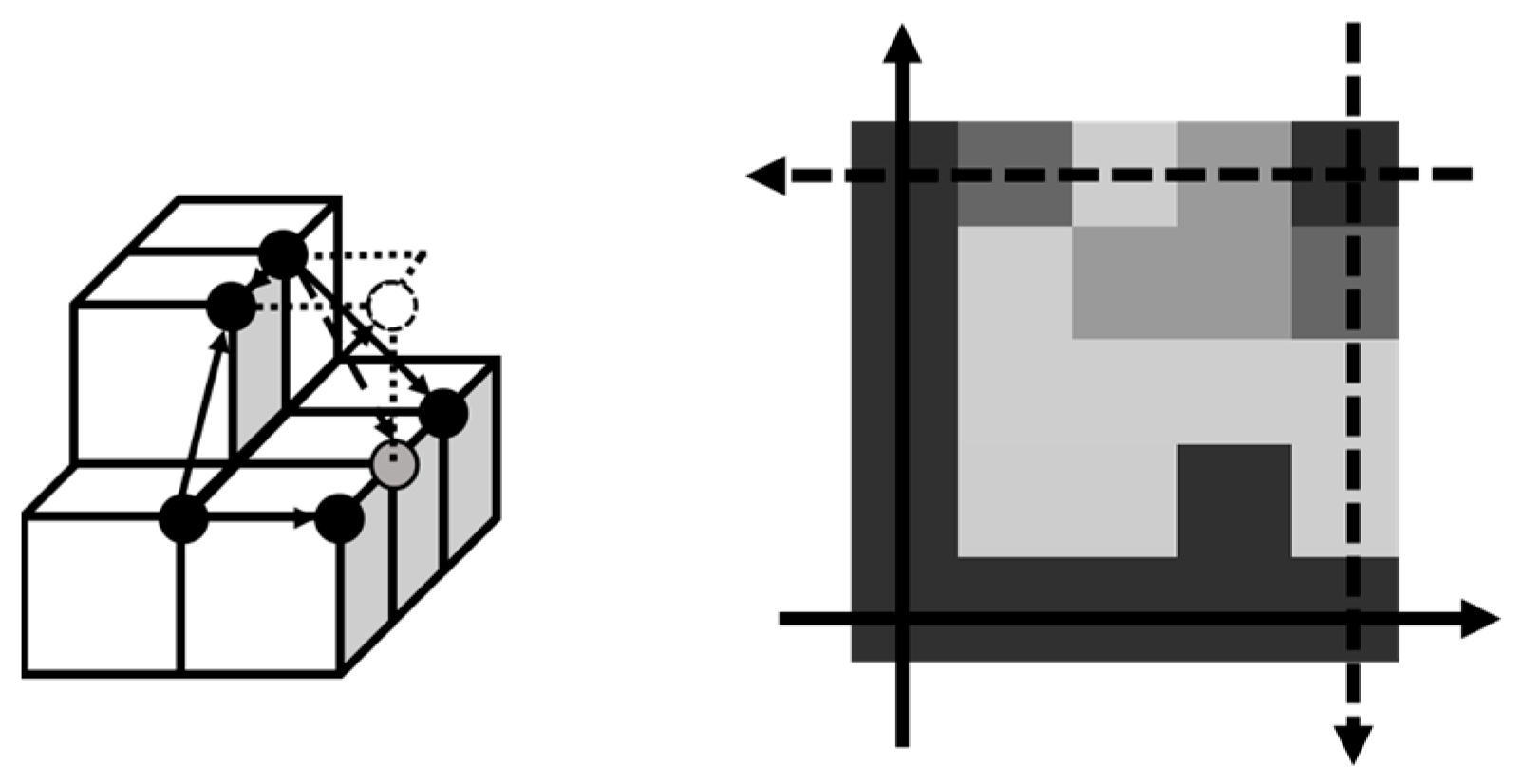
Block-based compression is popular because its parallel processing shortens the time for the encoder and decoder. We introduced a vertical and horizontal flip technique to determine if the block was vertically or horizontally flipped according to the sum of squared difference (SSD). The reason why vertical/horizontal flip improves the residue is depicted on the left side of Figure 3. Suppose the grey circle is the pixel being predicted. Based on the MED predictor, there are two different predicted values if the MED is performed by the outside and inside directions and the former one has a better predicted value.

Since the pixels at a boundary have little information for prediction, direct left or direct top are applied as predicted values. If the region is unfortunately rough at the starting point, as shown in the top-right on the right-hand side of Figure 3, residues with large values remain. If the block is flipped vertically and horizontally, the starting point is found in the bottom left. When the boundary is smoother, the residue of the direct top and direct left is mitigated, while the predicted value in the rough region is replaced by the MED.

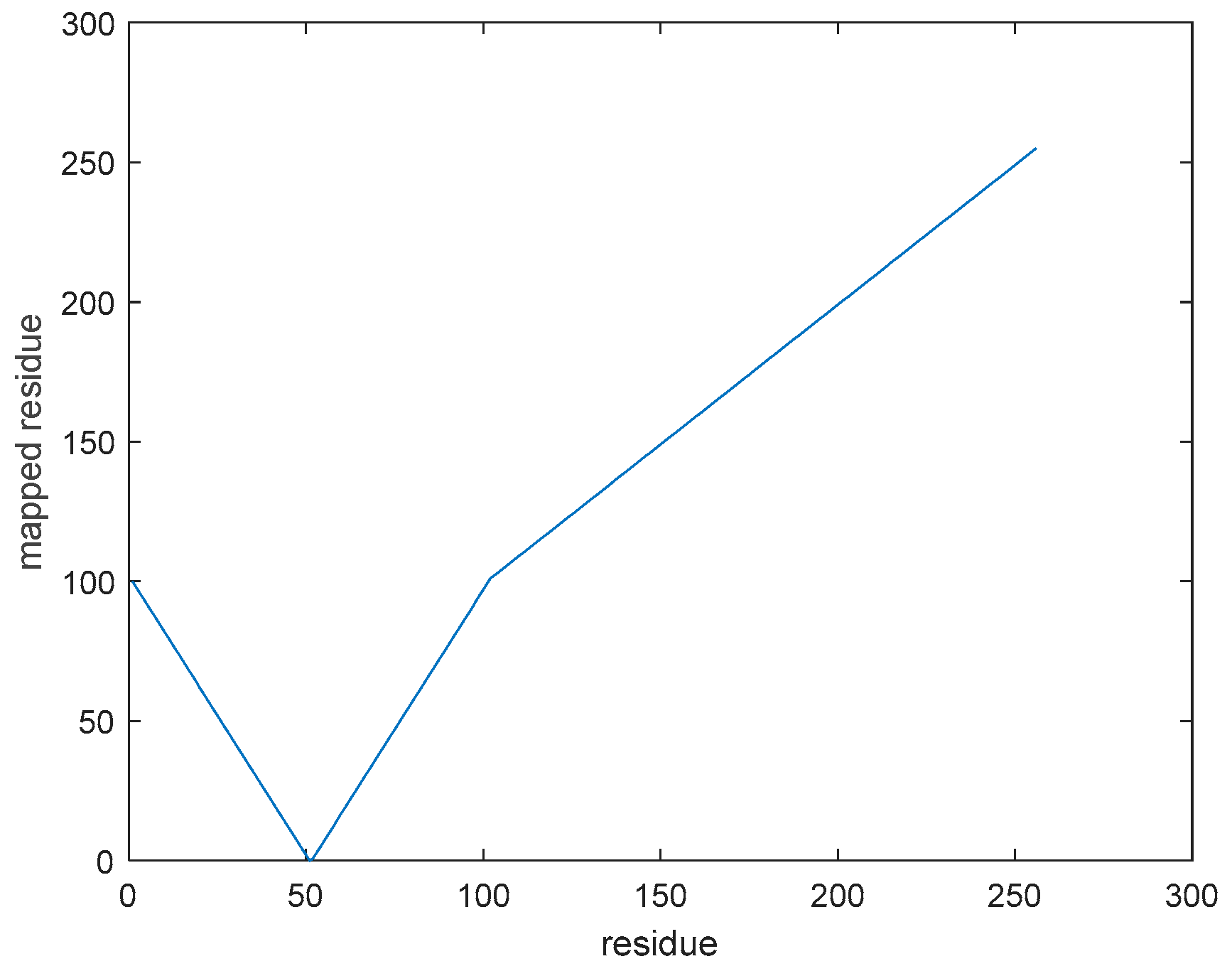
2.5. Residue Mapping

Originally, the residues were distributed on the interval [−255, 255], but little redundancy exists. That is, once the predicted value is confirmed, the residue range is located as well. For example, if the predicted value is 50, then it is impossible that the residue becomes less than −50 or more than 205. By shifting the interval [50, 205] to [100, 255], [−50, 50] can be mapped to [0, 100] by replacing their signs, as shown in Figure 4. The mathematical form used to define an anchor point is shown in (4):

$$anchor=\left\{\begin{array}{l}predict if predict\le 2^{n-1}-1\\ 2^n-predict if predict>2^{n-1}-1\end{array}\right.$$

(4)

$$mapped residue\triangleq \left\{\begin{array}{l}2\cdot \left|residue\right|\\ if residue\le 0 and \left|residue\right|\le anchor\\ \\ 2\cdot \left|residue\right|-1\\ if residue>0 and \left|residue\right|\le anchor\\ \\ \left|residue\right|+predict otherwise\end{array}\right.$$

(5)

where n is the input bit depth. By performing residue mapping, we could save the sign bit.

3. Experimental Results

We select an experimental dataset from Ref. [9], which contains 5 image categories. Each category has 65 images with a resolution from 4000 to 8000, on average, as shown in Figure 5.

Table 1. A comparison of the residual entropy of the proposed and other algorithms for full size compression.

Full Size	MED	MED Without Threshold	3 × 3 Ranged Threshold	Adaptive Prediction
mountain	4.9827	5.0320	4.9255	4.8388
capture	4.0214	4.0771	3.9514	3.8621
street	5.2816	5.4018	5.2873	5.2097
building	5.0343	5.1060	5.0068	4.9211
animal	5.1374	5.2777	5.1469	5.0726
average	4.8915	4.9789	4.8636	4.7809

,

Table 2. A comparison of the residual entropy of the proposed and other algorithms for 8 × 8 block-based compression.

8 × 8	MED	MED Without Threshold	3 × 3 Ranged Threshold	Adaptive Prediction
mountain	5.1531	5.0942	5.0779	4.9886
capture	4.2426	4.1864	4.1765	4.0661
street	5.4400	5.4395	5.4222	5.3343
building	5.2140	5.1805	5.1676	5.0801
animal	5.2903	5.3060	5.2826	5.1910
average	5.0680	5.0413	5.0254	4.9320

,

Table 3. A comparison of the residual entropy of the proposed and other algorithms for 16 × 16 block-based compression.

16 × 16	MED	MED Without Threshold	3 × 3 Ranged Threshold	Adaptive Prediction
mountain	5.0469	5.0397	5.0170	4.8927
capture	4.0995	4.0956	4.0822	3.9307
street	5.3410	5.3977	5.3736	5.2515
building	5.1040	5.1203	5.1021	4.9804
animal	5.1927	5.2683	5.2361	5.1102
average	4.9568	4.9843	4.9622	4.8331

,

Table 4. A comparison of the residual entropy of the proposed and other algorithms for 32 × 32 block-based compression.

32 × 32	MED	MED Without Threshold	3 × 3 Ranged Threshold	Adaptive Prediction
mountain	5.0084	5.0290	5.0029	4.8594
capture	4.0523	4.0775	4.0618	3.8881
street	5.3054	5.3933	5.3653	5.2246
building	5.0631	5.1067	5.0855	4.9448
animal	5.1591	5.2667	5.2298	5.0854
average	4.9177	4.9746	4.9491	4.8005

and

Table 5. A comparison of the residual entropy of the proposed and other algorithms with vertical/horizontal flip.

	MED	MED Without Threshold	3 × 3 Ranged Threshold	Adaptive Prediction
8 × 8 v flip	5.0637	5.0389	5.0223	4.9217
8 × 8 v/h flip	5.0747	5.0459	5.0295	4.9300
16 × 16 v flip	4.9464	4.9783	4.9555	4.8182
16 × 16 v/h flip	4.9480	4.9773	4.9545	4.8174
32 × 32 v flip	4.9064	4.9693	4.9432	4.7866
32 × 32 v/h flip	4.9063	4.9677	4.9415	4.7848

show the comparison results of entropy between the proposed method and original MED in full size, 8 × 8, 16 × 16, and 32 × 32. MED without threshold is inferior to MED in a larger size but outperforms MED in several categories when the block size is 8 × 8. By examining the dataset, we discovered that MED without threshold has an advantage when the input images are composed of complicated textures. For example, the peacock, leaves, and forest in Figure 5 contain complicated regions, and the MED without a threshold surpasses the MED by an entropy reduction of 0.1 on average. The performance of the 3 × 3 matrix is similar to that of the MED without a threshold. It outperforms the MED in the 8 × 8 matrix and is inferior with a larger size, but unexpectedly surpasses the MED in full size.

Adaptive prediction has the lowest entropy in every category and block size. Additionally, the result of 32 × 32 is extremely close to that of the full size, which indicates that the time spent is 32/N, determined by sacrificing a few compression rates (CRs), where N is the length of the input image with the same infinite encoder and decoder. Table 5 shows the result of the vertical flip and hybrid flip in different block sizes. The entropy is the original entropy added by the extra bits 1/(square of block size) depending on the flipped block.

If the block size is 32 × 32, the extra bpp required becomes 1/32/32 = 0.000976. The value is multiplied by 2 if the block is applied with the hybrid flip. Using only one one-direction flip is the most appropriate approach, since the trade-off between the entropy reduction and the extra bits balances the buffer to record growing residues exponentially.

4. Conclusions

We provide the other point of view on the MED to propose an improved low-complexity predictor based on the MED. While several predictors perform better than the MED only in small block sizes, the best predictor, the improved MED, outperforms the MED for all cases. In addition, a vertical/horizontal flip scheme is proposed. By spending extra bits to record the flipped block, the entropies are further reduced.