Innovative Model for Material Selection Within the Automotive Lightweight Eco-Design Field ^†

Abstract

This paper presents an innovative integrated Ashby-VIKOR model for material selection when dealing with the re-design of automotive components under a wide-spectrum range of both sustainability and design aspects. The conceived approach combines the Ashby method, which assesses mechanical properties and costs, with the VIKOR multi-criteria decision analysis, including a comprehensive model functional to assess the environmental impact of the considered automotive assets. This study also incorporates the implementation of the methodology to a literature case study (engine bracket for a C-class electric vehicle) to evaluate the robustness of the approach under varying different boundary conditions of the analysis. The results show the usefulness of the method in assessing new lightweight design solutions under an integrated structural integrity/sustainability point of view. In particular, the outcomes of the case study analysis show that significant improvements are offered by the lightweight alternative both in terms of component weight, cost efficiency and carbon footprint, identifying low-alloy steels and aluminum composites as optimal materials for this specific application.

1. Introduction

Reducing greenhouse gas (GHG) emissions has become a priority for the automotive industry, especially in Europe, where the sector is responsible for approximately 20% of total GHG emissions [1]. To meet the European Union’s ambitious target of reducing emissions by 60% by 2050 compared to 1990 levels, vehicle lightweighting has emerged as a key design scenario [2]. Studies show that a 10% reduction in vehicle weight can lead to a 5–8% improvement in fuel efficiency [3]. As a consequence, material selection definitely represents a critical aspect when designing more sustainable cars.

Lightweighting is achieved by replacing traditional materials with lighter alternatives such as advanced polymers, composites, and high-performance alloys [4], including materials suitable for additive manufacturing [5]. In view of the vast range of materials available on the market and the most diverse applications they can be applied to, selecting the most appropriate solution is, for all intents and purposes, a multicriteria challenge, often including conflicting aspects, ranging from mechanical performance to cost and environmental impact [6].

The traditional method developed by Ashby provides a valid approach for material selection when dealing with the structural integrity design aspect by addressing the mechanical profile of materials [7]. In particular, the Ashby method is effective when considering a limited number of parameters (typically two or three), but its complexity increases significantly when more factors are introduced, limiting its ability to provide a clear and unique material choice. Indeed, while the method uses performance indices that are independent of the user’s experience, these are often insufficient to make a final decision in more complex scenarios [8].

In this context, Multi-Criteria Decision Analysis (MCDA) methods are often applied to perform material selection based on individual properties such as failure load, tensile strength, and cost; in this regard, the literature provides a series of studies which are based on such multi-criteria approaches [9,10,11,12,13,14,15,16,17]. That said, while the use of MCDA methods strongly simplifies the selection process, it often fails to fully capture the specific physical phenomena relevant to the given case studies. This point certainly represents an advantage in favor of the Ashby method as it better reflects material specificities using performance indices derived from the combination of multiple physical and mechanical properties. That said, it has to be taken into account that cost considerations are often limited to raw material acquisition, thus neglecting manufacturing costs and the environmental impacts associated with the entire component life cycle, such as disposal and recycling at end of life.

In view of the abovementioned gaps identified in the existing literature, this study proposes an innovative method that combines Ashby’s approach with the Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR) MCDA technique [18] to rank materials based on performance, cost, and environmental impact, addressing both lightweighting and sustainability. By integrating these two methods, this paper provides a more comprehensive approach that considers mechanical properties, production costs, and environmental impact. This hybrid methodology represents a significant step forward in material selection for automotive design, bridging the gap between traditional processes and the growing demand for sustainable development.

2. Materials and Method

This study proposes an innovative functional methodology to select materials for automotive components, which takes into account all main critical aspects when dealing the re-design of automotive components: structural integrity, lightweighting, cost and environmental impact. The process is divided into three main phases:

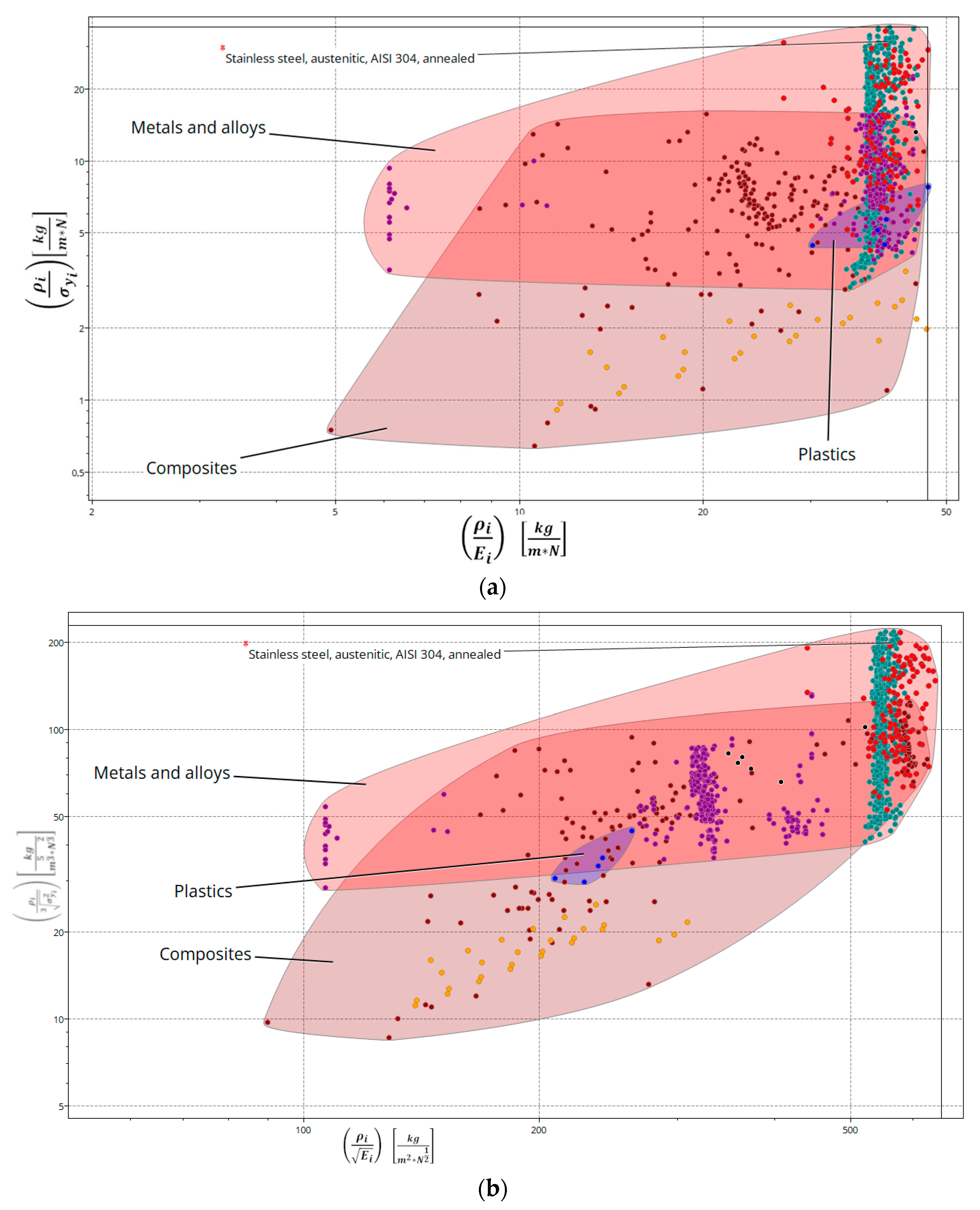
• Material selection: The method originates from the basic idea of Ashby’s approach, which uses performance indices to evaluate materials’ mechanical properties. These indices are calculated based on constraints and objectives that characterize the specific component considered. The primary goal of this work is to identify materials able to optimize design aspects (strength and stiffness) while minimizing component weight. This is accomplished by comparing a broad-spectrum of mechanical features functional to compare new material options to a reference solution by means of mechanical indices such as density, yield strength, and Young’s modulus;
• VIKOR integration: The materials selected by Ashby’s method are ranked through VIKOR’s Multi-Criteria Decision Analysis (MCDA) technique. This stage considers not only mechanical properties but also cost (derived from raw material and manufacturing costs) and environmental impact (calculated using kilograms CO₂ equivalent emissions for production, use phase and end-of-life phases). The ranking is carried out on the basis of an innovative comprehensive score that integrates the three main pillars above (design, cost sustainability, environmental sustainability);
• Sensitivity analysis: A sensitivity analysis is performed to evaluate how changes in key parameters (such as weighting factors for design, cost, and environmental impact) affect the final ranking. Such an analysis is useful to assist in evaluating the robustness of the model as well as identifying the most critical factors influencing the material selection process.

2.1. Material Selection

The description of the innovative eco-design method is performed considering a practical case study taken from a paper in the literature [19], an engine mounting bracket of a C-class commercial electric car, which is produced by Press Forming as the primary process. The component is re-designed by applying the finite element method while maintaining the original material of the bracket. The original material is AISI 304 stainless steel consisting of several sheets welded together. According to [19], the component must withstand a torque of 3 × 10⁵ N/mm, with a mass of about 8.91 kg and a maximum equivalent stress of 170 MPa.

As the bracket is very close to the electric motor, it is assumed that it does not have to endure high air temperatures, as in the case of components close to internal combustion engines. As a consequence, it is considered that the operating temperature is 70 °C, while a minimum yield strength of 170 MPa is assumed as the lower limit value. The component should be yield-resistant and stiff, but as light as possible.

As regards the selection process, the ANSYS GrantaSelector [20] software is used, based on Ashby’s method. Materials that are not suitable for the considered application are excluded a priori: single fibers, particles, ceramics, glasses (inadequate mechanical features) and honeycombs (excessive manufacturing cost for a commercial vehicle part). Considering the forces that act on the engine bracket [19], the compatible Performance Indices (PI) for this case study are the following:

$$P{I}_1={\displaystyle \frac{{\mathit{\rho }}_{\mathit{i}}}{{\mathit{E}}_{\mathit{i}}}} ;P{I}_2={\displaystyle \frac{{\mathit{\rho }}_{\mathit{i}}}{{\mathit{\sigma }}_{{\mathit{y}}_{\mathit{i}}}}} ; P{I}_3={\displaystyle \frac{{\mathit{\rho }}_{\mathit{i}}}{\sqrt{{\mathit{E}}_{\mathit{i}}}}}; P{I}_4={\displaystyle \frac{{\mathit{\rho }}_{\mathit{i}}}{\sqrt[\mathbf{3}]{{\mathit{\sigma }}_{{\mathit{y}}_{\mathit{i}}}^{\mathbf{2}}}}}$$

where ${\rho }_i$ is the material density $\left[{\displaystyle \frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^3}}\right]$, $E_i$ is the Young’s modulus [GPa], and ${\sigma }_{y_i}$ is the material yield strength $\left[\mathrm{M}\mathrm{P}\mathrm{a}\right]$. The first two indices refer to the case of tension and compression loads, and the second to the torque bending load. From these indices, the Ashby plots shown in Figure 1 are derived, which display how different material options are positioned with respect to the indices above.

To avoid selecting too many materials to be processed within the subsequent analysis with the VIKOR method, it is decided to include all materials that provide a worsening of the performance indices by no more than 15% compared to the reference material. The screening process above provides 1151 materials selected from the Granta Selector database, highlighting that the best performing materials are found to be composites, as shown in Figure 1.

2.2. Integration of Ashby/VIKOR

This section provides the integration of Ashby’s method with MCDA VIKOR, including the description of the selected indices. As reported in the literature, the VIKOR method can be affected by the type of normalization performed on the pairwise matrix, as shown in [21]. For this reason, the normalization criterion used in this paper to apply the VIKOR is described through the following equation:

$${\mathit{f}}_{\mathit{i}\mathit{l}}={\displaystyle \frac{{\mathit{x}}_{\mathit{i}\mathit{l}}}{\sqrt{{\sum }_{\mathit{i}=\mathbf{1}}^{\mathit{m}}\left({\mathit{x}}_{\mathit{i}\mathit{l}}^{\mathbf{2}}\right)}}}$$

where $x_{il}$ is the value of the l-th criterion for the i-th material, and $f_{il}$ is the value normalized.

The method then calculates two key metrics: S_i (the utility measure, representing the total group benefit) and R_i (the regret measure, reflecting the worst-case scenario for each criterion).

The final score Q_i is computed as a compromise between group utility and individual regret, based on parameter (v) that expresses the decision-maker’s preference for one of the two strategies [22].

As regards the definition of the VIKOR design indices, specific parameters are selected based on their ability to accurately reflect the trade-offs between the abovementioned conflicting criteria (mechanical performance, cost, and environmental impact). Considering that the primary goal of this study is to identify a material that provides a reduction in bracket mass, the Ashby performance indices are used to make a prediction of the component weight in all the lightweight versions considered. To define a baseline for carrying out the comparison, the reference material is also assessed according to the same PIs defined above:

$$\mathit{P}{\mathit{I}}_{\mathit{r}\mathit{e}{\mathit{f}}_{\mathbf{1}}}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}}}; \mathit{P}{\mathit{I}}_{\mathit{r}\mathit{e}{\mathit{f}}_{\mathbf{2}}}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{\sigma }}_{{\mathit{y}}_{\mathit{r}\mathit{e}\mathit{f}}}}}; \mathit{P}{\mathit{I}}_{\mathit{r}\mathit{e}{\mathit{f}}_{\mathbf{3}}}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}}{\sqrt{{\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}}}}; \mathit{P}{\mathit{I}}_{\mathit{r}\mathit{e}{\mathit{f}}_{\mathbf{4}}}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}}{\sqrt[\mathbf{3}]{{\mathit{\sigma }}_{{\mathit{y}}_{\mathit{r}\mathit{e}\mathit{f}}}^{\mathbf{2}}}}}$$

These PIs are derived from the objective functions provided below:

$${\mathit{m}}_{\mathit{r}\mathit{e}\mathit{f}}\ge \mathit{f}{\left(\mathit{F}\right)}_{\mathit{r}\mathit{e}\mathit{f}}\cdot \mathit{f}{\left(\mathit{G}\right)}_{\mathit{r}\mathit{e}\mathit{f}}\cdot \mathit{P}{\mathit{I}}_{\mathit{r}\mathit{e}\mathit{f}}$$

where f(F)_ref are the functional requirements, f(G)_ref are the component geometric parameters, and m_ref is the mass of the component. This equation can be employed for novel materials as well. By calculating the ratio of each performance index, with $f{\left(F\right)}_{ref}=f{\left(F\right)}_i$ and $f{\left(G\right)}_{ref}$ = $f{\left(G\right)}_i$, four mass ratios are obtained.

$${\left({\displaystyle \frac{{\mathit{m}}_{\mathit{i}}}{{\mathit{m}}_{\mathit{r}\mathit{e}\mathit{f}}}}\right)}_{\mathbf{1}}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{i}}{\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}{\mathit{E}}_{\mathit{i}}}};{\left({\displaystyle \frac{{\mathit{m}}_{\mathit{i}}}{{\mathit{m}}_{\mathit{r}\mathit{e}\mathit{f}}}}\right)}_{\mathbf{2}}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{i}}{\mathit{\sigma }}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}{\mathit{\sigma }}_{{\mathit{y}}_{\mathit{i}}}}};{\left({\displaystyle \frac{{\mathit{m}}_{\mathit{i}}}{{\mathit{m}}_{\mathit{r}\mathit{e}\mathit{f}}}}\right)}_{\mathbf{3}}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{i}}}{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}}}\sqrt{{\displaystyle \frac{{\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{E}}_{\mathit{i}}}}};{\left({\displaystyle \frac{{\mathit{m}}_{\mathit{i}}}{{\mathit{m}}_{\mathit{r}\mathit{e}\mathit{f}}}}\right)}_{\mathbf{4}}={\displaystyle \frac{{\mathit{\rho }}_{\mathit{i}}}{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}}}\sqrt[\mathbf{3}]{{\left({\displaystyle \frac{{\mathit{\sigma }}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{\sigma }}_{{\mathit{y}}_{\mathit{i}}}}}\right)}^{\mathbf{2}}}$$

To avoid $f{\left(F\right)}_{ref}=f{\left(F\right)}_i$ and $f{\left(G\right)}_{ref}$ = $f{\left(G\right)}_i$, the mass of the new component is obtained using a weighted average of PIs’ ratio based on the mass of the baseline component version.

$${\mathit{m}}_{\mathit{i}}={\mathit{m}}_{\mathit{r}\mathit{e}\mathit{f}}{\displaystyle \frac{{\mathit{w}}_{\mathbf{1}}\frac{{\mathit{\rho }}_{\mathit{i}}{\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}{\mathit{E}}_{\mathit{i}}}+{\mathit{w}}_{\mathbf{2}}\frac{{\mathit{\rho }}_{\mathit{i}}{\mathit{\sigma }}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}{\mathit{\sigma }}_{{\mathit{y}}_{\mathit{i}}}}+{\mathit{w}}_{\mathbf{3}}\frac{{\mathit{\rho }}_{\mathit{i}}}{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}}\sqrt{\frac{{\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{E}}_{\mathit{i}}}}+{\mathit{w}}_{\mathbf{4}}\frac{{\mathit{\rho }}_{\mathit{i}}}{{\mathit{\rho }}_{\mathit{r}\mathit{e}\mathit{f}}}\sqrt[\mathbf{3}]{{\left(\frac{{\mathit{\sigma }}_{\mathit{r}\mathit{e}\mathit{f}}}{{\mathit{\sigma }}_{{\mathit{y}}_{\mathit{i}}}}\right)}^{\mathbf{2}}}}{{\sum }_{\mathit{j}=\mathbf{1}}^{\mathbf{4}}{\mathit{w}}_{\mathit{j}}}}$$

where $w_j$ are correction weights that consider the type of load, geometry and performance index.

This provides the first selection criterion (mass), which is considered in the application of VIKOR. The second selection criterion is the component cost, which is evaluated through the following equation based on [8]:

$${\mathit{E}\mathit{u}\mathit{r}}_{\mathit{i}\mathit{k}}={\mathit{m}}_{\mathit{i}}{\displaystyle \frac{{\mathit{C}}_{{\mathit{m}}_{\mathit{i}}}}{\mathbf{1}-{\mathit{f}}_{\mathit{k}}}}+\left({\displaystyle \frac{{\mathit{C}}_{{\mathit{t}}_{\mathit{k}}}}{\mathit{n}}}\right)\mathit{i}\mathit{n}\mathit{t}\left({\displaystyle \frac{\mathit{n}}{{\mathit{n}}_{{\mathit{t}}_{\mathit{k}}}}}+\mathbf{0.51}\right)+{\displaystyle \frac{\mathbf{1}}{{\dot{\mathit{n}}}_{\mathit{k}}}}\left({\displaystyle \frac{{\mathit{C}}_{{\mathit{c}}_{\mathit{k}}}}{{\mathit{L}}_{\mathit{k}}\ast {\mathit{t}}_{{\mathit{w}\mathit{o}}_{\mathit{k}}}}}\right){\left(\mathbf{1}+\mathit{d}\right)}^{{\mathit{t}}_{{\mathit{w}\mathit{o}}_{\mathit{k}}}}+{\displaystyle \frac{{\dot{\mathit{C}}}_{\mathit{o}\mathit{h}}}{{\dot{\mathit{n}}}_{\mathit{k}}}}$$

where k is k-th industrial process, $C_{m_i}$ is the cost of the raw material [EUR/kg], $f_k$ is the scrap fraction—the fraction of the starting material that ends up as sprues, risers, turnings, rejects or waste [-]$—C_{t_k}$ is the cost of tooling when it needs to be replaced [EUR], n is the batch size considered for the production of the component [-], $n_{t_k}$ is the number of units that a set of tooling can produce before it has to be replaced [-], ${\dot{n}}_k$ is the production rate of the k-th process [1/h], $C_{c_k}$ is the Capital Cost of Equipment [EUR], $L_k$ is the Load Factor, the fraction of time for which the equipment is productive [-], $t_{{wo}_k}$ is the capital write-off time [years], d is the discount rate [-], and ${\dot{C}}_{oh}$ is the overhead rate [EUR/h].

This model considers the cost not only of raw material but also of the primary process, including the expenditure for the initial investment of the production line, the indirect costs and the cost for tool replacement. The values for parameters ${\dot{C}}_{oh}, t_{w{o}_k}, L_k, d$ are taken from the default settings provided by Granta Selector software, which report that such parameters are constant for each industrial process (${\dot{C}}_{oh}={\displaystyle \frac{150\mathrm{€}}{\mathrm{h}\mathrm{r}}},{t_{w{o}_k}=5 \mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s},L}_k$= 0.5, $d$ = 0.05). Parameter n is assumed to be 100,000 units annually since it is assumed to consider a large-scale production for an electric commercial vehicle.

Given the bracket specifications and geometry, only a subset of the processes available in the Granta database are selected (i.e., only those processes that are compatible with the component and the materials under consideration). As not all materials can be produced by all industrial processes (due to technological constraints, material properties and geometry reasons), a selection of processes is selected, which is provided in

Table 1. Industrial processes chosen for this case study (data provided by Granta Selector Database [19]).

Industrial Processes	${\mathit{C}}_{{\mathit{t}}_{\mathit{k}}}$	${\mathit{C}}_{{\mathit{C}}_{\mathit{k}}}$	$1-{\mathit{f}}_{\mathit{k}}$	${\mathit{n}}_{{\mathit{t}}_{\mathit{k}}}$	${\dot{\mathit{n}}}_{\mathit{k}}$
Binder Jetting	0.05	361,000	0.98	22.4	22.4
Cold Isostatic Pressing (CIP)	1470	141,000	0.99	31.6	31.6
Evaporative pattern casting, automated	2980	23,086	0.49	31.62	31.62
Ferro die casting	44,500	393,000	0.8	54.8	54.8
Gravity die casting	10,500	35,200	0.69	15.8	15.8
Green sand casting, automated	2150	39,300	0.63	77.5	77.5
Investment casting, automated (lost wax process)	6810	39,300	0.82	44.7	44.7
Press forming	78,600	278,000	0.75	77.5	77.5
Replicast casting	5560	21,500	0.69	22.4	22.4
Shell casting	3930	5560	0.49	15.81	15.81
Squeeze casting	22,200	393,000	0.93	30	30

. This way, it is possible to investigate the entire set of processes and technologies through which a material can be actually produced. Using this approach, the number of possible solutions increases from 1151 (when considering only material) to 1850 (when considering the combination between material and industrial process).

The third index used in the analysis takes into account the environmental impact of the component in terms of kilograms of CO₂ equivalent. Compared to the Ashby model, which only considers the environmental impact of primary material extraction, the life cycle investigation is extended to use and end-of-life phases by means of the Climate Change index CC_ik.

According to [23,24], CC_ik index is calculated using the following equation:

$$\mathit{C}{\mathit{C}}_{\mathit{i}\mathit{k}}={\mathit{m}}_{\mathit{i}}\left({\displaystyle \frac{\mathbf{1}}{\mathbf{1}-{\mathit{f}}_{\mathit{k}}}}\ast \mathit{C}{{\mathit{O}}_{\mathbf{2}}}_{\mathit{i}}+\mathit{I}\mathit{R}\mathit{V}\ast \mathit{k}\mathit{m}+{\displaystyle \frac{\mathit{C}{\mathit{C}}_{\mathit{E}\mathit{o}{\mathit{L}}_{\mathit{i}}}}{{\mathit{m}}_{\mathit{i}}}}\right)$$

where $\mathit{C}{{\mathit{O}}_{\mathbf{2}}}_{\mathit{i}}$ is the CO_2eq due to extraction of 1 kg of the i-th material and it is taken from GrantaSelector [20], km is the vehicle use stage, which is assumed to coincide with the mileage distance travelled during component operation (assumed 200,000 km) [km], IRV is the Impact Reduction Value, defined as the CC caused by the production of 1 kWh electricity consumed by the vehicle on which the component is mounted $\left[{\displaystyle \frac{\mathit{k}\mathit{g}\mathit{C}{\mathit{O}}_{\mathbf{2}}\mathit{e}\mathit{q}}{\mathbf{100}\mathit{k}\mathit{m}\ast \mathbf{100}\mathit{k}\mathit{g}}}\right]$, and $\mathit{C}{{\mathit{C}}_{\mathit{E}\mathit{o}\mathit{L}}}_{\mathit{i}}$ is the end-of-life index, which takes into account the following phases: component disassembly, component shredding, separation of component shredded material, recycling of separated material if it is possible, incineration with energy recovery of separated material if it is possible, and disposal.

2.3. Sensitivity Analysis

The literature shows that changing criteria weights in MCDA methods can lead to a variation in the results obtained. As a consequence, it is decided to carry out a sensitivity analyses of VIKOR results with the chosen indices to see what results could be obtained depending on the choice of one design scenario or another.

Table 2. Strategies studied. Columns from left to right: design scenario name, weight relative to ratio ${\displaystyle \frac{{\rho }_i{E}_{ref}}{{\rho }_{ref}{E}_i}}$ for mass calculation, weight relative to ratio ${\displaystyle \frac{{\rho }_i{\sigma }_{ref}}{{\rho }_{ref}{\sigma }_{y_i}}}$ for mass calculation, weight relative to ratio ${\displaystyle \frac{{\rho }_i}{{\rho }_{ref}}} \sqrt{{\displaystyle \frac{E_{ref}}{E_i}}}$ for mass calculation, weight relative to ratio ${\displaystyle \frac{{\rho }_i}{{\rho }_{ref}}}\sqrt[3]{{\left({\displaystyle \frac{{\sigma }_{ref}}{{\sigma }_{y_i}}}\right)}^2}$ for mass calculation, weight relative to $m_{ik}$ for VIKOR model, weight relative to ${€}_{ik}$ for VIKOR model, weight relative to ${CC}_{ik}$ for VIKOR model, selected industrial process, selected material family.

Design Scenario	${\mathit{w}}_1$	${\mathit{w}}_2$	${\mathit{w}}_3$	${\mathit{w}}_4$	$\mathbf{Weight} {\mathit{m}}_{\mathit{i}\mathit{k}}$	$\mathbf{Weight} {\mathit{E}\mathit{u}\mathit{r}}_{\mathit{i}\mathit{k}}$	$\mathbf{Weight} {\mathit{C}\mathit{C}}_{\mathit{i}\mathit{k}}$	Industrial Process	Family Material
General Design	1	1	1	1	1	1	1	All	All
Yield Design	0	1	0	1	1	1	1	All	All
Wrought Design	1	1	1	1	1	1	1	Press Forming	Compatible

shows the weights for each design scenario adopted.

${\mathit{w}}_{\mathbf{1}}{\mathit{w}}_{\mathbf{2}}{\mathit{w}}_{\mathbf{3}}{\mathit{w}}_{\mathbf{4}}$ the title of the columns refers to weights that are changed: the first column provides the name of the design scenario, the second to fifth columns provide the weights related to calculation of component mass, the sixth to eighth columns provide the weights related to mass, cost and environmental impact indices in the use of VIKOR, and the last two columns provide the industrial processes and material families selected for the specific design scenario.

The first design scenario, General Design, shows that all weights are set to one and the entire set of available processes and materials is considered. The second design scenario, Yield Design, shows that weights of stiffness and Young’s modulus are set to zero. The third design scenario is based on the assumption of maintaining the same primary manufacturing process of the baseline solution (press forming).

As $w_j$ weights vary based on relative importance of various selection criteria, different results can be obtained if such criteria are changed, not only in terms of component mass, but also in terms of cost and environmental impact. For this reason, some cut-off rules are included to disregard certain results that would be unsuitable for the chosen case study. These cut-off rules are applied before proceeding with the VIKOR analysis of the three design scenarios adopted. The first constraint concerns component mass: as the main target is reducing component mass, all the selected design solutions must verify the following inequality:

$$m_{ref}-m_i>0$$

The second constraint is the component cost: given that this case study refers to a C-class electric vehicle, it is not possible to assume very-high-performance materials because of their too high economic expenditure. So, it is assumed that all selected solutions must also verify the second inequality:

$${\displaystyle \frac{{Eur}_{ik}-{Eur}_{ref}}{m_{ref}-m_i}}<10 \left[{\displaystyle \frac{€}{kg}}\right]$$

The first term in the previous Equation is defined as DeltaEuroKilo (DEK), and it describes the maximum additional cost per kilogram saved. For the bracket component a value of 10 EUR/kg is assumed to be acceptable.

3. Results and Discussion

This section presents the results of the sensitivity analysis. Tables regarding the sensitivity analysis are reported in Appendix A, which provide the top twenty solutions ranked according to the VIKOR method for each design scenario considered. The columns in the tables provide the following data: position in the ranking, description of solution (expressed as material/primary process combination), component mass, total cost of component, cost of raw material, DEK, total environmental impact, environmental impact of raw material acquisition, environmental impact of use stage, and individual Qi scores.

Table A1. Result of GD scenario: $w_1=1$, $w_2=1$, $w_3=1$, $w_4=1$, $weight m_{ik}=1$, $weight {€}_{ik}=1$, $weight C{C}_{ik}=1$, Industrial Process = all, Family material = all.

Ranking	Solution (Material + Primary Process)	${\mathit{m}}_{\mathit{i}}$ $\left[\mathbf{k}\mathbf{g}\right]$	${\mathit{E}\mathit{u}\mathit{r}}_{\mathit{i}\mathit{k}}$ [Eur]	Raw Material [Eur]	DEK [Eur/kg]	$\mathit{C}{\mathit{C}}_{\mathit{i}\mathit{k}}$ [kgCO2eq]	$\mathit{C}{\mathit{C}}_{\mathit{R}\mathit{a}{\mathit{w}}_{\mathit{i}\mathit{k}}}$ [kgCO2eq]	$\mathit{C}{{\mathit{C}}_{\mathit{U}\mathit{s}\mathit{e}}}_{\mathit{i}\mathit{k}}$ Only Use Phase [kgCO2eq]	${\mathit{Q}}_{\mathit{i}}$
	Ref: Stainless Steel Austenitic AISI 304 Annealed–Press Forming	REF: 8.91	REF: 67	REF: 63	REF: 0	REF: 105	REF: 68	REF: 49
1	Duralcan Al-20SiC (p) cast (F3K20S).—Squeeze casting	3.81	35	28	−6	70	49	21	0.0605
2	Duralcan Al-20SiC (p) cast (F3S20S).—Squeeze casting	3.90	35	28	−6	73	51	22	0.0755
3	Duralcan Al-20Al2O3 (p) (W2A20A-T6).—CIP	3.99	37	27	−6	66	43	22	0.0779
4	Duralcan Al-20Al2O3 (p) (W6A20A-T6).—CIP	4.10	37	28	−6	68	45	23	0.0949
5	Low-alloy steel, AISI 9255, oil quenched and tempered at 205 °C.—Press Forming	4.98	13	9	−14	40	16	25	0.0961
6	Duralcan Al-15Al2O3 (p) (W2A15A-T6).—CIP	4.11	37	28	−6	69	46	23	0.0970
7	Aluminum, 2024, T8510/T8511.—Press Forming	4.32	23	20	−9	88	72	16	0.1041
8	Aluminum, 2024, T861.—Press Forming	4.33	23	20	−9	88	72	16	0.1055
9	Low-alloy steel, AISI 9255, oil quenched and tempered at 315 °C.—Press Forming	5.07	13	9	−14	41	16	25	0.1079
10	Duralcan Al-10SiC (p) cast (F3K10S).—Squeeze casting	4.11	37	30	−6	79	55	23	0.1085
11	Duralcan Al-20Al2O3 (p) (W2A20A-T6).—Press Forming	3.99	39	36	−6	80	58	22	0.1104
12	Aluminum, 5182, H19.—Press Forming	4.34	22	19	−10	91	75	16	0.1111
13	Low-alloy steel, AISI 5160, oil quenched and tempered at 205 °C.—Press Forming	5.10	13	9	−14	41	16	26	0.1116
14	Low-alloy steel, AISI 5140, oil quenched and tempered at 205 °C.—Press Forming	5.11	13	9	−14	42	16	26	0.1124
15	Low-alloy steel, AISI 5160, oil quenched and tempered at 315 °C.—Press Forming	5.11	13	9	−14	42	16	26	0.1127
16	Aluminum, 2024, T851.—Press Forming	4.37	24	20	−9	89	73	16	0.1127
17	Low-alloy steel, AISI 4140, oil quenched and tempered at 205 °C.—Press Forming	5.12	14	10	−14	42	16	26	0.1151
18	Aluminum, 2024, T81.—Press Forming	4.40	24	20	−10	89	73	17	0.1160
19	Low-alloy steel, AISI 8650, oil quenched and tempered at 205 °C.—Press Forming	5.12	14	11	−14	42	16	26	0.1164
20	Aluminum, 2014, T6510.—Press Forming	4.42	24	20	−10	89	72	17	0.1171

shows the results obtained in the GD design scenario. In this case, 1372 different solutions are rejected. The data show a clear dominance of aluminum metal matrix composites (AMCs), which appear in the first four positions of the ranking. These materials (produced by squeeze casting or cold isostatic pressing) offer a favorable balance between low mass, reasonable cost and reduced carbon footprint. Component mass is found to be between 3.8 and 4.1 kg, against a mass of the reference solution of 8.91 kg. Low-alloy steels, including AISI grades 9255, 5160, 5140, 4140 and 8650, also feature prominently in the rankings, albeit slightly lower than AMCs. These steels are processed by press forming and undergo heat treatments such as oil quenching and tempering at various temperatures. Although they have a higher mass (around 5 kg), these solutions offer significant cost advantages, with a total cost of about EUR 14, which is significantly lower than the costs associated with both aluminum alloys and composite materials (in the range of EUR 20–40) and the cost associated with the reference material (EUR 67). At the same time, these material options are also environmentally competitive, with a lower overall carbon footprint (around 40 to 42 kgCO₂eq, against 66 to 73 kgCO₂eq of AMCs and 105 kgCO₂eq of AISI 304). High-strength aluminum alloys (such as 2024 and 2014 series in various tempers) appear in the ranking but they are generally positioned lower than both AMCs and low-alloy steels. While these aluminum alloys benefit from a low mass (around 4.3 to 4.4 kg), they involve higher costs, with total expenses between EUR 22 and 24; the carbon footprint is also higher (approximately 88 to 91 kg CO₂ eq), which worsens their overall ranking despite the advantage of reduced weight.

Table A2. Result of YD scenario: $w_1=0$, $w_2=1$, $w_3=0$, $w_4=1$, $weight m_{ik}=1$, $weight {€}_{ik}=1$, $weight C{C}_{ik}=1$, Industrial Process = all, Family material = all.

Ranking	Solution (Material + Primary Process)	${\mathit{m}}_{\mathit{i}}$ [kg]	${\mathit{E}\mathit{u}\mathit{r}}_{\mathit{i}\mathit{k}}$ [Eur]	Raw Material [Eur]	DEK [Eur/kg]	$\mathit{C}{\mathit{C}}_{\mathit{i}\mathit{k}}$ [kgCO2eq]	$\mathit{C}{\mathit{C}}_{\mathit{R}\mathit{a}{\mathit{w}}_{\mathit{i}\mathit{k}}}$ [kgCO2eq]	$\mathit{C}{{\mathit{C}}_{\mathit{U}\mathit{s}\mathit{e}}}_{\mathit{i}\mathit{k}}$ Only Use Phase [kgCO2eq]	${\mathit{Q}}_{\mathit{i}}$
	Ref: Stainless Steel Austenitic AISI 304 Annealed–Press Forming	REF: 8.91	REF: 67	REF: 63	REF: 0	REF: 105	REF: 68	REF: 49
1	Low-alloy steel, AISI 9255, oil quenched and tempered at 205 °C.—Press Forming	1.64	7	3	−8	13	5	8	0.0057
2	Stainless steel, martensitic, AISI 440C, tempered at 316 °C.—Press Forming	1.72	8	4	−8	18	10	8	0.0126
3	Stainless steel, martensitic, AISI 440C, tempered at 316 °C.—Binder Jetting	1.72	11	3	−8	15	8	8	0.0132
4	Low-alloy steel, AISI 5160, oil quenched and tempered at 205 °C.—Press Forming	1.82	7	3	−8	15	6	9	0.0135
5	Low-alloy steel, AISI 9255, oil quenched and tempered at 315 °C.—Press Forming	1.82	7	3	−8	15	6	9	0.0135
6	Stainless steel, martensitic, AISI 440B, tempered at 316 °C.—Press Forming	1.75	8	4	−8	18	10	8	0.0139
7	Low-alloy steel, AISI 50B60, oil quenched and tempered at 315 °C.—Press Forming	1.83	7	3	−8	15	6	9	0.0142
8	Low-alloy steel, AISI 5160, oil quenched and tempered at 315 °C.—Press Forming	1.83	7	3	−8	15	6	9	0.0142
9	Stainless steel, martensitic, AISI 440B, tempered at 316 °C.—Binder Jetting	1.75	11	3	−8	16	8	8	0.0145
10	Low-alloy steel, AISI 5150, oil quenched and tempered at 205 °C.—Press Forming	1.87	7	3	−8	15	6	9	0.0157
11	Low-alloy steel, AISI 4150, oil quenched and tempered at 205 °C.—Press Forming	1.87	7	4	−8	15	6	9	0.0158
12	Low-alloy steel, AISI 81B45, oil quenched and tempered at 205 °C.—Press Forming	1.87	7	4	−8	15	6	9	0.0159
13	Aluminum, 7068, T6511.—Press Forming	1.38	16	12	−7	28	22	5	0.0178
14	Low-alloy steel, 300M (high carbon), quenched and tempered.—Press Forming	1.91	9	5	−8	15	6	10	0.0184
15	Low-alloy steel, AISI 8640, oil quenched and tempered at 205 °C.—Press Forming	1.92	8	4	−8	16	6	10	0.0185
16	Low-alloy steel, AISI 8650, oil quenched and tempered at 205 °C.—Press Forming	1.92	8	4	−8	16	6	10	0.0185
17	Low-alloy steel, AISI 4340, oil quenched and tempered at 205 °C.—Press Forming	1.91	8	5	−8	16	6	10	0.0185
18	Low-alloy steel, AISI 4042, oil quenched and tempered at 205 °C.—Press Forming	1.93	7	4	−8	16	6	10	0.0187
19	Low-alloy steel, AISI 8740, oil quenched and tempered at 205 °C.—Press Forming	1.93	8	4	−8	16	6	10	0.0189
20	Low-alloy steel, AISI 6150, oil quenched and tempered at 205 °C.—Press Forming	1.90	7	4	−8	18	9	9	0.0190

shows the results obtained in the YD design scenario. The data reveal that the highest-ranked materials are predominantly low-alloy steels (such as AISI 9255, 5160 and 5150) processed by press forming and heat-treated by oil quenching and tempering at various temperatures. Martensitic stainless steels (such as AISI 440C and 440B) also feature prominently, processed by press-forming and binder jetting. Despite the higher density of the steels above compared to other lighter materials (i.e., aluminum alloys), the calculated mass values are remarkably lower (in the range of 1.6–1.9 kg), thus resulting in a mass saving of about 7.3 kg compared to the baseline. This is due to the fact that the YD does not consider the elasticity modulus; so, materials with a high yield resistance have a clear advantage in the assessment. Compared to the reference material, the low-alloy steels not only achieve reduced component masses, but also offer significant cost savings and a lower carbon footprint (the cost ranges from EUR 7 to 9, significantly lower than the reference cost of the reference solution of EUR 67). CC_ik is also significantly lower (between 13 and 18 kgCO₂eq compared to 105 kgCO₂eq of the baseline). The DEK values are negative (around −EUR 8 per kilogram), due to the lower cost per unit mass of these materials. Such a cost saving, in combination with the lower environmental impact, makes these options highly attractive from both economic and sustainability points of view. Aluminum 7068 T6511 is in 13th place. This high-strength aluminum alloy provides a component mass of about 1.4 kg, the lowest of the top 20 materials, due to its low density and high yield strength. That said, there is a trade-off between mass reduction and economic/environmental factors due to higher component cost (EUR 16) and CC_ik index (28 kgCO₂eq).

Table A3. Result of Wrought Design scenario: $w_2=1$, $w_3=1$, $w_4=1$, $weight m_{ik}=1$, $weight {€}_{ik}=1$, $weight C{C}_{ik}=1$, Industrial Process = Press Forming, Family material = Compatible.

Ranking	Solution (Material + Primary Process)	${\mathit{m}}_{\mathit{i}}$ [kg]	${\mathit{E}\mathit{u}\mathit{r}}_{\mathit{i}\mathit{k}}$ [Eur]	Raw Material [Eur]	DEK [Eur/kg]	$\mathit{C}{\mathit{C}}_{\mathit{i}\mathit{k}}$ [kgCO2eq]	$\mathit{C}{\mathit{C}}_{\mathit{R}\mathit{a}{\mathit{w}}_{\mathit{i}\mathit{k}}}$ [kgCO2eq]	$\mathit{C}{{\mathit{C}}_{\mathit{U}\mathit{s}\mathit{e}}}_{\mathit{i}\mathit{k}}$ Only Use Phase [kgCO2eq]	${\mathit{Q}}_{\mathit{i}}$
	Ref: Stainless Steel Austenitic AISI 304 Annealed–Press Forming	REF: 8.91	REF: 67	REF: 63	REF: 0	REF: 105	REF: 68	REF: 49
1	Low-alloy steel, AISI 9255, oil quenched and tempered at 205 °C.—Press Forming	4.98	13	9	−14	40	16	25	0.0000
2	Low-alloy steel, AISI 9255, oil quenched and tempered at 315 °C.—Press Forming	5.07	13	9	−14	41	16	25	0.0161
3	Low-alloy steel, AISI 5160, oil quenched and tempered at 205 °C.—Press Forming	5.10	13	9	−14	41	16	26	0.0210
4	Low-alloy steel, AISI 5140, oil quenched and tempered at 205 °C.—Press Forming	5.11	13	9	−14	42	16	26	0.0221
5	Low-alloy steel, AISI 5160, oil quenched and tempered at 315 °C.—Press Forming	5.11	13	9	−14	42	16	26	0.0225
6	Low-alloy steel, AISI 4140, oil quenched and tempered at 205 °C.—Press Forming	5.12	14	10	−14	42	16	26	0.0259
7	Low-alloy steel, AISI 8650, oil quenched and tempered at 205 °C.—Press Forming	5.12	14	11	−14	42	16	26	0.0279
8	Low-alloy steel, AISI 50B60, oil quenched and tempered at 315 °C.—Press Forming	5.16	13	9	−14	42	16	26	0.0306
9	Low-alloy steel, AISI 5150, oil quenched and tempered at 205 °C.—Press Forming	5.17	13	9	−14	42	16	26	0.0336
10	Low-alloy steel, AISI 4150, oil quenched and tempered at 205 °C.—Press Forming	5.17	14	10	−14	42	16	26	0.0348
11	Low-alloy steel, AISI 81B45, oil quenched and tempered at 205 °C.—Press Forming	5.17	14	10	−14	42	16	26	0.0353
12	Low-alloy steel, AISI 94B30, oil quenched and tempered at 205 °C.—Press Forming	5.18	14	10	−14	42	16	26	0.0376
13	Low-alloy steel, AISI 4340, oil quenched and tempered at 205 °C.—Press Forming	5.15	17	13	−13	42	16	26	0.0380
14	Low-alloy steel, AISI 8650, oil quenched and tempered at 315 °C.—Press Forming	5.18	15	11	−14	42	16	26	0.0384
15	Low-alloy steel, AISI 5140, oil quenched and tempered at 315 °C.—Press Forming	5.21	13	9	−14	42	16	26	0.0400
16	Low-alloy steel, AISI 4042, oil quenched and tempered at 205 °C.—Press Forming	5.20	14	10	−14	42	16	26	0.0404
17	Low-alloy steel, AISI 9255, oil quenched and tempered at 425 °C.—Press Forming	5.21	13	10	−14	42	16	26	0.0414
18	Low-alloy steel, AISI 8640, oil quenched and tempered at 205 °C.—Press Forming	5.20	15	11	−14	42	16	26	0.0415
19	Carbon steel, AISI 1340, oil quenched and tempered at 205 °C.—Press Forming	5.22	13	9	−15	42	16	26	0.0424
20	Low-alloy steel, AISI 8740, oil quenched and tempered at 205 °C.—Press Forming	5.20	15	11	−14	42	16	26	0.0425

shows the results obtained in the Wrought design scenario. Low-alloy steels (such as AISI 9255, AISI 5160 and AISI 5140), heat-treated and extruded, emerge as the optimum solutions. The carbon footprints of the top materials are significantly lower than the reference material, ranging from 40 to 42 kgCO₂-eq, compared to the baseline of 105 kgCO₂eq. The first-ranked material is, as in the YD design scenario, low-alloy steel, AISI 9255, oil quenched and tempered at 205 °C, with a calculated component mass of around 5 kg. This value is higher than the mass in Table A2: the explanation for this is that the Young modulus is considered in the m_i calculation. The cost of such a solution is EUR 13, significantly lower than the reference cost (EUR 67), and it involves a carbon footprint of 40 kgCO₂eq compared to 105 kg CO₂eq of the reference. The DEK is −14 EUR/kg, indicating a significant cost saving per kilogram. The subsequent positions are occupied by similar low-alloy steels, such as AISI 9255 quenched and tempered at 315 °C, AISI 5160, AISI 5140 and AISI 4140, all processed and heat-treated. The consistency of these materials in the top rankings underlines their favorable combination of mechanical properties, cost effectiveness and environmental performance. Cost efficiency is a major advantage of these low-alloy steels. The costs of the top-ranked materials range from EUR 13 to 17, well below the reference cost. The negative DEK values (ranging from −14 to −13EUR/kg) highlight the economic benefits of selecting these materials over the reference. The carbon footprint of the top materials is significantly lower than that of the baseline, ranging from 40 to 42 kgCO₂eq compared to the reference (105 kgCO₂eq).

4. Conclusions

This article presents an innovative integrated Ashby/VIKOR model for material selection in the field of automotive eco-design. First, the methodology conceived is described, and, taking a specific re-design case study from the literature, it is applied and validated from a practical point of view. The chosen case study is an engine bracket support of a C-class electric vehicle, which, in the baseline design, is made of AISI 304 Stainless Steel manufactured through the press forming primary process. The results are calculated for three different design scenarios (General Design, Yield Design and Wrought Design), and a sensitivity analysis is conducted by changing the weight criteria of the integrated Ashby/VIKOR model.

As regards the case study results, the alternative materials allow for the achievement of significant mass reduction, ranging from approximately 1.64 to 5.25 kg, against a mass of 8.9 kg for the baseline component. The cost of the first 10 lightweight solutions in all design scenarios is significantly lower than that of the baseline, with a reduction in the range of 50–80%. The results show that lightweight solutions also provide advantages when considering the environmental profile, with CC decreases in the range of 30–87% kgCO₂-eq. The best material found, ranked first in 2 out of 3 design scenarios, is found to be a low-alloy steel, AISI 9255, oil quenched and tempered at 205 °C, produced by press forming. With this material, the component is expected to weigh a minimum of around 1.6 kg, with a cost of EUR 7 and an environmental impact of 13 kgCO₂-eq.

In the light of the case study results, the main potentiality of the refined method is two-fold. On the one hand, it allows for the assessment of different material options, taking into account both design and structural integrity issues at the same time, as well as economic and environmental sustainability. On the other hand, the methodology enables an investigation of a wide range of possible material alternatives, taking into account not only the structural performances and life-cycle profile of the materials themselves, but also the effect that manufacturing technologies have on such a multidisciplinary assessment approach.