Enhancing Voltage and Power Output Through the Structural Optimization of Coil–Magnet Transducers in Electromagnetic Vibration Energy Harvesters †
Abstract
1. Introduction
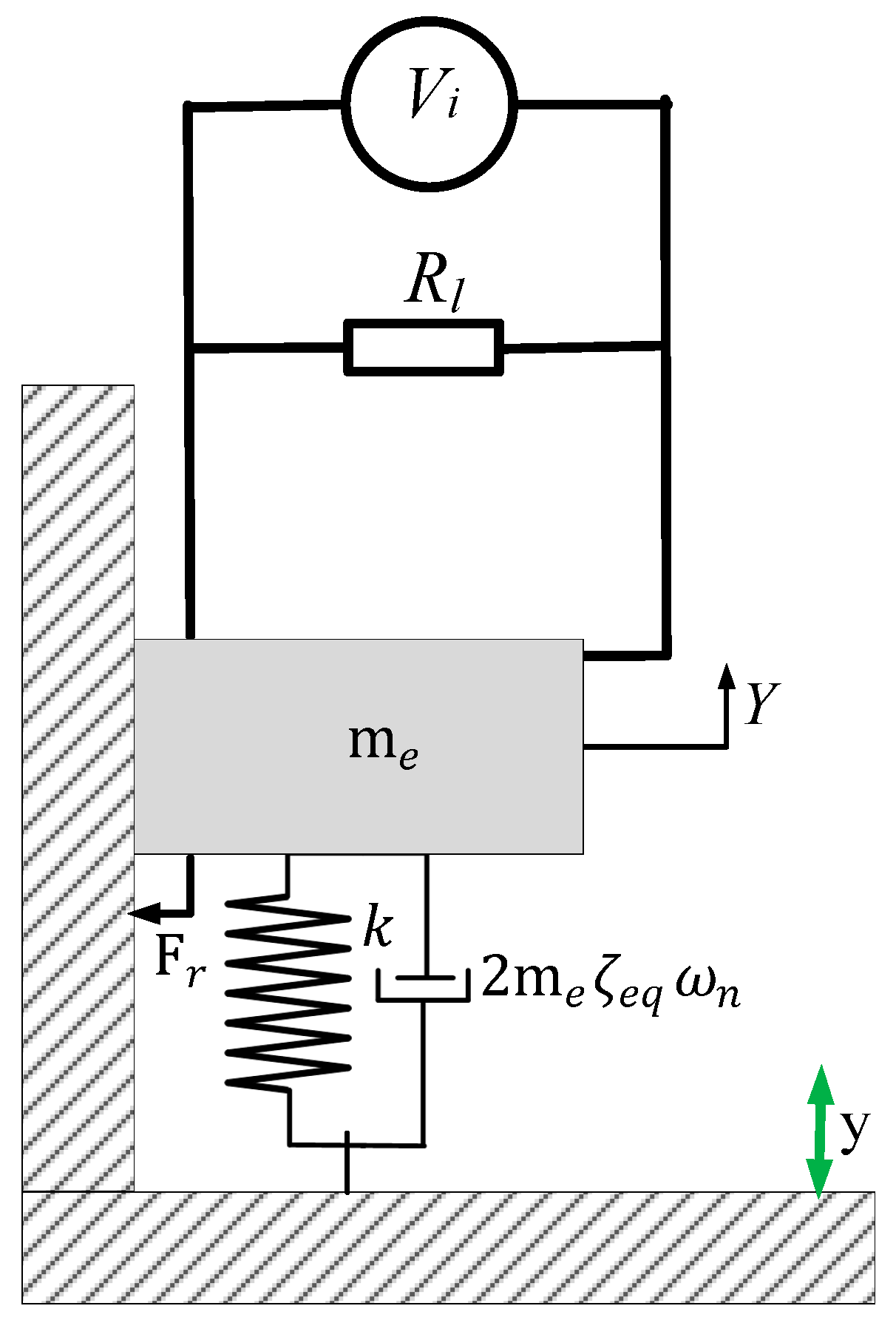
2. Governing Equation of a Spring-Mass Model
3. Transducer Coil–Magnet Models
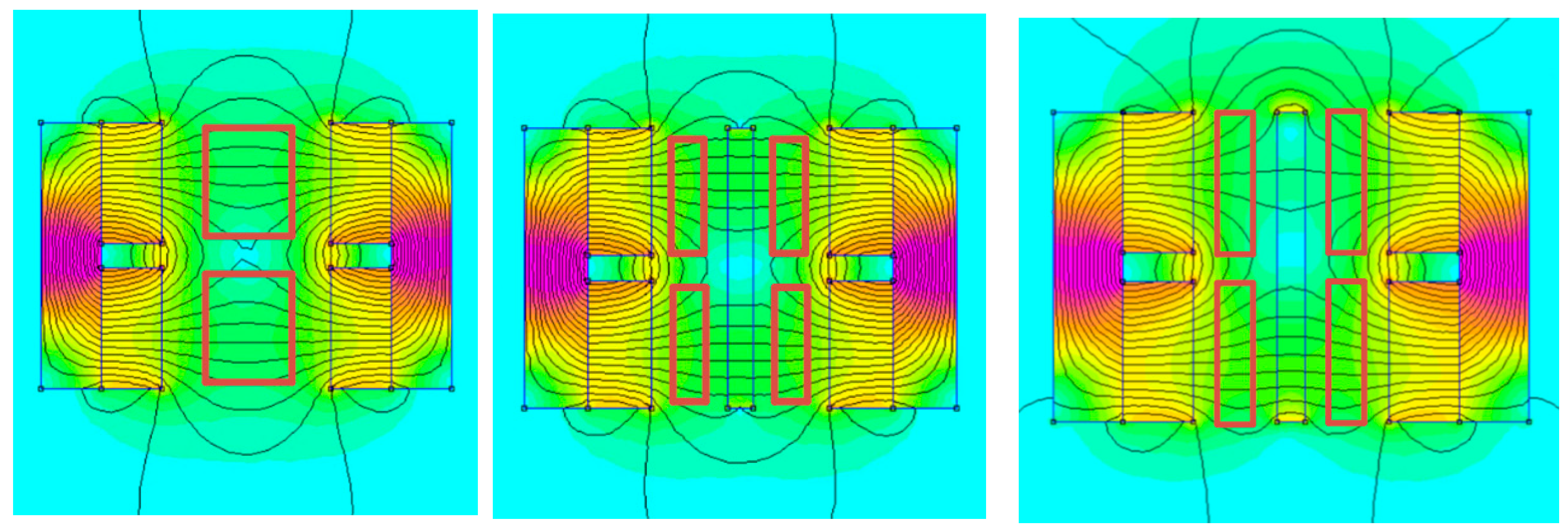
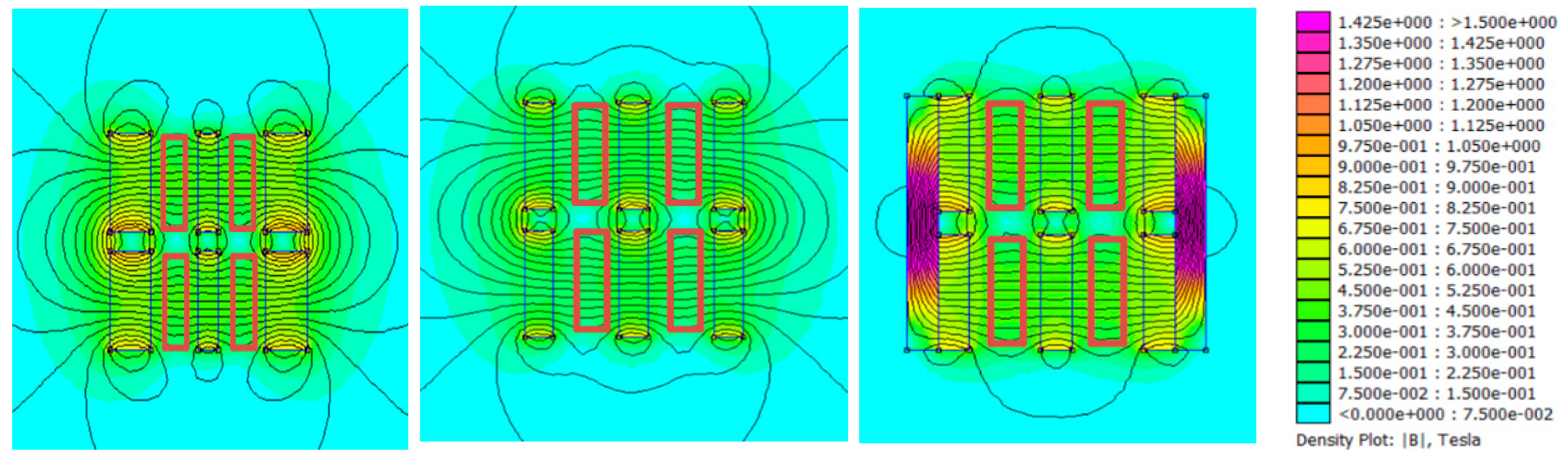
4. Finite Element Magnetic Method (FEMM) Simulation
5. Results and Parametric Analysis
- and variation: This stage of analysis briefly illustrates the variations in and as a function of the transducer geometrical volume. The flux density per unit volume of the transducer is independently compared as a ratio of total volume and magnet volumes, as shown in Table 2. Table 2 shows that although configuration a1 has the largest , for configuration c3 is improved by approximately 21.66%, 31.64%, 38.92%, 43.72% and 31.40%, respectively, relative to configurations a1, b1, b2, c1 and c2. Also, the for configuration c3 is improved by 15.77%, 13.39%, 28.17%, 5.93% and 13.38%, respectively, relative to configurations a1, b1, b2, c1 and c2. Therefore, configuration c3 was identified to attain this preferential density value at the smallest magnet and a total volume of 0.3750 and 1.3200 compared to others. This suggests that c3 is good enough to represent the improvement in the by approximately 30.00% over other configurations. As shown in the next section, this improvement will definitely result in the efficient utilization of the available magnet flux/magnet volume to induce and enhance the operational efficiency of the system.
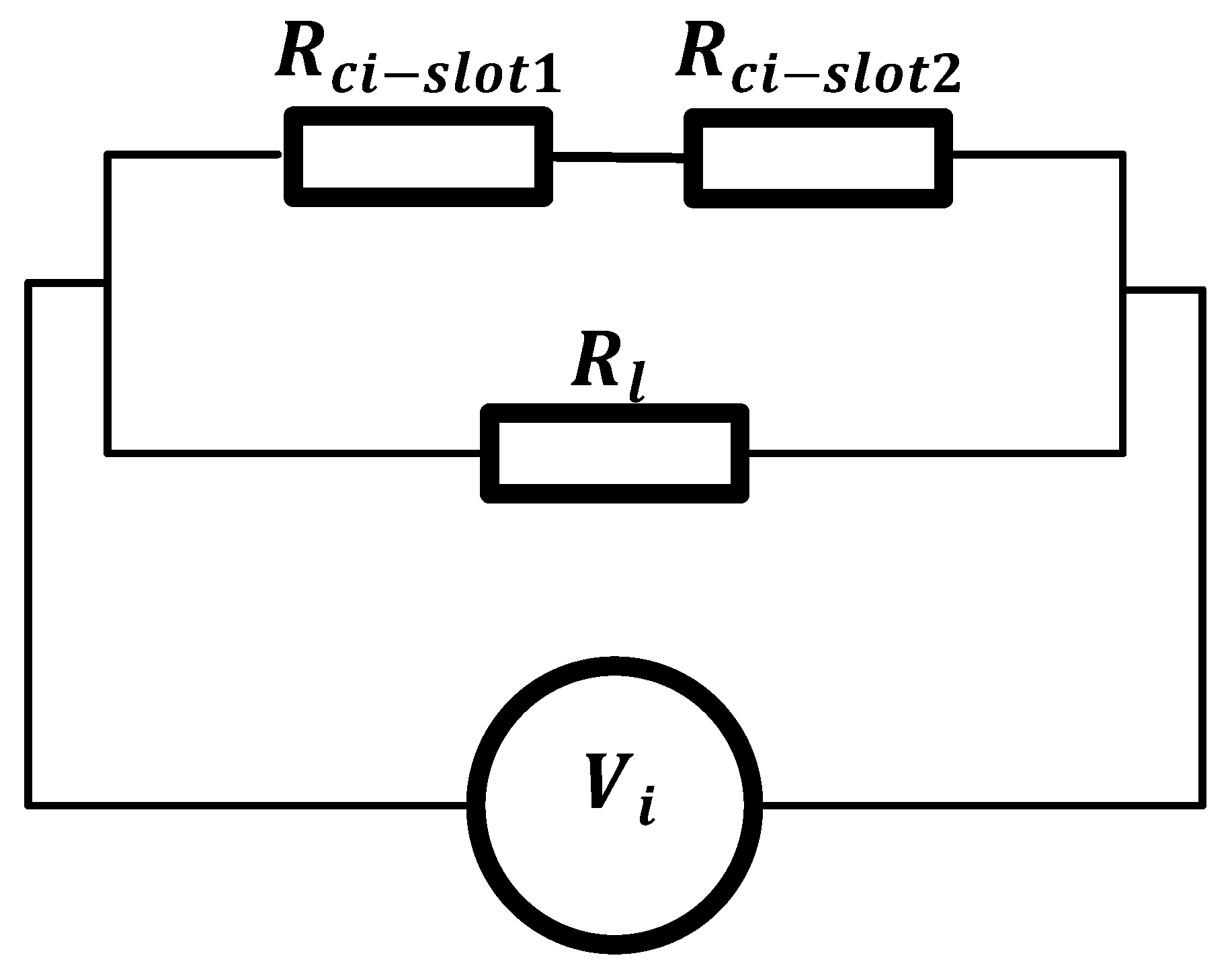
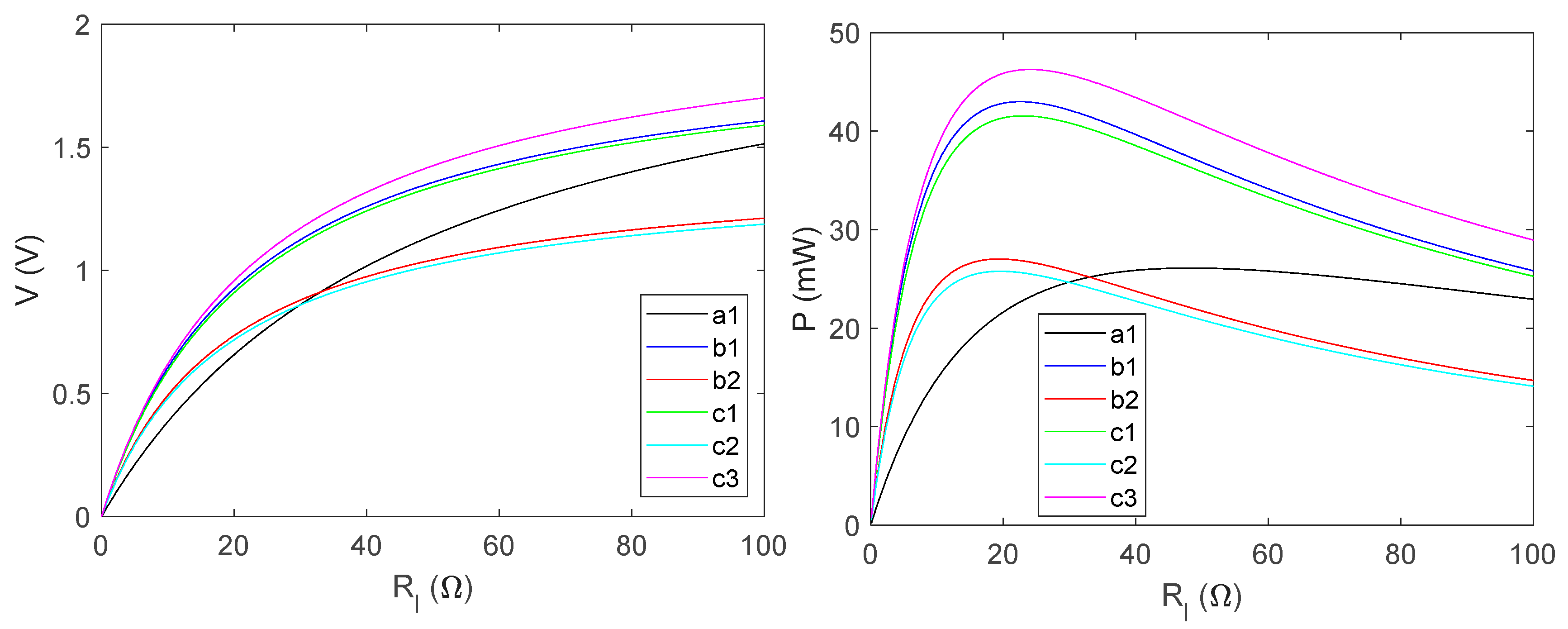
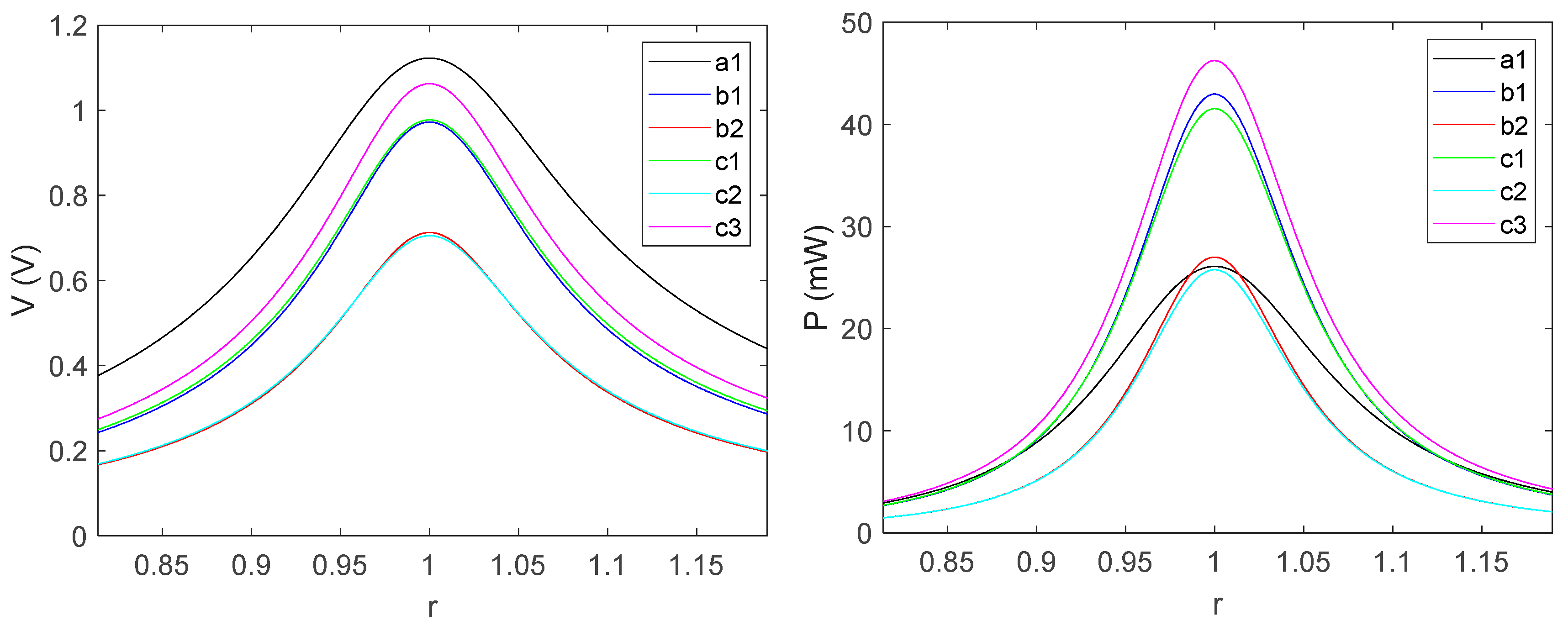
- and variation: This stage of analysis briefly illustrated the variations in the harvested voltages and power as a function of different electrical parameters. Using configuration 1, which has an 8 mm coil width as the reference, configurations 2, 3, 4, 5 and 6, however, use two split 4 mm in the double slot sections of the transducer. To characterize this variation, the coil in each slot point is connected to external load resistances, as shown in Figure 5.
6. Conclusions
- A transducer model configuration with the smallest volume attained the highest possible flux density per transducer magnet volume.
- Although flux guiding steel, which minimizes flux leakages, is often required to enhance flux coupling, configuration c2, which has no such guiding steel, shows a satisfactory performance next to c3 in terms of flux density per unit magnet/total volume, optimum load, harvested voltages and power. The implication of this is that smaller-volume, lightweight but efficient energy conversion/flux coupling is attainable in c3.
- The analysis showed that using split-slotted coils is more efficient for energy harvesting than using bulk single-equivalent coils. This is because the split coil will encourage more flux coupling/field interaction with the coil than bulk coil.
- The implication of the above implies that while larger power is available for harvesting over a series connected split coil than for the bulk coil, the optimal load capacity is considerably reduced by approximately 50.00%. Therefore, for efficient energy conversion and maximized power applicability, the series connected split coils boast usability for low-impedance systems, while bulk coil is suitable for high-impedance matching.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Priya, S.; Inman, D.J. Energy Harvesting Technologies; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175–R195. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy Harvesting From Human and Machine Motion for Wireless Electronic Devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Elvin, N.G.; Erturk, A.A. Advances in Energy Harvesting Methods; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Toluwaloju, T.I.; Thein, C.K.; Halim, D. A parametric analysis on performance dependence of electromagnetic vibration harvester on the coil position, coil connection, and magnetic flux density. In Proceedings of the 2022 International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Maldives, 16–18 November 2022; pp. 1–6. [Google Scholar]
- Saha, C.R.; O’Donnell, T.; Wang, N.; McCloskey, P. Electromagnetic generator for harvesting energy from human motion. Sens. Actuators A Phys. 2008, 147, 248–253. [Google Scholar]
- Zhu, D.; Roberts, S.; Tudor, M.J.; Beeby, S.P. Design and experimental characterization of a tunable vibration-based electromagnetic micro-generator. Sens. Actuators A Phys. 2010, 158, 284–293. [Google Scholar] [CrossRef]
- Shu, Y.; Lien, I.; Wu, W. An improved analysis of the performance of a piezoelectric energy harvester. Smart Mater. Struct. 2007, 16, 2253–2264. [Google Scholar] [CrossRef]
- Toluwaloju, T.I.; Yadav, D.; Thein, C.K.; Halim, D. Investigation on the effect of magnetic coupling and power harvested in an electromagnetic vibration energy harvester. In Proceedings of the 2022 IEEE International Conference on Industrial Technology (ICIT), Shanghai, China, 22–25 August 2022; pp. 1–6. [Google Scholar]
- Zhu, D.; Beeby, S.P.; Tudor, M.J.; Harris, N.R. Electromagnetic Vibration Energy Harvesting using an Improved Halbach Array. Smart Mater. Struct. 2012, 20, 022001. [Google Scholar]
- Priya, S. Advances in energy harvesting using low profile piezoelectric transducers. J. Electroceram. 2007, 19, 165–182. [Google Scholar] [CrossRef]
- Adhikari, S.; Friswell, M.I.; Inman, D.J. Piezoelectric energy harvesting from broadband random vibrations. Smart Mater. Struct. 2009, 18, 115005. [Google Scholar] [CrossRef]
- Foong, F.M.; Thein, C.K.; Yurchenko, D. A two-stage electromagnetic coupling and structural optimization for vibration energy harvesters. Smart Mater. Struct. 2020, 29, 085002. [Google Scholar]
- Tao, K.; Tang, L.; Wu, J.; Lye, S.W.; Chang, H.; Miao, J. Investigation of multimodal electret-based MEMS energy harvester with impact-induced nonlinearity. J. Microelectromech. Syst. 2018, 27, 276–288. [Google Scholar]
- Deng, Q.; Liu, Y.; Ci, L. A multi-magnet vibration energy harvester using ferromagnetic yokes to increase the power density. Appl. Energy 2017, 208, 1246–1253. [Google Scholar]
- Xie, L.; Cai, Y.; Dai, Q. A segmented magnet design for improved performance of linear electromagnetic vibration energy harvester. Mech. Syst. Signal Process. 2019, 127, 523–537. [Google Scholar]
- Zhou, S.; Cao, J.; Erturk, A.; Lin, J. Enhanced broadband piezoelectric energy harvesting using rotatable magnets. Appl. Phys. Lett. 2013, 102, 173901. [Google Scholar] [CrossRef]
- Toluwaloju, T.I.; Thein, C.K.; Halim, D. Flux feedback mechanism for realizing enhanced flux density in an electromagnetic vibration energy harvester. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Canary Islands, Spain, 19–21 July 2023; pp. 1–6. [Google Scholar]
- Peng, W.; Ni, Q.; Zhu, R.; Fu, X.; Zhu, X.; Zhang, C.; Liao, L. Triboelectric-electromagnetic hybrid wind energy harvesting and multifunctional sensing device for self-powered smart agricultural monitoring. Nano Energy 2024, 131, 110272. [Google Scholar] [CrossRef]

| Configuration | i | |||||||
|---|---|---|---|---|---|---|---|---|
| a | 1 | 22.00 | 2.00 | 10.00 | 8.00 | 5.00 | 5.00 | 0.00 |
| b | 1 | 22.00 | 2.00 | 10.00 | 4.00 | 5.00 | 5.00 | 2.50 |
| 2 | 22.00 | 2.00 | 10.00 | 4.00 | 5.00 | 5.00 | 2.50 | |
| c | 1 | 22.00 | 2.00 | 10.00 | 4.00 | 5.00 | 0.00 | 2.50 |
| 2 | 22.00 | 2.00 | 10.00 | 4.00 | 2.50 | 0.00 | 2.50 | |
| 3 | 22.00 | 2.00 | 10.00 | 4.00 | 2.50 | 2.50 | 2.50 |
| Config. | b (T) | |||||
|---|---|---|---|---|---|---|
| a1 | 9.750 | 0.382 | 0.5000 | 1.6362 | 7.6458 | 2.3364 |
| b1 | 14.000 | 0.332 | 0.5000 | 1.8700 | 6.6718 | 1.7890 |
| b2 | 14.000 | 0.244 | 0.6250 | 1.8700 | 5.9611 | 1.9923 |
| c1 | 14.000 | 0.343 | 0.6250 | 1.3200 | 5.4931 | 2.6092 |
| c2 | 14.000 | 0.251 | 0.3750 | 1.0450 | 6.6950 | 2.4025 |
| c3 | 14.000 | 0.368 | 0.3750 | 1.3200 | 9.7598 | 2.7737 |
| Config. | a1 | b1 | b2 | c1 | c2 | c3 |
|---|---|---|---|---|---|---|
| 48.300 | 22.000 | 18.800 | 23.000 | 19.300 | 24.400 | |
| 26.102 | 42.980 | 27.012 | 41.543 | 25.774 | 46.255 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toluwaloju, T.; Thein, C.K. Enhancing Voltage and Power Output Through the Structural Optimization of Coil–Magnet Transducers in Electromagnetic Vibration Energy Harvesters. Eng. Proc. 2024, 82, 105. https://doi.org/10.3390/ecsa-11-20405
Toluwaloju T, Thein CK. Enhancing Voltage and Power Output Through the Structural Optimization of Coil–Magnet Transducers in Electromagnetic Vibration Energy Harvesters. Engineering Proceedings. 2024; 82(1):105. https://doi.org/10.3390/ecsa-11-20405
Chicago/Turabian StyleToluwaloju, Tunde, and Chung Ket Thein. 2024. "Enhancing Voltage and Power Output Through the Structural Optimization of Coil–Magnet Transducers in Electromagnetic Vibration Energy Harvesters" Engineering Proceedings 82, no. 1: 105. https://doi.org/10.3390/ecsa-11-20405
APA StyleToluwaloju, T., & Thein, C. K. (2024). Enhancing Voltage and Power Output Through the Structural Optimization of Coil–Magnet Transducers in Electromagnetic Vibration Energy Harvesters. Engineering Proceedings, 82(1), 105. https://doi.org/10.3390/ecsa-11-20405






