Abstract
Skeletonization involves simplifying dense large-scale water distribution network (WDN) models by preserving key components that significantly impact network behavior. This study explores five WDNs and implements various skeletonization techniques to help identify a universal criterion for the optimal level of simplification. Results suggest that diverse skeletonization methods affect network topology and hydraulic accuracy. Single-method techniques tend to preserve hydraulic accuracy better but remove fewer pipes, while hybrid methods sacrifice accuracy for simplified topologies and computational time. In addition, a comparative analysis of SkelEpanet and WNTR software shows comparable performance. Ultimately, this work contributes to addressing uncertainties in transferability to real-world networks.
1. Introduction
The integration of mathematical models in water distribution network (WDN) analysis has revolutionized scenario simulation, eliminating the need for physical experimentation [1]. Skeletonization is a vital process in WDN analysis; it simplifies WDN models for easier optimization and better network management [2]. Various skeletonization methods have emerged over the past two decades to simplify models while maintaining hydraulic behavior to predetermined standards [3]. However, due to differences in WDN capacities and operational modes, furthering research is essential to develop new approaches that suit diverse network requirements [2]. The process of modeling WDNs requires a careful balance between simplicity and hydraulic accuracy [4]. In the current literature, it is unclear whether a threshold exists for skeletonizing a dense model while maintaining hydraulic and topological consistency with the original. A universal criterion for determining an appropriate level of model simplification is currently unclear, causing uncertainty regarding the trade-off between computational efficiency and hydraulic accuracy. This study aimed to address this gap by examining five WDNs with varying parameters and employing skeletonization techniques such as pipe size thresholds, branch trimming, and series and parallel pipes merging. By determining the optimal level of skeletonization and balancing computational efficiency with hydraulic accuracy and topology, this research contributes to advancing WDN modeling practices and addressing uncertainties in model transferability to real-world networks.
2. Materials and Methods
The study examined five WDNs (four real-world and one hypothetical). The study employed Python libraries for network attribute extraction, precise data preprocessing, and pipe size threshold determination. Skeletonization was performed using WNTR version 1.2.0 [5] and SkelEpanet version 2 [6], followed by EPANET simulation, to model the hydraulic behavior of the networks. Post-simulation analysis compared pressure values to evaluate model accuracy. Conclusions and recommendations were drawn based on the average relative error in pressure (AREP) analysis [7] as percentage and skeletonization results, striving to ascertain the optimal level of skeletonization balancing computational efficiency, hydraulic accuracy, and network topology.
2.1. Initial WDNs Attributes
The examined networks vary in number of pipes, ranging from 1000 to 13,000 (Table 1), aiming to encompass a wide range of real-world network sizes and complexities.

Table 1.
Initial attributes of the five networks used in this work.
2.2. Determination of Pipe Size Thresholds
The pipe size thresholds across the five networks are detailed in Table 2. In the FiveRes network, a 620 mm threshold was set for 600 mm pipes. BIWS opted for a range under 180 mm. Network-H prioritized larger pipes despite most being under 8 in (305 mm). BPDRR set a 300 mm threshold, accommodating prevalent and larger sizes. E-Town opted for higher thresholds due to the higher number of pipes in the network. Based on a preliminary analysis, thresholds were selected that enhanced skeletonization according to network-specific characteristics.

Table 2.
The selected pipe size thresholds for skeletonizing the networks.
3. Results and Discussions
This paper used the FiveRes network as a case study to demonstrate the impact of different skeletonization methods on the network’s topology. Results from E-Town were referenced to explain the effects of skeletonization on network attributes and hydraulic characteristics. The skeletonization techniques were abbreviated as parallel pipes merging (SP), branch pipes trimming (SB), series pipes merging (SS), combination of branch pipes trimming and parallel pipes merging (SBP), combination of branch pipes trimming and series pipes merging (SBS), and combination of series and parallel pipes merging (SSP).
3.1. Effect of Skeletonization Techniques on the Network Characteristics
Table 3 presents results from skeletonization techniques applied to the E-Town network with varying pipe size thresholds. The percentage of pipes removed (PPR) provides insight into how skeletonization affects the attributes of the WDN, while the AREP offers a measure of the impact on the hydraulic properties. Generally, SP and SB remove fewer pipes (0.03% to 12.06%) with low average relative error in pressure (0.0001 to 0.006), whereas SS and its combinations with other techniques (SSP and SBS) remove a higher percentage of pipes (7.32% to 40.39%) and result in higher average relative errors in pressure (1.073 to 9.368), which is disadvantageous [7]. The combination of SBP shows intermediate results in both pipe removal percentage (4.95% to 12.32%) and average relative error in pressure (0.003 to 0.007). The resulting topologies of the network at a single size threshold, as observed in Figure 1, are consistent with the number of pipes removed.

Table 3.
Results obtained after skeletonizing the E-Town network.
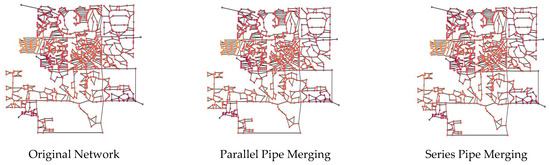
Figure 1.
Resulting topologies of the FiveRes after skeletonization using different techniques.
3.2. Comparison of SkelEpanet and WNTR
SkelEpanet and WNTR show comparable performance in skeletonizing networks, with slight inconsistencies in the percentage of links and nodes removed. SkelEpanet lacks adjustable pipe size thresholds but aligns with WNTR at the smallest thresholds. In the FiveRes network, both yield identical results, as shown in Table 4, indicating their effectiveness in skeletonizing WDNs.

Table 4.
Comparison of SkelEpanet results and WNTR using results of the FiveRes network.
4. Conclusions
Single-method techniques such as SP and SB exhibit lower rates of pipe removal compared with hybrid techniques such as SBP, SSP, and SBS. As the size thresholds increase, all techniques tend to remove a higher percentage of pipes. Consequently, as more pipes are merged, the network’s topology becomes simplified, but this simplification leads to less accurate pressure estimations. It has also been observed that there are diminishing returns at higher thresholds, suggesting that the simplification gains become less significant as the pipe size increases. These findings indicate a trade-off between model simplification and hydraulic accuracy. Therefore, the selection of the optimum level of skeletonization should consider this trade-off and prioritize the desired balance between network simplification and hydraulic accuracy for the specific real-world WDN.
This research established that both SkelEpanet and WNTR software perform comparably in WDN skeletonization, but WNTR offers flexibility in varying pipe size thresholds, giving it an edge. There are also several other packages available that can be used to simplify WDNs. This research, therefore, recommends that when choosing the optimum level of skeletonization, users need to consider factors such as computational efficiency, ease of use, and the specific requirements of their network model(s).
Author Contributions
All the authors have equally contributed to this article. All authors have read and agreed to the published version of the manuscript.
Funding
MCG is funded by WEC at Vitens N.V.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
This work has been developed under the support of the University College Dublin Ad Astra Start Up grant to the first and third authors.
Conflicts of Interest
The authors declare no conflicts of interest and no any commercial conflict of interest from VITENS N.V.
References
- AWWA. Engineering modeling applications committee. Water distribution system modeling: Past & present. J. -Am. Water Work. Assoc. 2020, 112, 10–16. [Google Scholar]
- Bello, O.; Adnan, A.M.; Yskandar, H.; Kazeem, A.; Piller, O. Solving management problems in water distribution networks: A survey of approaches and mathematical models. Water 2019, 11, 562. [Google Scholar] [CrossRef]
- Abdel-Mottaleb, N. A System Architecture for Water Distribution Networks. Ph.D. Thesis, University of South Florida, Tampa, FL, USA, 2021. [Google Scholar]
- Martínez-Solano, F.J.; Iglesias-Rey, D. Exact skeletonization method in water distribution systems for hydraulic and quality models. Procedia Eng. 2017, 186, 286–293. [Google Scholar] [CrossRef]
- Vegas Niño, Ó.T. Nuevas Herramientas Para la Gestión Técnica de Redes de Distribución de Agua Basadas en el Modelo Matemático y la Topología de la Red. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2023. [Google Scholar]
- Klise, K.; Hart, D.; Bynum, M.; Hogge, J.; Haxton, T.; Murray, R.; Burkhardt, J. Water Network Tool for Resilience (WNTR), User manual, version 0.2; 3. No. SAND-2020-9301R; EPA/600/R-20/185; Sandia National Lab (SNL-NM): Albuquerque, NM, USA, 2020. [Google Scholar]
- Truong, H.; Tello, A.; Lazovik, A.; Degeler, V. Graph neural networks for pressure estimation in water distribution systems. Water Resour. Res. 2023, 148, 04022018. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).