Accelerating Urban Drainage Simulations: A Data-Efficient GNN Metamodel for SWMM Flowrates ^†

Abstract

Computational models for water resources often experience slow execution times, limiting their application. Metamodels, especially those based on machine learning, offer a promising alternative. Our research extends a prior Graph Neural Network (GNN) metamodel for the Storm Water Management Model (SWMM), which efficiently learns with less data and generalizes to new UDS sections via transfer learning. We extend the metamodel’s functioning by adding flowrate prediction, crucial for assessing water quality and flooding risks. Using an Encoder–Processor–Decoder architecture, the metamodel displays high accuracy on the simulated time series. Future work is aimed at incorporating more physical principles and testing further transferability.

1. Introduction

Water network modelers use numerical solvers, e.g., the Storm Water Management Model (SWMM), for estimating water depths at the nodes and flow rates through the pipes as responses to rainfall. Nevertheless, multiple applications in urban water networks (e.g., optimization, real-time control, uncertainty analysis) require a large number of simulations and, depending on the speed of execution of the model, these applications may be impractical or impossible [1].

Recently, machine learning (ML) models, particularly multilayer perceptrons (MLPs), have gained popularity as alternative simulators in urban water networks [1] by learning to replicate the response of the physically based model. However, their reliance on computationally expensive training datasets and inherent case-specificity limit their broader applicability.

Previously, in [2], we developed a model based on a Graph Neural Network (GNN) architecture for emulating the response of SWMM in estimating the water depths at the nodes of a storm water system. We showed that the model was 98.1% accurate overall, being 92% accurate for periods when there is water in the nodes and 99.7% accurate when there is not. Furthermore, the model required less data and training time for efficient learning. The model’s relational inductive bias facilitated generalizing the learned weights to an unseen section of the same storm water system, enabling transfer learning for further efficiency gains.

While the previous model shows high performance for predicting water depths, it does not replicate the flow rates. This is a key edge variable for multiple applications in civil engineering, including water quality analyses and flooding estimations.

This research enhances the current model’s capabilities by including flow rate prediction by proposing the first GNN-based metamodel for flow rates in UDSs.

2. Materials and Methods

The proposed model operates on real-time information to predict the system state at the next time step. Its Encoder–Processor–Decoder structure, inspired by successful techniques for solving PDEs [3] like SWMM’s underlying equations, allows for an auto-recursive prediction of water depths and flows.

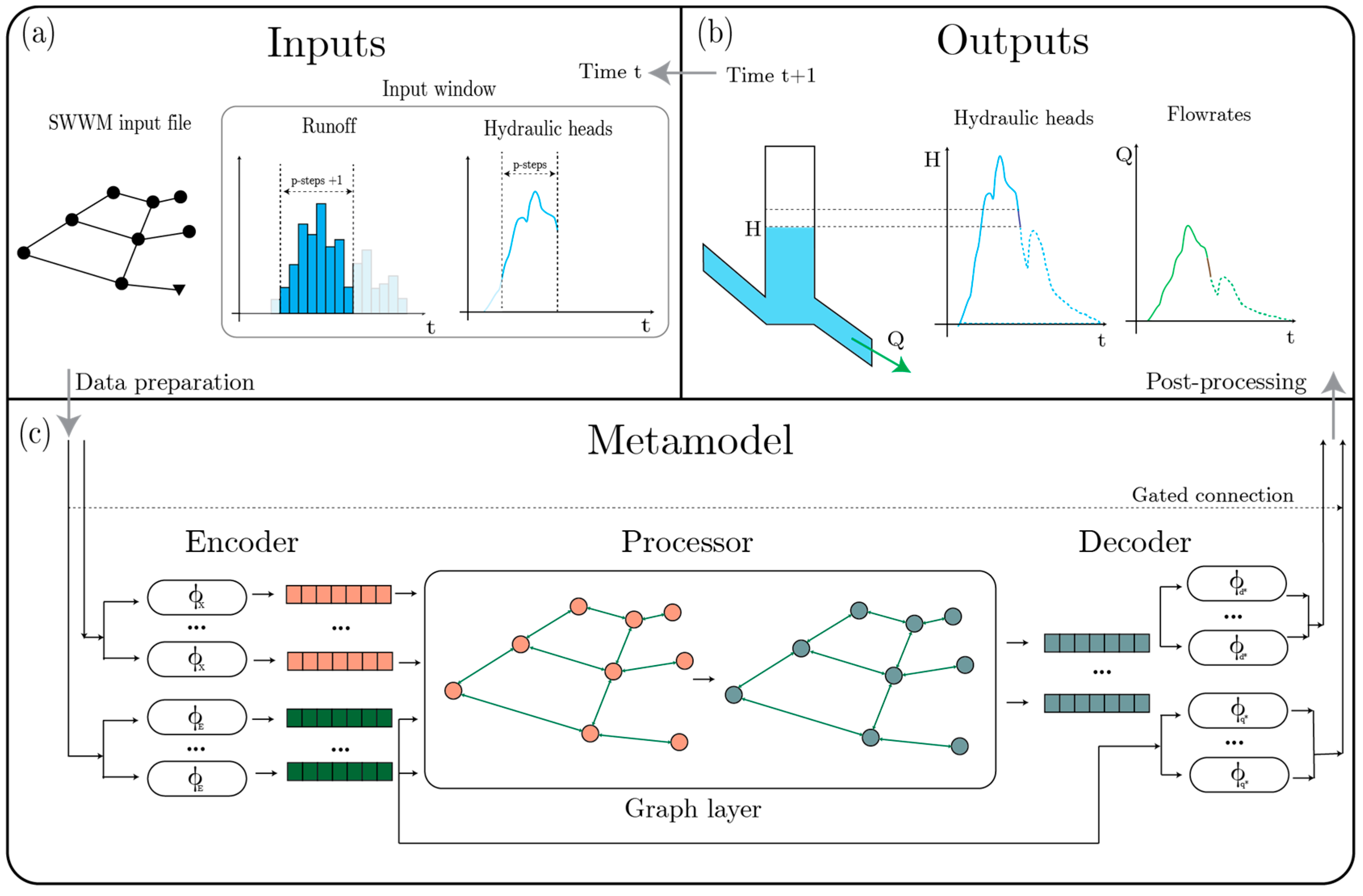
The model receives the information in current time (see Figure 1a) and its response is the state of the system at the next time step (see Figure 1b). The proposed model follows an Encoder–Processor–Decoder structure (see Figure 1c). As its name suggests, this architecture has three stages. In the first stage, the physical data both in the nodes (i.e., runoff, hydraulic head) and in the pipes (i.e., diameter, length) are embedded in higher dimensional spaces by means of multilayer perceptrons (MLPs). This representation is processed by a graph layer named GINEConv [4], which uses the connectivity of the drainage system layout.

Figure 1. Summary of the process to generate a prediction for one future time step of depths and flow rates. Subsequent predictions are obtained by iteratively repeating this process. (a) shows the inputs: partial time series of runoff and water depths, and system information (topology, node elevation, pipe diameters, and lengths). These data are organized in windows and normalized before entering the artificial neural network. (b) shows the metamodel structure in three stages: Encoder, Processor, and Decoder. The Encoder is a set of two multilayer perceptrons, $\mathrm{\varphi }$, that separately computes the embedding of nodes (pictured in pink) and pipes (pictured in green). These embeddings are fed to the graph layer which computes new node embeddings (pictured in gray). The output of this phase is then decoded by the Decoder, a set of two MLPs that transform the processed embeddings into raw predictions of the physical variables, i.e., depth (${\mathrm{d}}^{\ast }$) and flow rate (${\mathrm{q}}^{\ast }$). These quantities are marked with an asterisk to indicate they have not been post-processed. (c) shows the new predictions of depths and flow rates after being post-processed. Having these values, the process repeats to determine the entire time series. This diagram is adapted from [2] to illustrate the modification of the method.

In the third stage, the processed embeddings are used for calculating the predicted water depths and flow rates. The embeddings at the nodes feed two separate trains of calculation. For the depths, the embeddings are decoded using a shared MLP that estimates the change in depth. For the flow rates, the embeddings in the two endpoints of each edge are summed. By integrating these embeddings through a commutative operation, the predefined orientation of the edges becomes irrelevant. These values are then concatenated with the previously encoded edge features. A shared MLP for the edges takes this information for each pipe and produces a prediction for the change in flow rates.

Each prediction is weighted and summed with the respective previous depth or flow rate to obtain the final predictions in any given time step. Finally, the results are constrained to meet the physical restrictions of possible minimum and maximum depth levels, as shown in [5]. This response can be used as a starting point for the next time step; consequently, it is possible to iteratively predict the entire time series for all nodes and edges in the network.

We demonstrate the capabilities of our approach for a storm water system based on part of the city of Utrecht, The Netherlands.

Training Strategy

We used the pre-trained model weights of the best model found in [2]. This allows the model to directly predict the water depths while maintaining its high performance. These transferred parameters were frozen and the edge decoder was trained by minimizing the Mean Square Error (MSE) on the flow rates. All the models were programmed and trained with PyTorch.

In total, we used 130 rainfall events to run the simulations. To avoid data leakage, we used the same split for training and validation subsets that was used in [2]. The training subset consisted of 100 events (80 real, 20 synthetic). The validation subset consisted of 30 events (15 real, 15 synthetic).

3. Results

Table 1 summarizes the accuracy of the model when reconstructing the time series of flow rates in the validation dataset. Overall, the model achieves an error of about $1.82 \times {10}^{-4}$ ${\mathrm{m}}^3/\mathrm{s}$. In the most relevant part of the time series emulation, the period when there is water flowing in the pipes, the error is around $10.5\times {10}^{-4}$ ${\mathrm{m}}^3/\mathrm{s}$. Both values are very low in comparison to the possible range of values that the flow rates can be, i.e., over $2 {\mathrm{m}}^3/\mathrm{s}$ for this drainage system.

Table 1. Descriptive statistics of accuracy metrics for replicating SWMM hydraulic flow rates using the proposed model in the validation dataset.

$\mathbf{RMSE} (10^{-4}{\mathbf{m}}^3/\mathbf{s}$)	Overall	Flow	No Flow
Mean $\pm$ SD	1.82 $\pm$ 1.10	10.5 $\pm$7.18	0.17 $\pm$ 0.15
Max	4.42	28.6	0.580
Min	0	0.23	0

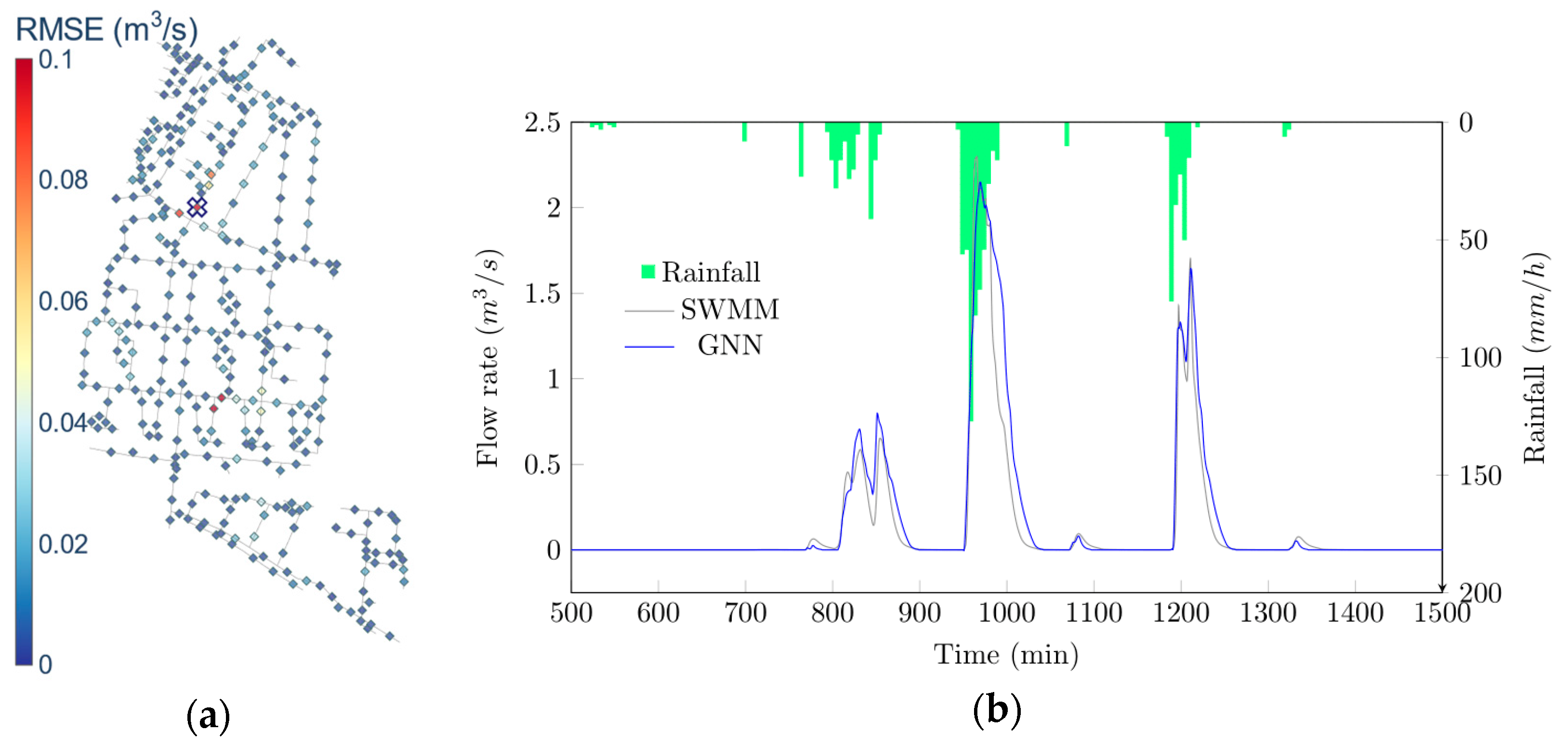
Figure 2 shows the performance of the model for an example rainfall event from the validation set. On the left side of the figure, the colored map indicates the RMSE per node. This map shows that most of the nodes have a low error. There are only a few of them with an RMSE higher than $0.05 {\mathrm{m}}^3/\mathrm{s}$. These results exemplify the high accuracy of the proposed extension of the model.

Figure 2. Performance of the model for emulating flow rates during a validation rainfall event. (a) shows the distribution of Root Mean Square Error (RMSE) in the map of the storm water system. Each point represents a pipe in the map. (b) shows the original and emulated time series of flow rates for a pipe with the one of the highest RMSEs ($0.1 {\mathrm{m}}^3/\mathrm{s}$), indicated in (a) with a cross.

Figure 2b shows an example of a flow rate time series emulation of the model along with the original time series from SWMM. These time series come from a node with an RMSE of $0.1 {\mathrm{m}}^3/\mathrm{s}$; this is one of the highest errors. The agreement of the two time series, in both magnitude and time to the flow peaks, shows the high performance of the model.

In terms of speed, the proposed model is 7.35 times faster on average than the physically based model.

4. Conclusions

This research explored the use of inductive bias and transfer learning for extending the capabilities of a machine learning-based emulator of the Storm Water Management Model (SWMM). The experiments in this study focused on estimating the accuracy and speeding-up of the adapted model for predicting flows while maintaining its high performance for predicting nodal water depths. The results indicate that the model is highly accurate overall and presents an increase in speed by around 7x with respect to the original model.