Metaheuristic Algorithms for Optimization: A Brief Review †
Abstract
1. Introduction
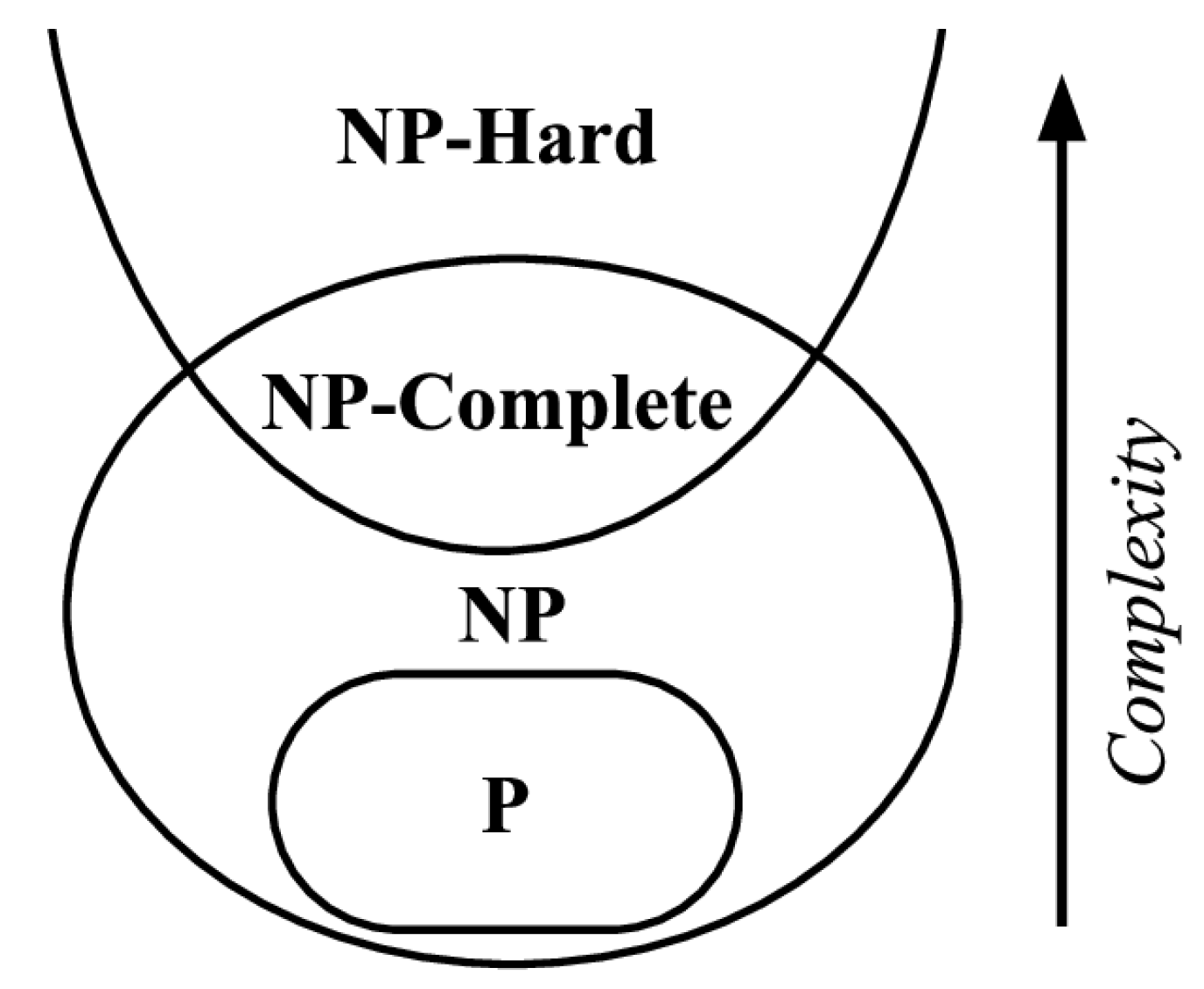
2. Optimization Problems and Metaheuristics
Optimization
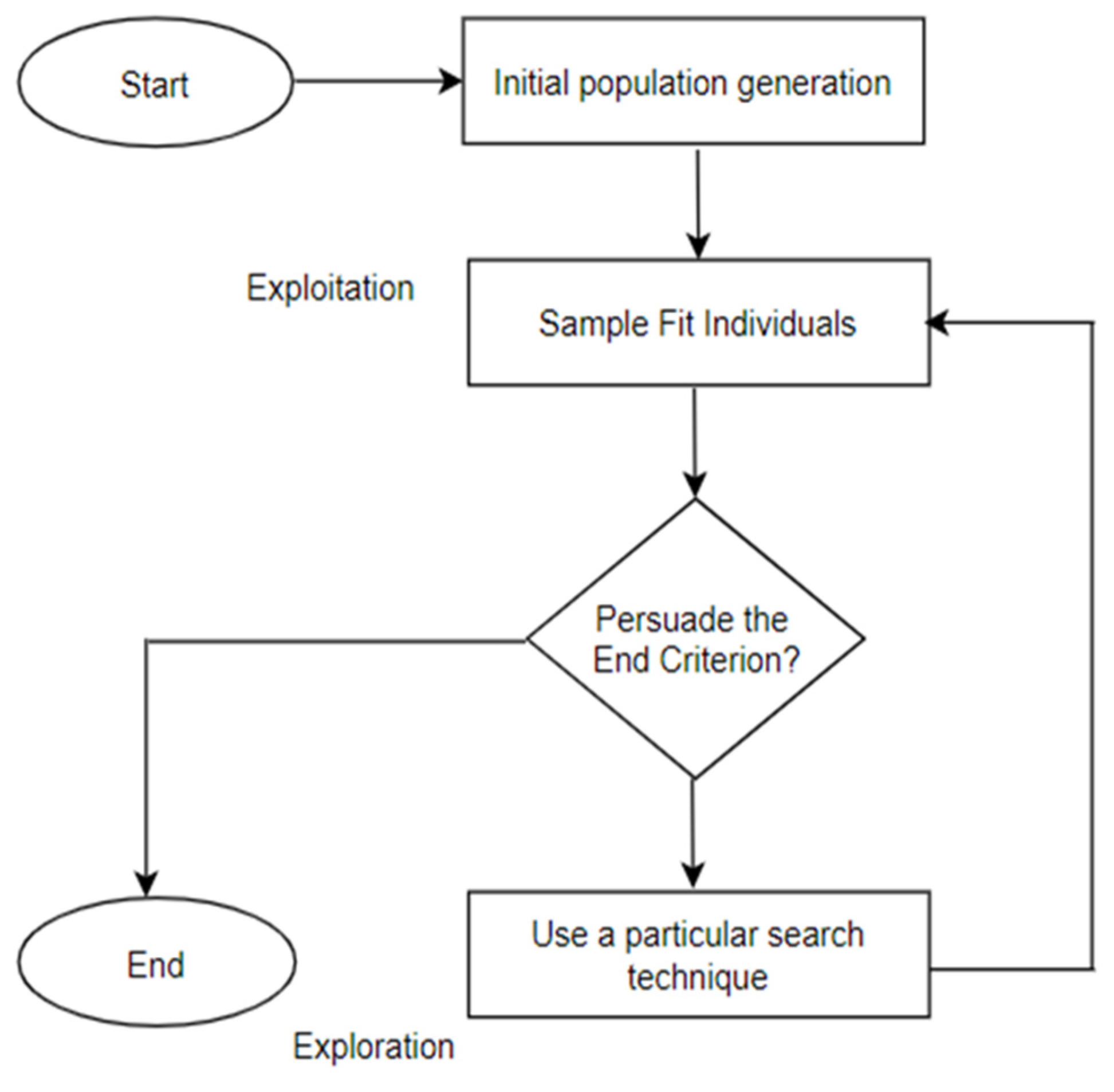
3. Framing the Metaheuristic
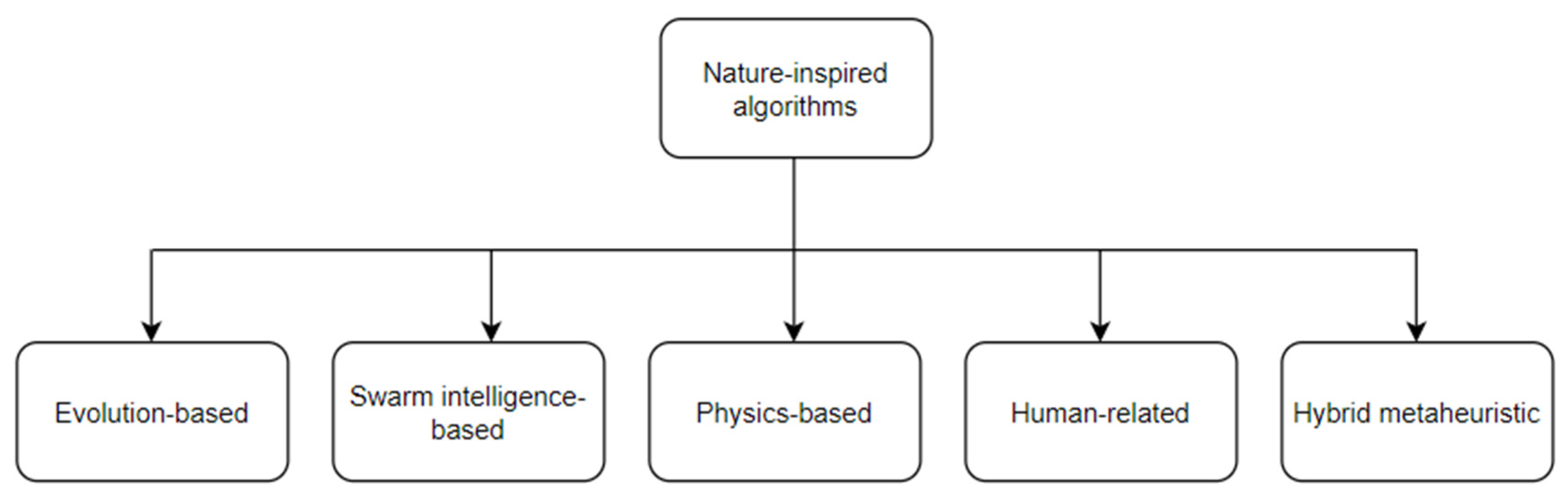
4. Categories of Metaheuristics
4.1. Evolution-Based Algorithms
4.2. Swarm Intelligence-Based Algorithms
4.3. Physics-Based Algorithms
4.4. Human-Related Algorithms
4.5. Hybrid Metaheuristic Algorithms
5. Related Research
6. Research Gaps
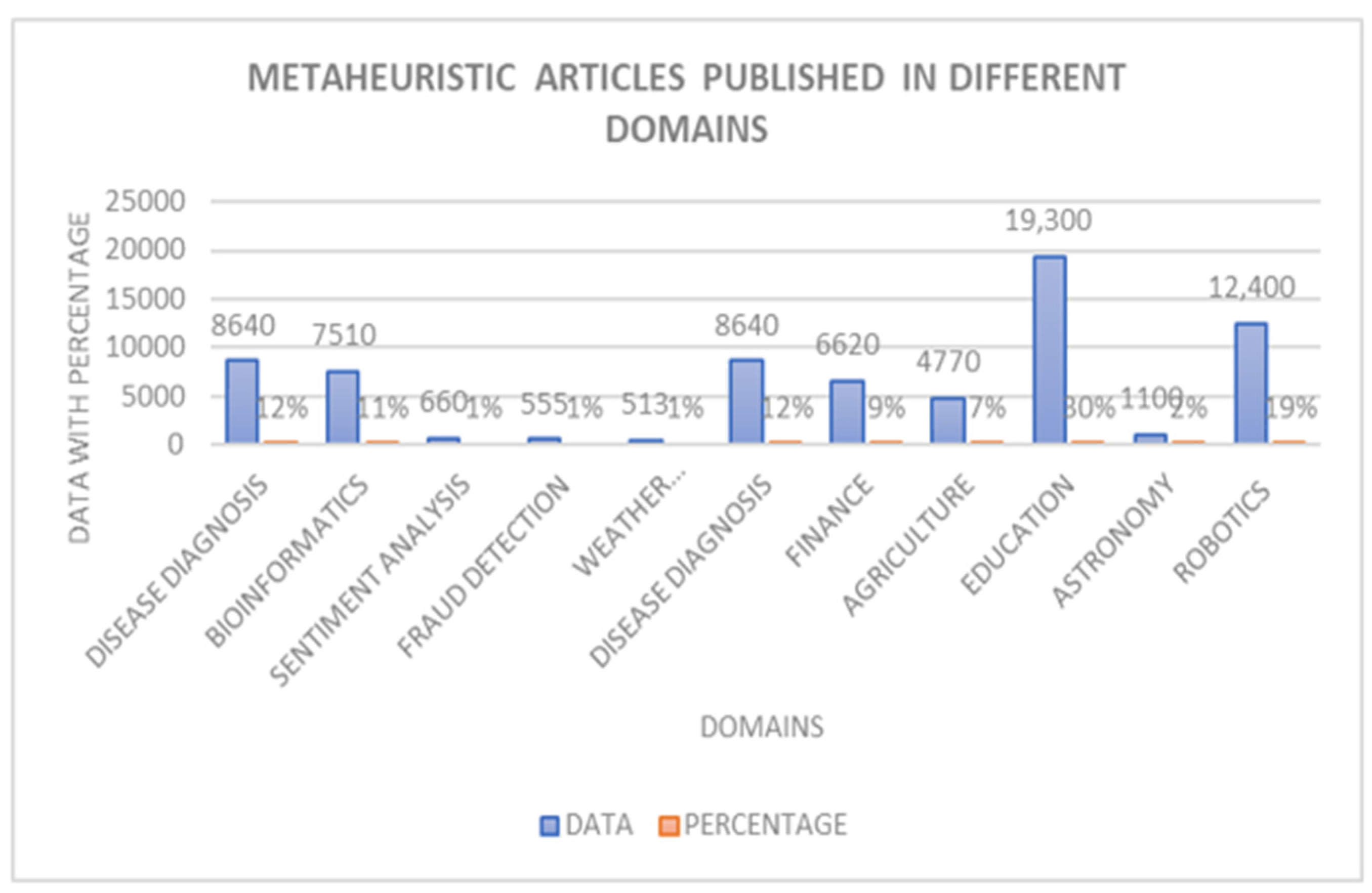
7. Practical Applications
8. Challenges in Metaheuristics
9. Conclusions and Future Scope
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Fister Jr, I.; Mlakar, U.; Brest, J.; Fister, I. A new population-based nature-inspired algorithm every month: Is the current era coming to the end? In Proceedings of the 3rd Student Computer Science Research Conference, Ljubljana, Slovenia, 12 October 2016; pp. 33–37. [Google Scholar]
- Gan, L.; Duan, H. Biological image processing via chaotic differential search and lateral inhibition. Optik 2014, 125, 2070–2075. [Google Scholar] [CrossRef]
- Negahbani, M.; Joulazadeh, S.; Marateb, H.; Mansourian, M. Coronary artery disease diagnosis using supervised fuzzy c-means with differential search algorithm-based generalized Minkowski metrics. Peertechz J. Biomed. Eng. 2015, 1, 6–14. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, J.; Li, C.; Fu, W.; Peng, T. A compound structure of ELM based on feature selection and parameter optimization using hybrid backtracking search algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 143, 360–376. [Google Scholar] [CrossRef]
- Dhal, K.G.; Gálvez, J.; Ray, S.; Das, A.; Das, S. Acute lymphoblastic leukemia image segmentation driven by stochastic fractal search. Multimedia Tools Appl. 2020, 79, 12227–12255. [Google Scholar] [CrossRef]
- Nakamura, R.Y.; Pereira, L.A.; Costa, K.A.; Rodrigues, D.; Papa, J.P.; Yang, X.S. BBA: A binary bat algorithm for feature selection. In Proceedings of the 2012 25th SIBGRAPI Conference on Graphics, Patterns and Images, Ouro Preto, Brazil, 22–25 August 2012; pp. 291–297. [Google Scholar] [CrossRef]
- Sayed, G.I.; Darwish, A.; Hassanien, A.E. A new chaotic whale optimization algorithm for features selection. J. Classif. 2018, 35, 300–344. [Google Scholar] [CrossRef]
- Rodrigues, D.; Pereira, L.A.; Almeida, T.N.S.; Papa, J.P.; Souza, A.N.; Ramos, C.C.; Yang, X.S. BCS: A binary cuckoo search algorithm for feature selection. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; pp. 465–468. [Google Scholar] [CrossRef]
- Pandey, A.C.; Rajpoot, D.S.; Saraswat, M. Feature selection method based on hybrid data transformation and binary binomial cuckoo search. J. Ambient. Intell. Humaniz. Comput. 2020, 11, 719–738. [Google Scholar] [CrossRef]
- Huang, J.; Li, C.; Cui, Z.; Zhang, L.; Dai, W. An improved grasshopper optimization algorithm for optimizing hybrid active power filters’ parameters. IEEE Access 2020, 8, 137004–137018. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary ant lion approaches for feature selection. Neurocomputing 2016, 213, 54–65. [Google Scholar] [CrossRef]
- Kanimozhi, T.; Latha, K. An integrated approach to region based image retrieval using firefly algorithm and support vector machine. Neurocomputing 2015, 151, 1099–1111. [Google Scholar] [CrossRef]
- Subha, V.; Murugan, D. Opposition based firefly algorithm optimized feature subset selection approach for fetal risk anticipation. Mach. Learn. Appl. Int. J. 2016, 3, 55–64. [Google Scholar] [CrossRef]
- Medjahed, S.A.; Saadi, T.A.; Benyettou, A.; Ouali, M. Kernel-based learning and feature selection analysis for cancer diagnosis. Appl. Soft Comput. 2017, 51, 39–48. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Heidari, A.A.; Faris, H.; Fournier-Viger, P.; Li, X.; Mirjalili, S. Binary dragonfly optimization for feature selection using time-varying transfer functions. Knowl. Based Syst. 2018, 161, 185–204. [Google Scholar] [CrossRef]
- Sharma, P.; Sundaram, S.; Sharma, M.; Sharma, A.; Gupta, D. Diagnosis of Parkinson’s disease using modified grey wolf optimization. Cogn. Syst. Res. 2019, 54, 100–115. [Google Scholar] [CrossRef]
- Pathak, Y.; Arya, K.V.; Tiwari, S. Feature selection for image steganalysis using levy flight-based grey wolf optimization. Multimed. Tools Appl. 2019, 78, 1473–1494. [Google Scholar] [CrossRef]
- Hu, P.; Pan, J.S.; Chu, S.C. Improved binary grey wolf optimizer and its application for feature selection. Knowl. -Based Syst. 2020, 195, 105746. [Google Scholar] [CrossRef]
- Rodrigues, D.; Yang, X.S.; De Souza, A.N.; Papa, J.P. Binary flower pollination algorithm and its application to feature selection. In Recent Advances in Swarm Intelligence and Evolutionary Computation; Springer: Cham, Switzerland, 2015; pp. 85–100. [Google Scholar] [CrossRef]
- Zawbaa, H.M.; Emary, E. Applications of flower pollination algorithm in feature selection and knapsack problems. In Nature-Inspired Algorithms and Applied Optimization; Springer: Cham, Switzerland, 2018; pp. 217–243. [Google Scholar] [CrossRef]
- Zawbaa, H.M.; Emary, E.; Parv, B. Feature selection based on antlion optimization algorithm. In Proceedings of the 2015 Third World Conference on Complex Systems (WCCS), Marrakech, Morocco, 23–25 November 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Hussien, A.G.; Hassanien, A.E.; Houssein, E.H.; Bhattacharyya, S.; Amin, M. S-shaped binary whale optimization algorithm for feature selection. In Recent Trends in Signal and Image Processing: ISSIP 2017; Springer: Singapore, 2017; pp. 79–87. [Google Scholar] [CrossRef]
- Tubishat, M.; Abushariah, M.A.; Idris, N.; Aljarah, I. Improved whale optimization algorithm for feature selection in Arabic sentiment analysis. Appl. Intell. 2019, 49, 1688–1707. [Google Scholar] [CrossRef]
- Papa, J.P.; Rosa, G.H.; de Souza, A.N.; Afonso, L.C. Feature selection through binary brain storm optimization. Comput. Electr. Eng. 2018, 72, 468–481. [Google Scholar] [CrossRef]
- Tuba, E.; Strumberger, I.; Bezdan, T.; Bacanin, N.; Tuba, M. Classification and feature selection method for medical datasets by brain storm optimization algorithm and support vector machine. Procedia Comput. Sci. 2019, 162, 307–315. [Google Scholar] [CrossRef]
- Oliva, D.; Elaziz, M.A. An improved brainstorm optimization using chaotic opposite-based learning with disruption operator for global optimization and feature selection. Soft Comput. 2020, 24, 14051–14072. [Google Scholar] [CrossRef]
- Jain, K.; Bhadauria, S.S. Enhanced content-based image retrieval using feature selection using teacher learning based optimization. Int. J. Comput. Sci. Inf. Secur. (IJCSIS) 2016, 14, 1052–1057. [Google Scholar]
- Balakrishnan, S. Feature selection using improved teaching learning based algorithm on chronic kidney disease dataset. Procedia Comput. Sci. 2020, 171, 1660–1669. [Google Scholar] [CrossRef]
- Allam, M.; Nandhini, M. Optimal feature selection using binary teaching learning-based optimization algorithm. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 329–341. [Google Scholar] [CrossRef]
- Agrawal, P.; Abutarboush, H.F.; Ganesh, T.; Mohamed, A.W. Metaheuristic algorithms on feature selection: A survey of one decade of research (2009–2019). IEEE Access 2021, 9, 26766–26791. [Google Scholar] [CrossRef]
- Hafez, A.I.; Hassanien, A.E.; Zawbaa, H.M.; Emary, E. Hybrid monkey algorithm with krill herd algorithm optimization for feature selection. In Proceedings of the 2015 11th International Computer Engineering Conference (ICENCO), Cairo, Egypt, 29–30 December 2015; pp. 273–277. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid binary ant lion optimizer with rough set and approximate entropy reducts for feature selection. Soft Comput. 2019, 23, 6249–6265. [Google Scholar] [CrossRef]
- Arora, S.; Singh, H.; Sharma, M.; Sharma, S.; Anand, P. A new hybrid algorithm based on grey wolf optimization and crow search algorithm for unconstrained function optimization and feature selection. IEEE Access 2019, 7, 26343–26361. [Google Scholar] [CrossRef]
- Abd Elaziz, M.E.; Ewees, A.A.; Oliva, D.; Duan, P.; Xiong, S. A hybrid method of sine cosine algorithm and differential evolution for feature selection. In Neural Information Processing: 24th International Conference, ICONIP 2017, Guangzhou, China, 14–18 November 2017; Proceedings, Part V 24; Springer International Publishing: Cham, Switzerland, 2017; pp. 145–155. [Google Scholar] [CrossRef]
- Tawhid, M.A.; Dsouza, K.B. Solving feature selection problem by hybrid binary genetic enhanced particle swarm optimization algorithm. Int. J. Hybrid Intell. Syst. 2019, 15, 207–219. [Google Scholar] [CrossRef]
- Shukla, A.K.; Singh, P.; Vardhan, M. A new hybrid wrapper TLBO and SA with SVM approach for gene expression data. Inf. Sci. 2019, 503, 238–254. [Google Scholar] [CrossRef]
| Algorithm Type | Classification | Fundamental Ideas | Applicability |
|---|---|---|---|
| Evolution-based | Genetic Algorithm (GA) | Genetic operators, population evolution | A wide range of optimization challenges |
| Swarm intelligence-based | Firefly Algorithm (FA) | Attraction and movement based on brightness | Problems in dynamic or evolving environments |
| Physics-based | Gravitational Search Algorithm (GSA) | Gravity, mass, acceleration, attraction | Problems in which physical analogies can be used |
| Human-related | Teaching-based Learning Optimization (TBLO) | Teaching strategies, collaboration, knowledge sharing | Domain-specific knowledge or constraint issues |
| Hybrid | Hybrid Metaheuristic Algorithms | Combination of multiple algorithms or techniques | Complex optimization issues with a wide range of characteristics |
| Author | Year | Algorithm Used | Application | Outcome |
|---|---|---|---|---|
| Nakamura et al. [7] | 2012 | Binary BAT Algorithm (BBA) | Feature Selection | Enhanced feature selection. |
| Rodrigues et al. [9] | 2013 | Binary Cuckoo Search (BCS) | Power System Theft Detection | Fastest and most appropriate for commercial datasets. |
| Negahbani et al. [4] | 2015 | Differential Search Algorithm | Diagnosing Coronary Artery Disease | Improved disease diagnosis precision. |
| Kanimozhi and Latha [13] | 2015 | Firefly Algorithm (FFA) and Support Vector Machine (SVM) | Region-Based Image Retrieval | Image recovery with optimal feature selection. |
| Rodrigues et al. [20] | 2015 | Binary Flower Pollination Algorithm (BFPA) | Feature Selection Problems | improved performance in feature selection. |
| Zawbaa et al. [22] | 2015 | Binary Artificial Life Optimization (BALO) | Various Datasets | In contrast to GA and PSO, continuous variable thresholds. |
| Hafez et al. [33] | 2015 | Hybrid Monkey Algorithm with Krill Herd Algorithm Optimization | Classification Accuracy | Improved solution finding by combining krill swarm and monkey algorithms. |
| Subha and Murugan [14] | 2016 | Firefly Algorithm (FFA) | Cardiotocography Data | Disease prognosis. |
| Emary et al. [23] | 2016 | Binary Ant Lion Approaches | Feature Selection | Enhanced performance in feature selection. |
| Jain and Bhadauria [29] | 2016 | Teacher Learning-Based Optimization (TLBO) | Enhanced Content-Based Image Retrieval | TLBO and SVM classifiers are used to optimize feature selection. |
| Zhang et al. [5] | 2017 | Hybrid Backtracking Search Algorithm | Wind Speed Forecasting | Extreme learning machines were used, and good results were obtained. |
| Medjahed et al. [15] | 2017 | Binary Dragonfly Algorithm (BDF) | Cancer Diagnosis | Increased execution and production of SVM-RFE. |
| Abd Elaziz et al. [36] | 2017 | Hybrid Sine/Cosine Algorithm with Differential Evolution (DE) | Feature Selection Problem | Local optima were eliminated, and statistical analysis and power measurements were improved. |
| Mafarja et al. [16] | 2018 | Binary Dragonfly Algorithm (BDA) | Feature Selection Problems | When compared to metaheuristic optimization, time-varying transfer functions. |
| Zawbaa and Emary [21] | 2018 | Flower Pollination Algorithm | Feature Selection, Knapsack Problems | Superior than other algorithms in performance. |
| Sayed et al. [8] | 2018 | Chaotic Whale Optimization Algorithm (CWOA) | Feature Selection | increased harmony between algorithm research and exploitation. |
| Papa et al. [26] | 2018 | Binary Brain Storm Optimization (BBSO) | Real-world datasets | Improved categorization using the fuzzy min-max neural network learning model. |
| Sharma et al. [17] | 2019 | Gray Wolf Optimization (GWO) | Diagnosis of Parkinson’s Disease | Improved diagnostic performance with a Parkinson’s disease classification variant. |
| Pathak et al. [18] | 2019 | Levy Flight-Based Gray Wolf Optimization | Image Steganalysis | Outstanding convergence performance. |
| Hussien et al. [24] | 2019 | Whale Optimization Algorithm (WOA) | Feature Selection Problem | Achieved excellent accuracy while reducing characteristics. |
| Tubishat et al. [25] | 2019 | Improved Whale Optimization Algorithm (WOA) | Sentiment Analysis | Improved sentiment analysis using the Arabic dataset |
| Tuba et al. [27] | 2019 | Brain Storm Optimization Algorithm and Support Vector Machine (SVM) | Medical Categorization | SVM classifier integration, improved SVM parameters. |
| Mafarja and Mirjalili [34] | 2019 | Hybrid Binary Ant Lion Optimizer with Rough Set and Approximate Entropy Reducts | Performance Enhancement | The hybrid algorithm improves adoption and performance. |
| Arora et al. [35] | 2019 | Hybrid Gray Wolf Optimizer with Crow Search Algorithm (GWOCSA) | Unconstrained Function Optimization, Classification Accuracy | The hybrid algorithm increased accuracy. |
| Tawhid and Dsouza [37] | 2019 | Bat-His Algorithm with Particle Swarm Optimization (PSO) | Feature Selection Problem | A hybrid algorithm with efficient search and convergence features. |
| Shukla et al. [38] | 2019 | Hybrid Wrapper TLBO and SA with SVM Approach | Gene Expression Data | Enhanced cancer diagnosis with enhanced TLBO solution quality. |
| Dhal et al. [6] | 2020 | Speculative Fractal Forage | Optimizing Leukemia Cancer Symptom Recognition | When compared to traditional approaches, the outcomes are remarkable. |
| Pandey et al. [10] | 2020 | Binary Binomial Cuckoo Search | Various Data Sets | Best-performing functions have been identified. |
| Hu et al. [19] | 2020 | Advanced GWO (ABGWO) | Various UCI Datasets | Better results than existing algorithms. |
| Oliva and Elaziz [28] | 2020 | Improved BSO Algorithm | Eight Datasets from UCI Repository | increased categorization and enhanced search quality. |
| Balakrishnan [30] | 2020 | Multi-objective TLBO Feature Selection | Binary Classification Tasks | Models such as logistic regression, SVM, and ELM performed better. |
| Allam and Nandhini [31] | 2022 | Binary TLBO (BTLBO) | Breast Cancer Dataset | Excellent precision with fewer characteristics. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomar, V.; Bansal, M.; Singh, P. Metaheuristic Algorithms for Optimization: A Brief Review. Eng. Proc. 2023, 59, 238. https://doi.org/10.3390/engproc2023059238
Tomar V, Bansal M, Singh P. Metaheuristic Algorithms for Optimization: A Brief Review. Engineering Proceedings. 2023; 59(1):238. https://doi.org/10.3390/engproc2023059238
Chicago/Turabian StyleTomar, Vinita, Mamta Bansal, and Pooja Singh. 2023. "Metaheuristic Algorithms for Optimization: A Brief Review" Engineering Proceedings 59, no. 1: 238. https://doi.org/10.3390/engproc2023059238
APA StyleTomar, V., Bansal, M., & Singh, P. (2023). Metaheuristic Algorithms for Optimization: A Brief Review. Engineering Proceedings, 59(1), 238. https://doi.org/10.3390/engproc2023059238





