Performance Analysis of the Pilot and Data Component of a CSS Signal for LEO-PNT ^†

Abstract

From the analysis of chirp spread spectrum (CSS) signals in radar and communication applications, we can distinguish the cases of estimating only data or time-delay propagation or Doppler frequency when all the other parameters are known or set to zero. The case of estimating all three parameters at the same time has not been treated in the literature of radar or communications. We consider in this paper the use of a CSS signal for a LEO-PNT signal, which perfectly fits with the case of estimating the three parameters mentioned above. Specifically, the main goal of this paper is to explain the design of a CSS signal for PNT. This will include the design of the ranging component and the data component. The performance evaluation of both components will also be analyzed and linked. It is important to note that the focus of this paper will be the data component, and we link it with the pilot component through sensitivity performance. The results given in this paper show the capabilities of CSS for PNT. Previous works have shown accuracies on the level of meters with achievable data rates shown in this paper in the order of tens of kbps.

1. Introduction

The extended use of battery-powered devices, such as smartphones, tablets, portable computers, and wearable and IoT devices, is changing the way our technology is designed. In the last decade, there has been a trend of devices with low-power consumption and low-complexity processing. To do so, we must consider simple signal structures leading to simple receiver processing architectures. In addition, there is a trend toward targeting everywhere connectivity by relying on the satellite segment. A proof of that is the extended list of low Earth orbit (LEO) satellite constellations for internet services or IoT connectivity in the NewSpace landscape [1,2]. The opportunities of LEO constellations deal with the main challenges of IoT communication and localization systems [3,4]. One clear example joining both communication and localization is a positioning, navigation, and timing (PNT) system [5], and there is a current interest in LEO-PNT. Indeed, the first PNT results from the Starlink constellation were published in [6], and it opened a new era of alternative PNT solutions based on signals of opportunity (SoO) from LEO constellations or by the development of an alternative LEO PNT system [7].

During the past decades, the use of global navigation satellite systems (GNSSs) has become the primary and sometimes only way of providing a global PNT solution for many outdoor applications [8]. Unfortunately, GNSS is a very power-hungry technology that is vulnerable to several threats [9]. Thus, it is important to provide alternative PNT solutions to back up GNSS in case of failure or denial of service [9,10]. In this sense, the use of LEO constellations has been considered in the literature to provide a global PNT solution, but more importantly, because it will bring some benefits with respect to MEO constellations [6,7]. In this paper, we focus on the signal design for a LEO-PNT system. Different options can be adopted for the LEO-PNT signal, but if we aim to reduce complexity with respect to current GNSS, we should change the current GNSS signal structure [4,11]. Otherwise, the signal acquisition would be prohibitive for low-complexity devices. Recall that the high dynamic in LEO constellations will produce a large search space for the acquisition process of a direct-sequence spread spectrum (DSSS) signal (i.e., current GNSS signal structure) [4]. One alternative with lower acquisition complexity can be based on a chirp spread spectrum (CSS) signal.

The CSS signal has extensively been used in radar [12] since a long time ago, and it is reaching the realm of low-power wide-area networks (LPWANs) by the deployment of LoRa networks [13]. From the analysis of CSS signals in radar and communication applications, we can distinguish the cases of estimating only data or time-delay propagation or Doppler frequency when all the other parameters are known or set to zero. The case of estimating all three parameters at the same time has not been treated in the literature of radar or communications. The first time a CSS signal was considered for a PNT signal was given in [4]. Indeed, the complexity of the CSS signal was analyzed in [4], and it was compared with a DSSS signal. Improvements in terms of complexity from 1 and up to 2 orders of magnitude can be obtained using CSS with respect to DSSS. Furthermore, ref. [11] provides details on the key performance indices (KPIs) for PNT of the CSS signal. We consider in this paper the use of a CSS signal for a LEO-PNT signal, which perfectly fits with the case of estimating the three parameters mentioned above.

The goal of this paper is to explain the design of a CSS signal for PNT. This will include the design of the ranging component and the data component. The performance evaluation of both components will also be analyzed and compared. Therefore, the contribution of this paper is to complete the design of a CSS-based PNT signal by analyzing both the ranging and data component. Note that the ranging component was already introduced and evaluated in [4] and [11], respectively. In this paper, we include the design and evaluation of the data component, and we relate it with the design of the ranging component. To do so, the rest of this paper is organized as follows: Section 2 explains the signal model for the CSS-based PNT signal by showing the general expression of a CSS signal, the challenges we find in PNT, and how to solve them by including a pilot and data component. Then, Section 3 goes into detail about the signal processing and design of the CSS-based PNT signal, and Section 4 provides the performance analysis of the proposed CSS signal. Finally, Section 5 concludes the paper.

2. Signal Model

In this section, we introduce the signal model for the proposed CSS-based PNT signal in this paper. For that, let $T_{\mathrm{c}}$ be the chirp period or duration and B be the signal bandwidth. Then, a general expression for a CSS signal is given by the following waveform:

$$s\left(t\right)=e^{j2\pi {\int }_0^t{\left[f_0+\mu u\right]}_B\mathrm{d}u},$$

(1)

with $f_0$ as the initial frequency, $\mu \doteq T_{\mathrm{c}}/B$ as the chirp rate, and ${\left[·\right]}_B$ as the modulus-B operator. For a PNT signal, we have to consider the presence of data information (e.g., represented by $f_0$), time delay ($\tau$), and frequency Doppler ($f_{\mathrm{D}}$). The challenges of a CSS-based PNT signal comes from the traditional de-chirp process used in radar and communications [4]. Traditionally, the frequency of the de-chirped signal has been used to estimate either time delay, frequency Doppler, or data information. In a PNT scenario, all the parameters of interest (i.e., $\{f_0,f_{\mathrm{D}},\tau \}$) are embedded on the de-chirped frequency [4]. This scenario leads us to the transmission of two separate components: the pilot and data component. The pilot component does not carry data information, and it is used to synchronize the signal. Once the signal is synchronized, the data component is used for the reception of the useful information needed for PNT. Second, in the act of synchronizing the signal, we will extract the ranging information (i.e., time delay) needed to localize the user. Finally, it is worth noting that the design of a GNSS signal must include a multi-satellite access (MSA) scheme. These concepts are introduced in the following.

2.1. Ranging Capabilities

The most important task of a PNT signal is to provide the means for ranging. The CSS signal considered in this paper is a complex signal so that it needs both I&Q components for the transmission and reception of the signal. Therefore, the transmission of a CSS signal can be used for either ranging (i.e., $\{\tau ,f_{\mathrm{D}}\}$ estimation) or data transmission. This is in contrast with traditional GNSS [14], in which the transmitted signal is usually real and then a pilot/data scheme is transmitted through the I&Q components. Then, in our case, we should consider some way to make the ranging (pilot) component coexist with the data component, e.g., waveform multiplexing [15] or time multiplexing [4,11]. Note that for the pilot component, we have absence of data, so that we would be able to obtain the time-delay and Doppler frequency estimation using a BOK-chirp signal as defined in [4,11]. Therefore, in the following, we will assume that a BOK-chirp signal is transmitted from the satellites for the purpose of ranging/synchronization. The signal processing and design of the pilot component was studied in [4,11]. Here, in Section 3.1, we give the main ideas needed to understand the design of the data component.

2.2. Data Transmission

Once the signal is synchronized, we can assume $\tau =f_{\mathrm{D}}=0$, so that data reception can be achieved through a simple de-chirp process when transmitting the general CSS waveform in (1). The details for the data component will be given in Section 3.2. Here, let us give a summary of the advantages and drawbacks of different CSS modulations from a PNT signal design’s point of view:

• BOK-CSS: A digital modulation scheme sometimes considered in practice for chirp signals is the so-called BOK for communications [16]. Note that although considering up- and down-chirp signals, the BOK chirp scheme considered here is different from the one used in the pilot component [4]. In this case, the transmitted signal is written as

  $$s_{\mathrm{CBOK}}\left(t\right)=b\left(t\right)e^{j2\pi {\int }_0^t{\left[\mu t\right]}_B\mathrm{d}u}+(1-b\left(t\right))e^{-j2\pi {\int }_0^t{\left[\mu t\right]}_B\mathrm{d}u},$$

  (2)

  with $b\left(t\right)=\{0,1\}$ as the data bit. Note that only one bit per $T_{\mathrm{c}}$ can be sent, which limits the data-rate capability.
• PSK-CSS: A phase shift keying (PSK)-CSS modulation is given by [17]:

  $$s_{\mathrm{PSK}}\left(t\right)=e^{j(2\pi {\int }_0^t{\left[\mu u\right]}_B\mathrm{d}u+\theta \left(t\right))},$$

  (3)

  where $\theta \left(t\right)$ stands for the phase corresponding to the transmitted symbol at time t. This modulation could be useful to increase the data-rate capabilities with respect to the BOK-CSS option when considering a higher-order modulation than BPSK.
• FSK-CSS: As long as the initial frequency of (1) is not used for other purposes (e.g., satellite identification), it can be used for data delivery as performed in LoRa [13]. In that way, each symbol in an M-ary constellation is assigned to a given initial frequency, $s_k$. Then, the transmitted signal is written as

  $$s_{\mathrm{FSK}}\left(t\right)=e^{j2\pi {\int }_0^t{f}_k(u;s_k)\mathrm{d}u},$$

  (4)

  for $(k-1)T_{\mathrm{c}}\le t\le k{T}_{\mathrm{c}}$, and the instantaneous frequency given by

  $$f_k(t;s_k)={\left[s_k+\mu t\right]}_B.$$

  (5)

  This option can be useful to increase the data rate with respect to BOK-CSS, and it can provide a better alternative to PSK-CSS in terms of HW impact on current GNSS receivers. Note, once synchronized, that the demodulation of frequency shift keying (FSK)-CSS can be based on a simple de-chirp process.

2.3. Multi-Satellite Access (MSA)

Multiple satellite access with CSS can be based on two main parameters given in (1): the slope, $\mu$, and the initial frequency, $f_0$. Both parameters can be used to identify the different users. Unfortunately, there are some consequences on the selection of the MSA scheme that have to be considered when dealing with PNT. On the one hand, the use of multiple slopes may be limited when the number of satellites increases due to interference between satellites. On the other hand, when considering different frequencies for different satellites, we are intrinsically discarding an FSK-CSS modulation for the data transmission. Different schemes for MSA in PNT were proposed and analyzed in [4]. The conclusion is that the so-called multi-dual-slope (MDS) scheme provides the shortest chirp period possible among the analyzed MSA schemes in [4]. As a consequence, the MDS scheme allows us to reduce the processing complexity and to target high data-rate configurations for the data component. For the above reasons, in this paper we use the MDS scheme for the pilot component of the proposed CSS-based PNT signal. The philosophy of the MDS scheme is to use the two following chirp rates: ${\mu }_i^{\left(1\right)}=i\frac{2\mu }{N_{\mathrm{sat}}}$ and ${\mu }_i^{\left(2\right)}=2\mu -{\mu }_i^{\left(1\right)}$. The first one is used for $t\le T_{\mathrm{c}}/2$, and the other one for $T_{\mathrm{c}}/2<t\le T_{\mathrm{c}}$.

3. Signal Processing and Design

In this section, we show the receiver architecture and processing as well as the signal design of the proposed CSS-based PNT signal. Specifically, Section 3.1 deals with the pilot component and the design of the chirp period, whereas Section 3.2 deals with the data component and data transmission capabilities. Before going into detail, it is important to describe the receiving process of a CSS signal as given in (1), that is, the de-chirp process. The de-chirp process is illustrated in Figure 1, and it consists of mixing the received signal with the corresponding local replica and looking for the frequency of the maximum value of the resulting fast Fourier transform (FFT). This process is useful to receive a CSS signal and to estimate the data symbol when the signal is synchronized. Furthermore, this process is the cornerstone block for the design of both the pilot component used for ranging and synchronization [4,11].

3.1. Pilot Component

For the design process of the pilot component of a PNT system, we refer the reader to the study logic followed in [11]. This study looks for the shortest chirp period possible in order to minimize complexity. Unfortunately, we must fix a chirp period large enough to satisfy different requirements in terms of different KPIs. In particular, the KPIs that drive the design of the pilot component are the sensitivity and the accuracy. Since the target design is the complexity, we should look for the minimum chirp period ($T_{\mathrm{c}}$) that provides the target sensitivity. Then, with this fixed chirp period, the ranging accuracy can be evaluated. Recall that the pilot component uses a BOK-chirp signal, so the acquisition and estimation blocks will deal with 4 de-chirp processes as the one in Figure 1 [11].

In this section, we show the results of the sensitivity analysis useful to design the chirp period and further evaluate the performance of the data component. For the analysis of the accuracy performance, we refer to [11]. For the sensitivity, we define a sensitivity performance given by the probabilities of false alarm (PFA) and detection (PD) of the acquisition module, e.g., PD ≥ 0.9 when PFA = 10${}^{-5}$. Then, the main target of a sensitivity analysis is to find the minimum chirp period that provides the target sensitivity performance for different values of carrier-to-noise ratio (CN0), constellation size ($N_{\mathrm{sat}}$), and visible satellites ($N_{\mathrm{vis}}$). For the results shown in this paper, we will consider $\{N_{\mathrm{sat}},N_{\mathrm{vis}}\}=\{50,5\}$ satellites. 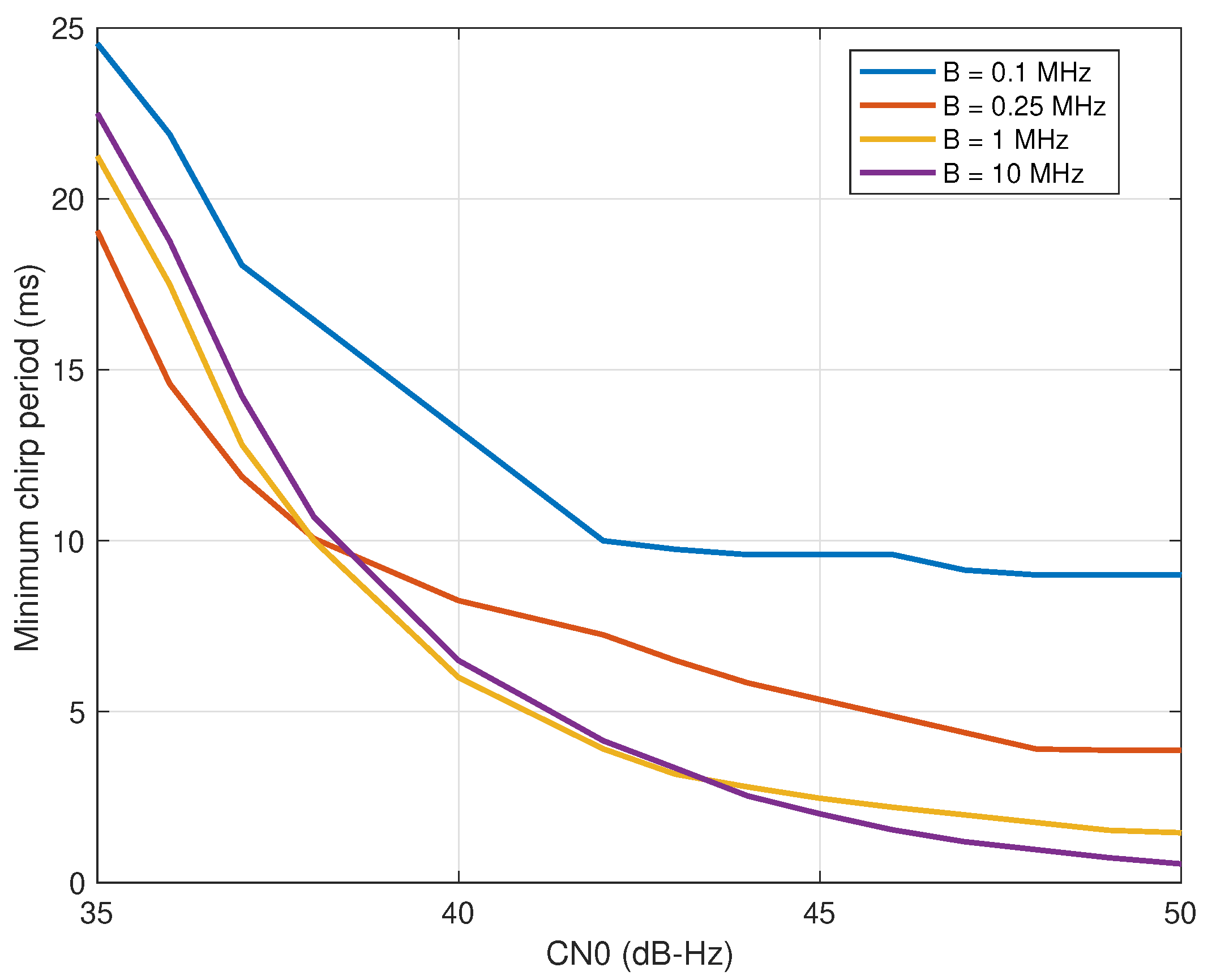An important analysis for the design of the CSS signal is the trend of $T_{\mathrm{c}}$ as a function of CN0. For instance, Figure 2 shows this analysis in the range of CN0 $=[35,50]$ dB-Hz and different bandwidths in the range of 100 kHz to 10 MHz. We take these results as a reference for the analysis of the data component. More details are given in [11].

3.2. Data Component

Let us focus now on the signal processing and design of the data component of a PNT system. First of all, it is important to note that the primary goal of a PNT signal is the ranging capabilities needed to obtain the user’s PNT solution. Therefore, the signal design parameters should be optimized, targeting the sensitivity and accuracy performance required for the (pilot) ranging component. Data dissemination capabilities are dependent on the system. For instance, for standalone GNSS receivers [18], a very small amount of data is needed to solve PNT (e.g., 50 bps is enough for GPS L1/CA), but a larger amount of data is needed for an SBAS receiver [14] (e.g., 250 bps for SBAS L1). Furthermore, different requirements are needed in terms of data latency, data rate, or quality depending on the application [14]. When targeting low-complexity GNSS, we should follow the same signal design followed in [11]; that is, in this section, we consider a chirp period design given by the sensitivity analysis (see Figure 2). Then, we define the relevant KPIs for the data component, namely, the bit error rate (BER) and achievable bit rate, $R_{\mathrm{b}}$. We do so for two different CSS modulations: the BOK- and FSK-CSS signals.

3.2.1. Bit Rate

To quantify the amount of data we can transmit over a CSS signal, we need to evaluate the number of bits transmitted per chirp period. This depends on the selected CSS modulation, e.g., BOK-CSS transmits one bit per (symbol) chirp period. Meanwhile, with a FSK-CSS signal, we work with a constellation of $M=2^{\mathrm{SF}}$ symbols, with $\mathrm{SF}$ as the spreading factor. The spreading factor denotes the number of bits per chirp period, and in a LoRa-like manner, it is given by [19]

$$\mathrm{SF}\doteq {log}_2\left(B{T}_{\mathrm{c}}\right),$$

(6)

where $T_{\mathrm{c}}$ is the chirp period, denoting the symbol duration and selected to achieve sensitivity performance. Then, the BOK- and FSK-CSS bit rates are respectively given by

$$R_{\mathrm{b}}^{\left(b\right)}\doteq \frac{1}{T_{\mathrm{c}}}\mathrm{and}{R}_{\mathrm{b}}^{\left(f\right)}\doteq \frac{\mathrm{SF}}{T_{\mathrm{c}}}.$$

(7)

3.2.2. Bit Error Rate (BER)

For the evaluation of the BER of the considered CSS modulations, we use available formulas in the literature. On the one hand, the BER of BOK-CSS can be evaluated as follows [20]:

$${\mathrm{BER}}_{\mathrm{BOK}}=\frac{1}{2}\mathrm{erfc}\left(\sqrt{0.25·\mathrm{MSI}·\mathrm{CN}0·T_{\mathrm{c}}}\right),$$

(8)

with $\mathrm{erfc}(·)$ as the complementary error function and $\mathrm{MSI}$ as the multisatellite interference accounting for the interference between satellites, as given in [11]. On the other hand, the BER for an FSK-CSS signal is approximated as [21]

$${\mathrm{BER}}_{\mathrm{FSK}}\approx \frac{1}{4}\mathrm{erfc}\left(\sqrt{\mathrm{MSI}·\mathrm{CN}0·T_{\mathrm{c}}}-\gamma (B,T_{\mathrm{c}})\right),$$

(9)

with $\gamma (B,T_{\mathrm{c}})=\sqrt{0.693·{log}_2\left(B{T}_{\mathrm{c}}\right)+0.577}$.

4. Performance Analysis

In this section, we provide the numerical analysis to evaluate the performance of the considered CSS signal in this paper. Recall that the performance evaluation of the pilot component was already studied in [11]. In this section, we focus on the performance of the data component and its relationship with the pilot component. To do so, we first provide in Section 4.1 the analysis of the achievable data rate for the two considered modulations (i.e., BOK- and FSK-CSS). Second, Section 4.2 studies the BER for the two considered modulations. For these two analyses, we consider different bandwidth and CN0 values. Furthermore, to link the analysis of the data component with the pilot component, we consider the sensitivity analysis given in the left plot of Figure 2 as a reference for the design of the chirp period and the corresponding MSI as computed in [11].

4.1. Bit Rate Analysis

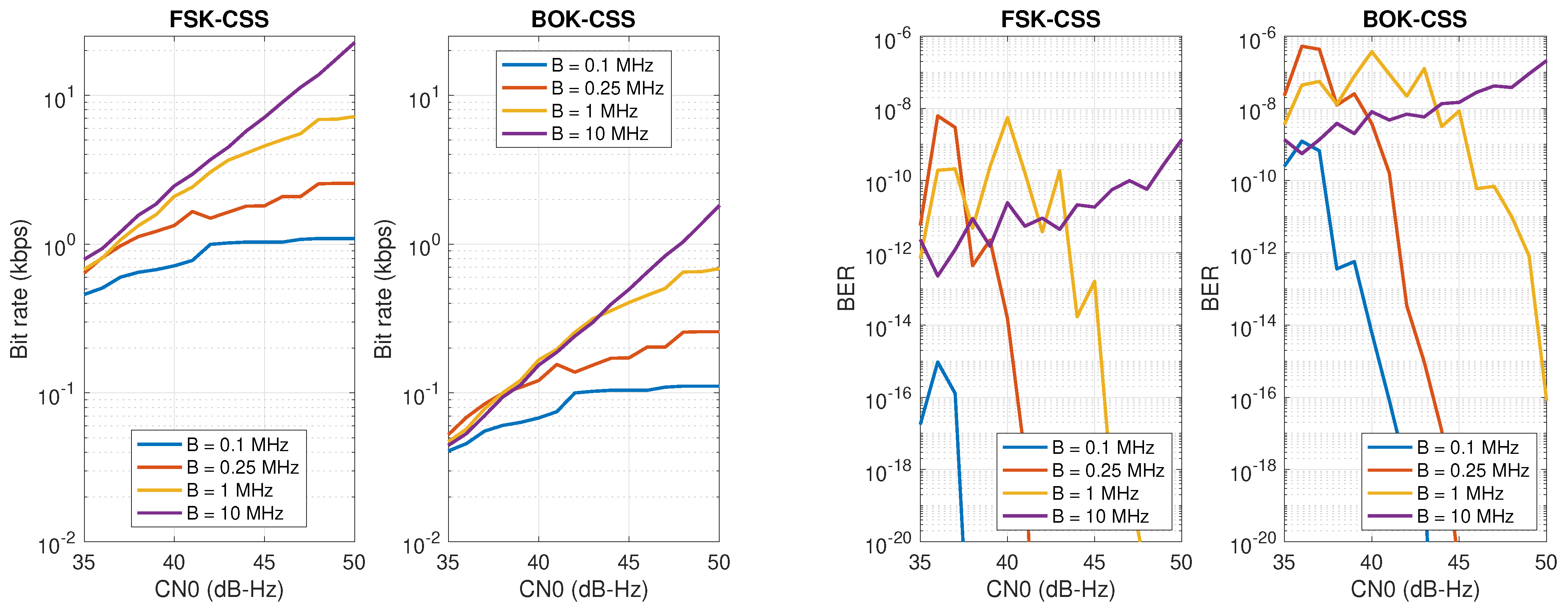
The analysis of the bit rate for the two considered modulations is shown in the left plot of Figure 3. For both modulations, as expected, we obtain an improvement of the achievable bit rate with the increment of CN0. We see that the bit rate moves to a saturation level at a given CN0. For instance, in the left plot, we see a saturation level of 1 kbps at 42 dB-Hz for the $B=0.1$ MHz curve (i.e., blue curve). Both the saturation level and the CN0 value at which it is reached are increased with the bandwidth value. The second observation we can extract from the left plot of Figure 3 is that we obtain less and less gain in bit rate for larger bandwidths. For instance, from $B=0.1$ MHz to $B=0.25$ MHz, we obtain an improvement in bit rate that is proportional to the bandwidth increment (i.e., ×2.5). However, the improvement with $B=10$ MHz is just ×20 bit rate (instead of ×100) with respect to $B=$ 0.1 MHz. Finally, another important point extracted from the results of bit rate is the difference between achievable values for FSK- and BOK-CSS. The former provides an improvement of 1 order of magnitude for all bandwidth and CN0 values.

4.2. BER Analysis

The evaluation of the BER for the two considered modulations is shown in the right plot of Figure 3. In both cases, the design of the chirp period is given by the sensitivity analysis as given in Figure 2. First, for both modulations, for a given CN0 value, we obtain an improvement of the BER when increasing the chirp period, $T_{\mathrm{c}}$. Note from Figure 2 that $T_{\mathrm{c}}$ increases as the bandwidth value is reduced. Second, analogously, the narrower the bandwidth value, the better BER we obtain at a given CN0 value. Finally, from the results of the right plot of Figure 3 for a given bandwidth and CN0 value, we see an improvement of FSK-CSS with respect to BOK-CSS in terms of BER. The improvement varies with the bandwidth value, but we obtain values ranging from 2 to 7 orders of magnitude. The results provided in this section for the data component are very interesting for a practical implementation of a PNT signal. This is so for both FSK- and BOK-CSS signals. The reason is that they provide a good demodulation performance in comparison with current GNSS signals. Actually, the BER values obtained in this section could be modified in order to reach higher values by using smaller $T_{\mathrm{c}}$ values and then providing higher bit rates than in the current configuration. Unfortunately, by doing so, we would incur a modification of the sensitivity performance to a poorer level. Finally, we have not considered in this section the application of channel coding techniques that may allow better demodulation performance, and thus a better achievable bit rate for a given CN0 value.

5. Discussion

This work has investigated the use of CSS for PNT. This allowed us to show the main challenges and KPIs useful for the design of a CSS-based PNT signal to be operated in LEO constellations and targeting low complexity. Since a PNT signal is equivalent to a joint ranging and communication signal, during the elaboration of the PNT signal design, we are evaluating the ranging and communication capabilities of the signal. Note that today GNSS technology is power hungry in the sense that it needs a high computational load, so the design of a CSS-based PNT signal might provide the solution to this problem. Furthermore, we see a trend of LEO-PNT systems. Unfortunately, the power consumption problem of GNSS is aggravated when moving from MEO to LEO. The reason is that the acquisition search space is increased in LEO due to the increased Doppler frequency with respect to MEO. In this paper, we have shown the different challenges and how to solve them for the design of a low-complexity LEO-PNT signal based on CSS. The first challenge comes when dealing with the estimation of the triple needed for PNT (time delay, Doppler, data) from the CSS signal. To do so, a pilot/data scheme is proposed based on a BOK-CSS and FSK structure for the pilot (i.e., time delay and Doppler estimation) and data (i.e., data demodulation) components, respectively. The second challenge to be dealt with is the design of an MSA scheme useful for PNT. Different schemes can be considered based on two main parameters of the CSS signal: the chirp rate and initial frequency. The performance analysis of the data component is given when linked with the design of the pilot component. The link is given by the design of the chirp period according to the sensitivity performance. The achievable data rate and BER of the considered modulations have been analyzed. Based on the results analyzed in this paper, we see how the proposed CSS signal is a good candidate for a PNT signal. First, it provides valuable results to be operated in a PNT system. For instance, as shown in previous works, it provides accuracies on the level of meters. Furthermore, we show in this paper achievable data rates in the order of tens of kbps. These are metrics of interest for a PNT system. On the other hand, we see that the CSS signal provides a better trade-off between ranging accuracy and achievable data rate than traditional DSSS signals used in GNSS. Note that current GNSSs provide accuracies in the order of meters or tens of meters with just a few tens of bps.