Semiparametric Block Bootstrap Prediction Intervals for Parsimonious Autoregression †
Abstract
:1. Introduction
2. Semiparametric Block Bootstrap Prediction Intervals
2.1. Iterated Block Bootstrap Prediction Intervals
- Save the residual of the backward regression given in Equation (8).
- Let b denote the block size (length). The first (random) block of residuals iswhere the index number is a random draw from the discrete uniform distribution between 1 and For instance, let and suppose a random draw produces then In this example the first block contains three consecutive residuals starting from the 20th observation. By redrawing the index number with replacement we can obtain the second block the third block and so on. We stack up these blocks until the length of the stacked series becomes denotes the t-th observation of the stacked series.
2.2. Direct Block Bootstrap Prediction Intervals
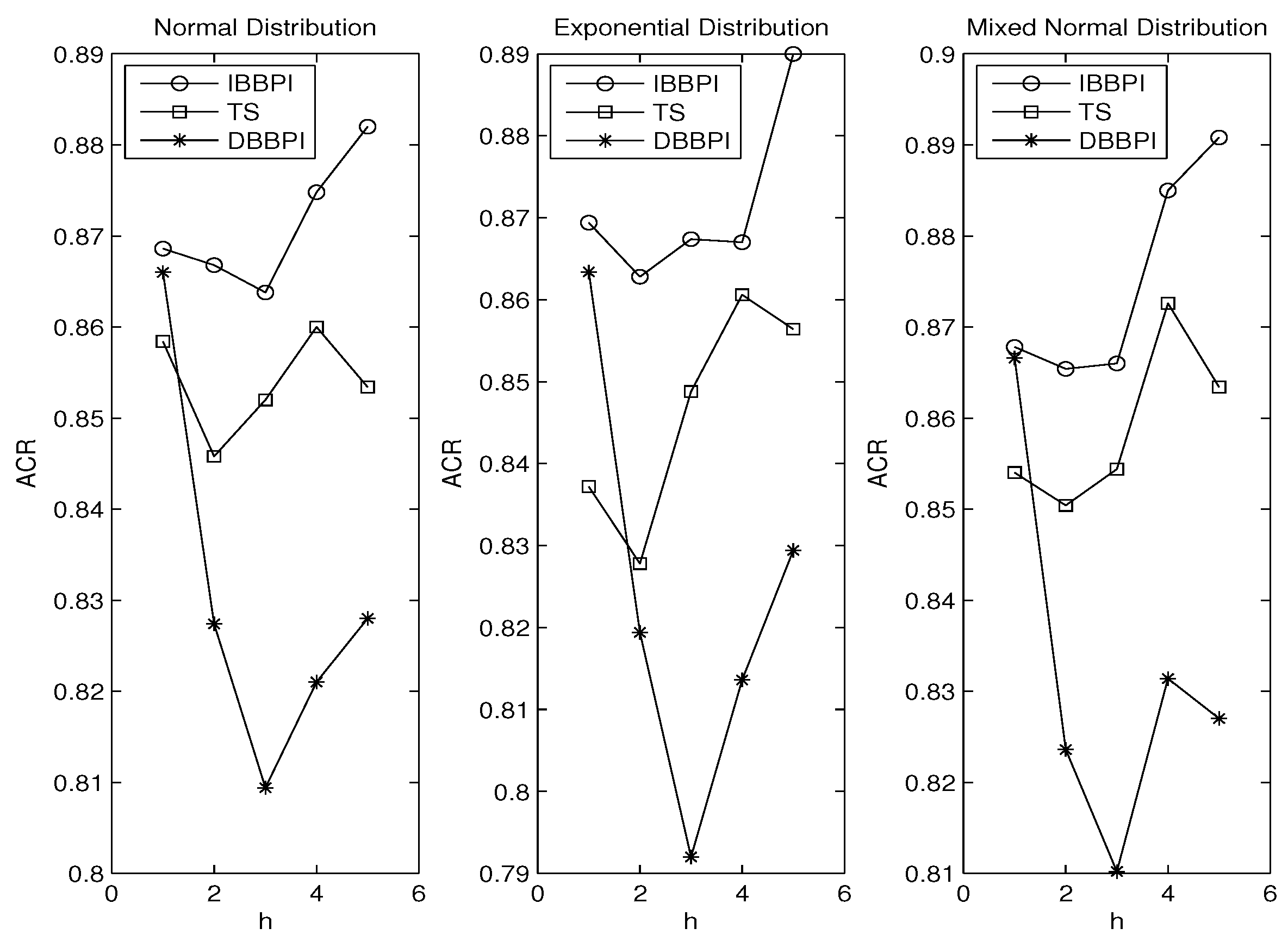
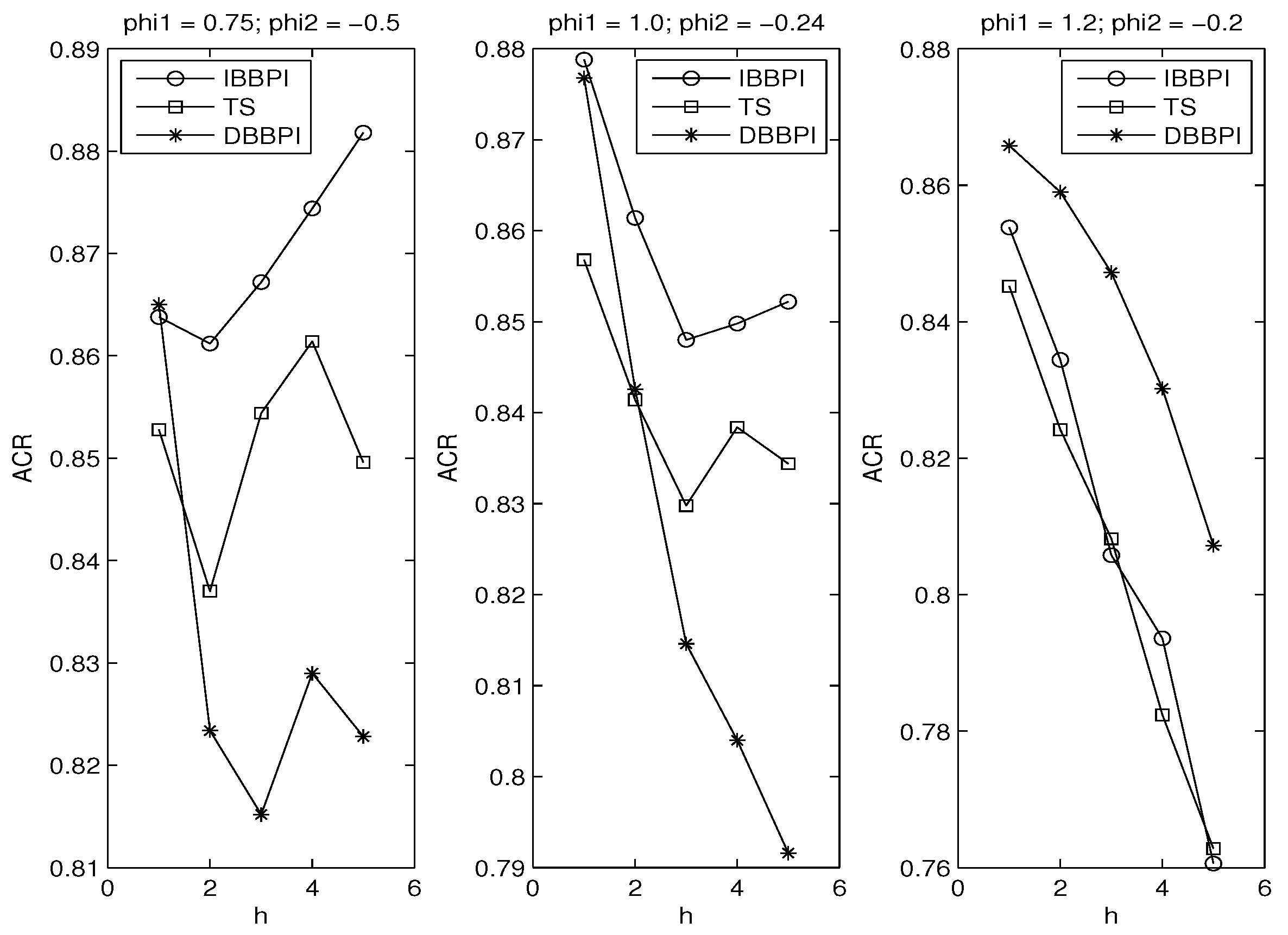
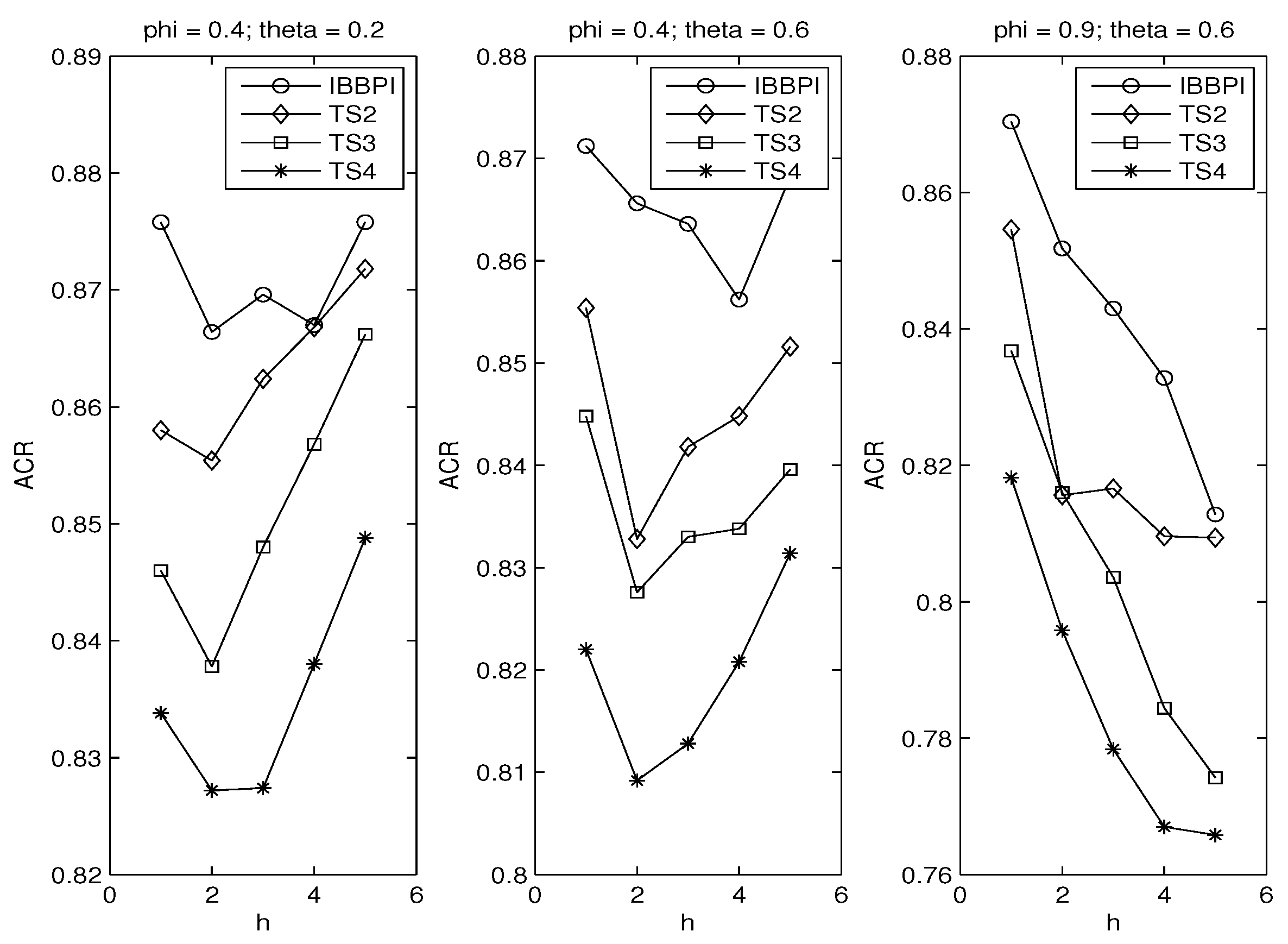
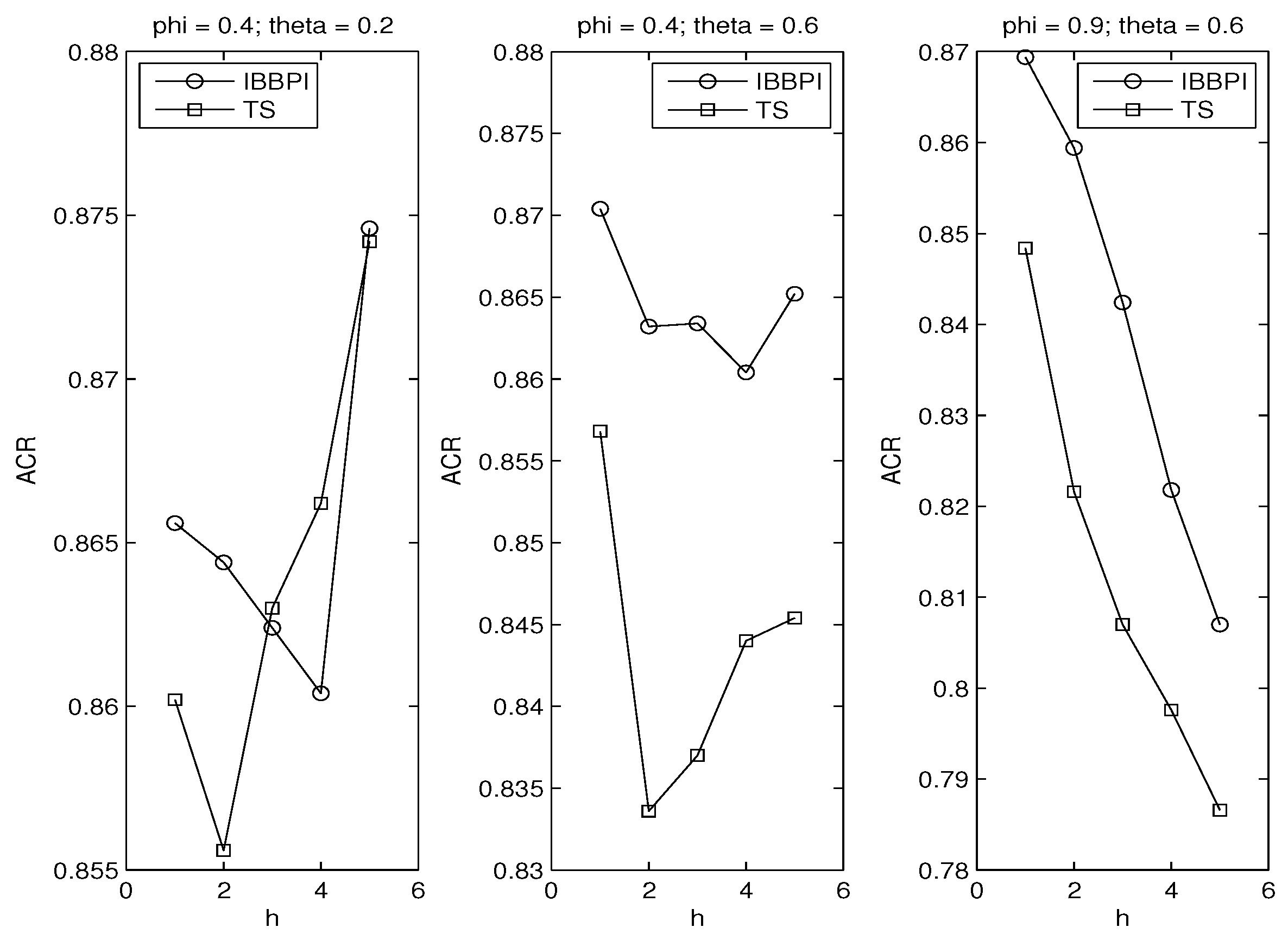
3. Monte Carlo Experiment
3.1. Error Distributions
3.2. Autoregressive Coefficients
3.3. Principle of Parsimony
4. Conclusions
References
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Thombs, L.A.; Schucany, W.R. Bootstrap prediction intervals for autoregression. J. Am. Stat. Assoc. 1990, 85, 486–492. [Google Scholar] [CrossRef]
- Enders, W. Applied Econometric Times Series, 3rd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Cochrane, D.; Orcutt, G.H. Application of least squares regression to relationships containing auto-correlated error terms. J. Am. Stat. Assoc. 1949, 44, 32–61. [Google Scholar]
- Politis, D.N.; Romano, J.P. The Stationary Bootstrap. J. Am. Stat. Assoc. 1994, 89, 1303–1313. [Google Scholar] [CrossRef]
- Masarotto, G. Bootstrap prediction intervals for autoregressions. Int. J. Forecast. 1990, 6, 229–239. [Google Scholar] [CrossRef]
- Grigoletto, M. Bootstrap prediction intervals for autoregressions: Some alternatives. Int. J. Forecast. 1998, 14, 447–456. [Google Scholar] [CrossRef]
- Clements, M.P.; Taylor, N. Boostrapping prediction intervals for autoregressive models. Int. J. Forecast. 2001, 17, 247–267. [Google Scholar] [CrossRef]
- Kim, J. Bootstrap-after-bootstrap prediction intervals for autoregressive models. J. Bus. Econ. Stat. 2001, 19, 117–128. [Google Scholar] [CrossRef]
- Kim, J. Bootstrap prediction intervals for autoregressive models of unknown or infinite lag order. J. Forecast. 2002, 21, 265–280. [Google Scholar] [CrossRef]
- Staszewska-Bystrova, A. Bootstrap prediction bands for forecast paths from vector autoregressive models. J. Forecast. 2011, 30, 721–735. [Google Scholar] [CrossRef]
- Fresoli, D.; Ruiz, E.; Pascual, L. Bootstrap multi-step forecasts of non-Gaussian VAR models. Int. J. Forecast. 2015, 31, 834–848. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Block Bootstrap Prediction Intervals for Parsimonious First-Order Vector Autoregression. J. Forecast. 2021, 40, 512–527. [Google Scholar] [CrossRef]
- Künsch, H.R. The Jackknife and the Bootstrap for General Stationary Observations. Ann. Stat. 1989, 17, 1217–1241. [Google Scholar] [CrossRef]
- Shaman, P.; Stine, R.A. The bias of autoregressive coefficient estimators. J. Am. Stat. Assoc. 1988, 83, 842–848. [Google Scholar] [CrossRef]
- Booth, J.G.; Hall, P. Monte Carlo approximation and the iterated bootstrap. Biometrika 1994, 81, 331–340. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall: London, UK, 1993. [Google Scholar]
- De Gooijer, J.G.; Kumar, K. Some recent developments in non-linear time series modeling, testing, and forecasting. Int. J. Forecast. 1992, 8, 135–156. [Google Scholar] [CrossRef]
- Hartigan, J.A.; Hartigan, P.M. The DIP test of unimodality. Ann. Stat. 1985, 13, 70–84. [Google Scholar] [CrossRef]
- Ing, C.K. Multistep Prediction in Autogressive Processes. Econom. Theory 2003, 19, 254–279. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J. Semiparametric Block Bootstrap Prediction Intervals for Parsimonious Autoregression. Eng. Proc. 2021, 5, 28. https://doi.org/10.3390/engproc2021005028
Li J. Semiparametric Block Bootstrap Prediction Intervals for Parsimonious Autoregression. Engineering Proceedings. 2021; 5(1):28. https://doi.org/10.3390/engproc2021005028
Chicago/Turabian StyleLi, Jing. 2021. "Semiparametric Block Bootstrap Prediction Intervals for Parsimonious Autoregression" Engineering Proceedings 5, no. 1: 28. https://doi.org/10.3390/engproc2021005028
APA StyleLi, J. (2021). Semiparametric Block Bootstrap Prediction Intervals for Parsimonious Autoregression. Engineering Proceedings, 5(1), 28. https://doi.org/10.3390/engproc2021005028




