1. Introduction
Adjustment calculus offers a rich toolbox of statistical models and procedures for parameter estimation and hypothesis testing based on given numerical observations (cf. [
1]). Such models usually consist of a deterministic functional model (e.g., a linear model describing some trend function), a correlation model (e.g., in the form of a variance-covariance matrix or an autoregressive (AR) error process), and a stochastic model (i.e., a probability distribution of the observation errors or the innovations of the AR error process). The stochastic model is often taken to be some multivariate normal distribution, which, however, easily leads to erroneous estimation results if the observations are afflicted by outliers. To take outliers into account, the normal distribution can be replaced by some outlier distribution, for example, a heavy-tailed t-distribution (cf. [
2]). A multivariate time series model, including a nonlinear functional model and an autoregressive observation error model with t-distributed innovations, was suggested and investigated in [
3] and [
4]. A shortcoming of that model is that it does not include prior knowledge about the parameters of the functional, correlation or stochastic model, the information about which may readily be available. Therefore, the current paper describes a Bayesian extension of that time series model, which can be expected to result in more robust and more accurate parameter estimates (cf. [
5]).
A general Bayesian estimation approach in the specific context of models based on the t-distribution was introduced by [
6]. Due to the complexity of such a model, the posterior density function must be approximated numerically or analytically. For numerical approximation, Monte-Carlo (MC) simulation and, in particular, Markov-Chain Monte-Carlo (MCMC) methods, which are suitable also for multivariate distributions, have been applied routinely (cf. [
7]). In particular, the Gibbs sampler and the Metropolis–Hastings algorithm have been employed for (non-robust) Bayesian estimation of the parameters of a linear functional model with autoregressive moving-average (ARMA) and normally distributed errors [
8]. MCMC methods have also been applied in the context of the robust Bayesian estimation of ARMA models [
9] and AR models [
10], with one additional (directly observed) mean parameter in the functional model. In both studies, outliers within the auto-correlated errors and within the uncorrelated innovations were modeled as normally distributed random variables with variances inflated by unknown multipliers. Thus, the stochastic error model was based on a discrete mixture of normal distributions, not on the t-distribution. To incorporate an automatic model selection procedure regarding the AR/ARMA model into the adjustment, the preceding studies also included unknown index parameters, taking the value 0 in case the corresponding AR (or MA) coefficient is 0 (or not significant) and taking the value 1 otherwise. Prior distributions for all of the parameter groups and the likelihood function for the data were fixed, and sampling distributions were then derived in order to obtain a numerical approximation of the posterior distribution for all the unknowns. In [
11], an MCMC-based computational algorithm was proposed, to facilitate Bayesian analysis of real data when the error structure can be expressed as a p-order AR model.
The paper is organized as follows: First, the Bayesian multivariate time series model with AR and t-distributed errors is described in detail in
Section 2. It is shown how the generic deterministic functional model, the AR process and the t-distribution model are first combined to a likelihood function and how prior information about the model parameters to be estimated is taken into account by means of a specified prior density. Here, we denote unknown parameters with Greek letters, random variables with calligraphic letters, and constants with Roman letters. Furthermore, we distinguish between a random variable (e.g.,
) and its realization (
). Matrices are shown, as usual, as bold capital letters and vectors as bold small letters.
Section 3 outlines an MCMC algorithm for determining the posterior density of the unknown parameters of the functional model, the coefficients of the AR process and the scale parameter, as well as the degrees of freedom of the t-distribution. In
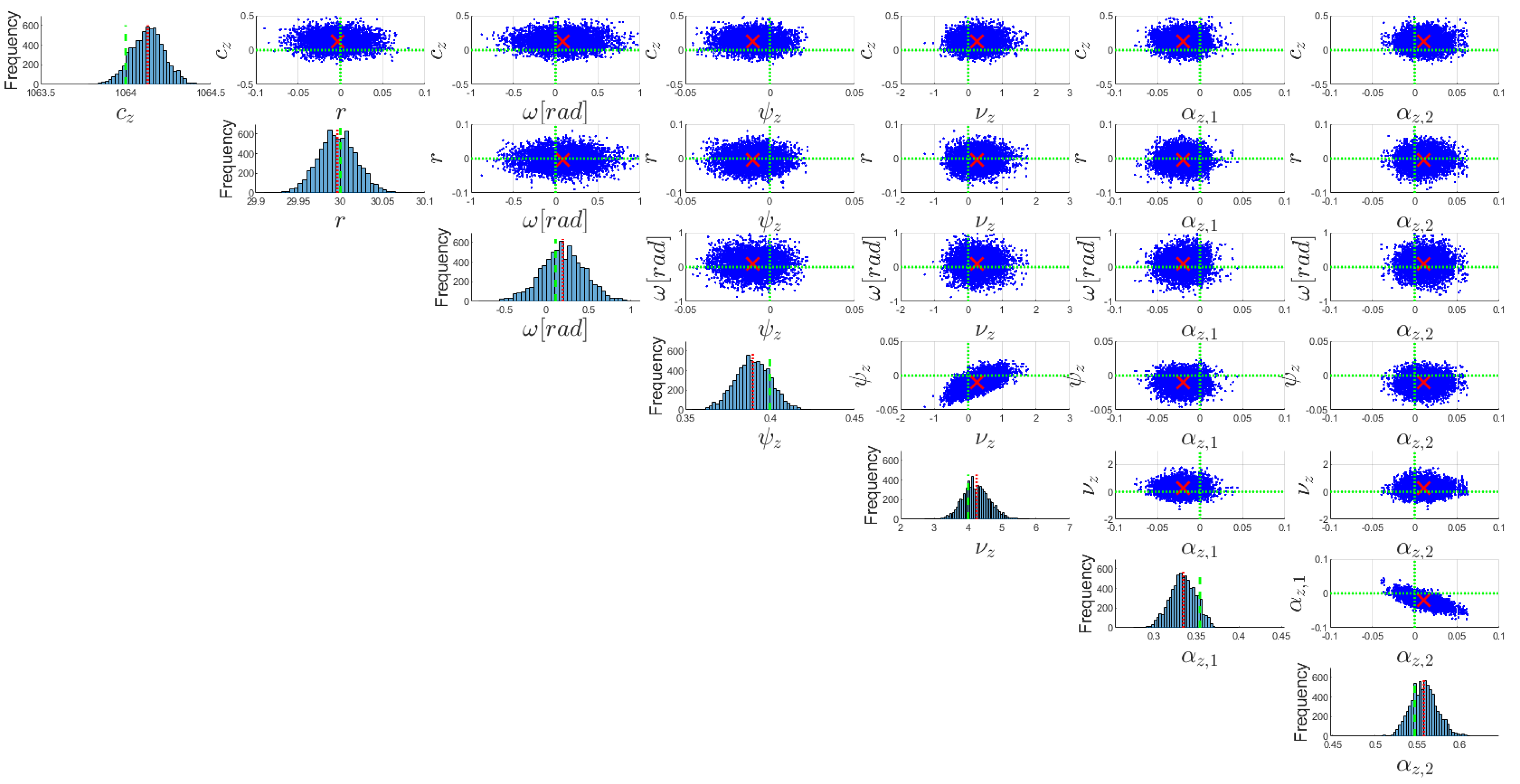
Section 4, a time series model for GNSS observations of a circle in 3D is proposed, and the results of a Monte Carlo simulation are discussed. These findings are used to evaluate the performance of the implemented Metropolis–Hastings-within Gibbs algorithm in this scenario.
2. The Bayesian Time Series Model
We assume that an
N-dimensional time series
is observed at equi-spaced time instances
t without data gaps. The observation model consists of the three interconnected model components,
where (
1) defines the “observation equations”, (2) the “error equations” and (3) defines the probability distribution of the innovations. The parameters of this observation model are combined within the vector,
with
On the one hand, the parameters
are treated as variables of the likelihood function
, defined by the observation model (
1)–(3). On the other hand, the parameters
are viewed as a realization of a random vector
, having a specified pdf independent of the observables. According to the Bayes theorem, this prior density
and the likelihood function
are connected to the posterior density
via proportionality relationship
which serves as the foundation of the inference of the parameters and the adjustment of the observations. The details of this model are described in the following.
The observation equations: Equation (
1) reflects the idea that geodetic measurements
are approximated by a “deterministic” model using mathematical functions
, which are assumed to be partially differentiable. The index
k refers to the time series surveyed by the
kth sensor or sensor component, and the time instances
are the same for all sensors. In some applications, the functional model
takes the form
of a “linear model”, where
denotes the design matrix and has a full rank. Since geodetic observables can generally not be modeled using a deterministic model alone, random deviations
are added to absorb the remaining effects. It is assumed that the instruments used to survey the observables are calibrated, so that no systematic errors occur. Thus, the expected values of the random deviations are assumed to be 0.
The error equations: Equation (2) is included to take account of auto-correlations within each of the
N time series. Since the different sensors or sensor components may have different noise characteristics, AR processes, with individual orders
and sets of coefficients
, are selected. The noise characteristics are assumed to be constant throughout the measurement period. For practical purposes, the AR processes considered are therefore required to be (asymptotically) covariance-stationary. The random variables
are referred to as “innovations”. Since the observation window is finite, ranging from
, the error equations involve errors at times
. To ensure asymptotic covariance-stationarity and the computability of the recursive equations, these quantities are set as equal to 0 (cf. [
12]). This initial distortion of the AR process fades out as the process advances in time.
The stochastic model: The innovations of an AR process are usually assumed to be Gaussian white noise. Since the assumption of normal distributions is unrealistic in some geodetic applications, for example, due to outliers, the heavy-tailed t-distributions are employed here. These are defined by the probability density function (pdf),
where
is the gamma function. Since the expected values of the random deviations
should be 0, we can also restrict the location parameter
to 0. Since the noise of different sensors or sensor components may exhibit different levels of variance and outliers, each time series involves a t-distribution with individual scale parameter
and degree of freedom (df)
. It should be mentioned that the alternative usage of a multivariate t-distribution (as defined in [
2]) involves a single df and would therefore not allow for the modeling of distinct outlier characteristics within the different time series.
The likelihood function: A likelihood function
can be obtained by combining the observation Equation (
1), the error Equation (2) and the stochastic model of the innovations (3). To do so, the well-known method of conditional likelihoods in connection with AR processes with various forms of non-Gaussian innovations is applied (cf. [
13,
14,
15]). Assuming the AR processes to be invertible, the error Equation (2), in terms of their numerical realizations, can be rewritten as “innovation equations,”
As the errors
contained in the observation equations (
1) can be expressed as
the innovation equations (
12) become
The conditional likelihood function is then obtained as the product of the univariate pdf (
11), evaluated at all the stochastically independent innovations
with location
, associated scale factor
and df
, that is,
For the purpose of maximum likelihood (ML) estimation, the logarithm of this likelihood function is easier to handle (see [
3]). In that contribution, a computationally convenient ML estimation of the model parameters was achieved by rewriting the t-distributions as conditional normal distributions with latent variables; these variables play the role of weights in an iteratively reweighted least-squares algorithm. As the main innovation of the current contribution, the likelihood function (
15) is incorporated into a Bayesian model instead, which is described in the following.
The Bayesian model: In this contribution, both informative and non-informative prior information is considered. The result of using a fully non-informative prior is that the posterior density follows directly from the likelihood function. In the case of an informative prior, a joint pdf must be specified for the random vector
. This task is simplified by the assumption of stochastic independence of the parameter groups
,
,
and
, so that the factorization property,
holds. Consequently, individual prior densities can be specified for these parameter groups. As the prior density of
depends on the selected functional model
, its specification is fixed after the introduction of the application example in
Section 4. In contrast, the prior densities for
,
and
do not depend on the choice of the functional model but mainly on the precision of the sensors or instruments employed. In the case that no prior information is available for the employed sensors or instruments, it is still possible to define prior densities for these three groups of parameters. Due to the assumption, in connection with the error Equation (2) and the stochastic model (3), that the
N time series is stochastically independent, the prior density can be further simplified to
Consequently, as far as the parameters
and
are concerned, only univariate prior densities
and
need to be specified. When it is known that the scale factor
is between
and
, the prior density defining the continuous uniform distribution
can be used as a weak form of prior information. The specification of the prior for the df
can be based, on the one hand, on the requirement
, so that the variance of the t-distributed random variables is defined. On the other hand, the t-distribution is practically indistinguishable from a normal distribution for dfs greater than 120 (cf. [
16]), so that the upper limit
can be fixed. In the absence of further information about the dfs, the prior density defining the continuous uniform distribution
is reasonable. The auto-correlations of a time series may, for instance, be induced by calibration corrections within the measurement device, by movements of the measured object, or by a combination of the two effects. Therefore, a general definition of the prior density of the AR coefficients is not trivial. For this reason, a non-informative prior density is specified under the additional assumption that all of the AR coefficients are stochastically independent.
3. The Developed MCMC Algorithm
Because of the use of the Student distribution for the white measurement noise (Equation (
15)), an analytical solution of the posterior density based on the Bayes theorem (Equation (
9)) is not possible, so it can only be solved numerically. The general solution approach is based on generating a so-called Markov Chain for the unknown posterior density using the MCMC method. MCMC algorithms are commonly used in all fields of statistics because of their versatility and generality. When an MCMC method is applied to solve the posterior density function given in (
9), it is usually realized with a Gibbs sampler. An implementation of a Gibbs sampler relies on the availability of the complete conditional pdfs of all parameters of interest in our particular problem (cf. Equation (
4)). However, the complete conditional pdfs of all parameters of interest are not readily available. In such cases, a Metropolis–Hastings (MH) method can be incorporated within a Gibbs sampler to draw samples from the parameters, the full conditional pdf of which cannot be analytically determined. In this paper, we demonstrate the development of such an algorithm, known as Metropolis–Hastings-within Gibbs. In this algorithm, the Gibbs sampler is used to generate the Markov Chain for
, and within the Gibbs sampler the MH algorithm is used to generate random numbers. For a clearer presentation, the solution algorithm is encapsulated by two separate functions. For the Gibbs sampler, the outer function is given by,
where
is the length of the MCMC. Such a Markov chain ensures the convergence of the distribution of the samples to the target distribution after a few burn-in periods
[
17]. We observe that the full conditional pdf shown in (
20) does not fit to any known pdf and, therefore, we cannot directly draw samples from it.
However, there are two challenges to calculating the conditional posterior densities. The first challenge is that it results from the likelihood function and the prior density. Consequently, changing the distributional assumption for the prior density results in a new conditional posterior density. While this challenge can be overcome with a small amount of effort, the second challenge is much more fundamental. For the calculation of the conditional posterior densities, several integrals have to be solved and this may not be analytically possible. To overcome these challenges, the MH algorithm is used to draw the required random numbers. The general algorithm for drawing a random number
from the posterior density
follows from the following steps:
where
m in Equation (22) denotes the length of the parameter vector. The results of the Metropolis–Hastings-within Gibbs are
random realizations of the unknown parameters
,
,
and
from the posterior density
. The estimated values
for the unknown parameters with their variance–covariance matrix (VCM) result from (cf. [
5]):