Aquila-Based Model Predictive Control of an Adapted Fridge Display Case Model for Vaccine Preservation ^†

Abstract

Temperature excursions and vaccine freezing are the results of poor temperature control systems used in the vaccine cold chain. The use of medium-temperature fridges due to inadequate vaccine refrigerators has had great negative impacts on the coverage of national immunization programs in developing countries, as many vaccines are often wasted due to loss of vaccine potency, thereby leading to wastage of investment. To surmount these challenges, an adapted fridge display case model using an Aquila-based model predictive control strategy for preserving vaccines at the correct temperature range of 2 °C and 8 °C is proposed. Temperature responses using an Aquila-based model predictive controller (AO-MPC) was compared with a proportional–integral–derivative (PID) controller. Simulation results show that AO-MPC has better capability in mitigating the problem of accidental freezing and temperature excursion by keeping the vaccine temperature at 5.8 °C, even in the presence of additive disturbances, while the PID controller has oscillations for about 4.5 h before settling at 8 °C. MATLAB 2020a was used to perform all simulations.

1. Introduction

Immunization is one of the most successful public health strategies now accessible since it helps avoid major illnesses and saves lives. Programs for immunization are among the most economical ways to avoid disease. The success of these programs significantly depends on how vaccines are handled and stored. Proper vaccine handling and storage practices can play a crucial part in enhancing the health of patients by ensuring that the injected vaccines maintain their efficacy and that vaccine waste is decreased [1]. However, it has been reported that 17% to 37% of healthcare providers expose vaccines to improper storage temperatures [2]. Vaccines are damaged by exposure to excessive cold, heat, and/or light. Most vaccines lose potency more quickly in the presence of heat, which shortens their shelf life, while freezing can deteriorate the vaccine and induce hairline fractures in the ampoule, vial, or pre-filled syringe, which may allow the contents to get contaminated. Effectiveness cannot be guaranteed for vaccines unless they have been stored at the correct temperature [3].

The phrase “vaccine cold chain” refers to the methods and tools used to keep vaccinations within the specified temperature range of +2 °C to +8 °C from the time of manufacture until the immunizations are given to people. A cold chain incident happens when vaccination is exposed to a temperature outside the acceptable range. [4,5]. A poor cold chain can result in a cumulative loss of potency of vaccines and ineffective vaccines can result in an increased risk of vaccine-preventable diseases. The World Health Organization (WHO) no longer recommends that freeze-dried vaccines be stored at extremely low temperatures because storing them at such temperatures is unnecessary. Instead, these vaccines should be kept in refrigeration and transported at +2° to +8 °C [6]. Despite the high-level advocacy for adequate and routine budgeting of cold chain expenses, most developing nations still face difficulties in realizing significant and sustained improvements in the vaccine cold chain due to large investments involved in equipment replacement. There is, therefore, a need to introduce technical innovations into the immunization programs, in order to reinvigorate the immunization efforts by achieving an improved cold chain that is capable of strengthening the immunization program [7].

Although the World Health Organization (WHO) and United Nations International Children’s Emergency Fund (UNICEF) provide up-to-date guidelines and procedures for proper vaccine storage—such as the use of ice packs and temperature monitoring and recording by the operator twice every twenty-four hours—they are often ignored or prone to human error. Other solution strategies, such as the development of new vaccines that are resistant to freezing and the use of phase change materials (PCM) are costly. The use of explorative super cooling technology for the prevention of freeze damage in vaccines was presented in [8]. Loss of vaccine emanating from accidental freezing was reduced by using temperature recorders in [9]; however, the risk of freezing still exists using the device. Cold chain systems in [10] still rely on the use of stem thermometers; however, they were unable to effectively detect temperature excursions that are needed to be prevented. The lack of efficient temperature control systems for thermo-sensitive vaccines remains one of the critical factors responsible for WHO’s inability to achieve routine global immunization solutions.

Model predictive controller (MPC) has been used for refrigeration system control in [11]; however, their implementation did not consider the use of optimization algorithms for improvement in system performance and violation of temperature constraints was reported. The smell agent optimization algorithm developed by [12] was used in [13] for a simple thermal system; however, the temperature responses are focused on food preservation and are not within the recommended temperature range required for vaccine preservation. Particle swarm optimization (PSO) for enhancement of refrigeration system control was reported in [14]; however, the system responses are unfit to be used for vaccination purposes. Therefore, the need for an optimal control methodology for medium-temperature vapour compression refrigerators, used in most clinics and hospitals in developing countries, that are specifically tailored towards proper vaccine storage application still remains a gap in the literature.

Therefore, this paper proposes a metaheuristic-based model predictive control strategy using Aquila optimizer to tune the parameters of the MPC in order to maintain the fridge temperature within the recommended bounds even in the presence of disturbances. Aquila optimizer is chosen due to its simple structure, high search efficiency, strong global exploration ability, and fast convergence speed.

The outline of this paper is as follows: Section 2 presents the fridge display case model, linear model predictive controller and Aquila optimization algorithm. Simulation results and discussions are presented in Section 3. Finally, Section 4 concludes the paper.

2. Materials and Methods

2.1. Dynamic Model of a Fridge Display Case

A fridge display case model is made up of the expansion valve and the evaporator whose dynamics are affected by both the temperature of the goods ($T_{goods}$), air temperature ($T_{air}$), and the temperature of the walls of the refrigerated space ($T_{wall}$) [15].

The formulation of the fridge display case model is based on lumped parameter analysis. The nonlinear model of the system is summarized as:

$${\dot{T}}_{goods}=-\frac{{UA}_{ga}}{{M_{goods}C}_{P_{goods}}}{T}_{goods}+\frac{{UA}_{ga}}{C_{P_{goods}}}{T}_{air}$$

(1)

$${\dot{T}}_{air}=\frac{{UA}_{ga}}{{M_{air}C}_{P_{air}}}{T}_{goods}+\frac{{UA}_{ga}+{UA}_{aw}}{{M_{air}C}_{P_{air}}}{T}_{air}+\frac{{UA}_{aw}}{{M_{air}C}_{P_{air}}}{T}_{wall}+\frac{{\dot{Q}}_{airload}}{{M_{air}C}_{P_{air}}}$$

(2)

$${\dot{T}}_{wall}=\frac{{UA}_{aw}}{{M_{wall}C}_{P_{wall}}}{T}_{air}+\frac{{UA}_{aw}+{UA}_{wr}\frac{M_{refrig}}{M_{refrigmax}}}{{M_{wall}C}_{P_{wall}}}{T}_{wall}+\frac{{UA}_{wr} (-4.35P_{suc}^2+29.20P_{suc}-51.20)}{{M_{wall}C}_{P_{wall}}{M}_{refrigmax}}{M}_{refrig}$$

(3)

$${\dot{M}}_{refrig}=V_p\left(\frac{M_{refrigmax}-M_{refrig}}{{\tau }_{fill}}\right)+(V_P-1)\left(\frac{{UA}_{wr}\frac{M_{refrig}}{M_{refrigmax}} (T_{wall}+4.35P_{suc}^2-29.20P_{suc}+51.20)}{\left(0.022P_{suc}^2-0.17P_{suc}+2.30\right).{10}^5}\right)$$

(4)

where ${UA}_{wr}={UA}_{wall\to refrigmax}$, ${UA}_{ga}={UA}_{goods\to air}$, ${UA}_{aw}={UA}_{air\to wall}$.

Derivation of the state-space model was achieved through linearization as shown below:

$$\dot{x}=Ax\left(t\right)+Bu\left(t\right)+Ed\left(t\right)$$

(5)

$$y\left(t\right)=Cx\left(t\right)+Du\left(t\right)$$

(6)

Therefore, the linearized system is given as:

$$\begin{gathered} \left[\begin{array}{c}\begin{array}{c}{\dot{T}}_{goods}\\ {\dot{T}}_{air}\end{array}\\ \begin{array}{c}{\dot{T}}_{wall}\\ {\dot{M}}_{refrig}\end{array}\end{array}\right]=A\left[\begin{array}{c}\begin{array}{c}{T}_{goods}\\ T_{air}\end{array}\\ \begin{array}{c}{T}_{wall}\\ M_{refrig}\end{array}\end{array}\right]+B\left[\begin{array}{c}{V}_p\\ P_{suc}\end{array}\right]+E\left[Q_{airload}\right] \\ \left[\begin{array}{c}{T}_{goods}\\ T_{air}\end{array}\right]=C\left[\begin{array}{c}\begin{array}{c}{T}_{goods}\\ T_{air}\end{array}\\ \begin{array}{c}{T}_{wall}\\ M_{refrig}\end{array}\end{array}\right]+D\left[\begin{array}{c}{V}_p\\ P_{suc}\end{array}\right] \end{gathered}$$

(7)

The system parameters used are given in

Table 1. This table shows the system parameters used which are derived from [15].

Parameter	Value	Unit
$M_{goods}$	1200	$\mathrm{k}\mathrm{g}$
$M_{air}$	125	$\mathrm{k}\mathrm{g}$
$M_{wall}$	180	$\mathrm{k}\mathrm{g}$
$M_{refrigmax}$	0.6	$\mathrm{k}\mathrm{g}$
${UA}_{goods\to air}$	600	$\mathrm{J}{\mathrm{s}}^{-1}{\mathrm{K}}^{-1}$
${UA}_{wall\to refrigmax}$	900	$\mathrm{J}{\mathrm{s}}^{-1}{\mathrm{K}}^{-1}$
${C_P}_{goods}$	3917	$\frac{\mathrm{J}}{\mathrm{k}\mathrm{g}·\mathrm{K}}$
${C_P}_{air}$	1000	$\frac{\mathrm{J}}{\mathrm{k}\mathrm{g}·\mathrm{K}}$
${C_P}_{wall}$	385	$\frac{\mathrm{J}}{\mathrm{k}\mathrm{g}·\mathrm{K}}$
${\tau }_{fill}$	40	s
${UA}_{air\to wall}$	500	$\mathrm{J}{\mathrm{s}}^{-1}{\mathrm{K}}^{-1}$
${UA}_{amb}$	60	$\mathrm{J}{\mathrm{s}}^{-1}{\mathrm{K}}^{-1}$
$T_{wall,0}$	−4.2442	°C
$M_{refrig,0}$	0.0669	$\mathrm{k}\mathrm{g}$
$P_{suc,0}$	1.4	$\mathrm{b}\mathrm{a}\mathrm{r}$

below:

Where, M_goods, M_air, M_wall and M_refrig denote the mass of goods, the mass of air in the display case, the mass of air in the evaporator wall and the mass of refrigerant in the evaporator respectively. Also, Cp_goods, Cp_air, and Cp_wall denote the specific heat capacities of goods, air, and evaporator wall, respectively. Then, UA_goods$\to$_air, UA_air$\to$_wall, UA_amb and UA_wall$\to$_refrigmax are the heat transfer coefficients between goods and air, the heat transfer coefficient between air and wall, the heat transfer coefficient of the ambient air and the heat transfer coefficient with the evaporator filled up. Moreover, τ_fill is the time to fill the evaporator when the valve is open and all variables with a subscript of ‘0’ represent a fixed work point value for that variable. Finally, V_p, P_suc, and Q_airload are the valve opening, suction pressure, and the heat flow rate from the ambient air to the air in the display case, respectively.

2.2. Linear Model Predictive Controller

Model predictive control (MPC) is an advanced algorithm that utilizes the dynamic model of the process to predict its future behaviour over a finite time horizon and compute an optimal control input that minimizes the cost function while satisfying the system constraint. It can be mathematically represented below:

$$min\left\{{\sum }_{k=0}^{N-1}{(\parallel y_{t+k}-r(t)\parallel }^2+\rho {\parallel u_{t+k}-u_r\left(t\right)\parallel }^2)\right\}$$

(8)

$$s.t.: x_{t+k+1}=f(x_{t+k},u_{t+k})$$

(9)

$$y_{t+k}=g(x_{t+k},u_{t+k})$$

(10)

$$u_{min}\le u_{t+k}\le u_{max}$$

(11)

$$y_{min}\le y_{t+k}\le y_{max}$$

(12)

$$x_t=x\left(t\right), k=0,\dots ,N-1$$

(13)

According to the receding horizon concept, the optimal sequence is gotten over N steps, while the first optimal control action u*(t) is used. New measurements/state estimates are gotten at time t + 1, and the process of optimization is repeated [16].

2.2.1. Objective Function

The objective function for the vaccine temperature control problem is formulated as integral square error due to its ability to eliminate large errors (in temperature deviations) quickly. It is given as:

$$f\left(x\right)=min{\sum }_{i=1}^N{{(T}_{air}-T_{ai{r}_{reference}})}^2$$

(14)

where $T_{ai{r}_{reference}}$ represents the acceptable temperature range for vaccine preservation, that is, the range of 2 °C to 8 °C.

The constraints are:

$$T_{air\text{\_}min}\le T_{air}\le T_{air\text{\_}max}$$

(15)

$$T_{goods\text{\_}min}\le T_{goods}\le T_{goods\text{\_}max}$$

(16)

$$V_{p\text{\_}min}\le V_p\le V_{p\text{\_}max}$$

(17)

$$P_{suc\text{\_}min}\le P_{suc}\le P_{suc\text{\_}max}$$

(18)

$${\dot{Q}}_{amb-air\text{\_}min}\le {\dot{Q}}_{amb-air}\le {\dot{Q}}_{amb-air\text{\_}max}$$

(19)

where all variables with a subscript ending with $min$ and $max$ represent the minimum and maximum values used for that variable. The MPC parameters chosen to be tuned in this research are the prediction horizon and the control horizon.

2.2.2. Aquila Optimizer

Aquila optimizer (AO) is a novel nature-inspired, population-based optimization algorithm. It uses the hunting strategies of Aquila birds to stochastically find solutions to engineering optimization problems. It starts with the population of candidate solutions (X) which lies between the upper bound (UB) and lower bound (LB) of the optimization problem.

$$X_{i,j}=r\mathrm{and}\times \left({UB}_j-{LB}_j\right)+{LB}_j, i=1, 2,\dots , N and j=1, 2, \dots , Dim$$

(20)

where X represents a set of candidate solutions at the current state, that are randomly generated by using Equation (20), X_i refers to the positions of the ith solution, N represents the total number of candidate solutions, and Dim represents the size of the problem dimension. Here, rand stands for a random number, LB_j is the jth lower bound and UB_j represents the jth upper bound. The detailed mathematical modelling is explained in Abualigah et al. [16].

3. Results and Discussions

Two-step inputs with an initial value (lower bound) of 2 °C and a final value (upper bound) of 8 °C were used as reference trajectories for air and goods temperatures. The PID parameters are $K_p=0.1, K_i=0.1, K_d=0.08$, selected through the use of a PID tuner in SIMULINK. The model was simulated for seven days (604,800 s). An output step disturbance with an initial value of zero and a final value of 4 was added to the output to depict the effect of door opening by the operator. The lower and upper bounds of the input constraints are valve (0 and 1), suction pressure (1.2 and 2 bar) and ambient temperature (9 and 30 °C). Due to the significant computational demand, the MATLAB-based Aquila optimization algorithm was created and simulated on a desktop computer with an Intel Core i7 (3.6 GHz) CPU and 8 GB of RAM. The tuned prediction and control horizon values, sampling time and weights of the linear MPC are: $N_p=70, N_u=2, T_s=5 \mathrm{secs}, Q\left(t\right)=diag\left(0.5,1.2,1.1\right) \mathrm{a}\mathrm{n}\mathrm{d} R\left(t\right)=diag\left(1,1\right).$

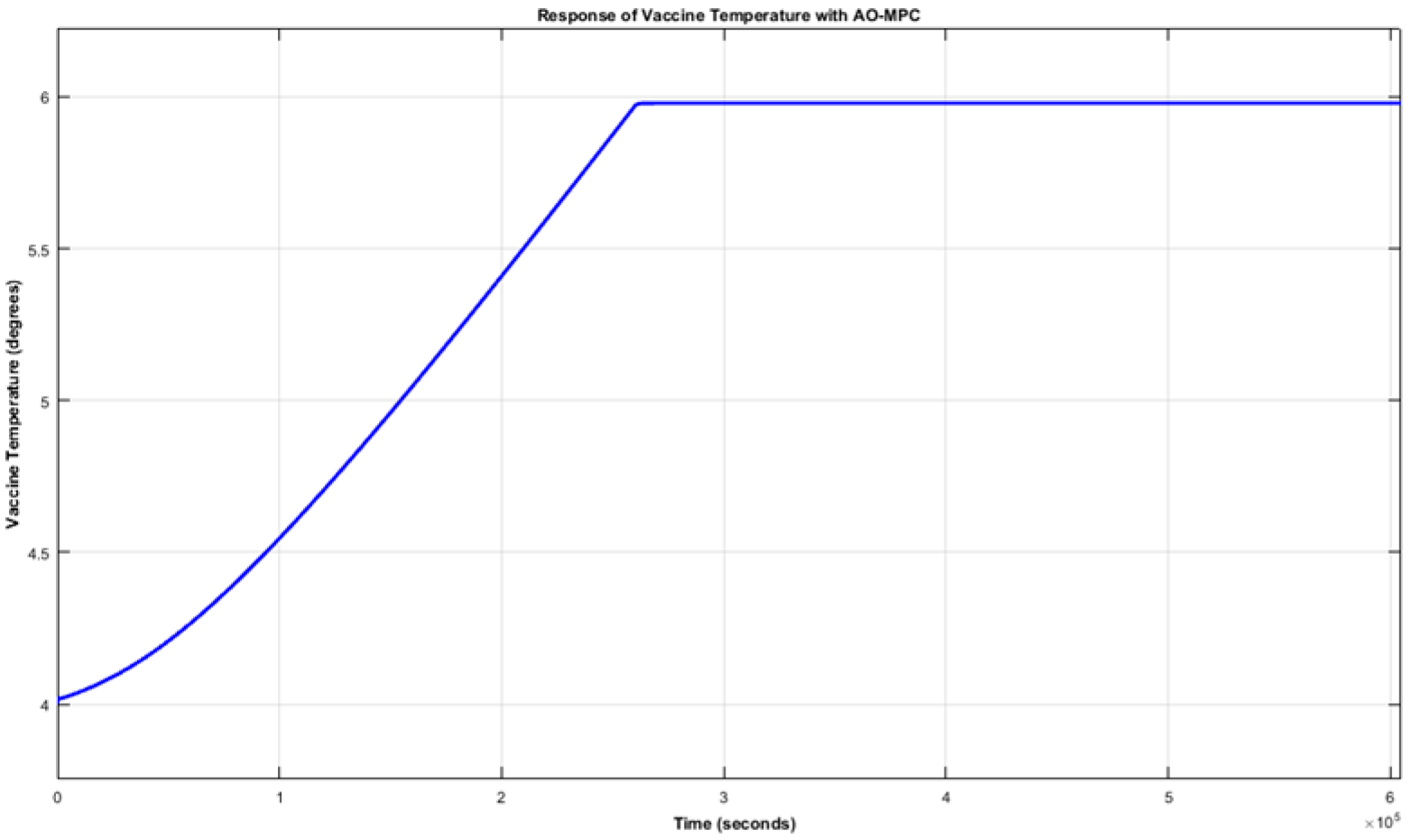
From Figure 1 and Figure 2, it can be observed that, by using AO-MPC, both the vaccine temperature and display case temperature settled at 5.98 °C, which is within the recommended temperature range for vaccine storage. This implies that the quality of any vaccine that will be kept in the refrigerated space will be maintained even in the presence of output disturbances such as the door opening of the refrigerator. This shows that AO-MPC is robust in accommodating bounded external disturbances.

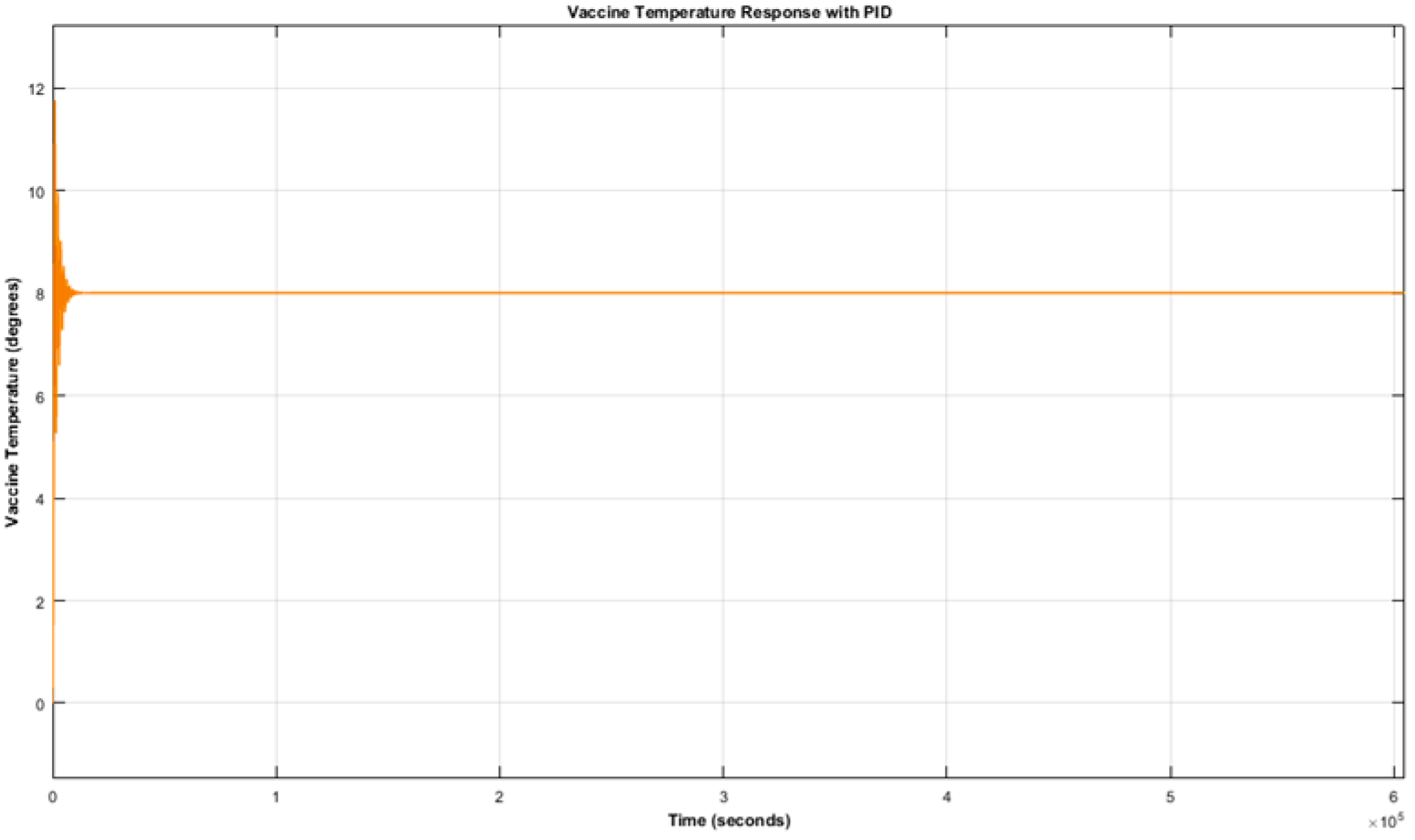
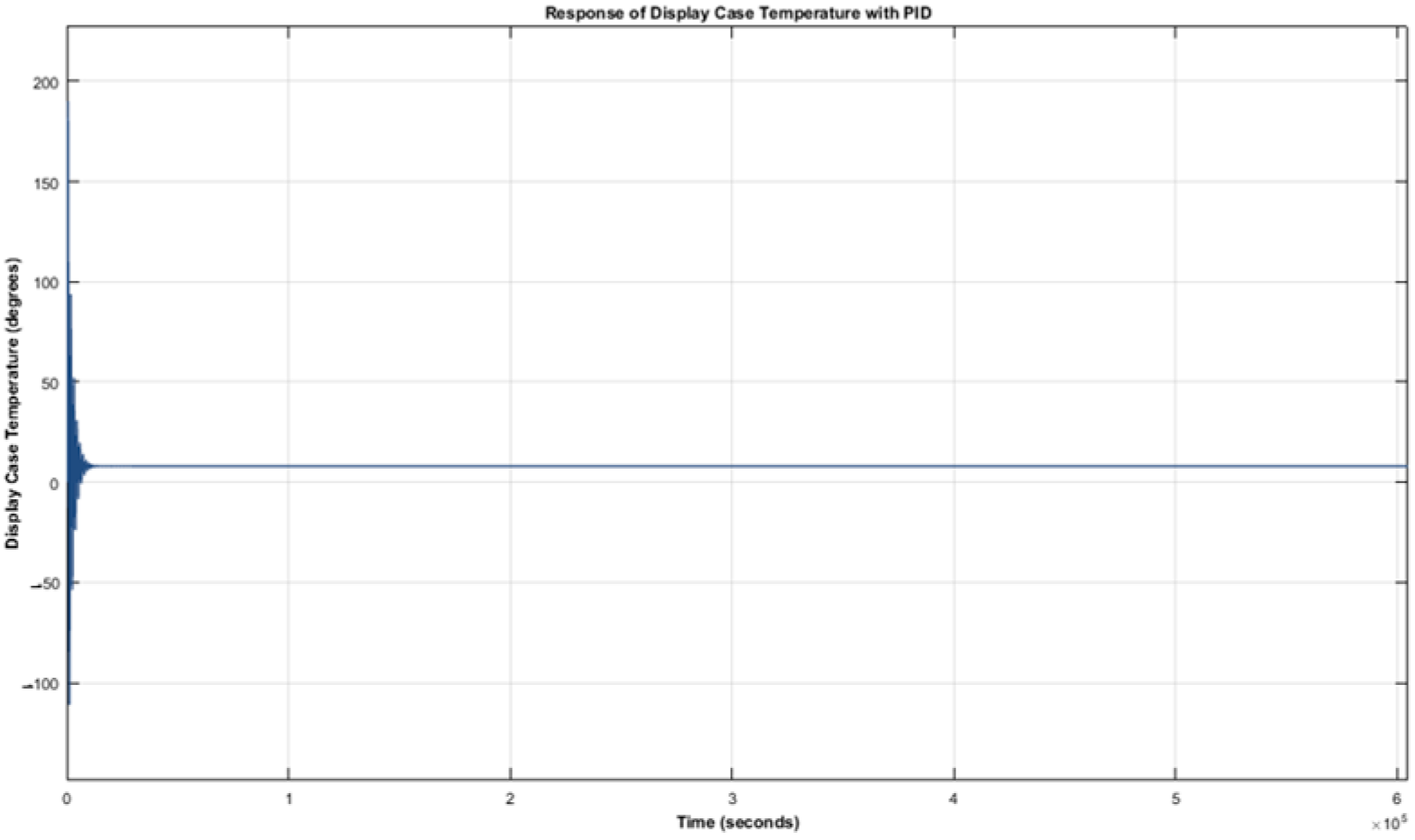
From Figure 3 and Figure 4, it can be observed that the vaccine and the display case temperature responses have initial oscillations for about 16,200 s (i.e., 4.5 h) before finally settling at 8 °C. This implies that temperature excursions occurred during the period of oscillation, making the stored vaccine temperature go beyond the recommended range, which is detrimental to vaccine potency. Therefore, it can be deduced that the PID controller is not suitable for the control of a fridge display case for the purpose of vaccine preservation.

4. Conclusions

A metaheuristic-based model predictive control strategy using Aquila optimizer for adapting a medium temperature fridge display case for vaccine preservation in primary health care centers of developing countries, where professional vaccine refrigerators are inadequate, is presented. The Aquila optimizer was able to stochastically determine the prediction and control horizon of the linear MPC by tuning. The use of AO-MPC was able to maintain the vaccine temperature within the recommended temperature range of 2 °C and 8 °C, as recommended by the drug authority, while the use of PID had initial oscillations above the recommended temperature range for about 4.5 h before finally settling at 8 °C. This shows that AO-MPC outperformed the PID controller in the presence of additive disturbances, such as the opening of the fridge display case, which could lead to infiltration of the heat load from the environment. The AO-MPC was found to be robust because it can accommodate external disturbances while maintaining the temperature constraints needed for vaccine safety and quality. This adaptation strategy will help to bridge the technical gaps in immunization programs in developing countries. Data-driven modelling and control will be the main topics of future research.