Abstract
This paper considers the problem of controlling a mobile robot in the presence of circular obstacles. To solve this problem, it is proposed to use the previously suggested principle of dividing permissible trajectories into a sequence of rectilinear sections and arcs of circles that are the boundaries of circular obstacles. The conditions for the solution based on this principle of optimality are obtained.
Suppose that the problem of controlling a mobile robot is solved using the principle of dividing feasible trajectories [1]. In the case of the phase space , this principle is an alternative to the classical optimal control theory based on the maximum principle [2]. According to this principle, a connected graph is first constructed, then the shortest path on the graph is searched. Taking into account that it is not the distance between the vertices that is used as the edges of the graph, but rather the minimum time rewuired for the robot to travel along the edge, we can assume that the time-optimal problem has been solved. However, this is true only under the essential condition that the robot, in bypassing a circular obstacle, always moves along the border of the obstacle, i.e., that the minimum allowable radius of curvature of the route is selected on the turn. Nevertheless, there is doubt that such a choice is always optimal in terms of performance. This is clearly seen in the example of auto racing, when, in seeking to overtake an opponent, the driver tries to avoid heavy braking on a curve, instead choosing a larger radius of curvature. If the driver chooses too high a speed at this point, slippage may occur, i.e., loss of grip with the surface of the track, resulting in displacement in the direction of the centrifugal force of inertia or even in the vehicle overturning.
On this basis, let us consider the main factors influencing the reasonable choice of the radius of curvature for the trajectory of the device when bypassing a circular obstacle. As already noted, an object moving along the arc of a circle is affected by the so-called centrifugal force of inertia F, which acts along the radius from the center of the circle and is calculated by the formula
where m is the mass of the object, is its angular speed, and r is the radius of the circle. This force is opposed by the force G of adhesion to the surface of the highway acting in the opposite direction, which is determined by weather conditions, the condition of the road surface, and the wheels of the car or robot.
Let us consider a concrete example (see Figure 1) in which a controlled device must move from point A to point B while bypassing a circular obstacle of radius (a circle of dark color) or an obstacle of radius (a circle of light color).
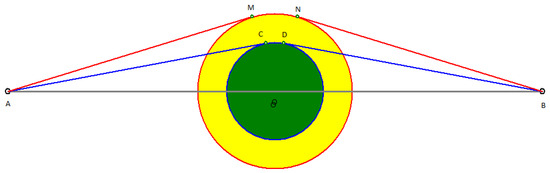
Figure 1.
Passage of a vmrage with a different radius.
For simplicity, assume that the distances from points A and B to the center of the circles are the same and are equal to S. The points C, D, M, and N are the tangent points of the lines drawn from A and B to the small and large circles. Let us define the conditions under which, from the point of view of time consumption, it is preferable to bypass a circular obstacle along an arc of a small radius or along an arc of a large one, provided that and
i.e., the passage of the turn is guaranteed against slippage.
Let . Note that the coefficient cannot be arbitrarily large, as at point A already falls inside the circle and the task loses its meaning. Due to the symmetry of the tracks in both cases with respect to a straight line passing through the center of the circles parallel to the ordinate axis, we estimate the time of passage of the left half of the trajectories. Let us first determine the time spent on moving along the arcs of circles. Suppose that the linear speed of motion along a small arc, corresponding to the fulfillment of the condition (3) at , is equal to and determines the feasible linear speed . It follows from (3) that , i.e., . As is well known, ; therefore,
It is easy to see that the angles based on the half-arcs of the circles are equal to and , respectively. Then, the lengths of the arcs themselves are and . Due to the uniform motion along these arcs with speeds and , we obtain expressions for time and . Thus,
as the expression in parentheses is obviously positive.
Now, let us estimate the time for the device to pass straight-line line break sections of the route to the points of contact C and M. Recall that, according to the assumptions, the robot starts moving at point A at a speed of , and should arrive at the touch point at a speed of . Let us first determine the time spent in both cases on braking, which we denote by . We have , i.e.,
meaning that in this case the distance traveled by the robot during braking is equal to . Thus, with the maximum speed , the robot travels the distance , with the time spent on this task being
Hence,
Thus, it follows from (4)–(6) that in both cases the difference in the time taken by the device to pass half of the trajectory is expressed by
Let us now evaluate the second term in this expression. Taking into account that for , and assuming that , we have
Therefore,
Let . Then, the last expression in (8) takes the form
moreover, the right side of this inequality takes a positive value when
Obviously, the estimate for the second half of the route takes the same form (9) with the replacement of by . Thus, the following statement is true.
Theorem 1.
Assume that the coupling force G and the maximum speed when passing a turn along the minimum allowable radius are known. Then, for any γ satisfying the inequality
where .
Thus, with a sufficient natural condition for the parameter , the solution of the time-optimal problem based on the principle of trajectory division is optimal. This is confirmed by computational experiments.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bereznev, V.A. The principle of dividing feasible trajectories in a robot control problem. Procedia Comput. Sci. 2021, 186, 456–459. [Google Scholar] [CrossRef]
- Pontryagin, L.; Boltyanskii, V.; Gamkrelidze, R.; Mishchenko, E.L. The Mathematical Theory of Optimal Processes; Publishing House: Interscience, NY, USA, 1962. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).