Abstract
This contribution investigates the performance of nature-inspired multi-objective optimization algorithms to reduce the makespan and oven idle time of bakery manufacturing using a hybrid no-wait flow shop scheduling model. As an example, the production data from a bakery with 40 products is investigated. We use the non-dominated sorting genetic algorithm (NSGA-II) and multi-objective particle swarm optimization (MOPSO) to determine the tradeoffs between the two objectives. The computational results reveal that the nature-inspired optimization algorithms provide solutions with a significant 8.7% reduction in makespan. Nonetheless, the algorithms provide solutions with a longer oven idle time to achieve the single goal of makespan minimization. This consequently elevates energy waste and production expenditure. The current study shows that an alternative Pareto optimal solution significantly reduces oven idle time while losing a marginal amount of makespan. Furthermore, the Pareto solution reduces oven idle time by 93 min by expanding the makespan by only 8 min. The proposed approach has the potential to be an influential tool for small- and medium-sized bakeries seeking economic growth and, as a result, gain in market competition.
1. Introduction
In a bakery production line, a product goes through a series of processing tasks, such as preparation, kneading, dividing, dough rest, shaping, proofing, and baking. Moreover, the total number, duration, and order of tasks are exclusive to the product recipes. Either a person or a machine performs each task until the final product is ready. The order of the processing stage is strictly followed for a product; each processing stage must be finished before moving on to the next. Furthermore, no time gap between two consecutive stages is permissible. Most of the time, multiple alternative machines of the same functionality run in parallel, and bakers select one that meets the product specification. To ensure the quality of final goods, these are fundamentals of the bakery manufacturing environment. Above all, one has to think that a machine or an employee can perform one task at a time.
As the number of products and processing stages grows, it becomes more difficult for a person to keep track of these conditions. The biggest challenges, however, are in optimizing the production schedule. In brief, scheduling is assigning tasks from products to machines. The distribution of tasks across the machines determines the efficiency of a manufacturing line. The main efficiency criterion, in reality, is makespan, which accounts for most of the manufacturing costs. The shorter the makespan, the more efficient the production, and to achieve this, tasks must be efficiently assigned to machines and employees.
Aside from makespan, energy consumption is another factor that determines the level of optimization of a manufacturing line. The duration and machine setup for tasks in the bakery are predetermined; they are not dependent on schedule. However, the idle time of machines depends on the distribution of the tasks. When a machine has two tasks with a wider gap between them, the amount of energy consumed during that time will be higher—a waste of energy. Therefore, the idle time of machines can be an ideal indicator of energy waste during bakery production.
In reality, most of the machines in bakeries are ready-to-use, which means they do not require any preparation time before performing an operation, such as a kneader, or a bread slicer. To avoid wasting energy, bakers turn them off after completing the task. In contrast, the baking oven requires preparation time to attain the predefined temperature. If an oven is turned off after performing one task, the temperature drops, requiring a re-start before starting the next baking task. If the preparation time is longer than expected, many tasks have to be postponed accordingly. In contrast, if the oven is preheated but has to wait longer for the products to finish the previous stage, it causes a waste of energy again. To ignore all these complexities and keep the workflow continuous, bakers simply keep the oven running throughout the production time. As a result, because a bakery has several ovens, this practice causes a waste of a significant quantity of energy. Consequently, the cost of production and CO2 emissions rise.
In the literature, such problems are known as flow shop scheduling problems, where optimization algorithms are used to find a cost-effective production schedule. Bakery manufacturing has received the least attention in terms of production optimization. Hecker et al. investigated a production line with 40 bakery products from a medium-size bakery in Germany. The study found that existing production was inefficient in terms of makespan. It recommended a better production schedule with an 8.6% reduction in makespan using particle swarm optimization and genetic algorithm [1]. Babor et al. observed a comparable result for a small Spanish bakery. The study revealed that the analyzed production line’s makespan can be reduced by 29%. It has been reported that a production schedule with the shortest possible makespan does not imply the shortest idle time. The authors observed that when oven idle time is factored into the optimization objective along with makespan reduction, it can be reduced by up to 8% [2].
In this paper, we investigated the same production data as Hecker et al. [1]. However, we conducted a comparative study between single objective and multi-objective optimization. In the case of single objective runs, we considered makespan as the objective and used genetic algorithm (GA) and particle swarm optimization (PSO) to minimize it. Furthermore, we extended it by using multi-objective optimization algorithms, NSGA-II and MOPSO. For multi-objective runs, besides makespan, we account the energy waste through oven idle time (OIDT) reduction to ensure that higher production efficiency is achieved.
2. Materials and Methods
According to Hecker et al., the investigated bakery had an unlimited capacity to perform dough rest and proofing. There were three different types of baking ovens, namely baking1, baking2, and baking3 with a capacity of 2, 6, and 1, respectively. The capacity value expresses the number of products that can be baked at a time. It is worth noting that the oven type for baking a product is predetermined. However, no particular information on the OIDT of the actual schedule is available. As a result, the OIDT of several optimal solutions will be evaluated in this study to obtain the most efficient solution to the problem. To study the dependence of OIDT on makespan, single objective optimizations were conducted with varied iteration sizes. However, multi-objective optimizations were performed only once to find the optimal solutions in the least amount of time. The following subsections describe the problem and optimization algorithms.
2.1. Problem Description
Table 1 shows the tasks and associated duration for two simplified product recipes. In reality, the number of products and their stages is higher. A machine in a production setting can only accomplish one task at a time. However, there is no such restriction for dough rest and proofing, therefore these tasks from several products can be performed at the same time. There are two different production schedules for two items, depending on the order of the products when they are produced: (Product A, Product B) and (Product B, Product A). Figure 1 presents the schedule using the former option where makespan and oven idle time are 220 min and 17 min, respectively. However, for the latter choice, they are 240 min and 0 min, respectively. The former option provided a schedule with a minimum makespan while having higher OIDT and the second option increased the makespan by 20 min and reduced OIDT to 0 min. The options demonstrate a tradeoff between makespan and OIDT, which can be substantial in real-world scenarios with a large number of products.

Table 1.
Simplified production data for two products.

Figure 1.
The schedule of the products that are shown in Table 1 with a production order of {Product A, Product B} where ∆ shows the oven idle time.
In principle, an unfinished product must wait until a machine is available. In contrast, the delay between two successive stages is undesirable in a bakery. Instead, a product begins later to ensure that a machine is available at the beginning of each stage. In the schedule shown in Figure 1, product B starts 15 min later to ensure that kneading is performed on time. This raises the makespan and perhaps also the OIDT. Therefore, it is critical to find the order of product in the production, so that the makespan and OIDT are both optimized. However, for 40 products, there are 40 or distinct schedules. Finding optimal schedules with a minimum makespan and OIDT is a challenging task. To find the best tradeoffs between the objectives, a multi-objective optimizer is used.
2.2. Multi-Objective Optimization Algorithms
A multi-objective optimization problem has more than one criterion or objective, satisfying one of which leaves the others unsatisfied. Instead of a single optimal solution, a set of optimal solutions is derived in this scenario. They are called Pareto optimal solutions that show the tradeoffs between objectives in a decision space. During runtime, an optimization algorithm produces many solutions, most of which are not optimal. The evaluation approach for a single objective is simple: one value is compared to another. With multi-objectives, however, the evaluation technique must consider each objective in order to determine whether or not a solution is optimal. The Pareto dominance is a basic operator in multi-objective optimization, which is often employed to address this problem. Let us assume that are two solution vectors containing the objective values from different objectives. The index of the objectives can be defined with where . The solution is said to dominate , if is not worse in any objective and better in at least one objective (). Solution can be regarded as a Pareto optimum solution over if it meets these criteria.
2.2.1. Multi-Objective Particle Swarm Optimization (MOPSO)
The following is the multi-objective particle swarm optimization (MOPSO) algorithm proposed by Coello et al. [3].
- Initialize the population with random particle positions. Initialize the speed of each particle in the population. Evaluate each particle to find the objective values.
- In a repository, save the positions of particles that are Pareto non-dominated in objective space.
- Generate hypercubes of the search space. These hypercubes act as a particle’s coordination system. The placement of a particle in this coordinate system is determined by its objective values.
- Initialize the memory of the best individual position that guides their movement.
- Calculate the velocity of each particle using Equation (1).
- Update the position of the particle using Equation (2).
The velocity is multiplied by −1 or set to the boundary if the particles move beyond the boundary.
- Evaluate each particle based on its updated position.
- Update the memory of the particles’ individual best positions if the new positions are better in terms of objective values than the previous best positions. Similarly, update the repository of non-dominated particles. Initially, the repository’s older members are combined with newly updated particles. The non-dominant particles are then archived in the repository.
- Repeat steps 5–8 until the termination criterion, such as the number of iterations, is reached.
2.2.2. Non-Dominated Sorting Genetic Algorithm II (NSGA-II)
The NSGA-II algorithm was first proposed by Deb et al. [4]. The following is a brief description of the algorithm.
- Initialize the random population of size with each individual representing a schedule.
- Assess the individuals in order to determine objective values. Sort the individuals into distinct rankings based on objective values using the fast non-dominated sorting approach (Deb et al., 2002), which is discussed later.
- The crossover and mutation operators are used to establish a new offspring population of size. Each time, two parents are chosen for this course. A binary tournament is used to find each parent, in which four individuals from the current population are picked at random and the one with the best rank is selected.
- Use the fast non-dominated sorting strategy for the combined population of size from parents and offspring to sort into different ranks.
- Because the present population has doubled, apply a screening technique to keep only the best individuals. Individuals with the best ranking are chosen to fill the vacant slots in the best population. If the slots are still empty, use the subsequent ranks. However, if any subsequent rank contains more individuals than the empty slot in the best population, use the crowding distance operator. The individuals are sorted in descending order of crowding distance. Individuals with a higher crowding distance fill the empty slots first until the best population size reaches . Set the crowding distance for border individuals to infinity, guaranteeing that they are prioritized in the selection process.
- Employ crossover and mutation to produce offspring from the best population.
- Repeat steps 4–6 until the termination criterion is reached.
In the fast non-dominated sorting approach, the fitness of each individual is compared with that of other individuals. Let us assume a set of individuals in the population. If the fitness of is compared with , the Pareto dominance operator provides one of three following outcomes: dominates , dominates or no-one dominates none.
The number of other individuals that dominate determines its rank. The rank can be defined with where . If is dominated by none of the other individuals, implying the sum of domination is 0 and thus the rank of can be declared as . In other words, the rank contains all non-dominated solutions and forms a Pareto frontier. The sum of domination for the members of a rank is the same. Therefore, each rank produces an independent frontier. However, individuals in are suboptimal compared to that of [4].
3. Results and Discussion
Initially, the goal was to reduce only makespan, which was found to be the same, 1259 min for different iteration sizes of PSO and GA. When compared to the actual production line efficiency, these schedules reduce the makespan by 8.7%. However, the OIDT for these optimized schedules displayed no pattern and appeared to be dispersed unevenly between 139 min and 368 min. It raises the possibility of significant waste in terms of cost and CO2 emissions that may be avoided from an operational perspective. Figure 2 shows the OIDT distribution is derived by PSO and GA with various iteration sizes. This suggests that having the shortest makespan does not guarantee the shortest OIDT.
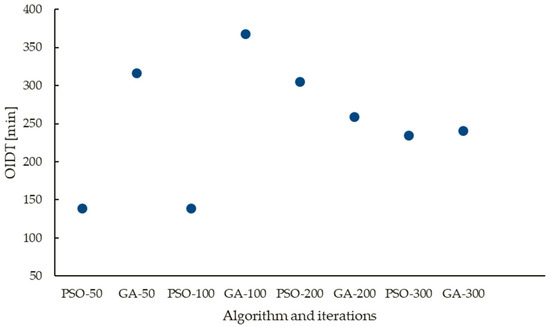
Figure 2.
The oven idle time (OIDT) of the schedules with the same makespan of 1259 min. The schedules were found by PSO and GA with an objective to minimize the makespan. PSO-50 indicates one run of PSO with 50 iterations.
Furthermore, if only the makespan is counted in optimization, there is a high chance that a significant amount of energy will be wasted due to the long oven idle time.
In contrast, multi-objective optimization generates a collection of several Pareto optimal solutions by considering both makespan and OIDT. Figure 3 shows the optimal solutions obtained by NSGA-II and MOPSO. Each method generated a unique front, but none of them could create the complete Pareto front (PF) for the problem.

Figure 3.
Set of optimal solutions provided by MOPSO and NSGA-II with 50 iterations. The combined Pareto solutions from the algorithms are indicated by S1, …, S11.
The PF displays 11 solutions with a makespan increase of 43 min and an OIDT reduction of 133 min over the front. It means that a marginal increase in the makespan can result in a substantial decrease in OIDT (by up to 80%). However, the rate of gain is not the same for all the Pareto solutions. PF shows that despite increasing the makespan, the drop in OIDT after S6 is not significant. It can be verified by calculating the conversion rate (CR) from makespan to OIDT at every Pareto solution. The CR denotes the decrease in OIDT caused by a 1% increase in makespan over the best makespan determined at solution S1. Compared to S1, solution S6 gives a CR of 89. In other words, because all PF solutions are Pareto optimal, the bakery manufacturing line can follow these schedules. However, if the solution S6 is adopted instead of S1 with the shortest makespan, OIDT can be reduced by 93 min while giving up only 8 min of makespan. The result can be improved if the optimization is performed many times, or the iteration size is increased.
4. Conclusions
The manufacturing efficiency of most small and medium-sized bakeries is under-optimized. Aside from makespan, energy consumption by ovens drives up manufacturing costs substantially. Indirect metrics, such as oven idle time, can compensate for the difficulty in collecting data on energy consumption. Using multi-objective optimization algorithms, the study revealed that both the makespan and the oven idle time were minimized at the same time. The set of Pareto-optimal solutions added to the possibilities for finding a reasonable tradeoff between makespan and oven idle time that results in cost-effective manufacturing and lowers CO2 emissions.
Author Contributions
Conceptualization, M.B.; methodology, M.B.; software, M.B.; formal analysis, M.B.; data curation, M.B.; writing—original draft preparation, M.B.; supervision, B.H.; project administration, B.H.; funding acquisition, B.H. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by EIT Food of the European Institute of Innovation and Technology (EIT), a body of the European Union, the E.U. Framework Program for Research and Innovation for the project entitled “Optimization of bakery processes by a computational tool together with consumer feedback to minimize ecological footprint and food waste: Making baking more efficient”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
For this study, production data from a bakery in Germany was used. It was taken from Hecker et al. [1].
Conflicts of Interest
The authors confirm having no known involvement in any organization with any financial interest in the subject and materials presented in this manuscript.
References
- Hecker, F.T.; Stanke, M.; Becker, T.; Hitzmann, B. Application of a modified GA, ACO and a random search procedure to solve the production scheduling of a case study bakery. Expert Syst. Appl. 2014, 41, 5882–5891. [Google Scholar] [CrossRef]
- Babor, M.; Senge, J.; Rosell, C.M.; Rodrigo, D.; Hitzmann, B. Optimization of No-Wait Flowshop Scheduling Problem in Bakery Production with Modified PSO, NEH and SA. Processes 2021, 9, 2044. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Toscano-Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).