Multi-Layer Perceptron Neural Networks for Concrete Strength Prediction: Balancing Performance and Optimizing Mix Designs †
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Dataset
2.2. Methodology
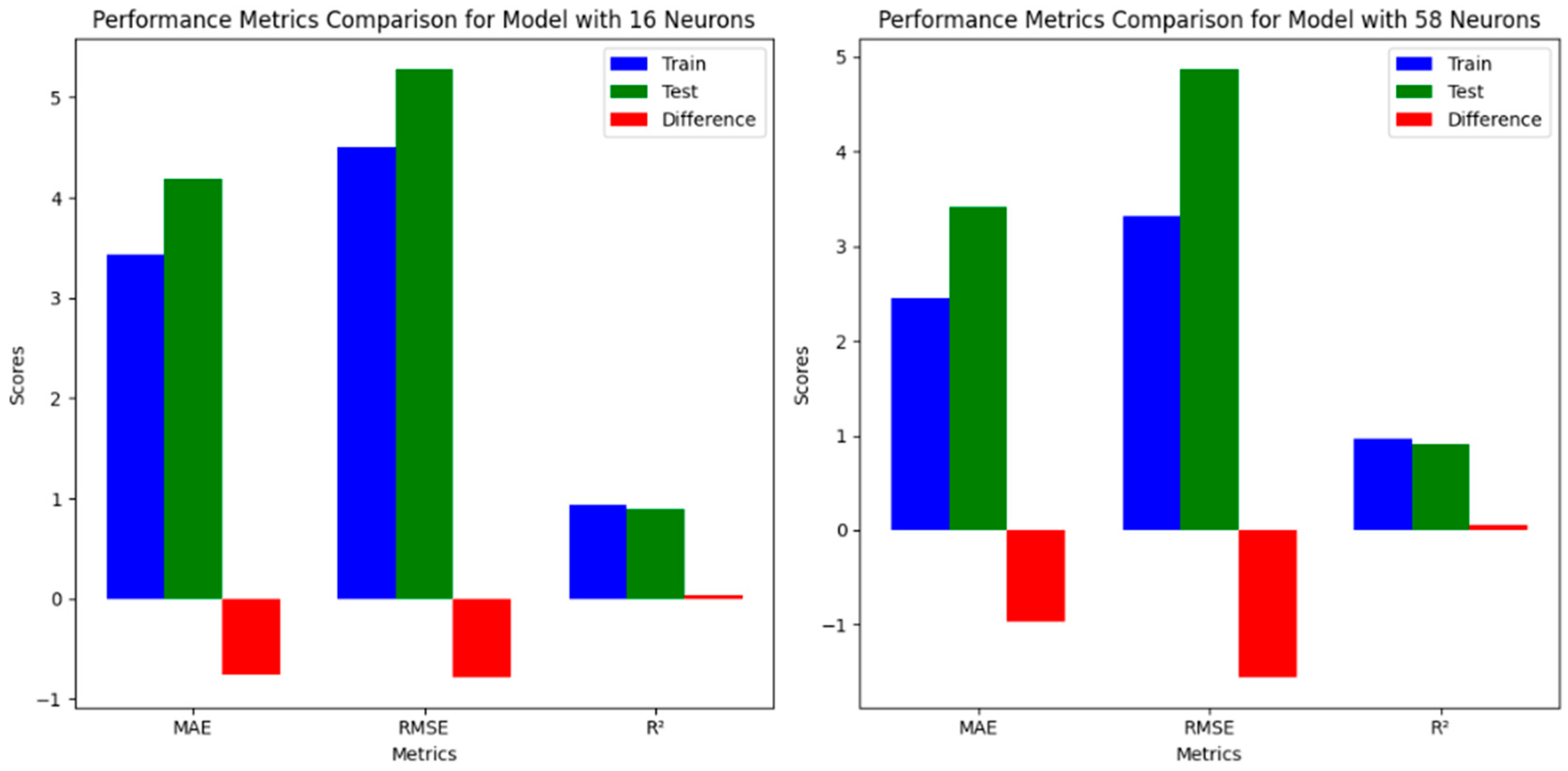
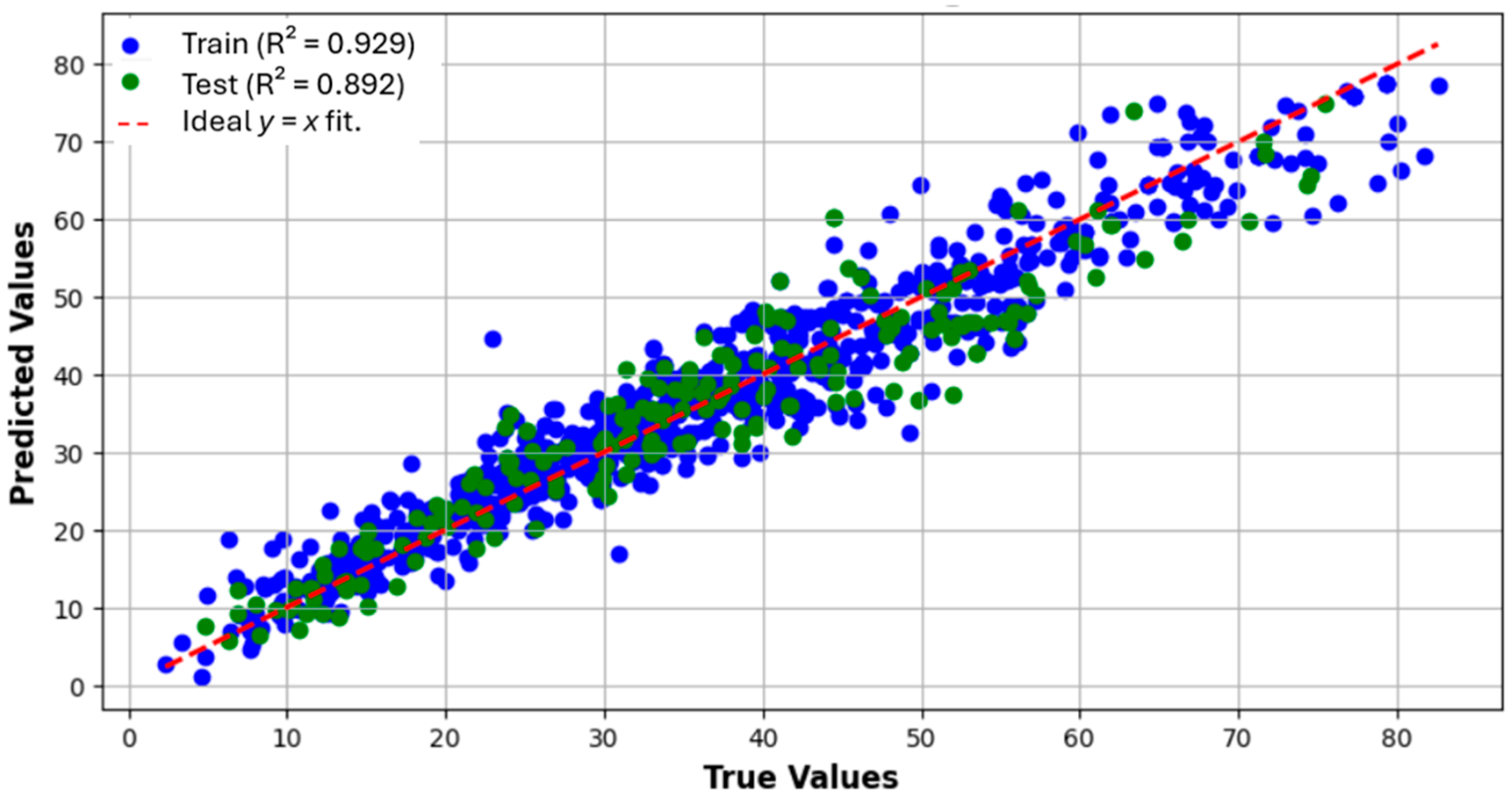
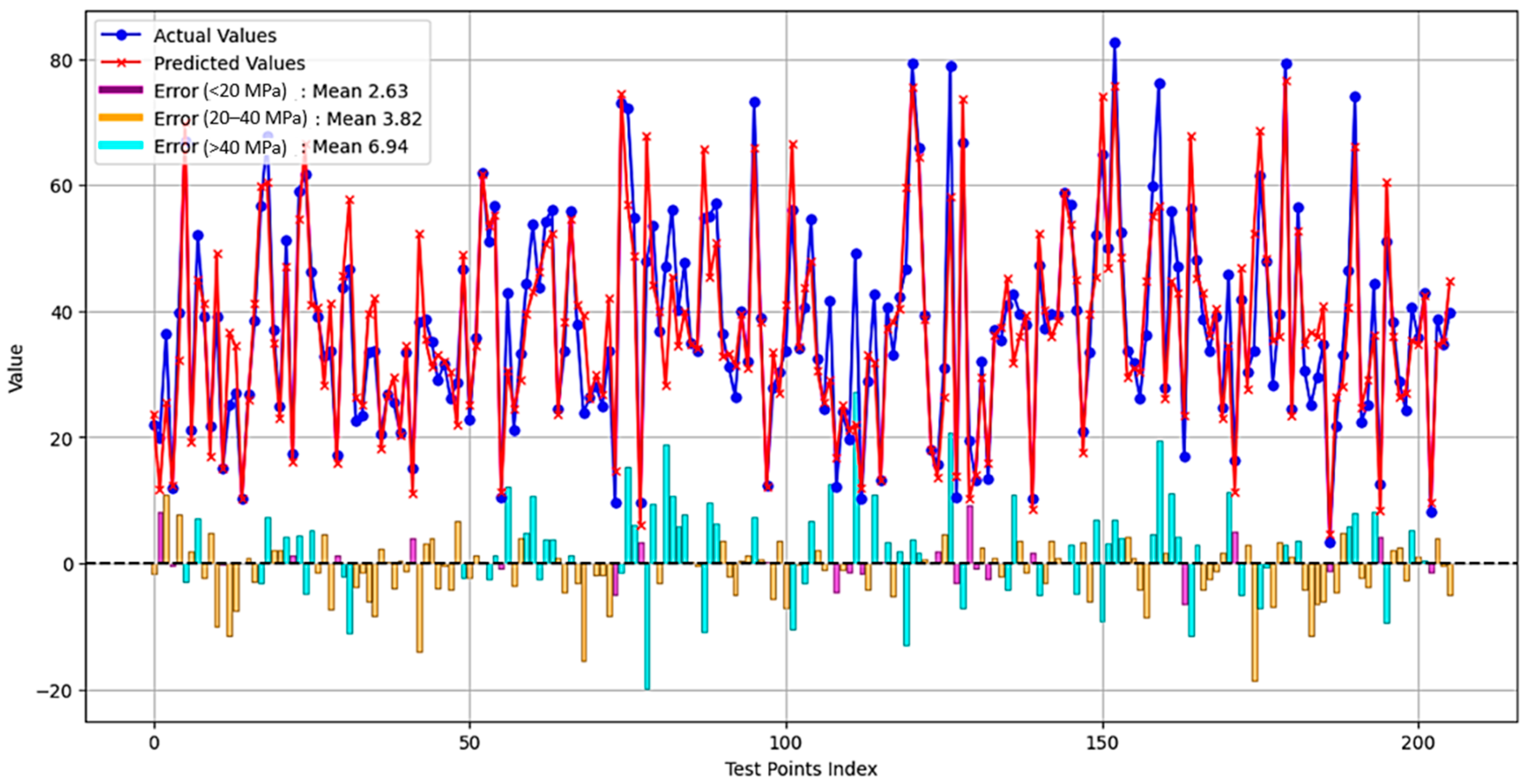
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ben Chaabene, W.; Flah, M.; Nehdi, M.L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 2020, 260, 119889. [Google Scholar] [CrossRef]
- Moein, M.M.; Saradar, A.; Rahmati, K.; Mousavinejad, S.H.G.; Bristow, J.; Aramali, V.; Karakouzian, M. Predictive models for concrete properties using machine learning and deep learning approaches: A review. J. Build. Eng. 2023, 63, 105444. [Google Scholar] [CrossRef]
- Gamil, Y. Machine learning in concrete technology: A review of current researches, trends, and applications. Front. Built Environ. 2023, 9, 1145591. [Google Scholar] [CrossRef]
- Ziolkowski, P.; Niedostatkiewicz, M. Machine Learning Techniques in Concrete Mix Design. Materials 2019, 12, 1256. [Google Scholar] [CrossRef] [PubMed]
- Azimi-Pour, M.; Eskandari-Naddaf, H.; Pakzad, A. Linear and non-linear SVM prediction for fresh properties and compressive strength of high volume fly ash self-compacting concrete. Constr. Build. Mater. 2020, 230, 117021. [Google Scholar] [CrossRef]
- Sonebi, M.; Cevik, A.; Grünewald, S.; Walraven, J. Modelling the fresh properties of self-compacting concrete using support vector machine approach. Constr. Build. Mater. 2016, 106, 55–64. [Google Scholar] [CrossRef]
- Sobuz, H.R.; Imran, A.; Datta, S.D.; Jabin, J.A.; Aditto, F.S.; Hasan, N.M.S.; Hasan, M.; Zaman, A.A.U. Assessing the influence of sugarcane bagasse ash for the production of eco-friendly concrete: Experimental and machine learning approaches. Case Stud. Constr. Mater. 2024, 20, e02839. [Google Scholar] [CrossRef]
- Hasan, N.M.S.; Sobuz, H.R.; Shaurdho, N.M.N.; Meraz, M.; Datta, S.D.; Aditto, F.S.; Kabbo, K.I.; Miah, J. Eco-friendly concrete incorporating palm oil fuel ash: Fresh and mechanical properties with machine learning prediction, and sustainability assessment. Heliyon 2023, 9, e22296. [Google Scholar] [CrossRef]
- Nadimalla, A.; Masjuki, S.; Saad, S.; Ali, M. Machine Learning Model to Predict Slump, VEBE and Compaction Factor of M Sand and Shredded Pet Bottles Concrete. IOP Conf. Ser. Mater. Sci. Eng. 2022, 1244, 012023. [Google Scholar] [CrossRef]
- Öztaş, A.; Pala, M.; Özbay, E.; Kanca, E.; Çaǧlar, N.; Bhatti, M.A. Predicting the compressive strength and slump of high strength concrete using neural network. Constr. Build. Mater. 2006, 20, 769–775. [Google Scholar] [CrossRef]
- Yan, K.; Shi, C. Prediction of elastic modulus of normal and high strength concrete by support vector machine. Constr. Build. Mater. 2010, 24, 1479–1485. [Google Scholar] [CrossRef]
- Bui, D.-K.; Nguyen, T.; Chou, J.-S.; Nguyen-Xuan, H.; Ngo, T.D. A modified firefly algorithm-artificial neural network expert system for predicting compressive and tensile strength of high-performance concrete. Constr. Build. Mater. 2018, 180, 320–333. [Google Scholar] [CrossRef]
- Bashir, R.; Ashour, A. Neural network modelling for shear strength of concrete members reinforced with FRP bars. Compos. Part B Eng. 2012, 43, 3198–3207. [Google Scholar] [CrossRef]
- Nithurshan, M.; Elakneswaran, Y. A systematic review and assessment of concrete strength prediction models. Case Stud. Constr. Mater. 2023, 18, e01830. [Google Scholar] [CrossRef]
- Hamza, C.; Bouchra, S.; Mostapha, B.; Mohamed, B. Formulation of ordinary concrete using the Dreux-Gorisse method. Procedia Struct. Integr. 2020, 28, 430–439. [Google Scholar] [CrossRef]
- Hattani, F.; Menu, B.; Allaoui, D.; Mouflih, M.; Zanzoun, H.; Hannache, H.; Manoun, B. Evaluating the Impact of Material Selections, Mixing Techniques, and On-site Practices on Performance of Concrete Mixtures. Civ. Eng. J. 2024, 10, 571–598. [Google Scholar] [CrossRef]
- Kovler, K.; Roussel, N. Properties of fresh and hardened concrete. Cem. Concr. Res. 2011, 41, 775–792. [Google Scholar] [CrossRef]
- Ivanchev, I. Investigation with Non-Destructive and Destructive Methods for Assessment of Concrete Compressive Strength. Appl. Sci. 2022, 12, 12172. [Google Scholar] [CrossRef]
- Chou, J.-S.; Tsai, C.-F.; Pham, A.-D.; Lu, Y.-H. Machine learning in concrete strength simulations: Multi-nation data analytics. Constr. Build. Mater. 2014, 73, 771–780. [Google Scholar] [CrossRef]
- Abuodeh, O.R.; Abdalla, J.A.; Hawileh, R.A. Assessment of compressive strength of Ultra-high Performance Concrete using deep machine learning techniques. Appl. Soft Comput. 2020, 95, 106552. [Google Scholar] [CrossRef]
- Yeh, I.-C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Choudhary, L.; Sahu, V.; Dongre, A.; Garg, A. Prediction of compressive strength of sustainable concrete using machine learning tools. Comput. Concr. 2024, 33, 137–145. [Google Scholar] [CrossRef]
- Kumar, A.; Arora, H.C.; Kapoor, N.R.; Mohammed, M.A.; Kumar, K.; Majumdar, A.; Thinnukool, O. Compressive Strength Prediction of Lightweight Concrete: Machine Learning Models. Sustainability 2022, 14, 2404. [Google Scholar] [CrossRef]
- Khan, A.Q.; Awan, H.A.; Rasul, M.; Siddiqi, Z.A.; Pimanmas, A. Optimized artificial neural network model for accurate prediction of compressive strength of normal and high strength concrete. Clean. Mater. 2023, 10, 100211. [Google Scholar] [CrossRef]
- Feng, D.-C.; Liu, Z.-T.; Wang, X.-D.; Chen, Y.; Chang, J.-Q.; Wei, D.-F.; Jiang, Z.-M. Machine learning-based compressive strength prediction for concrete: An adaptive boosting approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Sah, A.K.; Hong, Y.-M. Performance Comparison of Machine Learning Models for Concrete Compressive Strength Prediction. Materials 2024, 17, 2075. [Google Scholar] [CrossRef] [PubMed]
- Al-Shamiri, A.K.; Kim, J.H.; Yuan, T.-F.; Yoon, Y.S. Modeling the compressive strength of high-strength concrete: An extreme learning approach. Constr. Build. Mater. 2019, 208, 204–219. [Google Scholar] [CrossRef]
- Deshpande, N.; Londhe, S.; Kulkarni, S. Modeling compressive strength of recycled aggregate concrete by Artificial Neural Network, Model Tree and Non-linear Regression. Int. J. Sustain. Built Environ. 2014, 3, 187–198. [Google Scholar] [CrossRef]
- Ni, H.-G.; Wang, J.-Z. Prediction of compressive strength of concrete by neural networks. Cem. Concr. Res. 2000, 30, 1245–1250. [Google Scholar] [CrossRef]
- Prasad, B.R.; Eskandari, H.; Reddy, B.V. Prediction of compressive strength of SCC and HPC with high volume fly ash using ANN. Constr. Build. Mater. 2009, 23, 117–128. [Google Scholar] [CrossRef]
- Topçu, I.B.; Sarıdemir, M. Prediction of properties of waste AAC aggregate concrete using artificial neural network. Comput. Mater. Sci. 2007, 41, 117–125. [Google Scholar] [CrossRef]
- Akbari, M.; Deligani, V.J. Data driven models for compressive strength prediction of concrete at high temperatures. Front. Struct. Civ. Eng. 2020, 14, 311–321. [Google Scholar] [CrossRef]
- Asteris, P.G.; Skentou, A.D.; Bardhan, A.; Samui, P.; Pilakoutas, K. Predicting concrete compressive strength using hybrid ensembling of surrogate machine learning models. Cem. Concr. Res. 2021, 145, 106449. [Google Scholar] [CrossRef]
- Shah, S.A.R.; Azab, M.; ElDin, H.M.S.; Barakat, O.; Anwar, M.K.; Bashir, Y. Predicting Compressive Strength of Blast Furnace Slag and Fly Ash Based Sustainable Concrete Using Machine Learning Techniques: An Application of Advanced Decision-Making Approaches. Buildings 2022, 12, 914. [Google Scholar] [CrossRef]
- Song, H.; Ahmad, A.; Farooq, F.; Ostrowski, K.A.; Maślak, M.; Czarnecki, S.; Aslam, F. Predicting the compressive strength of concrete with fly ash admixture using machine learning algorithms. Constr. Build. Mater. 2021, 308, 125021. [Google Scholar] [CrossRef]
- Wang, G.; Giannakis, G.B.; Chen, J. Learning ReLU Networks on Linearly Separable Data: Algorithm, Optimality, and Generalization. IEEE Trans. Signal Process. 2019, 67, 2357–2370. [Google Scholar] [CrossRef]
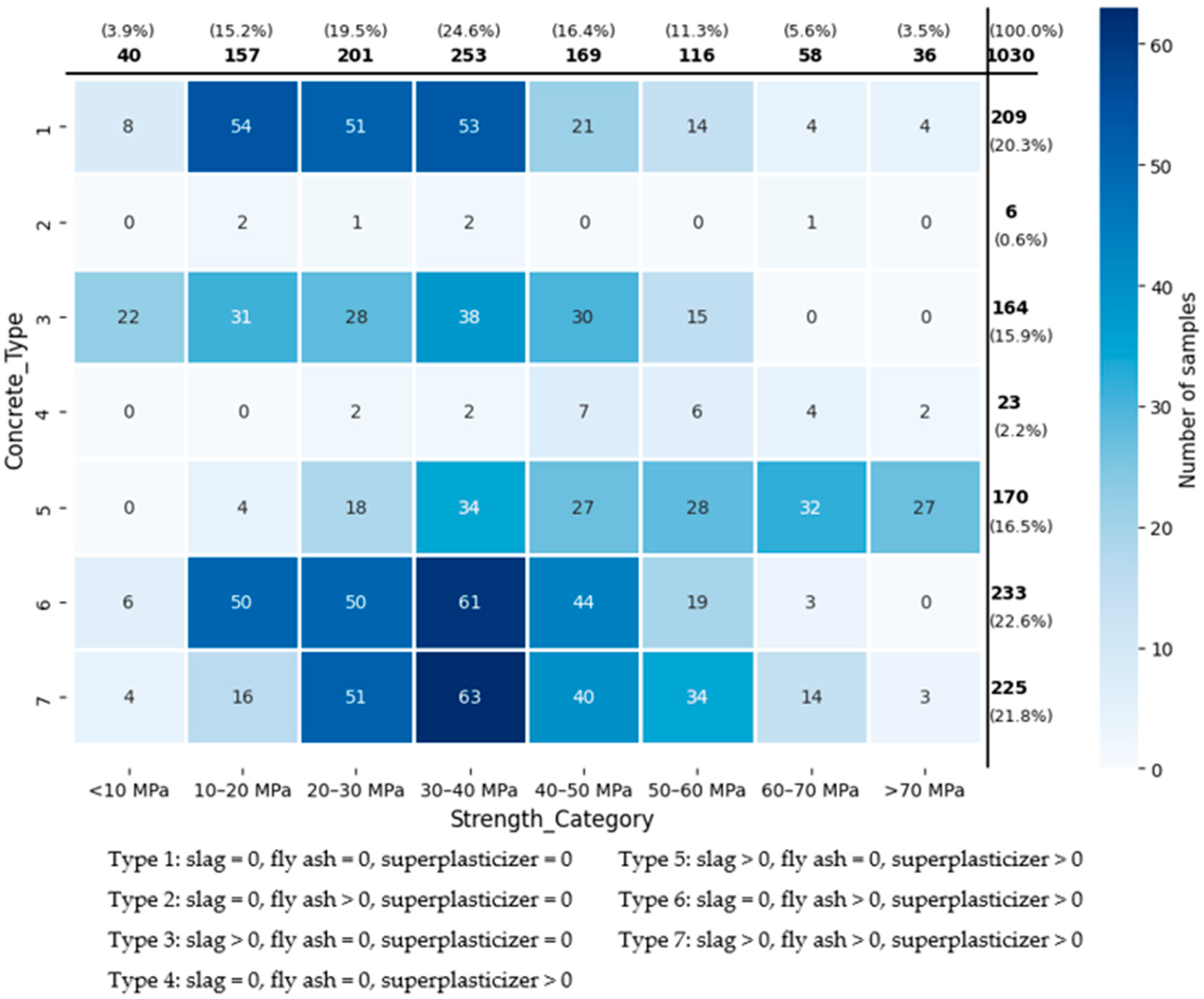

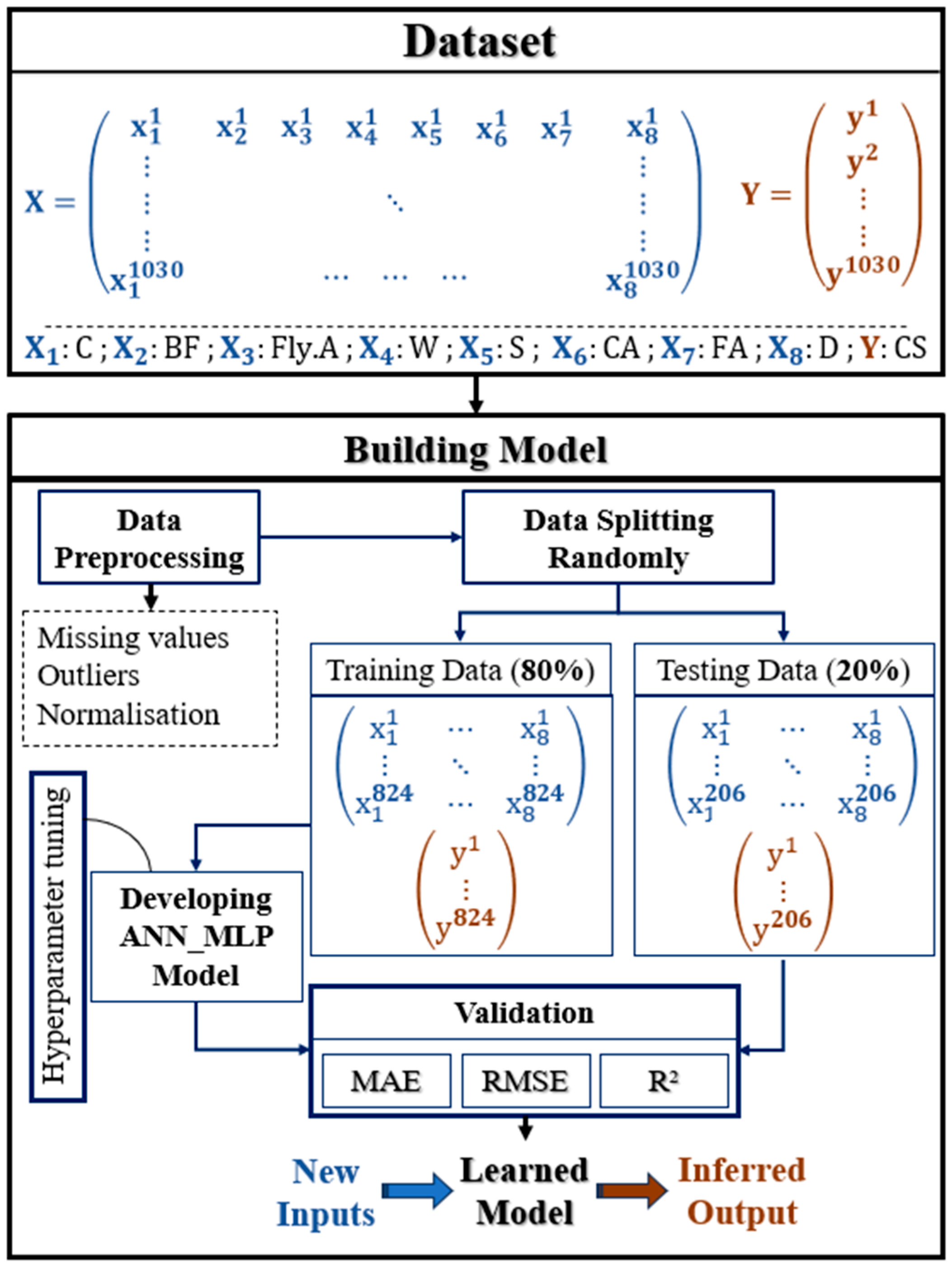
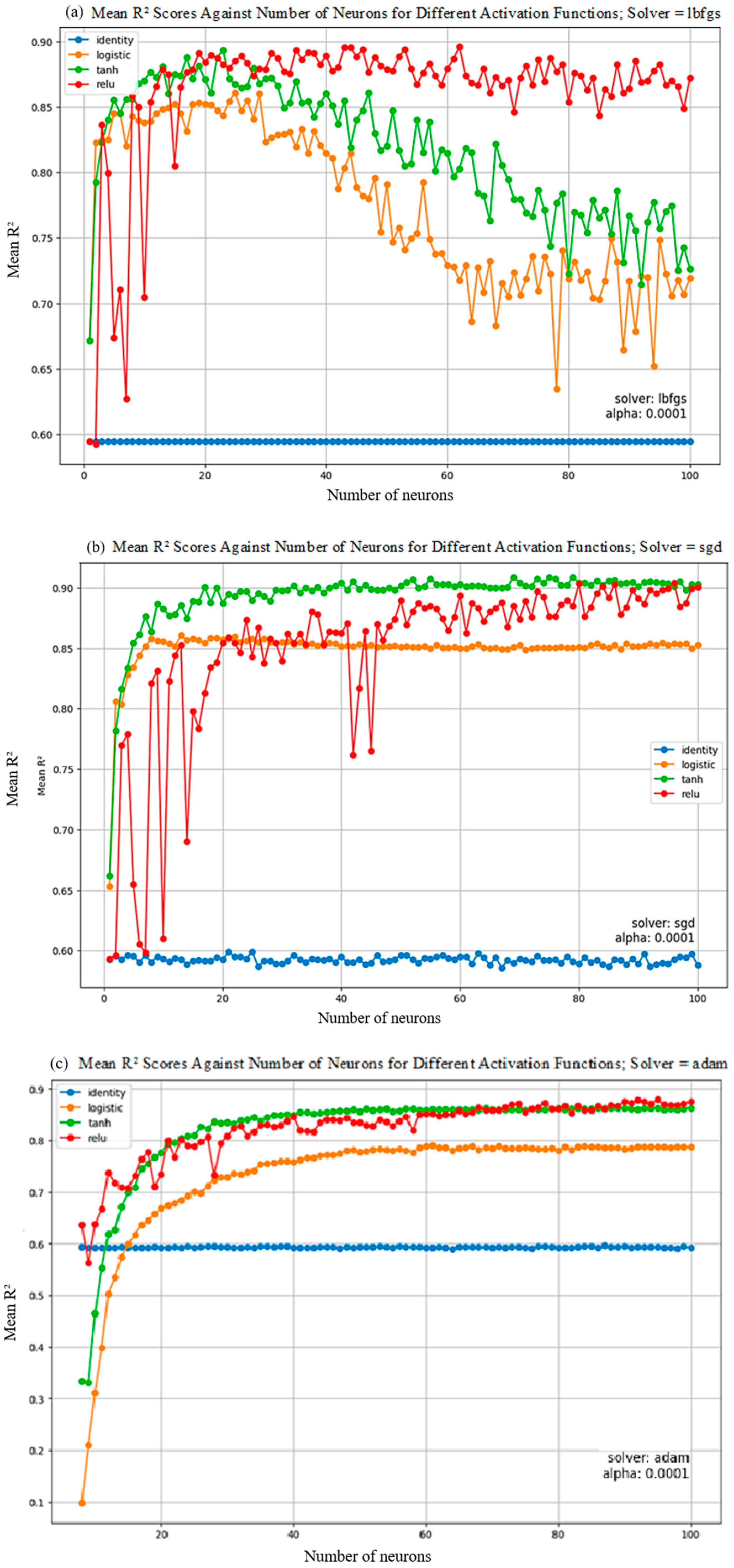
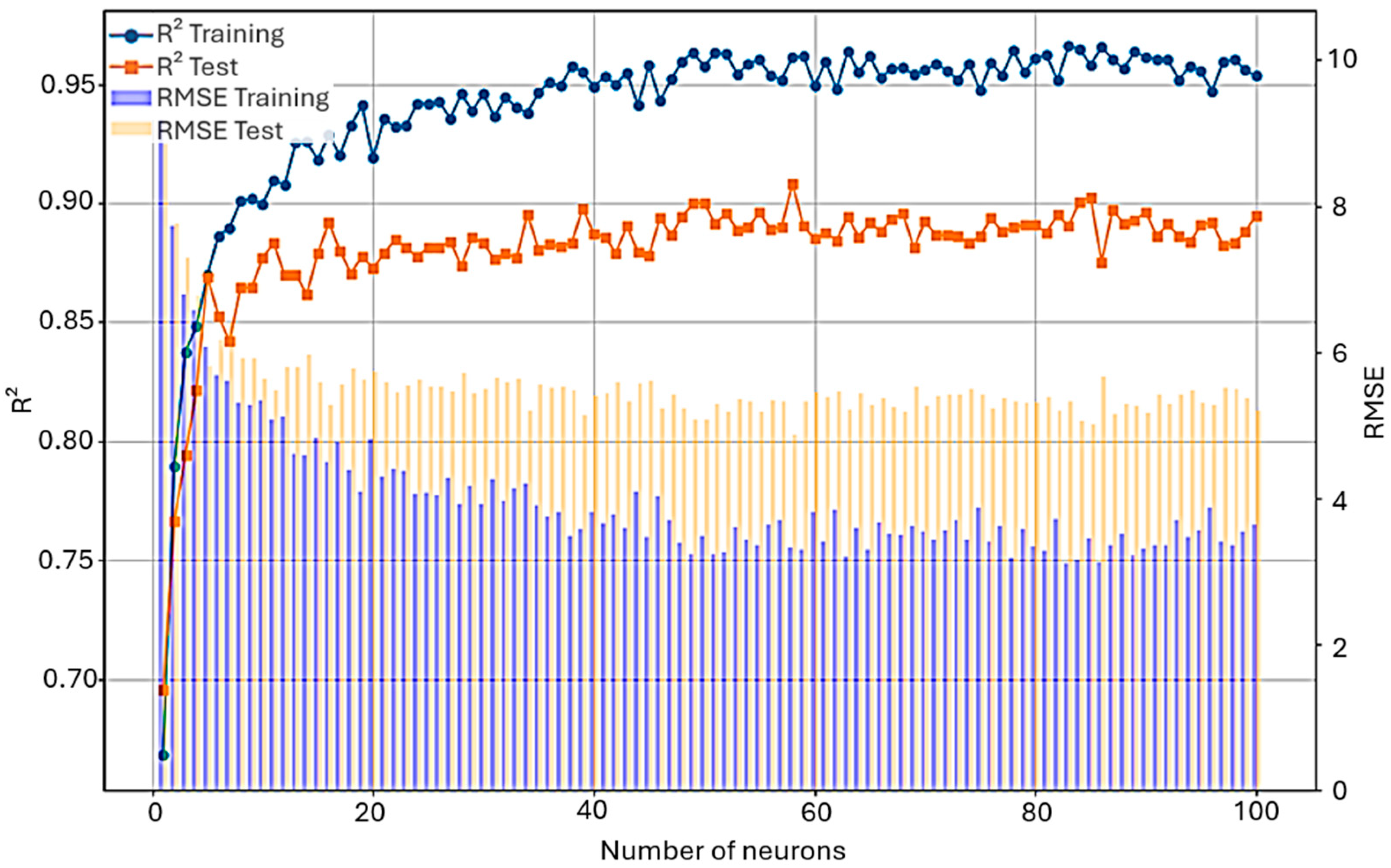
| Variable | Sym | Unit | Category | Mean | Min | Max | Std |
|---|---|---|---|---|---|---|---|
| Cement | C | Kg/m3 | Input | 281.2 | 102.0 | 540.0 | 104.5 |
| Blast Furnace Slag | BF | Kg/m3 | Input | 73.9 | 0.0 | 359.4 | 86.3 |
| Fly Ash | Fly.A | Kg/m3 | Input | 54.2 | 0.0 | 200.1 | 64.0 |
| Water | W | Kg/m3 | Input | 181.6 | 121.7 | 247.0 | 21.3 |
| Superplasticizer | S | Kg/m3 | Input | 6.2 | 0.0 | 32.2 | 6.0 |
| Coarse Aggregate | CA | Kg/m3 | Input | 972.9 | 801.0 | 1145.0 | 77.7 |
| Fine Aggregate | FA | Kg/m3 | Input | 773.6 | 594.0 | 992.6 | 80.2 |
| Age | D | Day | Input | 45.7 | 1.0 | 365.0 | 63.2 |
| Compressive Strength | CS | MPa | Output | 35.8 | 2.3 | 82.6 | 16.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alouan, Y.; Cherif, S.-E.; Kchakech, B.; Cherradi, Y.; Kchikach, A. Multi-Layer Perceptron Neural Networks for Concrete Strength Prediction: Balancing Performance and Optimizing Mix Designs. Eng. Proc. 2025, 112, 1. https://doi.org/10.3390/engproc2025112001
Alouan Y, Cherif S-E, Kchakech B, Cherradi Y, Kchikach A. Multi-Layer Perceptron Neural Networks for Concrete Strength Prediction: Balancing Performance and Optimizing Mix Designs. Engineering Proceedings. 2025; 112(1):1. https://doi.org/10.3390/engproc2025112001
Chicago/Turabian StyleAlouan, Younes, Seif-Eddine Cherif, Badreddine Kchakech, Youssef Cherradi, and Azzouz Kchikach. 2025. "Multi-Layer Perceptron Neural Networks for Concrete Strength Prediction: Balancing Performance and Optimizing Mix Designs" Engineering Proceedings 112, no. 1: 1. https://doi.org/10.3390/engproc2025112001
APA StyleAlouan, Y., Cherif, S.-E., Kchakech, B., Cherradi, Y., & Kchikach, A. (2025). Multi-Layer Perceptron Neural Networks for Concrete Strength Prediction: Balancing Performance and Optimizing Mix Designs. Engineering Proceedings, 112(1), 1. https://doi.org/10.3390/engproc2025112001






