Synergic Impact of Reinforcement Learning and Swarm Intelligence in Wireless Sensor Network Services ^†

Abstract

Wireless sensor networks (WSNs) consist of distributed sensor nodes deployed for real-time monitoring and data collection. Optimizing sensor energy consumption is critical for extending the overall network lifespan. In large-scale WSNs, clustering techniques are required to reduce energy consumption. Many effective clustering methods have been proposed, but finding the optimal number of clusters in an energy-efficient manner remains challenging. Swarm intelligence (SI) algorithms help solve this problem, but testing all possible cluster configurations is computationally expensive. Neural networks excel in identifying hidden patterns in data, making them a promising tool for this task. However, training an AI agent to accurately predict both the number of cluster heads (CHs) and their locations is difficult. In this study, we developed a synergic method by employing a reinforcement learning (RL) model to predict the number of CHs while utilizing an SI algorithm to identify the most appropriate nodes to become CHs. This approach minimizes transmission energy and prolongs the lifespan of WSNs and their services.

1. Introduction

Wireless sensor networks (WSNs) are essential in various applications, including environmental monitoring, smart agriculture, and industrial automation. These networks comprise spatially distributed sensor nodes that collect, process, and transmit real-time data. However, one significant challenge due to the sensors’ limited energy source is energy management. This issue arises because the sensor nodes are usually battery powered and often deployed in environments where frequent maintenance or replacing batteries is impractical.

Clustering techniques have emerged as a widely adopted strategy to enhance energy efficiency and extend the operational lifespan of WSNs [1]. Organizing nodes into clusters, with designated cluster heads (CHs) responsible for aggregating and transmitting data to a central base station, significantly reduces the overall communication overhead and global transmission energy. However, the performance of clustering-based energy management hinges on a critical factor: determining the optimal number and placement of cluster heads. An excessive number of clusters leads to redundant communication. At the same time, too few can overwhelm individual CHs with increased intra-cluster communication. Both of these results in sub-optimal energy usage and a reduction in WSN lifespan. Hence, the problem needs to be formulated as an optimization problem to balance between the CH numbers and their locations by considering node locations, their energies, and the global energy utilization of a proposed solution.

Various swarm intelligence (SI) methods have been proposed to address this optimization problem [2]. SI algorithms take inspiration from the behaviors observed in natural swarms, offering a practical framework for solving complex optimization challenges. However, these algorithms often face high computational complexity when applied to large-scale WSNs, which diminishes the energy savings they are designed to achieve. The growing use of machine learning and neural networks provides new solutions for optimizing energy use in WSNs. Neural networks are particularly good at identifying complex, nonlinear patterns in data. However, training these networks to accurately predict both the number and optimal placement of CHs presents their challenges.

We developed a hybrid solution that balances prediction accuracy and computational efficiency. Specifically, we utilized a neural network to estimate the optimal number of CHs based on sampling network data, namely, sensor node location and energy distributions. Subsequently, a swarm intelligence algorithm was used to identify the most energy-efficient nodes to fulfill the role of CHs. The solution minimizes transmission energy and prolongs the network’s lifespan, offering a practical and scalable solution for energy-aware clustering in WSNs.

2. Background and Related Work

In this study, we used the low-energy adaptive clustering hierarchy (LEACH) clustering protocol implementation, SI algorithms, and the proximal policy optimization (PPO) reinforcement learning agent model.

2.1. WSN Clustering

The LEACH protocol [3] is one of the earliest efficient, low-overhead clustering protocols proposed. It features decentralized coordination for clustering and CH selection, requiring minimal additional data transfer between the base station (BS) as the newly elected CH transmits the election updates to its neighbors. Due to its simplicity, scalability, and robustness in dynamic network environments, LEACH is widely used. Nowadays, it is often combined with other methods to improve its performance. A number of different proposals were presented in Refs. [4,5], in which clustering was combined with meta-heuristic approaches.

2.2. SI

SI [6,7] is a class of bio-inspired meta-heuristic algorithms for global optimization problems. It was constructed referring to the collective behavior observed in natural swarms, whether biological, such as flocks of birds, or physical phenomena, such as gravity or particle swarms. In SI, intelligence emerges not from the capabilities of individual agents each of which is typically simple and limited but from their collective interactions and decentralized coordination. In swarm-based optimization algorithms, each agent represents a potential solution to the problem at hand, and the quality of these solutions is assessed using a predefined fitness function (FF). The swarm collectively explores the problem space (landscape), converging toward an optimal solution. Over the years, these algorithms have proven their efficiency in many optimization problems [6,7,8]. The Bald Eagle Search optimization (BES) [9] was chosen as the complementary SI algorithm in this study.

2.3. Reinforcement Learning (RL) and Neural Networks (NNs)

The process of RL [10] is based on the principles of operant conditioning in animal behavior, where learning occurs through interaction with an environment and receiving feedback through rewards or penalties. RL focuses on how intelligent agents take sequences of actions in dynamic and often uncertain environments to maximize cumulative rewards over time. The RL process is formalized using the Markov Decision Process (MDP), which provides a mathematical structure to model the interaction between the agent and the environment. It incorporates states, actions, transition dynamics, and reward functions [3]. Through iterative exploration and exploitation, RL enables agents to learn policies that help them achieve long-term objectives without explicit supervision.

Neural networks (NNs) are computational models designed to mimic the structure and function of the brain and its neurons, enabling them to learn complex patterns and representations from data. Deep RL [11] combines multilayer neural networks with reinforcement learning principles, enabling agents to learn effective decision-making policies directly from sensory inputs.

PPO [12] is a widely utilized and highly successful deep RL algorithm with strong performance across various complex tasks. It is part of the family of policy gradient (PG) methods, which update an agent’s policy using an estimator of the gradient of the expected return. A key challenge in PG-based approaches is selecting an appropriate step size for updating the policy. A too-large step leads to significant policy degradation. At the same time, a too-small step slows learning. PPO addresses this issue with a simple yet effective clipping mechanism that constrains policy updates within a safe range [12]. This design reduces algorithmic complexity and enables efficient first-order optimizers, including gradient descent, making PPO stable and practical for large-scale applications [12].

3. Proposed Model

The model (AISI) developed in this study incorporates an RL AI agent that works in conjunction with an SI algorithm. The agent was trained to predict the number of CHs by analyzing the WSN state. Based on the number of CHs predicted by the agent, an SI algorithm determines the best nodes to serve as CHs. The WSN, as a grid, is divided into distinct regions. The agent observes the number of active nodes and their combined available energy levels at each region. A hyperparameter of the AISI model is τ, which indicates the number of observation regions.

As opposed to using the nodes’ coordinates and energy levels as direct inputs for the agent, the advantage of the setup with observation regions is its independence from the number of nodes. In other words, the agent only has to be trained once and can be utilized for different-sized WSNs, especially for higher node counts than that used in the training.

CH’s proportion is 5% of the active nodes in LEACH-based models. While this may not be the optimal number for every scenario during the WSN’s lifespan, it generally provides satisfactory solutions. The number of CHs is variable in the AISI model, and it is the agent’s role to determine this based on the actual state of the WSN at any given time a CH selection is required. Further clamping is applied to the prediction to handle bad prediction cases.

4. Simulation

The setup of the AISI model and its components during the simulations are as follows. The simulation was conducted using MATLAB R2024b.

4.1. WSN Landscape

We compared AISI and the classic LEACH models on three WSN scenarios with 50, 100, and 150 nodes, all with a starting energy of 1 J. For all scenarios, we used a 200 × 200 grid. The sensor nodes were randomly placed throughout the area, with the BS (sink) located at the center, specifically at coordinates (100, 100). We considered valid placements for the sensor nodes to be those at least 5 m from the BS. Nodes positioned close to the BS consumed minimal power and, therefore, outlasted the others, significantly prolonging the WSN lifetime in the simulations. In LEACH and AISI models, we connected the nodes based on their distance to either the closest CH or the BS itself.

4.2. AI Agent

For the AI agent, we used the MATLAB built-in PPO reinforcement learning model. For testing, we used a value of 16 for τ, meaning a grid of 4 × 4 observation regions. The values observed were regarded as the agent inputs, while the proposed number of CHs was the output. Figure 1 presents the neural network layout, which has 77.8 k learnable parameters. We restricted this predicted value to an interval between 5 and 15% of the active nodes. If the predicted value fell outside this range, we calculated the new proposed CH number using the average of the last three values, if available, or else we clamped it. In WSNs, the state st at time step t can be defined as a vector comprising of the node count and residual energy levels in each grid section, as defined in Equation (1).

$$s_t=\left\{\right(G_i, E_i)\mid i=\mathrm{1,2},...,\mathsf{\tau }\}$$

(1)

where $G_i$ denotes the number of active nodes in region $i$, $E_i$ is the total residual energy in $G_i$, and $\tau$ is the model hyperparameter denoting the number of regions.

The state transition in our case is shown in Equation (2).

$$s_{t+1}=T(s_t ,a_t)=\left\{\right(G_i,E_i-\Delta E_i\left(a_t\right)) \mid i\in 1, 2,...,\mathsf{\tau }\}$$

(2)

where $\Delta E_i$ is the energy decrease in the associated region $G_i$.

The $r$ reward function is presented in Equation (3).

$$r_t=\left(E-\Delta E_i\right)-\beta · {\overline{N}}_t$$

(3)

where ${\overline{N}}_t$ denotes the number of dead nodes in step t, and $\beta =0.99$ is a hyper-parameter proportional to the initial energy values used in the simulations.

The training was conducted by simulating the WSN with the SI optimizer during multiple 1000-episode sessions with a maximum of 200 steps per episode. Under- and over-proposals were also penalized. A training epoch was considered completed when either the maximum number of steps was reached or the WSN depleted all its energy. Upon completing an epoch, the agent received an additional reward in the form of $\gamma ·L$, where $L$ denotes the lifespan of the WSN. Initial energy levels between 0.1 and 1.0 J were used for the sensor nodes, which were set at the start of each epoch.

4.3. Energy Calculations

In a sensor node, most of the power is consumed by the operation of the transmission circuit, which increases with the distance the signal must travel. We used the multipath model formula (Equation (4)) to calculate the power usage.

$$E_{tx} \left(k,d\right)=E_{elec}\cdot k+E_{amp}\cdot k\cdot d^b$$

(4)

where $b = 2$ if $d < d_0$, and 4 [13], and $d_0$ is $87 \mathrm{m}$. Above the threshold $d_0$, there is a significant transmission power increase. We chose the 200 × 200-sized grid for this effect to be more predominant and the effectiveness of clustering to have a significantly higher impact on the results.

WSN simulation was conducted in episodes. In each episode, the power requirements for transmitting one sensor reading per node were calculated. The total energy usage in one simulation episode is an important metric of the quality of the WSN clusterization, where a lower sum indicates a more optimal configuration. We only accounted for a node’s required energy usage if it had the energy necessary to transmit. Otherwise, the node depleted its energy reserves and was considered dead.

4.4. CH Count Effect on WSN

As mentioned before, in LEACH models, generally, 5% of the active nodes were selected as CHs. However, this is not always the optimal number (Figure 2). The optimal number changed with the number of active nodes, energy levels, and distances between them. As a node’s transmission energy was summed up if the transmission was made, we did not observe the energy increasing past the optimal number of CHs but an increase in the number of dead nodes.

4.5. SI

The SI algorithm’s input was the WSN nodes and the number of predicted CHs. The goal was to choose the best nodes to serve as CHs to minimize transmission energy consumption. Since transmission power is directly related to the transmission distance, we used a strictly distance-minimizing fitness function for simplicity. With this, SI minimized the overall distance between nodes and CH and the CH—BS distance (Equation (5)). While this approach is efficient enough, a more optimal energy-aware FF needs to be determined in further research.

$$FF=\alpha \cdot \sum _{i \in N}d\left(x_i,x_{ch}\left(i\right)\right)+\left(1-\alpha \right)\cdot \sum _{j \in M}d\left(x_j,x_{BS}\left(j\right)\right)$$

(5)

where $d$ is the Euclidean distance, $N$ is the set of regular nodes, $M$ is the set of CHs, $x_{ch}\left(i\right)$ denotes the closest CH to the $i$-th node, and $\alpha \in [0\dots 1]$ is a weight factor to balance intra-cluster and CH-to-BS distances.

4.6. Simulation Parameters

Table 1. Simulation parameters.

Model Part	Setting
	Parameter	Value
Agent	τ (tau)	16
	β (beta)	0.99
SI	Algorithm	BES
	α (alpha)	0.6
	Population	10
	Maximum number of iterations	100
AISI	CH (min)	5%
	CH (max)	15%

presents the parameter values used to conduct the simulations.

5. Results

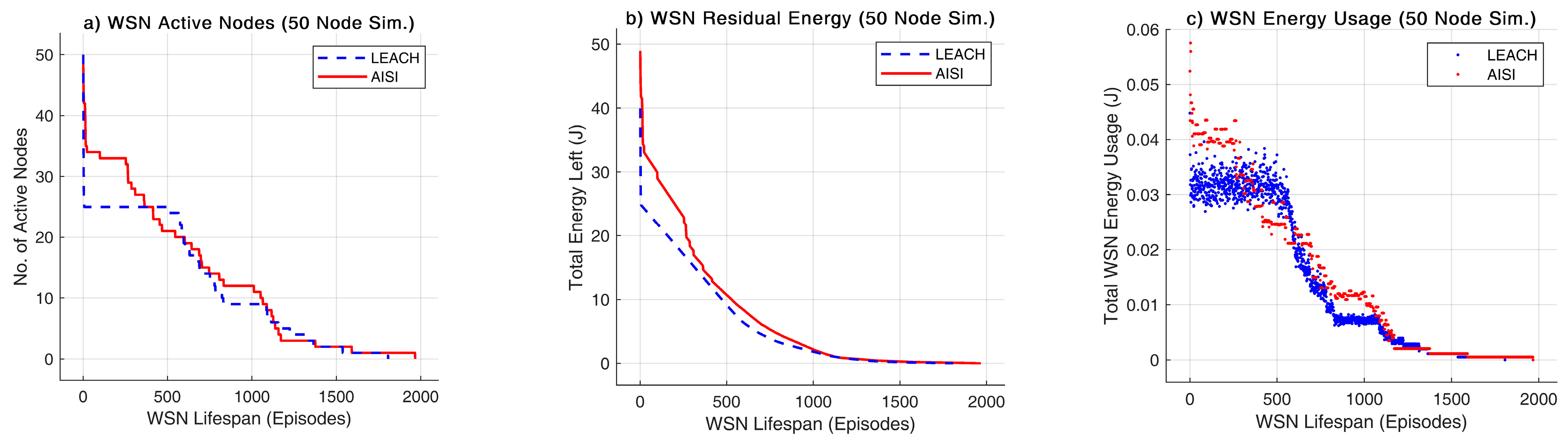
We interpreted the experimental results using multiple criteria, such as the WSN lifespan, residual energy, and energy usage. With 50 nodes and using the LEACH model, the WSN had a lifespan of 1807 without AISI and 1967 episodes with AISI. The increase rate was 8.85%. Figure 3 shows the outcomes of the two methods by the number of active nodes and residual energy. Even though the number of active nodes was similar (Figure 3a), the residual energy of the WSN (Figure 3b) was higher with the AISI model, thus increasing the network’s lifespan.

Figure 3c presents the energy usage of the sensor nodes in each step. The AISI model had a larger initial energy usage due to more active nodes in the network. At around iteration 500, the number of active nodes with both methods equaled, and the AISI model used less energy due to the SI optimization. Therefore, the energy usage with the AISI model was higher due to the higher active node count. With 100 nodes, LEACH WSN’s lifespan was 2503 episodes, while with AISI, it was 2780, which is an increase of 11.07% (Figure 4).

In the simulation with 150 nodes, the lifespan of the WSN with LEACH was 3566 episodes, while with AISI, it was 4348, which is an increase of 21.93%. Figure 5 compares the active number, residual energy, and energy usage (Figure 5).

When comparing the simulation result criteria, a similar pattern in all test scenarios was observed (Figure 3, Figure 4 and Figure 5). Due to the SI optimizer, AISI kept a higher number of nodes active (alive) and therefore had a higher initial energy usage. In all three cases, at around episode 500, the active node count was equal to that of the other. However, the AISI extended the WSN’s lifespan due to the higher residual energy accumulated by this point.

Table 2. Combined simulation results.

	Simulation Scenario
Nodes	50	100	150
Model	WSN Lifespan (Episodes)
LEACH	1807	2503	3566
AISI	1967	2780	4348
Increase in rate	8.85%	11.07%	21.93%

presents the combined results of the simulations. In the three scenarios, both models’ performance increased as the sensor density increased, but the AISI model showed a more significant benefit. In the 150-node scenario, only the CH number prediction provided by the agent resulted in a 5% extension of the network’s lifespan. When we applied the SI optimization, a 10% improvement in performance was observed. However, when combining the two, a 21.93% increase in the WSN’s lifespan was obtained.

6. Conclusions

In this study, we developed the AISI model, which combined an AI agent with SI optimization to enhance the lifespan of WSNs. The agent predicts the number of CHs required from observing the current state of the WSN, while the SI component selects the most suitable nodes for this role. We tested the model through simulations in multiple scenarios, and we observed improvements in the WSN’s lifespan, especially in the case of denser networks. It is still necessary to explore additional enhancements of the agent to improve the AISI model’s performance.