An Approach to Prediction Using Networked Multimedia †
Abstract
1. Introduction
- Description—display of summarized statistics and graphical representation.
- Analysis and interpretation—finding a model that describes the time dependence in the data.
- Prediction—given a sample from the series, the next value or the next few values are predicted.
2. Methodology
- Moving the average method—Averages are calculated for large adjacent data for a certain number of members of the series and the averaging process is successively moved.
- Method of average growth and average rate—This is applied when there are sufficient grounds to assert that development has the character of arithmetic or geometric progression. The data can be aggregated in advance.
- Graphical method—This is used for illustration and analysis. At the discretion of the researcher, a line is drawn closest to the empirical one and its values are considered on the y-axis scale, which are taken as smoothed (equalized) values for the time series.
- Analytical method (least squares method)—This is the most advanced method for aligning dynamic series. It includes the following:
- (a)
- Choosing a pattern expressing the trend.
- (b)
- Determination of the symbols of the periods.
- (c)
- Determination of the mathematical expression of the function by which the main trend will be described. Depending on the specific case, the following basic models can be applied.
- (d)
- Determination of the parameters of the equations, the model of which is chosen in specific cases.
- (e)
- Determination of the values of the trend model, i.e., the estimates, by substituting the symbols in the equation expressing the main trend
- (f)
- Verification of the correctness of the calculation procedures.
3. Linear Trend Pattern
4. Nonlinear Trend Patterns: Converting Nonlinear Models to Linear Models
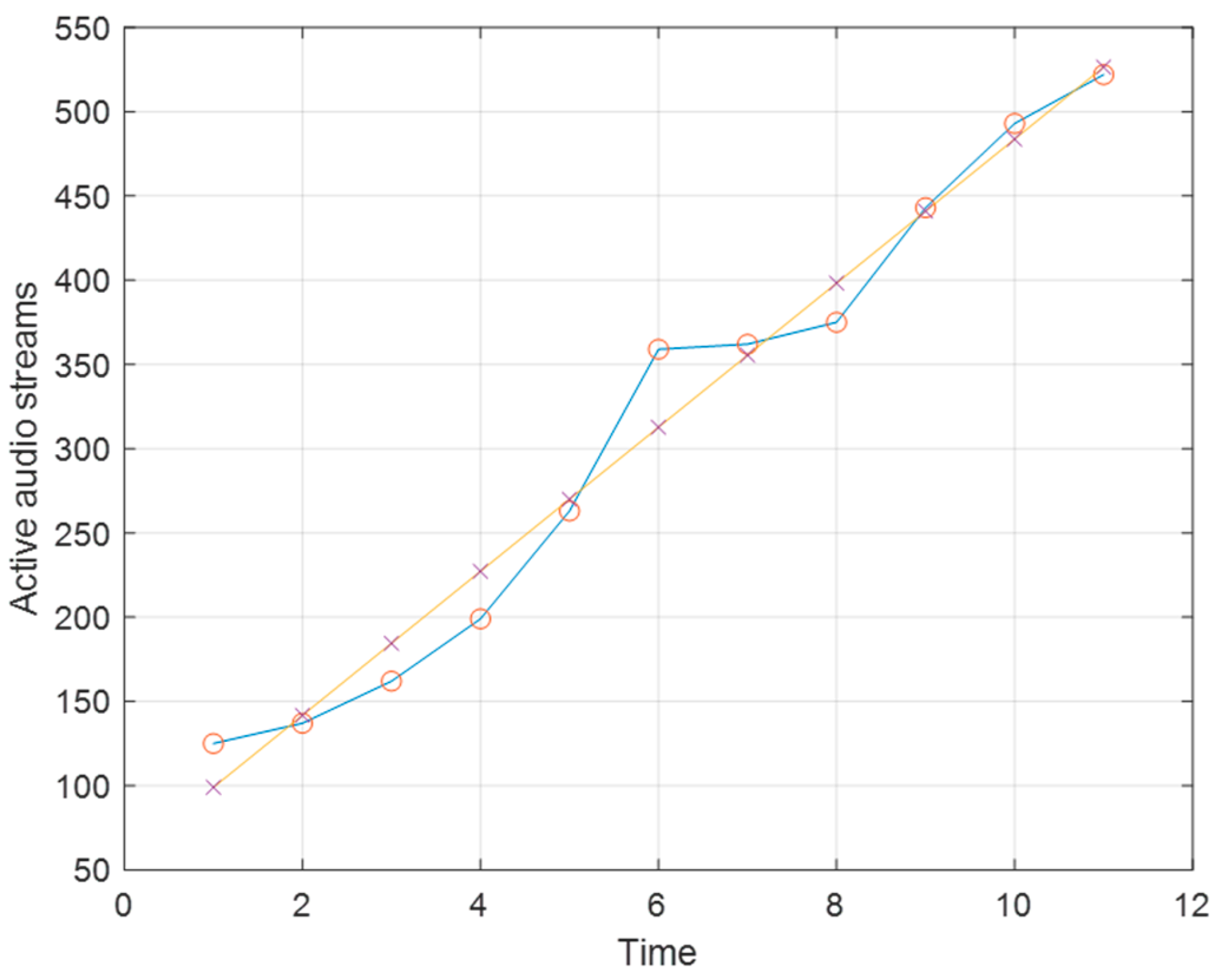
5. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hess, A.; Iyer, H.; Malm, W. Linear trend analysis: A comparison of methods. Atmos. Environ. 2001, 35, 5211–5222. [Google Scholar] [CrossRef]
- Puri, A. Multimedia Systems, Standards, and Networks; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Li, Y.; He, Z.; Zhang, Q. Fast Decision-Tree-Based Series Partitioning and Mode Prediction Termination Algorithm for H.266/VVC. Electronics 2024, 13, 1250. [Google Scholar] [CrossRef]
- Han, C.; Zhang, S.; Zhang, B.; Zhou, J.; Sun, L. A Distributed Image Compression Scheme for Energy Harvesting Wireless Multimedia Sensor Networks. Sensors 2020, 20, 667. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J. Multimedia Networking: From Theory to Practice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- He, Z.; Gao, S.; Xiao, L.; Liu, D.; He, H. Multimedia Data Modelling Using Multidimensional Recurrent Neural Networks. Symmetry 2018, 10, 370. [Google Scholar] [CrossRef]
- Lee, T.-S.; Wang, C.-H.; Yu, C.-M. Fuzzy Evaluation Model for Enhancing E-Learning Systems. Mathematics 2019, 7, 918. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2011, 17, 1042–1046. [Google Scholar] [CrossRef]
| Trend Type | Mathematical Model |
|---|---|
| Linear | |
| Quadratic | |
| Cubic | |
| Hyperbolic | |
| Fractional–rational | |
| Logarithmic | |
| Exponential | |
| Power model | |
| Combined |
| Server | Meet1 | Meet |
|---|---|---|
| CPU | 2x AMD EPYC 7402 24 Core Processor | 4x Intel(R) Xeon(R) CPU E7-4820 @ 2.00 GHz Total Cores 8 |
| RAM | 64 GB Registered ECC DDR4 | 128 GB DDR3 ECC Registered memory |
| Ethernet | 2 1 GbE LAN via Intel® i350-AM21 | Intel® 82576 Dual-Port Gigabit Ethernet Controller |
| Video | ASPEED AST2500 BMC graphics | Matrox G200 eW 16 MB DDR2 |
| CPU | 2× AMD EPYC 7402 24 Core Processor | 4× Intel(R) Xeon(R) CPU E7- 4820 @ 2.00 GHz Total Cores 8 |
| RAM | 64 GB Registered ECC DDR4 | 128 GB DDR3 ECC Registered memory |
| Ethernet | 2 1 GbE LAN via Intel® i350-AM21 | Intel® 82576 Dual-Port Gigabit Ethernet Controller |
| Video | ASPEED AST2500 BMC graphics | Matrox G200 eW 16 MB DDR2 |
| Storage | SATA3 (6 Gbps) (2× NVMe on PCi) | 6 Gb/s SAS/SATA ports (1× Samsung SSD 850) |
| Ubuntu 18.04.6 LTS | Ubuntu 18.04.6 LTS | |
| Software | BigBlueButton Virtual Classroom (v.2.4.4) | BigBlueButton Virtual Classroom (v.2.4.4) |
| Measurement Moment (t) | Week | Dates in 2024 | |
|---|---|---|---|
| 1 | 41 | 07.10 | 13.10 |
| 2 | 42 | 14.10 | 20.10 |
| 3 | 43 | 21.10 | 27.10 |
| 4 | 44 | 28.10 | 03.11 |
| 5 | 45 | 04.11 | 10.11 |
| 6 | 46 | 11.11 | 17.11 |
| 7 | 47 | 18.11 | 24.11 |
| 8 | 48 | 25.11 | 01.12 |
| 9 | 49 | 02.12 | 08.12 |
| 10 | 50 | 09.12 | 15.12 |
| 11 | 51 | 16.12 | 22.12 |
| Trend Type | Sample Period/Forecast Period | Estimated Value | Real Value | Absolute Error |
|---|---|---|---|---|
| Linen | 07.10–15.12/ 16.12–22.12 | 526.50 | 522 | 4.50 |
| Quadratic | 07.10–15.12/ 16.12–22.12 | 530.36 | 522 | 8.36 |
| Cubical | 07.10–15.12/ 16.12–22.12 | 517.48 | 522 | 4.52 |
| Hyperbolic | 07.10–15.12/ 16.12–22.12 | 385.81 | 522 | 136.18 |
| Fractional–rational | 07.10–15.12/ 16.12–22.12 | 365.22 | 522 | 156.78 |
| Logarithmic | 07.10–15.12/ 16.12–22.12 | 456.06 | 522 | 65.94 |
| Exponential | 07.10–15.12/ 16.12–22.12 | 1,747,574.94 | 522 | 1,747,052.94 |
| Steepened | 07.10–15.12/ 16.12–22.12 | 499.11 | 522 | 22.89 |
| Combined | 07.10–15.12/ 16.12–22.12 | 310.24 | 522 | 211.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hinkov, V.; Krastev, G. An Approach to Prediction Using Networked Multimedia. Eng. Proc. 2025, 104, 90. https://doi.org/10.3390/engproc2025104090
Hinkov V, Krastev G. An Approach to Prediction Using Networked Multimedia. Engineering Proceedings. 2025; 104(1):90. https://doi.org/10.3390/engproc2025104090
Chicago/Turabian StyleHinkov, Vladislav, and Georgi Krastev. 2025. "An Approach to Prediction Using Networked Multimedia" Engineering Proceedings 104, no. 1: 90. https://doi.org/10.3390/engproc2025104090
APA StyleHinkov, V., & Krastev, G. (2025). An Approach to Prediction Using Networked Multimedia. Engineering Proceedings, 104(1), 90. https://doi.org/10.3390/engproc2025104090





