A Reinforcement Learning Solution for Queue Management in Public Utility Services ^†

Abstract

This paper presents a reinforcement learning-based approach for optimizing queue management in public utility service environments. Using one year of real operational data from a utility office, a simulation model is developed to replicate daily service dynamics. A Q-learning agent is trained to allocate service types to counters dynamically, aiming to minimize client waiting time. The model treats the environment as a Markov Decision Process and uses an epsilon-greedy policy for learning optimal actions. Experimental results across multiple counter configurations demonstrate significant reductions in average waiting times, confirming the effectiveness and adaptability of the proposed method in dynamic service environments.

1. Introduction

The effective management of queues is a challenge for each entity dealing with large numbers of clients, patients, or visitors. The solutions vary widely, but most often they refer to queueing theory, rooted in the field of telecommunications and traffic engineering. It suggests that a model can be built so that waiting times and queue lengths could be predicted [1,2]. Given the vast diversity of fields as well as the specificities of each organization, the models, and their respective queueing strategies, formulating an adequate solution in each separate case could be different.

For services like emergency medical departments, overcrowding could have significant consequences not only on the patients’ dissatisfaction but also on their health, and it can often be crucial for saving one’s life. In such cases, issues like prioritizing cases and services is of primary importance [3]. On the other hand, in services like recreation and entertainment (e.g., theme parcs) [4], the factors driving queue-related decisions could be based on clients’ satisfaction (or the company’s expected profit) and can sometimes allow waiting in the queue above some thresholds, compensated with a service of “great value” for the customer. However, the seasonal peaks of these services and group visits [5] could impose queue-optimization strategies based on a completely different logic.

In the context of public utility services, where the perceived added value of waiting is often limited, ensuring a smooth and time-efficient service experience becomes essential for maintaining user satisfaction. To achieve this, the selected queuing model in each specific case should be informed by several key factors, outlined as follows: the estimated number of clients per day, the range of services provided by the entity, and the average processing time for each service; the number of counters/points of service (or servers, based on the queueing theory terminology) working in parallel; and the allocation of services or how they are distributed by counters and so on. Another issue is the number of queue stages, as well as the underlying principle of the service regarding the client stack.

Taking all these factors into account, in the current paper we propose a solution for the optimization of the average waiting time in a queueing system with several parallel working queues in a one-stage service scenario, which can be applied to a number of facility services. We base our solution on one-year real data recordings, a software simulation of the process, and the implementation of a reinforcement learning algorithm.

2. Method

2.1. Method

The current paper bridges the gap between traditional queueing theory and reinforcement learning, introducing an innovative, real data-driven approach for optimizing service allocations in dynamic queue environments (Figure 1).

The queueing system architecture (Figure 2) consists of a common client stack where the clients wait to be recalled for service, there is a known number of counters, and the allocation of services can vary in order to ensure the most effective process, optimizing the average waiting time. The processing of the stack generally follows the First In First Out (FIFO) rule, also known as First Come First Served (FCFS).

Unlike conventional queueing systems with fixed service assignments, this model leverages reinforcement learning to adaptively allocate counters based on real-time client arrivals and variable processing times. The allocation strategy is based on a learned service assignment policy, where each counter dynamically selects one service type to prioritize at each time step. All counters are equally capable of serving any request type, and the model uses Q-learning to optimize these assignments based on queue dynamics and system performance over time. The integration of real client arrival distributions and service time variability allows the Q-learning model to learn from empirical queue behavior, enhancing its real-world deployment potential.

2.2. Data

Data were gathered from an authentic source, more specifically, one of the offices of public utility Company X, over the course of a single calendar year. The dataset encompassed all clients served and all services rendered by the entity, including details such as arrival times, waiting durations, processing times, and the allocation of services and clients across operational counters.

2.3. Simulation

Subsequently, a simulation model was developed, incorporating input variables based on the real data extracted. The objective of the simulation was to replicate a process characteristic of a public utility service office. The model computes the average waiting time per client as this parameter is of paramount importance and is targeted for optimization.

2.4. Reinforcement Learning Model

In reinforcement learning models, an agent interacts with a specific environment in order to learn by their own experience and find the best decision-making policy. In our case we implemented a Q-learning algorithm (the agent), which interacted with the environment presented as a Markov Decision Process (MDP). The MDP could be described as follows:

• States S: Representing all possible queue configurations (how service counters are allocated to different service types);
• Actions A: Decisions regarding the allocation of services throughout counters;
• Transition function P(s′∣s,a): Probability of moving from state s to state s′, given action a.
• Reward function R(s,a): Defines the immediate feedback for taking action a in state s.
• Discount factor γ: Balances future rewards vs. immediate rewards.

Since transitions depend on a probabilistic distribution (implemented in the script), the process follows the Markov property, outlined as follows: the next state only depends on the current state and action, not the past history. The reward function combines the following three components: a core efficiency term that penalizes deviation from the target queueing and waiting times, a stability penalty to discourage extreme operating conditions or counter misconfiguration, and a per-day penalty applied to any unserved clients, expressed as follows:

R(s,a) = R_efficiency + R_stability − P_unserved

(1)

This approach guides the agent toward configurations that are both effective and service complete.

The agent (Q-learning algorithm) observes the current state s and chooses an action a following the epsilon-greedy policy for balancing between exploration and exploitation. It explores a random action with probability ε (initially 1, decaying over time) or exploits the best action known thus far from the Q-table with probability 1 − ε. After executing an action, the agent receives a reward based on the queue’s response. Then it updates the Q-value using the Bellman equation, expressed as follows:

Q(s,a) = (1 − α)Q(s,a) + α [R + γ max_a′ Q(s′,a′)],

(2)

where the following hold:

• α—learning rate (controls update speed);
• R—immediate reward;
• γ—discount factor;
• max_a′ Q(s′,a′)—best estimated future reward.

After updating the Q-value, the agent moves to the next state, s′. The process repeats until it meets the max iteration criteria.

3. Experimental Results

3.1. Extracted Data

The data we used were collected during an interval of almost one calendar year from the middle of February 2024 to the end of January 2025 from one of the offices of Company X and presents the whole period since the ticketing system was adopted.

A summary of the extracted and analyzed data is presented in

Table 1. Extracted data.

Parameter	Value
Average daily clients	247
Number of the services provided by the entity	7
Distribution of clients across services	[0.22, 0.19, 0.15, 0.20, 0.05, 0.11, 0.08]
Average processing time for service i (min.)	[7, 7, 9, 10, 11, 12, 20]
Total number of counters operating concurrently	12
Mean interval time for client arrivals (min.)	2.3
Standard deviation of interval time	0.03
Average waiting time (min.)	8.21
Average total time in the system (min.)	19.16

.

3.2. Implementation

The agent and the simulation environment were implemented in Matlab R2016a. The hyper-parameters of the model are depicted in Figure 1 along with their adjusted values.

The input parameters (Figure 3) were taken from the analysis of the extracted data, whereas the hyper-parameters of the Q-learning agent were experimentally adjusted. The number of iterations were chosen so as to represent the working hours (8 h or 480 min per day) over 20 days (roughly the number of working days in one calendar month). Each iteration represents a minute, after which the agent checks for free counters and suggests which service to allocate to them, implementing the FIFO principle for the clients chosen for the respective service.

3.3. Results

Four scenarios with, respectively, 12, 10, 8, and 6 counters working in parallel are presented in

Table 2. Waiting, service, and total times in the system in 4 scenarios on the first and last working days.

	12 Counters	10 Counters	8 Counters	6 Counters
Day 1 Avg Pure Waiting Time (min.)	6.96	6.94	6.96	6.98
Day 1 Avg Service Time (min.)	9.63	9.36	9.04	9.52
Day 1 Avg Total Time in System (min.)	16.59	16.30	16.00	16.50
Day 20 Avg Pure Waiting Time (min.)	6.37	6.32	6.68	7.25
Day 20 Avg Service Time (min.)	9.63	9.36	9.04	9.52
Day 20 Avg Total Time in System (min.)	16.00	15.67	15.72	16.77
Avg Waiting Time Decrease (%)	8.50%	9.01%	4.04%	−3.93%

.

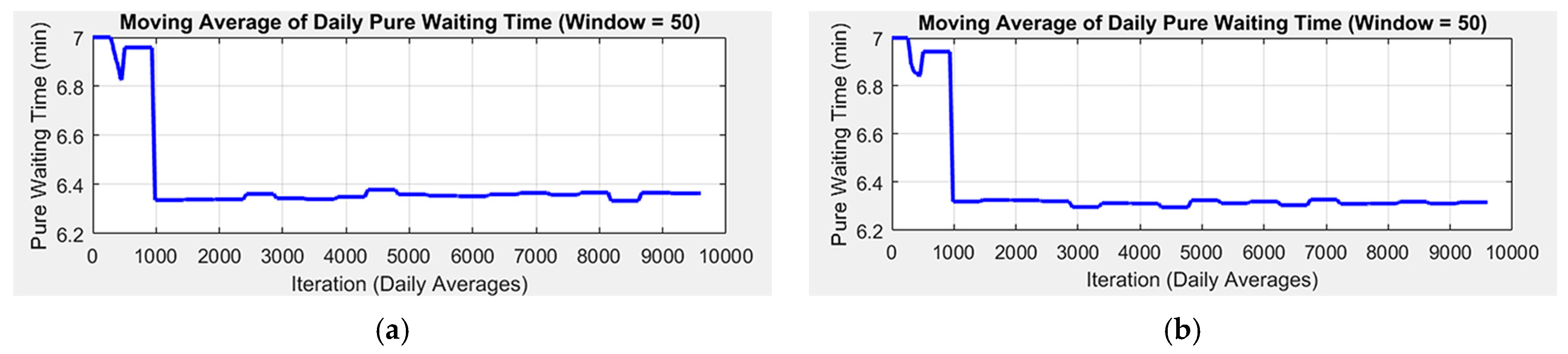
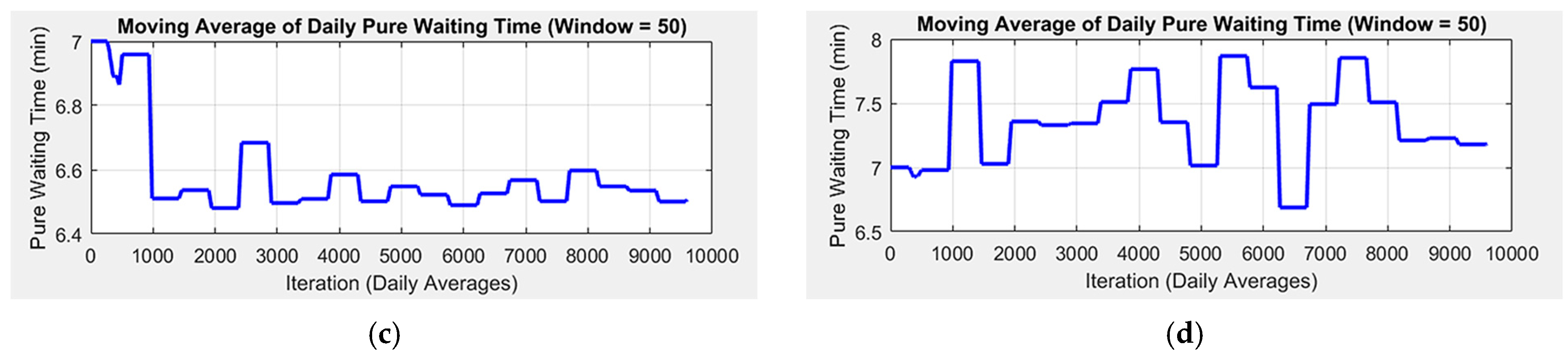
The change in average waiting time across iterations is shown in Figure 4.

The 12-counter scenario, compared to the extracted data with the same counter number performs better in terms of average waiting time and total time in the system, especially after the first 1000 iterations (roughly 2 days), when the behavior of the agent is shaped by the reward policy. The biggest decrease in percent is achieved with 10 counters (Table 2) and shows a steady behavior following initial training. Decreasing the number of counters from this point onwards causes instability in the agent’s behavior due to the insufficient operational capacity of the system and the respective unserved clients at the end of the working day.

4. Conclusions

This study presents a data-driven reinforcement learning approach, leveraging Q-learning to optimize queue management in public utility services. By modeling the service environment as a Markov Decision Process and training the agent on real operational data, the system effectively reduces average client waiting times while dynamically adapting to varying workloads and resource constraints. The results demonstrate that the learned policies outperform baseline allocations across multiple counter configurations, with the most notable improvement observed in the 10-counter scenario. The Q-learning agent exhibits stable and efficient performance after a brief training phase, confirming the method’s robustness and applicability. This approach contributes a scalable and adaptive solution for public service providers seeking to enhance efficiency and user satisfaction through intelligent queue management.