Optimization of Work Order Scheduling in Weaving Looms Using Genetic Algorithms ^†

Abstract

Efficient scheduling of work orders in weaving looms is crucial for improving production efficiency and meeting tight delivery deadlines in the textile industry. This study proposes a genetic algorithm (GA)-based model to optimize work order assignments, minimize type changeover durations, and balance machine workloads. The model uses real-world ERP data, supports job splitting for parallel production, and dynamically classifies type changes into variant, linked warp, and full setup changes. Experimental results show significant improvements in planning time, changeover reduction, and delivery performance. The proposed GA approach offers a scalable and intelligent solution that can be readily adopted for modern textile manufacturing challenges.

1. Introduction

The textile industry faces significant challenges in production planning due to increasing customer demands for customized products and shorter delivery times. In weaving operations in particular, the planning and scheduling of work orders while minimizing type changeover durations directly affect production efficiency and operational success.

Traditional manual planning methods, which rely heavily on human experience, struggle to handle the complexity and dynamic nature of modern weaving production. Scheduling must simultaneously consider tight delivery deadlines, diverse fabric specifications, and the minimization of costly type changeovers—classified into variant changes, linked warp changes, and full setup changes, each carrying different operational penalties.

Furthermore, the increasing diversity and volume of work orders complicate resource allocation and require a more dynamic approach that manual methods cannot efficiently support. Addressing these issues demands algorithmic solutions capable of optimizing multiple objectives simultaneously.

In response, this study presents a genetic algorithm (GA)-based intelligent scheduling model that optimizes work order assignment to weaving looms, dynamically minimizes type changeover durations, enables parallel production through job splitting, and ensures on-time deliveries based on real ERP production data.

The proposed model is validated using real-world operational data from a mid-sized textile factory, demonstrating significant improvements in planning time, delivery performance, and machine workload balance. The results highlight the potential of evolutionary algorithms as a robust and scalable solution for modern textile manufacturing challenges.

The effectiveness of the proposed GA model is subsequently validated on real ERP data, and the full experimental methodology and results are presented in Section 5.

2. Related Work

This section reviews state-of-the-art scheduling methods in textile production, covering heuristic dispatching rules, metaheuristic approaches, and hybrid models, and highlights their primary problem–solution characteristics and limitations.

2.1. Genetic Algorithm Foundations

Holland’s foundational work introduced Genetic Algorithms (GAs) for adaptive search [1], and Goldberg and Deb refined selection and crossover mechanisms [2] to enhance convergence. In textile scheduling:

• Wang et al. [3] encoded job sequences in a GA to minimize total tardiness, but their model did not distinguish changeover types, resulting in approximate setup time estimates.
• He et al. [4] applied an improved Ant Colony Optimization (ACO) to reduce schedule lateness, yet their approach lacked job-splitting capabilities for urgent, large orders.

2.2. Multi-Objective and Hybrid Metaheuristics

• Dai et al. [5] employed NSGA-II on synthetic weaving scenarios to balance deadline adherence and machine utilization but did not integrate real ERP data or fine-grained changeover penalties.
• Wong and Leung [6] optimized fabric utilization via GA, reducing material waste but overlooking delivery deadlines and workload balance.
• Kuehsamy et al. [7] focused on structural optimization of 3D woven preforms with GA, demonstrating design benefits but not addressing dynamic scheduling constraints.

2.3. Quality Control and Logistics Extensions

• Zhang et al. [8] combined GAs with neural networks for fabric defect detection, improving quality control without offering a unified scheduling framework.
• Cheng and Wang [9] used GAs for parameter tuning in garment design, and Kapur and Kumar [10] optimized cellular manufacturing layouts, both lacking sequential changeover modeling.
• Uzakova and Murodkhujaeva [11] and Koňařík et al. [12] enhanced transport logistics and mechanical components, respectively, yet treated production scheduling in isolation.
• Liu et al. [13] integrated condition monitoring into multi-objective GA scheduling, enhancing reliability but omitting the full spectrum of setup types.

2.4. Fuzzy and AI-Based Approaches

• Li et al. [14] introduced a fuzzy-logic GA for parallel machine scheduling under uncertainty, demonstrating adaptability but not supporting job splitting.
• Mohiuddin Babu et al. [15] explored AI-based GA systems in flexible fashion manufacturing yet confined their scope to algorithmic performance metrics without ERP-driven workflow integration.

2.5. Benchmark Heuristics

While the above methods showcase GA versatility, simple dispatching rules like EDD and SST remain widely used as control benchmarks [16]. Their inability to model complex objectives and changeover diversity motivates advanced GA-based frameworks.

2.6. Gap Analysis and Contribution

Despite extensive work on scheduling heuristics and metaheuristics, few studies integrate real factory data, model variant, linked-warp, and full setup changeovers, and enable parallel job splitting within a single framework. Our proposed GA-based model addresses these gaps by combining multi-objective fitness evaluation with dynamic type-change modeling and parallel execution on actual ERP data.

3. Materials and Methods

This section presents the dataset preparation steps, the genetic algorithm (GA) structure developed for work order scheduling, the modeling of type changeovers, and the fitness function design. The methodology was applied to real-world ERP production data and tailored to accommodate operational constraints specific to weaving loom environments.

Following the preparation of the dataset and work order parameters, a genetic algorithm (GA) structure was developed to optimize the assignment and sequencing of jobs across the available weaving looms.

3.1. Problem Definition

In weaving production systems, efficient scheduling of work orders is vital for ensuring timely deliveries, maximizing resource utilization, and minimizing production bottlenecks. However, several real-world constraints make the scheduling problem inherently complex:

• Strict Delivery Deadlines: Each work order must be completed before its designated delivery date to meet customer expectations and avoid penalties.
• Setup Changeovers: Transitioning between different work orders incurs type changeover times, categorized as variant changes, linked warp changes, or full setup changes, each with different operational costs.
• Machine Load Imbalance: Uneven distribution of work orders can lead to idle looms or overloaded machines, reducing overall production efficiency.
• Job Splitting Needs: Large work orders sometimes need to be split and processed in parallel on multiple machines to meet deadlines, introducing additional complexity in assignment.
• Production Speed Variability: Different fabric types and pick densities directly affect production speeds, requiring careful matching of work orders to machine capabilities.
• The objective is to generate an optimized schedule that assigns a set of work orders to a fixed number of weaving looms in a way that
• Minimizes the total number and duration of type changeovers;
• Ensures all work orders are completed by their respective deadlines;
• Balances the workload across all machines;
• Allows for parallel production by intelligently splitting large orders where necessary.

Formally, this constitutes a multi-objective, constraint-based scheduling problem with a combinatorially large solution space, making metaheuristic approaches such as Genetic Algorithms (GAs) particularly suitable for finding feasible and near-optimal solutions within a reasonable computation time.

3.2. Dataset and Work Order Preparation

The dataset used in this study was extracted from the ERP system of a mid-sized textile manufacturing company and includes over 1,000 weaving work orders covering one year of operational data. Each work order contains attributes such as order ID, quantity (in meters), pick density, delivery deadline, variant code, and warp group (ulak) code.

To enable parallel production across multiple weaving machines, large work orders were split into smaller segments. However, based on the operational practices of the factory, splitting was only permitted if the resulting segments exceeded a minimum threshold. In this study, the threshold was set to 500 m, consistent with the company’s internal production standards.

Production time estimations for each work order were calculated based on machine efficiency and pick density. First, the weaving speed was calculated in centimeters per minute, considering picks per minute, loom efficiency, and pick density. This value was then converted into meters per hour by multiplying by 60 (minutes in one hour) and dividing by 100 (centimeters in one meter), using the following formula:

$$Speed\left({\displaystyle \frac{\mathrm{m}}{\mathrm{h}}}\right)={\displaystyle \frac{PICS\_PER\_MIN\times \mathrm{E}\mathrm{F}\mathrm{F}\mathrm{I}\mathrm{C}\mathrm{I}\mathrm{E}\mathrm{N}\mathrm{C}\mathrm{Y}}{PickDensity}}\times {\displaystyle \frac{60}{100}}$$

(1)

where PICKS_PER_MIN = 450 picks per minute and EFFICIENCY = 0.85. The production duration for each work order was then obtained by dividing the order quantity by the calculated speed.

This preprocessing ensured that the scheduling model considered realistic production constraints and enabled dynamic workload distribution during optimization.

3.3. Genetic Algorithm Structure

A genetic algorithm (GA) was designed to optimize the scheduling of work orders across weaving looms. Each individual (chromosome) in the population represented a permutation of work order indices, defining the sequence in which jobs would be assigned to machines.

The initial population consisted of 50 individuals, generated through a combination of random sampling and deadline-sorted sequences to ensure diversity and initial feasibility. Tournament selection with a size of 3 was used as the parent selection strategy, balancing exploration and exploitation within the search space.

Genetic operators included two-point crossover with a probability of 0.7 and index shuffle mutation with a probability of 0.05. These operators introduced variability into the population while preserving useful genetic material across generations.

The evolutionary process was iterated over 20 to 100 generations depending on experimental scenarios. The objective of the GA was to evolve schedules that minimized type changeover durations, balanced machine workloads, and ensured all orders met their delivery deadlines.

Decoding of individuals into machine schedules was performed using a greedy heuristic that selected the best machine for each job based on availability, previous job type, and remaining time to deadline.

3.4. Type Change Model

In weaving operations, transitions between consecutive work orders often require different levels of machine setup adjustments, known as type changeovers. Efficient management of these changeovers is critical to maintaining production continuity and minimizing idle times.

This study considers three distinct types of type changes:

• Variant Change: Minor adjustments involving only the yarn type or pattern, requiring approximately 30 min.
• Linked Warp Change: Partial configuration replacement where warp threads are compatible, but a new warp beam is introduced, requiring approximately 120 min.
• Full Changeover: Complete reconfiguration of both warp and weft systems, requiring approximately 180 min.

Each work order includes variant and warp group (ulak) codes, which are dynamically evaluated to determine the required type change during scheduling. Correct identification and sequencing of these changes are crucial for reducing cumulative changeover time and improving overall production efficiency.

3.5. Fitness Function

The genetic algorithm employs a multi-objective fitness function to evaluate candidate schedules based on three key criteria:

• Tardiness Penalty: Measures the total delay of work orders that are completed after their delivery deadlines. Schedules with lower cumulative tardiness are favored.
• Load Imbalance Penalty: Assesses the standard deviation of total production time across all machines. More balanced machine workloads result in lower penalties.
• Changeover Cost: Calculates the cumulative time incurred by type changes (variant, linked warp, full changeovers) between consecutive jobs assigned to the same machine.

The overall fitness score is computed by combining these components with specific weights, emphasizing timely deliveries and efficient type change management. The fitness function is defined as:

$$\begin{array}{cc}Fitness=(2.0 \times & Tardiness Penalty)+\left(1.0 \times Load Imbalance Penalty\right)\\ & +(3.0 \times Changeover Cost)\end{array}$$

(2)

Lower fitness values indicate better schedules, as the objective is to minimize delays, workload imbalance, and setup transition durations simultaneously.

3.6. Parallel Production and Splitting Strategy

In order to meet strict delivery deadlines, large work orders were dynamically evaluated for parallel execution across multiple weaving machines. Based on operational practices at the factory, a minimum threshold of 500 m was established; work orders could only be split if each resulting segment exceeded this limit.

The system estimates available time windows for each machine and distributes segments accordingly, ensuring that no individual segment violates the factory’s minimum production size policy. This strategy reduces overall tardiness by allowing urgent orders to be completed faster through simultaneous production.

During scheduling, the splitting process also considers machine availability, load balancing, and type changeover minimization to maintain production efficiency. Each split segment retains its original variant and warp group information to accurately account for subsequent type changeovers.

The dynamic splitting and parallel production logic form an integral part of the optimization process, significantly enhancing the model’s flexibility in adapting to varying production demands and constraints. The overall workflow of the proposed scheduling system is illustrated in Figure 1.

3.7. Algorithm 1: Genetic Algorithm for Work Order Scheduling

The following pseudocode summarizes the main steps of the genetic algorithm used to optimize work order scheduling in weaving looms (Algorithm 1).

Algorithm 1: Genetic algorithm for work order scheduling.

Input: WorkOrders, MachineCount, Parameters (popSize, genCount, cxProb, mutProb)

Output: BestSchedule

1. Initialize population P with random permutations of WorkOrders

2. Evaluate fitness for each individual in P

3. Repeat for genCount generations:

a. Select parent pairs via tournament selection

b. Apply two-point crossover (cxProb) and mutation (mutProb)

c. Decode each offspring to a machine schedule

d. Compute fitness by summing:

• Tardiness penalties

• Changeover penalties

• Load imbalance penalties

e. Form new population from best individuals

4. Return the schedule of the individual with the best fitness

The ComputePenalties (Schedule) function calculates.

• TardinessPenalty: sum of (completionTime – deadline) for late jobs.
• ChangeoverPenalty: sum of setup times between consecutive jobs.
• LoadBalancePenalty: standard deviation of total workload across machines.
• Fitness = 2 × TardinessPenalty + 3 × ChangeoverPenalty + 1 × LoadBalancePenalty.

4. Results

This section presents the experimental evaluation of the proposed genetic algorithm (GA)-based scheduling model. The performance of the model was assessed using real ERP production data from a mid-sized textile factory, covering over 1000 weaving work orders across 25 machines. The experiments measured key metrics such as average planning time, total changeover duration, deadline compliance rate, and workload balance.

The GA-based scheduling results were compared against traditional manual planning methods to demonstrate improvements in operational efficiency, resource utilization, and delivery reliability. Tabular and graphical summaries of the findings are provided to support the analysis.

4.1. Experimental Setup

To evaluate the performance of the proposed genetic algorithm (GA)-based scheduling model, a series of experiments were conducted using real production data obtained from a mid-sized textile factory. The dataset contained over 1000 weaving work orders, covering a one-year period and involving 25 weaving looms.

As outlined in Algorithm 1, the genetic algorithm was implemented in Python 3.12.4 using the DEAP evolutionary computation framework.

Table 1. Genetic algorithm parameter settings used in the experiments.

Parameter	Value Range/Setting
Population Size	50
Generations	20–100
Crossover Probability	0.70
Mutation Probability	0.05
Selection Method	Tournament (k = 3)
Fitness Weights	[Tardiness: 2, Load Balance: 1, Changeover: 3]

summarizes the key GA parameters used during the experiments, including population size, number of generations, crossover and mutation probabilities, and selection method.

The GA configuration was tuned based on preliminary tests to ensure a balance between exploration and exploitation within the search space, while maintaining reasonable computation times suitable for practical factory operations.

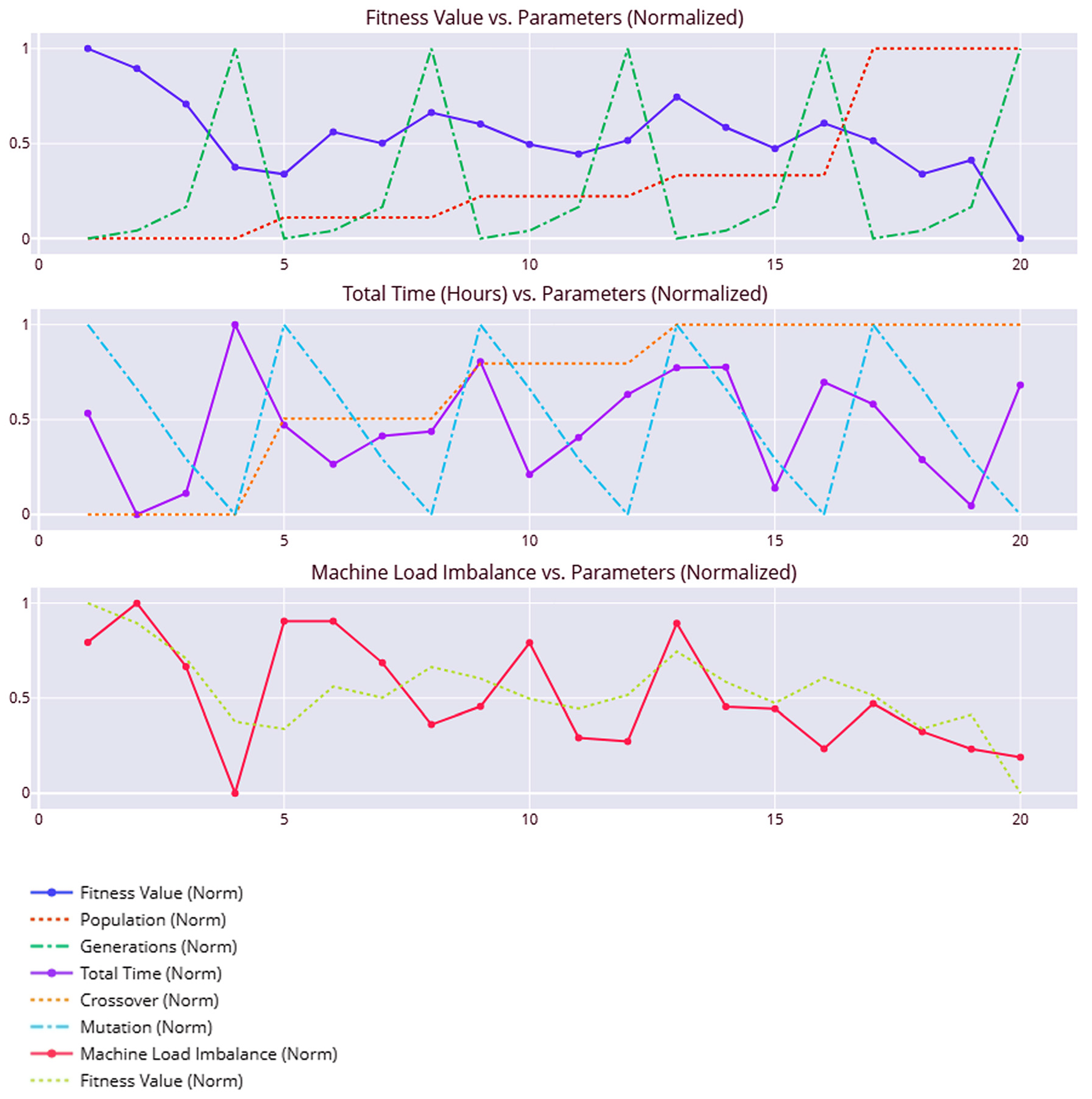
Parameter-sensitivity experiments were conducted on 20 combinations of population size (5–50) and generations (10–250) with dynamically adjusted crossover and mutation rates. The GA retained more than 90% deadline compliance across the entire design space, yet the best weighted-fitness was consistently achieved at a population size of 50 and a mutation probability of 0.05. Increasing the population above 70 or the number of generations beyond 50 yielded marginal (<3%) improvements, whereas mutation rates below 0.03 or above 0.08 degraded tardiness penalties by up to 12%. These results (Figure 2) confirm that the default configuration in Table 1 is near-optimal and that the algorithm remains robust under parameter variations.

The parameter-sensitivity plots in Figure 2 reveal three clear trends.

• Fitness improves sharply as the population size increases from 5 to 50, then plateaus, confirming that larger populations (>70) offer negligible benefit.
• Total computational time rises with generations, yet the marginal fitness gain beyond 50 generations is less than 3%, indicating a good time–quality trade-off at 20–50 generations.
• Machine-load imbalance decreases as mutation probability stabilizes around 0.05; mutation rates outside the 0.03–0.08 window cause fitness oscillations and higher tardiness penalties.

Overall, the default configuration (population = 50, generations = 50, cxpb ≈ 0.7, mutpb ≈ 0.05) lies on the Pareto knee, delivering the best weighted-fitness while keeping planning time below two minutes—supporting the robustness of the proposed GA across a broad parameter space.

4.2. Performance Metrics

To comprehensively evaluate the effectiveness of the proposed GA-based scheduling model, several key performance metrics were defined:

• Average Planning Time: Measures the total time required to generate a complete weaving schedule. A lower planning time indicates greater computational efficiency.
• Total Changeover Duration: Represents the cumulative time spent on type changeovers between consecutive work orders. Reducing this duration is critical for maximizing loom utilization and minimizing idle periods.
• Deadline Compliance Rate: Calculates the percentage of work orders completed on or before their specified delivery deadlines. A higher compliance rate reflects better operational reliability.
• Load Variance: Assesses the standard deviation of total workload assigned across all machines. Lower variance values indicate more balanced machine utilization, leading to improved resource efficiency.

These metrics provide a comprehensive view of the scheduling model’s performance, balancing computational speed, operational efficiency, and production reliability.

4.3. Comparison with Manual Planning

To assess the practical impact of the proposed genetic algorithm (GA)-based scheduling model, its performance was compared against traditional manual planning methods employed at the factory. Manual scheduling relies heavily on human experience and intuition, often resulting in suboptimal resource utilization, longer planning times, and inconsistent delivery performance.

The comparison was based on the four-performance metrics defined earlier: average planning time, total changeover duration, deadline compliance rate, and load variance.

Table 2. Comparison of manual planning and GA-based scheduling results.

Metric	Manual Planning	GA-Based Planning	EDD-Based Scheduling
Average Planning Time	~45–55 min	~1.5–2 min	~0.1–0.2 min
Changeover Duration	High (untracked)	Reduced by ~35%	Increased by ~15%
Deadline Compliance	68–72%	>90%	~85%
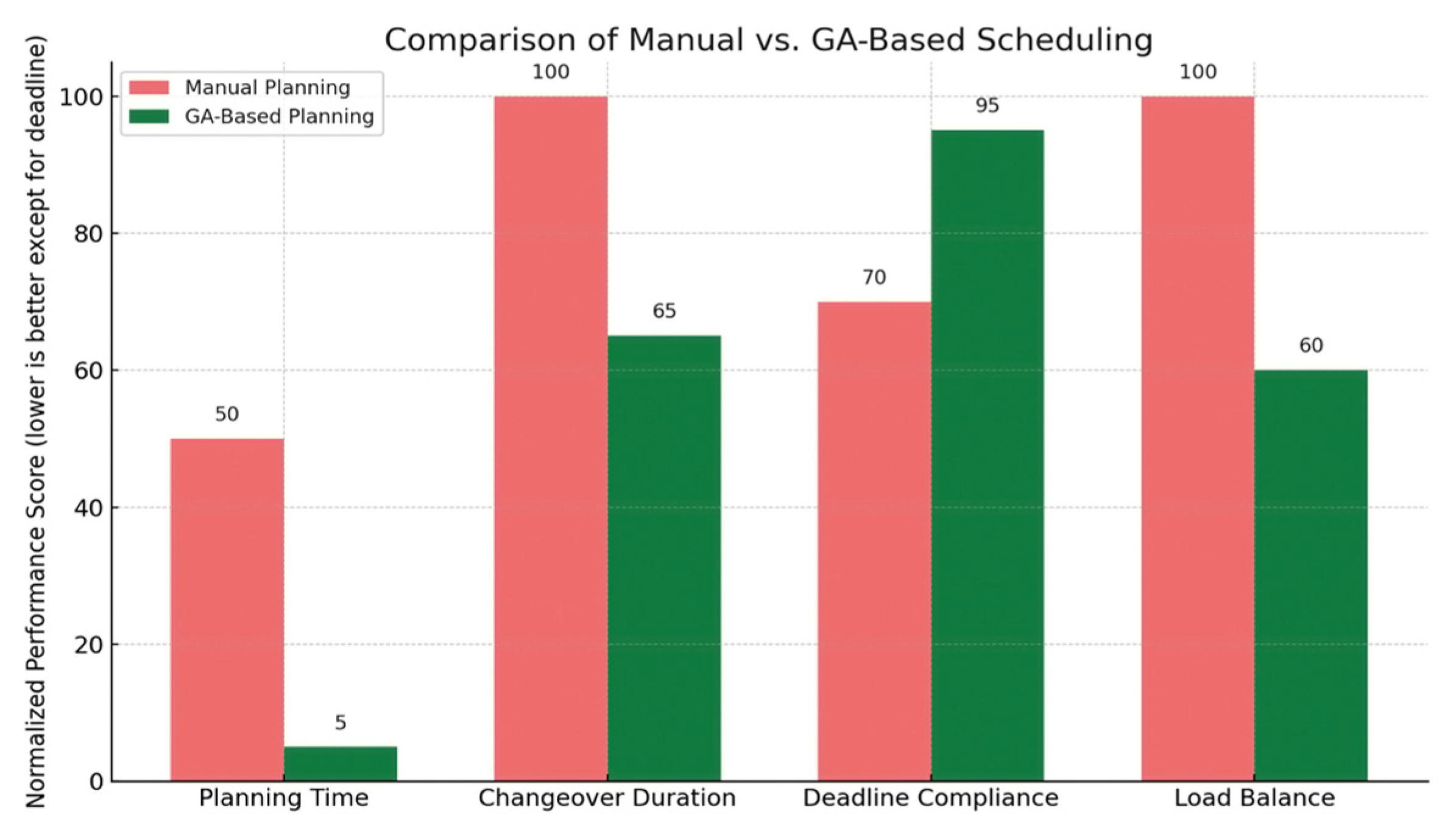
Load Balance (Std Dev)	High	Reduced by ~40%	Moderate (~25%)

summarizes the results obtained from manual planning and GA-based scheduling.

As the results indicate, the GA-based model significantly reduced planning time by over 90%, minimized cumulative changeover durations by approximately 35%, improved deadline compliance rates to above 90%, and achieved a more balanced workload distribution across machines.

As seen in Table 2, the GA-based scheduling model significantly outperforms traditional manual planning across all evaluated metrics. The proposed model reduces average planning time by more than 90%, shortens cumulative changeover durations by approximately 35%, improves deadline compliance rates to above 90%, and achieves a more balanced workload distribution across weaving machines. These results demonstrate the effectiveness and practical value of the GA-based optimization approach in real-world textile production environments.

4.4. Observations

In addition to the quantitative improvements reflected in the performance metrics, several qualitative observations were made during the experimental evaluations (Figure 3). These insights provide a deeper understanding of how the GA-based scheduling model enhances operational efficiency in weaving loom production environments:

Prioritization of Variant-Compatible Orders:

The model automatically prioritized variant-compatible orders to minimize setup delays, effectively reducing cumulative changeover times.

Effectiveness of Order Splitting:

Order splitting was particularly effective for large and urgent jobs, enabling parallel execution and better adherence to strict delivery deadlines.

Improved Machine Utilization:

The Gantt chart visualization clearly highlighted reduced idle periods and more compact machine utilization across the set of weaving looms.

5. Discussion

The experimental results clearly demonstrate that the proposed GA-based scheduling model provides substantial improvements over traditional manual planning methods in textile weaving operations. The most significant advantage observed was the dramatic reduction in average planning time, enabling more frequent and dynamic rescheduling in response to real-time production changes. Furthermore, the model’s ability to minimize cumulative type changeover durations contributed to increased machine availability and higher operational efficiency.

By automatically prioritizing variant-compatible transitions and leveraging parallel production through order splitting, the scheduling system achieved better adherence to delivery deadlines and more balanced machine utilization. These enhancements are particularly critical in high-mix, high-variability textile environments where responsiveness and flexibility are essential.

However, certain limitations were noted. The model assumes ideal machine availability and static changeover durations, which may vary in real-world production due to unforeseen factors such as machine breakdowns or operator variability. Future work will focus on incorporating real-time feedback mechanisms and dynamic adjustment of setup times to further enhance system robustness.

6. Conclusion and Future Work

In this study, a genetic algorithm (GA)-based model was developed to optimize the scheduling of work orders in weaving loom production environments. The proposed model addressed key operational challenges, including strict delivery deadlines, complex type changeovers, workload balancing, and the need for parallel production through job splitting. By incorporating real-world ERP data, dynamically modeling setup changes, and supporting large-order parallelism, the system significantly improved planning efficiency, minimized changeover durations, enhanced delivery compliance, and achieved better machine utilization compared to manual scheduling methods.

The experimental results demonstrated that the GA-based scheduling model reduced average planning time by more than 90%, decreased cumulative type change durations by approximately 35%, and increased on-time delivery rates to over 90%, while ensuring more balanced machine workloads.

To further enhance the robustness and adaptability of the system, future studies could focus on integrating real-time feedback mechanisms, such as live machine status updates or predictive maintenance signals. Additionally, dynamic adjustment of setup times based on operator performance or environmental factors, as well as the exploration of hybrid metaheuristic strategies (e.g., combining GAs with reinforcement learning or tabu search), could provide even more efficient and resilient scheduling solutions for complex textile production environments.