Experimental Study on the Influence of Load-Equalizing Devices on Planet Loads in a Planetary Gear Set ^†

Abstract

The uneven load distribution between the planets in planetary gear trains has found multiple solutions including high manufacturing precision, targeted compliance or kinematic mobility of the components of the gear train. This paper presents an experimental investigation of the influence of three different load-equalizing devices on planetary gears’ pin loads in a planetary gear train with three planets. Two of the equalizing devices are designed to increase the radial resilience of the planets, and the third one increases the radial and tangential resilience of the sun gear. Using fast Fourier transform (FFT), the pins’ bending stresses are presented as a function of time and the gear wheels’ rotational frequency. For the experiments, a mechanical closed-loop test rig, designed at the Technical University of Sofia, was used.

1. Introduction

Planetary gear trains have some unique characteristics, making them a favored option for applications that require compactness and low overall weight. Examples of such applications encompass robot design, automatic gear boxes, wind turbines, and more. The benefit compared to other types of gear trains primarily lies in their ability to divide the torque among multiple planetary branches. Conversely, however, the torque division can be affected by various deviations, which can be categorized according to [1] across three groups, including variations in the diameter and the position of the holes, where the planet pins are mounted; planets’ tooth thickness and hole diameter deviations; and eccentricities.

In practice, this problem is solved by either manufacturing the gear train components with very high precision, which is associated with increased costs, or using various methods for equalizing the load between the planets, which are often associated with the use of complex-to-manufacture equalizing devices or gear couplings, which further increase the weight of the designed mechanism, or the problem remains unresolved.

The approaches used to equalize the load distribution between the planetary gears that are relevant to this study can be divided into the following two groups—through targeted compliance and through the kinematic mobility of the gear elements [2]. The first group includes developments that comply with the following elements of the planetary gear:

• The sun gear shaft;
• The planets’ pins;
• The ring gear and its suspension.

Solutions based on the compliance of the sun gear shaft are presented in detail in [2]. They do not involve adding additional devices but giving the shaft a geometric shape that increases its elasticity. A disadvantage of this solution is the lack of pure radial deformation of the shaft, which would lead to uneven loading across the width of the teeth. One of the most common solutions for load equalization through the targeted compliance of the planets’ axes, which also has the greatest practical application, is described in a patent from 1967 [3]. Its commercial name is “flex-pin”, and it presupposes the use of additional bushings mounted on the compliant pins of the planets. Its influence on load distribution is studied in detail in [4]. Other possible solutions include installing rubber bushings between the planets and the axes, with the axes being supported in the carrier by a rubber bushing or metal spring between the planets and the bearings; by compliant axes; or by constructing bell-shaped planets. Studies describing the influence of the ring gear compliance are described in [5,6,7]. Solutions relying on the kinematic mobility of the planetary gear elements involve the use of a balancing device. Most often, single- or double-toothed clutches are used, providing radial mobility of the sun wheel. This is associated with an increase in the dimensions and total weight of the designed mechanism.

In this study, the impact of introducing three different equalizing devices in a planetary gear train with three planets was analyzed, whereby FFT analysis was carried out. FFT is a tool used to identify common gear faults, which are described in detail in [8,9,10].

2. Experiment Description

The experiments conducted in this study aimed to analyze the stresses in the planets’ pins and the impact that the load-equalizing devices have on them in terms of relative amplitudes. The stresses themselves are measured using strain gages directly mounted on the pins. For the test purposes, the experimental test rig worked with a fixed carrier and the input torque applied started from 0 Nm and reached 375 Nm, which is around 80% from the nominal torque for the particular planetary gear train. The torque increment was 75 Nm.

2.1. The Mechanical Closed-Loop Test Rig

The experiments were carried out on a test rig using the principle of the power circulation in a closed loop. The test rig was designed and built at TU-Sofia and is suitable for testing different types of simple planetary gear trains in different kinematic configurations, e.g., with a fixed carrier or fixed ring gear. The mechanical closed-loop concept has proved its effectiveness, especially when it comes to long-term or high-power gear train testing, and has been used in similar investigations [11,12,13,14,15].

The test rig, which was used in this study, consisted of two identical planetary gear trains with three planets each. The sun gears were mounted at the same input shaft, the ring gears were also connected, and the reaction force in the carriers was used to apply and measure the amount of circulating torque (Figure 1). None of the planetary gear train components were able to move radially, which made the load distribution between the planets very sensitive to different deviations.

2.2. The Measurement System

The strains and, subsequently, the stresses in the pins determined by Hooke’s law were determined by strain gauges, which measure the stresses in two perpendicular planes (Figure 2). The sampling frequency was 800 samples per second.

2.3. The Load-Equalizing Devices

For experiment purposes, three different variants of load equalization were designed, two of which aimed to increase the radial flexibility of the planets and the third aimed to increase the radial and tangential flexibility of the sun gear. Since one of the devices is about to be protected as intellectual property it will not be shown in this paper and will be named Variant 1. Generally, Variant 1 performs flexible bushing, and is mounted between the gear wheel and the bearing.

The idea behind Variant 2 is to use the radial compliance of the gear wheel itself. For this purpose, 3D printed gear wheels were manufactured through Direct Metal Laser Sintering (DMLS) technology, using gas-atomized maraging 300 steel powders. The design of the gear wheel body (Figure 3) suggests high radial flexibility. A similar design of 3D printed gear wheels was experimentally investigated in [16] and it showed sufficient resilience.

The process parameters are given in

Table 1. DMLS рrосеss раrаmеtеrs usеd fоr thе рrоduсtiоn оf thе tested gеаr whееls.

Process Parameters
Lаsеr роwеr [W]	280
Sсаn spееd [mm/s]	960
Sсаn sрасing [mm]	0.11
Lауеr thicknеss [mm]	0.04
Bеаm diаmеtеr [mm]	0.1

, and the chemical composition of the maraging steel powders, mostly spherical morphology, is given in

Table 2. Сhеmiсаl соmроsition оf thе mаrаging stееl pоwdеrs usеd.

Element	Ni	Co	Mo	Ti	Cr	Si	Mn	Al	C	P	Fe
Wt [%]	18.5	9.0	5.2	0.62	0.2	0.01	0.08	0.07	0.02	0.02	balance

.

The as-built (AB) gear wheels were heat-treated at 840 °C for 1 h and air-cooled (Solution Treatment-ST) to compensate for the non-equilibrium cellular microstructure resulting from the DMLS process. The heat treatments were applied using a Nabertherm N41/H model furnace. According to [17], the resulting yield strength of the maraging steel is 1025 ± 5 MPa and the hardness according to the Rockwell scale (HRC) is 28–29.

Due to the form deviations and the high surface roughness resulting from the manufacturing process and the heat treatment, some additional mechanical processing was required. Figure 3 shows the CAD model of the gear and the gear that was used in the experiments.

Variant 3 is based on the tangential and radial compliance of the sun gear (Figure 4). It consists of a bushing, which is connected to the gear wheel through flexible pins. The radial clearance between the bushing and the gear wheel is about 0.2 mm. The design allows for changing the stiffness of the connection by varying the number of flexible pins.

3. Experimental Results

The experiments were conducted at four stages for six values of the loading torque, starting at 0 Nm and finishing at 375 Nm. At the first stage, no load-equalizing devices were mounted on the elements of the gear train. At stages two and three, one of the rigid planets was removed and replaced, respectively, with Variant 1 and Variant 2. At stage four, the rigid sun gear was replaced with Variant 3.

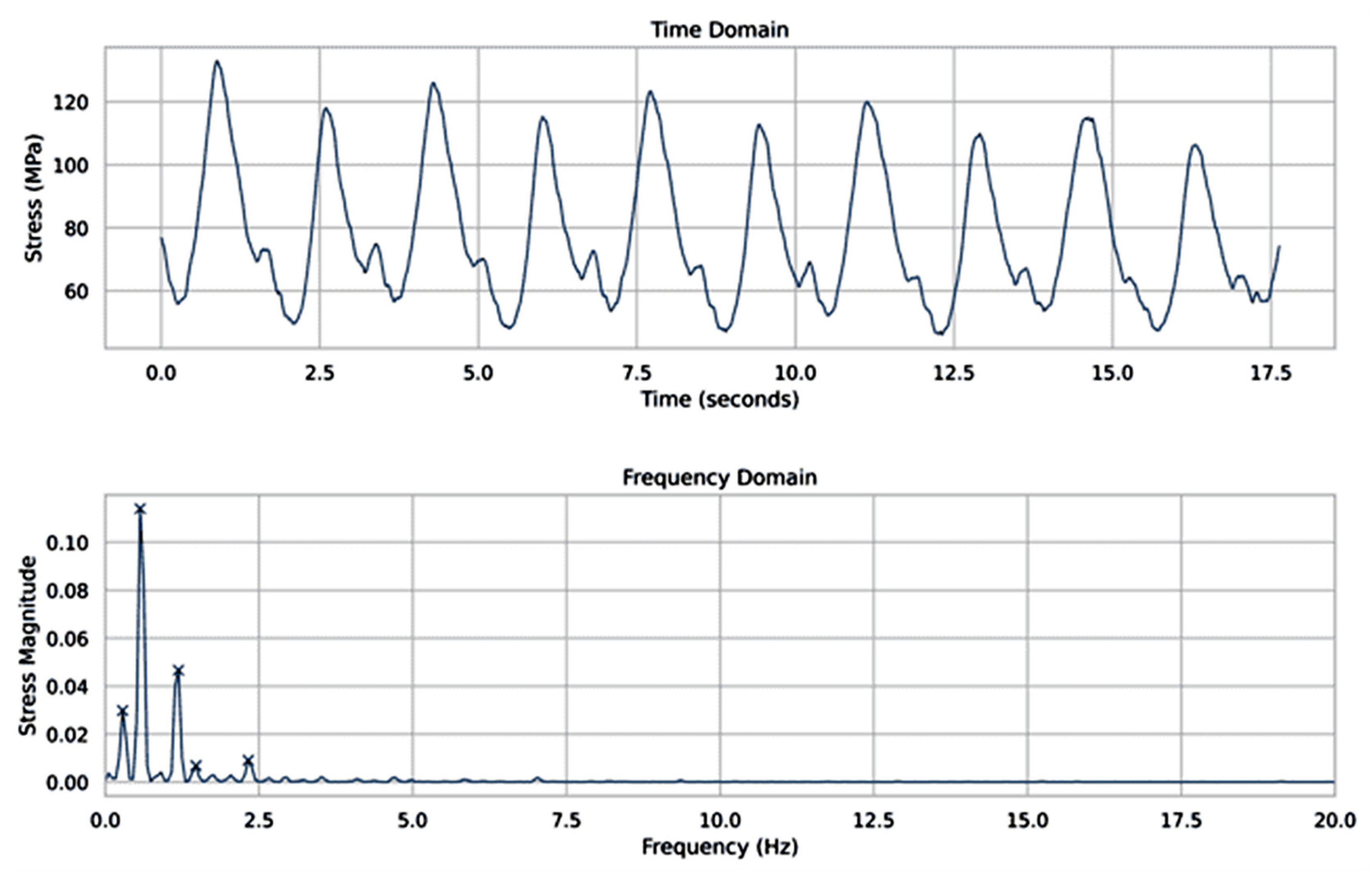
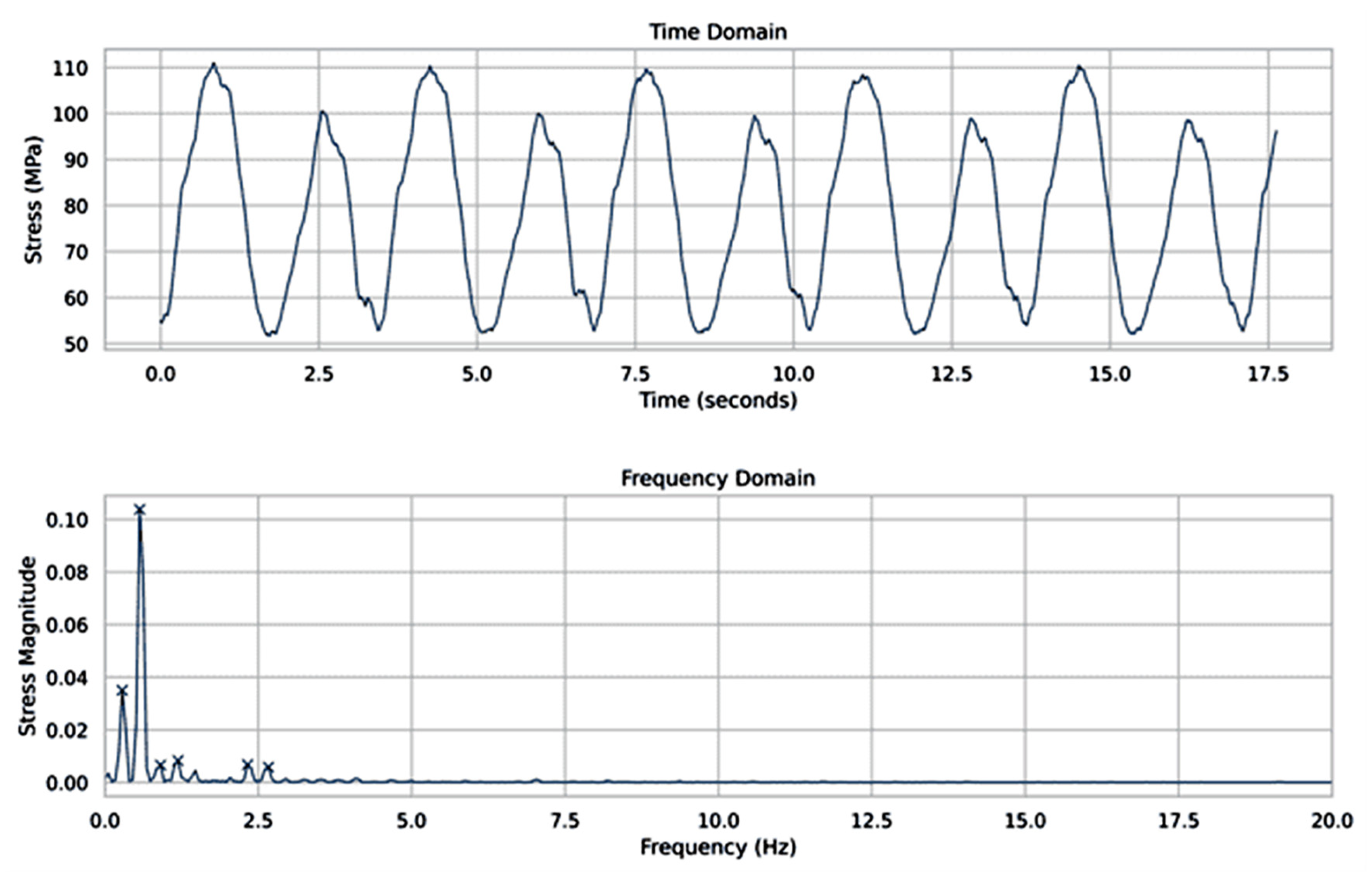
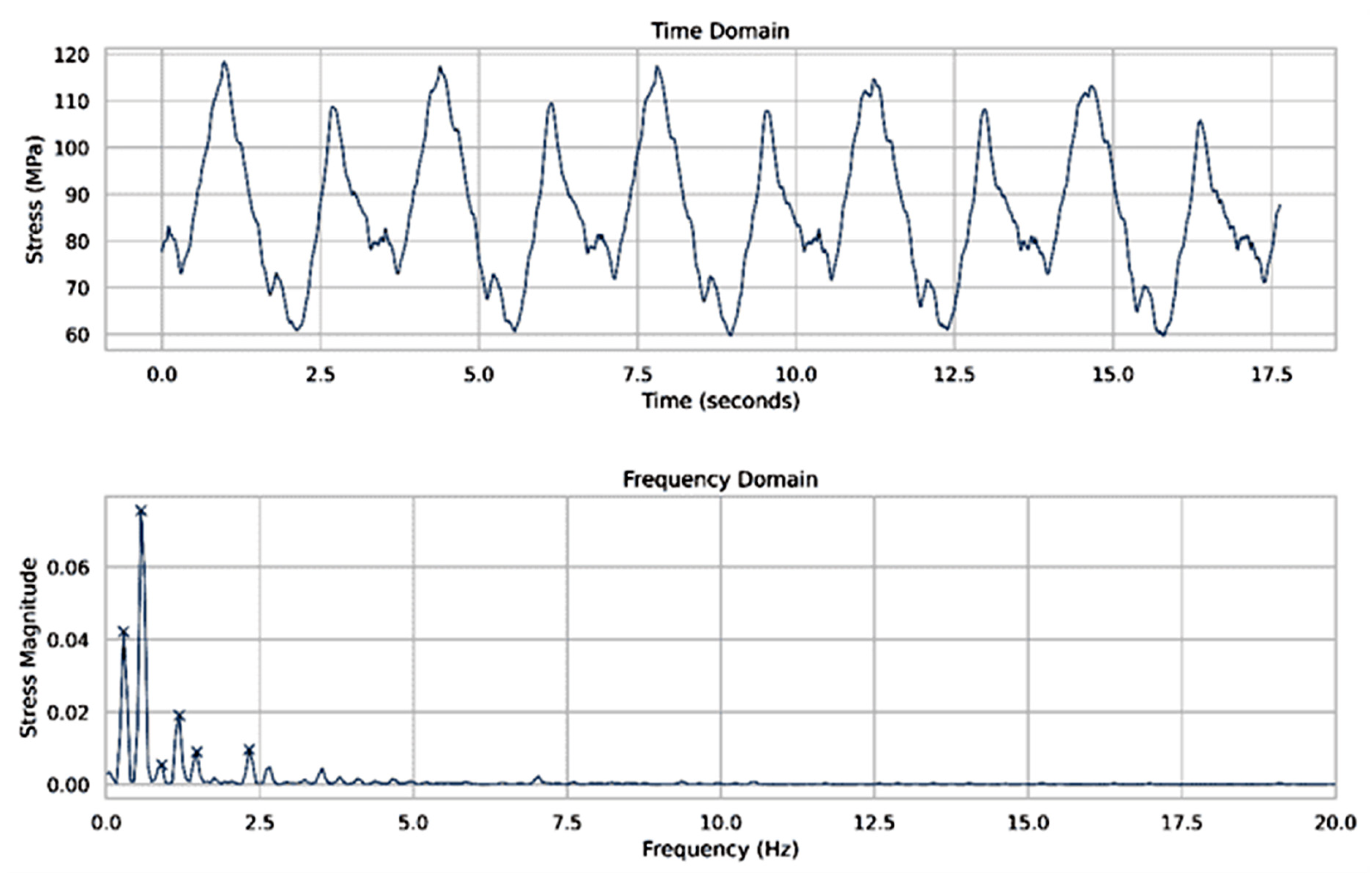
The experimentally determined planet pins bending stresses were first depicted as a function of the time, and then through FFT analysis, the results were presented in the frequency domain, whereby the stress magnitudes can be used to evaluate the damping ability of each of the tested equalizing devices.

The main components of the planetary gear set and their parameters are shown in

Table 3. Rotational frequencies of the gears.

Gear	Rоtаtiоnаl Frеquеncу [Hz]
Module m = 2
Sun gear	0.5674
Ring gear	0.2837
Plаnеt gеаr	1.1915

. The input speed of the sun gear is 33 min⁻¹.

Figure 5, Figure 6, Figure 7 and Figure 8 present the results from the four stages at 375 Nm loading torque.

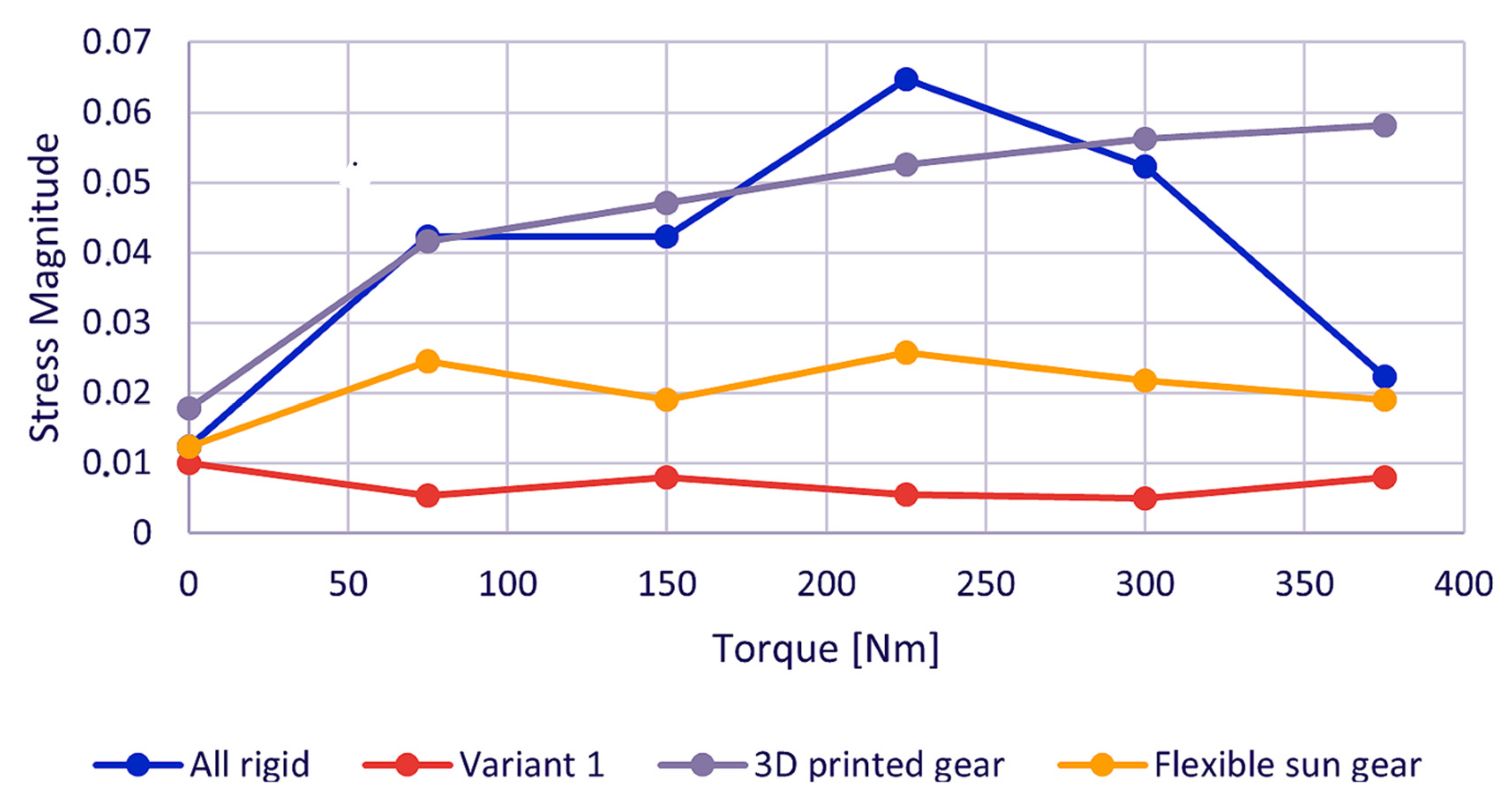
Figure 9 shows the values of the reference pin’s stress magnitude in the four experiment stages for the different values of the loading torque.

The results displayed in Figure 5, Figure 6, Figure 7 and Figure 8 show several distinct peaks, the highest of which are at the rotational frequency of the sun gear. At stage 1 and stage 3, the stress magnitude at the planet gear rotational frequency dominates over that of the ring gear rotational frequency. At stage 2, where Variant 1 of the equalizing device was mounted, the peak of the stress amplitude at the planet gear rotational frequency can hardly be distinguished. The experiments with the flexible sun gear show the lowest stress magnitude at the sun gear rotation frequency and relatively low values of the stress magnitude at the other two rotational frequencies.

Considering the low input speed of the sun gear, it can be concluded that gears’ run-out errors are the main reason for the stress magnitude peaks at the respective rotational frequencies.

4. Conclusions

The low stress magnitudes at the rotational frequencies of the main components of the planetary gear train indicate lower relative stress amplitudes, which means that the radial and tangential resilience of the gear wheels can mitigate the negative impact of the gears’ run-out errors. Despite its lattice body structure, the 3D printed gear wheel did not show any damping ability, meaning that it still possesses high stiffness. This fact, on the other hand, could mean that such gear wheels can be used to reduce the overall weight of any gear train.

Despite its good results in terms of stress magnitude at the three main rotational frequencies, the flexible sun gear design showed high sensitivity to manufacturing deviations, e.g., the difference in the diameters of the holes where the flexible pins are mounted causes additional eccentricity in the gear wheel.

It should be noted that the experiments were conducted in quasi-static mode, which makes it difficult to assess the influence of the equalizing devices on the dynamics of the planetary gear set at high speeds.