Resilience of UNet-Based Models Under Adversarial Conditions in Medical Image Segmentation ^†

Abstract

Adversarial modifications of input data can degrade the stability of deep neural networks in medical image segmentation. This study evaluates the robustness of UNet and Att-UNet++ architectures using the NuInsSeg dataset with annotated nuclear regions from various tissue sources. Both models were trained and tested under eight perturbation types, including gradient-based, iterative, and stochastic methods, with identical parameter settings. In the absence of distortions, Att-UNet++ produced higher segmentation results with a Dice of 0.7160 and a mean IoU of 0.6190 compared to 0.6424 and 0.4732 for UNet. Under NI-FGSM and Gaussian noise, Att-UNet++ experienced a greater reduction in mean IoU, reaching 0.1215 and 0.0658, while UNet maintained 0.1968 and 0.2329. Loss landscape analysis showed smoother surfaces for Att-UNet++, yet revealed increased responsiveness to directional gradients. The findings suggest that improvements in segmentation accuracy through architectural modifications may be accompanied by increased vulnerability to input changes, highlighting the necessity of robustness evaluation in model development for medical image analysis.

1. Introduction

Medical image interpretation constitutes a central role in modern clinical workflows. It provides physicians with an efficient tool to diagnose and monitor the progression of various diseases [1]. Computational medical image processing includes steps such as image acquisition, enhancement, analysis, and segmentation [2]. With the introduction of deep learning (DL) approaches, these processes are becoming increasingly automated to extract complex features from different modalities [3]. Among these applications, medical image segmentation is extremely important to distinguish anatomical structures. However, the segmentation of medical images, particularly at the cellular and skin lesion level, remains challenging due to irregular structures and overlapping regions [4]. Another fundamental task is medical image classification, which aims to assign diagnostic labels to entire images and is widely used for disease detection [5]. In contrast to traditional image processing techniques, which rely on manual feature creation and explicit rule-based operations, deep learning (DL) methods derive hierarchical representations directly from the raw data through optimization [6]. This difference shifts the focus from manual feature extraction to data-driven model training, changing the approach to solving image analysis challenges. Convolutional neural networks (CNNs) have emerged as a foundational DL architecture in medical image analysis as it is capable of capturing patterns using convolutional operations [7]. Fully convolutional networks (FCNs), as well as models based on models that include U-Net and its variants, are often used to solve these problems due to their encoder and decoder design that preserves spatial resolution across the network [8,9]. Transfer learning [10] facilitates the adaptation of CNNs to novel medical imaging tasks by leveraging previously learned parameters from related domains, thereby reducing the reliance on large annotated datasets to a minimum [11]. Even slight changes in the input medical images could mislead the segmentation models, leading to confidently incorrect extraction of anatomical or pathological regions, such as missing tumor boundaries. Among the state-of-the-art (SOTA) approaches, a method using a cascaded autoencoder architecture with modified adaptive instance normalization stands out, which allows the modification of image feature statistics in order to create realistic images [12]. Another recent method, Mb-AdA [13], uses orthogonal image moments to remove information subtly without adding noise, thereby misleading classification and segmentation models while preserving the structural integrity of medical images. Furthermore, in another study of full and partial adversary attacks, such as FGSM and PGD, applied in different spatial domains, it was shown that even localized distortions might reduce the stability of the model by targeting salient areas [14]. Despite the overall influence of different attack strategies on DL-based medical image analysis, it remains understudied, especially in terms of their generalizability to different imaging.

This study establishes a systematic assessment paradigm for quantifying the resilience of UNet-based architectures by exposing them to various gradient, iterative, and stochastic perturbation algorithms under uniform experimental conditions, while utilizing loss landscape analysis as an auxiliary tool to determine model sensitivity.

2. Materials and Methods

The methodology incorporated the NuInsSeg dataset [15] for nuclear segmentation in histological specimens. The dataset comprises 665 image patches of 512 × 512 pixels, subsequently processed to 256 × 256 dimensions, containing around 30,700 annotated nuclei derived from 31 distinct human and murine organs. Data augmentation procedures expanded the training corpus to 1000 samples. Dataset partitioning followed an 80:10:10 ratio, yielding 800 training, 99 validation, and 66 test images.

This investigation evaluated two CNN architectures for nuclear segmentation on the NuInsSeg dataset UNet [16] and Att-UNet++ [17]. UNet implements a symmetric encoder–decoder structure with four stages comprising dual convolutional layers with ReLU activations and respective downsampling or upsampling operations. Att-UNet++ features a densely connected nested [18] architecture across five resolution scales, integrating attention gates at skip connections [19]. Both architectures underwent comparative analysis under adversarial changes.

The visual illustrations of the input sample, the applied perturbation and the resulting image after distortion are shown in Figure 1.

These distortions, when applied to the original image, create a subtly modified version designed to mislead the segmentation model. This research evaluated the resilience of segmentation models to eight types of attacks, including gradient, iterative, and noise exposures.

The fast gradient sign method (FGSM) [20] is a strategy for generating adversarial samples in which a distortion in the direction of the sign of the loss function gradient is added to the original image X distortion in the direction of the sign of the gradient:

$$\tilde{X}=X+\epsilon \cdot sign({\nabla }_{X}l(X,y_{\mathit{target}})),$$

(1)

where $\tilde{X}$ is an adversely perturbed input, X is the original image, and $\epsilon$ controls the perturbation magnitude, ${\nabla }_{X}l(X,y)$ [21].

Projected gradient descent (PGD) is a method [22] for generating adversarial examples based on the gradient lifting of the loss function with a projection of the result back into the allowable space.

Momentum iterative FGSM (MI-FGSM) is a gradient-based unfavorable perturbation method in which the perturbation vector is computed by recursively integrating the information over several iterations [23]. The algorithm differs from standard iterative approaches by including a momentum term that maintains the current average gradient directions:

$$g^{(t+1)}=\mu \cdot g^{(t)}+{{\displaystyle \frac{{\nabla }_{x}J(x^{(t)},y)}{‖{\nabla }_{x}J(x^{(t)},y)‖}}}_1,$$

(2)

where x^(t) is the current perturbed image at iteration t, $\alpha$ is the update step size, $\mu$ is the momentum decay factor, $J(x,y)$ is the loss function, and ${\nabla }_{x}j(x,y)$ is the gradient of the loss.

TI-FGSM (translation-invariant FGSM) is a method for generating bias-resistant attack examples [24]. Unlike classical methods, TI-FGSM considers not only the original image but also its shifts along the spatial axes, aggregating the gradients from these translations.

$$\tilde{X}=\arg \underset{z\in {\beta }_{\infty }(x)}{\max }{\displaystyle \sum _{m,n}{w}_{mn}\cdot l({\tau }_{mn}(z),c)},$$

(3)

where $\tilde{X}$ is the final adversarial image, z is an intermediate perturbed image, x is the original clean input, ${\tau }_{mn}$ is the translation operation shifting the image, $w_{mn}$ is the weight assigned to each translation, l is the loss function, and ${\beta }_{\infty }(x)$ denotes the ball of permissible deviations with radius ϵ around x.

Diverse FGSM (DIFGSM) is an extension of FGSM that also improves the tolerance of unfavorable examples by applying random transformations to the input data before computing the gradients. DI-FGSM introduces stochastic transformations of the input data at each iteration of the gradient computation to generate more diverse external changes.

$$x_{k+1}={\mathrm{Pr}}_{\delta }\left\{z_k+\eta \cdot sign({\nabla }_{u}l(R(z_k),c))\right\},$$

(4)

where x_k+1 is the adversarial example at iteration k, $\eta$ is the update step size, R is the random transformation applied to the input, and ${\mathrm{Pr}}_{\delta }$ is the projection onto the $l_{\infty }$ ball of radius $\delta$.

Scale-invariant and diverse input FGSM (SI-DI-FGSM) is an advanced attack strategy that increases the tolerance of changes by combining two mechanisms: scale-invariant gradient [25] computation and diverse input transformation. The scale-invariant component generates unfavorable gradients by averaging the loss gradients over multiple modified versions of the input image, which reduces sensitivity to the scale of the input.

Nesterov iterative FGSM (NI-FGSM) is a gradient-based adversarial strategy that complements the traditional iterative FGSM system by integrating Nesterov’s momentum mechanism to improve transferability by computing gradients at look-ahead point updates [26].

Gaussian noise (GN) perturbation represents a non-adversarial robustness assessment methodology characterized by the superimposition of stochastic additive disturbances sampled from a normal distribution with zero mean and predetermined variance onto the input signal.

$$\tilde{x}=x+\in , \in \sim N(0,{\sigma }^2),$$

(5)

where $x$ denotes the clean input, $\tilde{x}$ represents the noise-perturbed image, $\in$ is the additive Gaussian noise, $N(0,{\sigma }^2)$ defines a normal distribution with mean 0 and variance ${\sigma }^2$, and $\sigma$ controls the magnitude of the noise.

All adversarial attacks were conducted at the same settings to ensure a valid comparison. The epsilon perturbation value was fixed at 0.03, the alpha step size was fixed at 0.005, and the number of iterations was fixed at ten for all iterative methods. For the moment-based attacks, a fading factor of 1.0 or 1.5 was used. The DI-FGSM attack used stochastic transformations with a probability of 0.7. The GN method introduced additive variations with a standard deviation of 0.1.

In this research, the behavior of segmentation models was assessed through quantitative analysis using established performance indicators. These include the Dice coefficient, mean intersection over union (mean IoU), accuracy, and Dice loss [27].

The Dice coefficient reflects the degree of spatial correspondence between the predicted (P) segmentation domain and the real annotation (G), which serves as a measure of topological correspondence.

$$\mathit{Dice} \mathit{coefficient}={\displaystyle \frac{2\cdot \left|P\cap G\right|}{\left|P\right|+\left|G\right|}}$$

(6)

Mean IoU estimates the average overlap across all classes, offering a balanced metric.

$$Mean IOU={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\frac{\left|P_i\cap G_i\right|}{P_i\cup G_i}}$$

(7)

Accuracy defines the fraction of identified pixels with respect to the full set of image pixels [28]. Dice loss [29] is determined by the Dice coefficient and serves the purpose of optimization by penalizing for poor agreement between predicted and actual segmentations during model training.

The experimental setup used was an NVIDIA A100 GPU. The software environment included Python 3.10 and TensorFlow 2.13.0.

3. Results

In this study, a dataset comprising 532 annotated medical images was employed. Two segmentation models, UNet and Attention-UNet++, were trained using a mini-batch size of 8 for 60 epochs. A comparative assessment of the segmentation efficiency of the models under consideration is summarized in

Table 1. Comparative analysis of segmentation performance based on validation metrics.

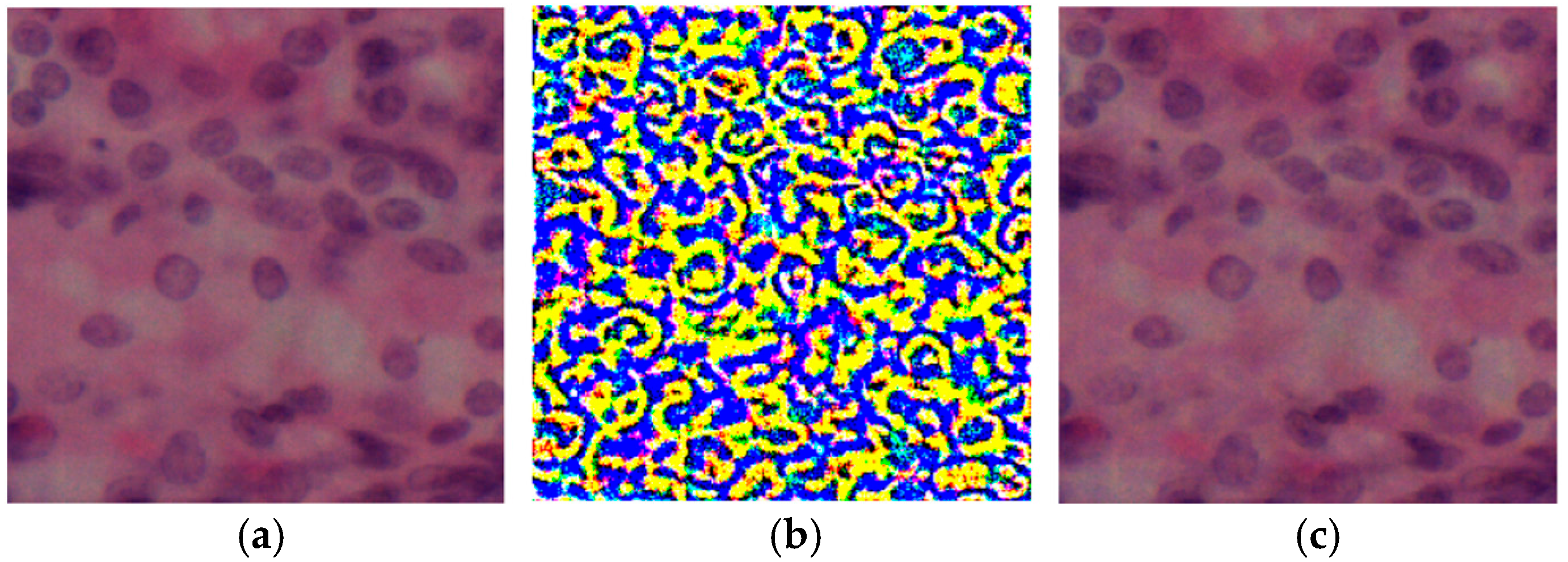
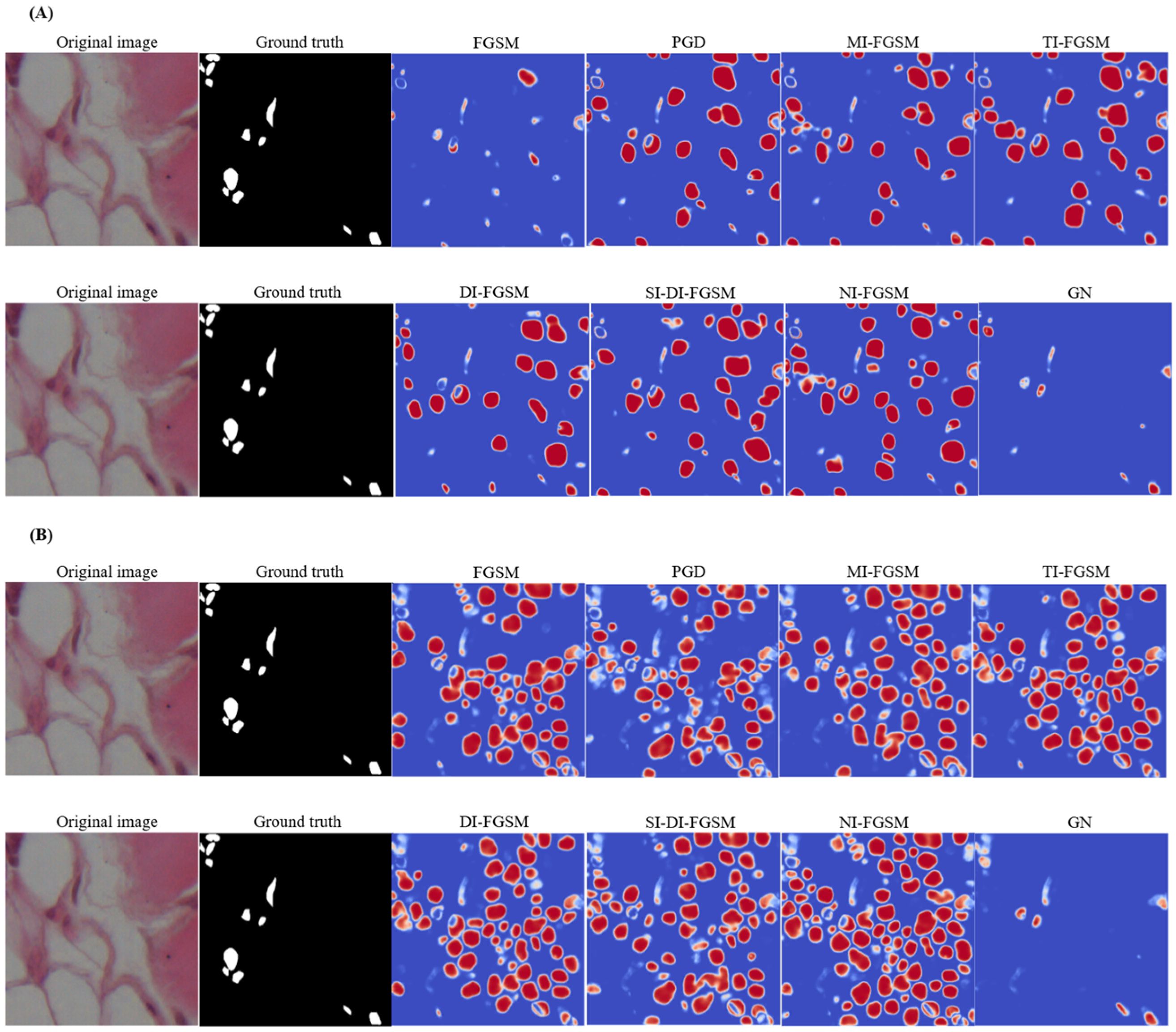
Metrics	UNet	Att-Unet++
Dice	0.6424	0.7160
Mean IOU	0.4732	0.6190
Accuracy	0.9009	0.9292

.

As summarized in Table 1, the performance of the Att-Unet++ model exceeds that of UNet in all metrics considered. The Dice metric for Att-Unet++ is 0.7160 compared to 0.6424 for UNet, indicating an increase of about 11.46%. Average IOU improves from 0.4732 to 0.6190, representing a relative increase of 30.77 percent. Accuracy improves from 0.9009 to 0.9292, corresponding to an improvement of 3.14 percent. The quantitative evaluation of model efficiency was conducted using the Dice similarity metric calculated on a subset of scores with retention, and detailed comparative results are presented in

Table 2. Dice coefficient of segmentation models under adversarial and noise-based attacks on the test set.

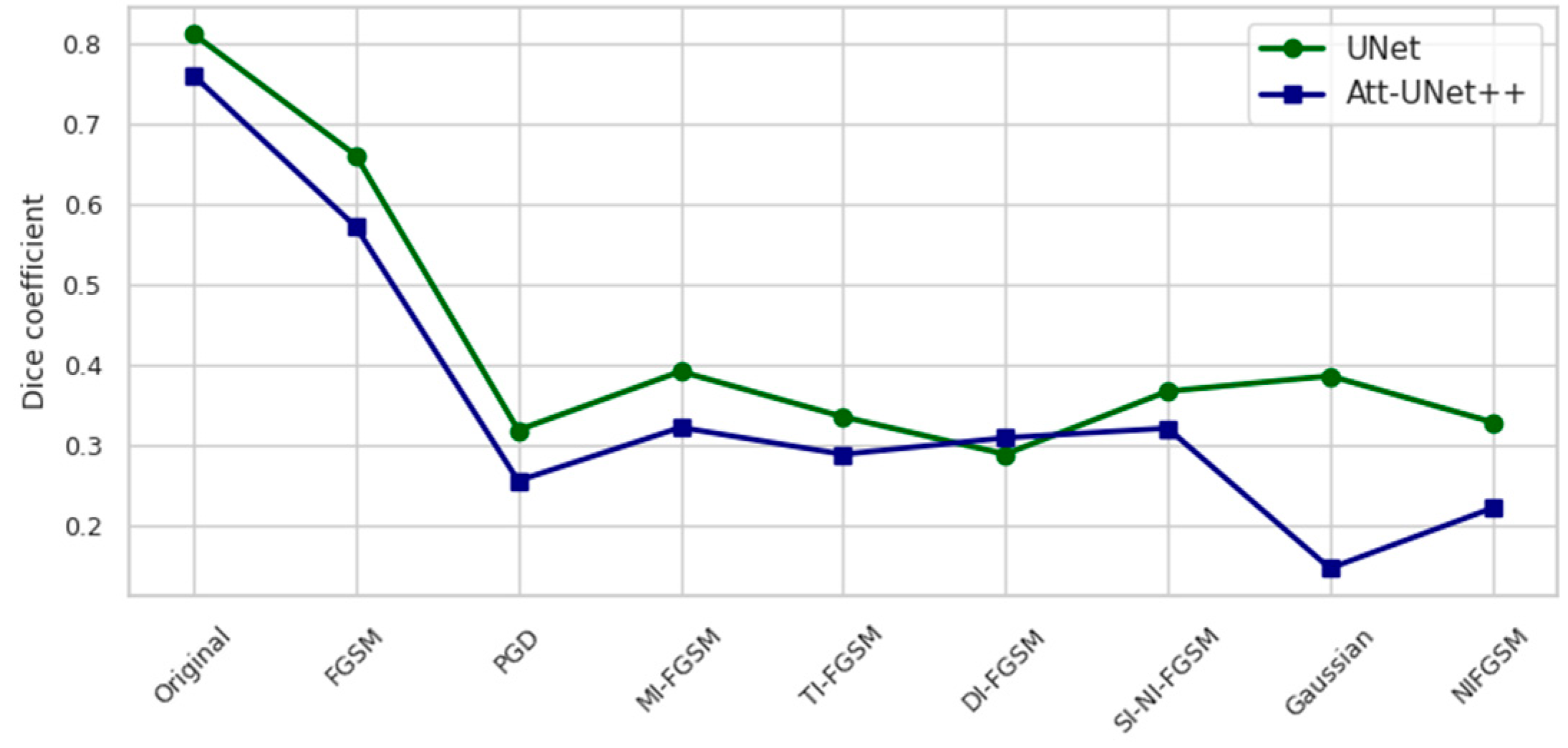
Attack	UNet	Att-Unet++
Original image	0.8118	0.7603
FGSM	0.6607	0.5717
PGD	0.3185	0.2553
MI-FGSM	0.3185	0.3217
TI-FGSM	0.3350	0.2882
DI-FGSM	0.2884	0.3088
SI-DI-FGSM	0.3667	0.3208
NI-FGSM	0.3859	0.2212
GN	0.3284	0.1463

.

On baseline, undisturbed test images, Att-Unet++ shows a 6.34% reduction in Dice performance compared to UNet, indicating a slightly less optimal baseline generalization. Under gradient attacks such as FGSM, PGD. and TI-FGSM, Att-Unet++ demonstrates a further reduction from 13% to 20%, confirming a higher sensitivity to directional changes. Notably, Att-Unet++ achieves marginal improvements with MI-FGSM and DI-FGSM, with respective relative increases of 1.00% and 7.08%, indicating limited robustness in the presence of pulse and input diversity. However, the performance with NI-FGSM and GN deteriorates considerably, with Dice scores decreasing by 42.66% and 55.45%, respectively. The comparative performance of segmentation models based on mean IOU under different adverse distortions is systematically presented in

Table 3. Mean IOU of segmentation models under adversarial and noise-based attacks on the test set.

Attack	UNet	Att-Unet++
Original	0.6845	0.6550
FGSM	0.4899	0.4153
PGD	0.1893	0.1428
MI-FGSM	0.2441	0.1896
TI-FGSM	0.2003	0.1690
DI-FGSM	0.1674	0.1788
SI-DI-FGSM	0.2246	0.1899
NI-FGSM	0.1968	0.1215
GN	0.2329	0.0658

.

In the baseline analysis, Att-Unet++ exhibits a slightly lower average IOU compared to UNet, with a relative decrease of 4.31 percent. When exposed to hostile perturbations, the degree of performance degradation differs by attack type. Moderate degradation is observed for FGSM and TI-FGSM attacks, resulting in 15.21 and 15.62 percent performance degradation, respectively. A more severe degradation is observed for iterative attacks such as PGD and NI-FGSM, where the average IOU drops by 24.58 and 38.27 percent, respectively. The introduction of GN leads to the most pronounced decrease, with the average IOU for Att-Unet++ dropping to 0.0658, which corresponds to a 71.73 percent decrease compared to UNet. Interestingly, under DI-FGSM conditions, Att-Unet++ shows a slight improvement over UNet by 6.82%, which may reflect the advantage of the attention mechanism in processing spatially transformed input data. The loss values obtained under adversarial and noise-based test-time conditions for both segmentation models are shown in

Table 4. Comparative loss values for segmentation under synthetic distortions.

Attack	UNet	Att-Unet++
Original	0.3408	0.2127
FGSM	1.0201	0.6375
PGD	3.7275	2.3940
MI-FGSM	2.5136	1.4659
TI-FGSM	3.4177	2.0134
DI-FGSM	3.4365	1.9829
SI-DI-FGSM	3.1738	1.9152
NI-FGSM	4.0243	2.6552
GN	2.0101	1.5234

.

Under baseline conditions, the loss value for Att-Unet++ is 37.6 percent lower compared to UNet. Across all attack types, Att-Unet++ consistently demonstrates lower loss values. The most substantial reductions are observed under PGD and NI-FGSM attacks, with decreases of 35.76 percent and 33.99 percent, respectively. Moderate improvements are noted under MI-FGSM and TI-FGSM, with reductions of 41.70 percent and 41.09 percent. The smallest difference is found under Gaussian noise, where the loss decreases by 24.21 percent. These findings highlight the enhanced robustness of Att-Unet++ over UNet, particularly under gradient-based adversarial conditions.

Following the quantitative results presented in the previous tables, Figure 2 illustrates the trends in model validation performance during training (Figure 2).

The validation dynamics presented in Figure 3 reveal that Att-Unet++ consistently outperforms UNet in both Dice and average IOU across all training epochs. Att-Unet++ reaches a peak Dice around epoch 50 and maintains stable performance thereafter, while UNet reaches a lower plateau earlier. Similarly, the average IOU for Att-Unet++ increases dramatically and stabilizes around epoch 30, outperforming UNet, which exhibits slower convergence.

A comparative graphical representation of the model behavior under attack and noise conditions is presented in Figure 3 and Figure 4. Figure 3 represents the Dice coefficient performance responses, while Figure 4 depicts the corresponding loss values.

Figure 3 illustrates the Dice coefficient performance of UNet and Att-Unet++ models under a range of adversarial and noise-based attack conditions on the test set. In the clean setting, UNet outperformed Att-Unet++ by 6.8%. Both models exhibited substantial performance degradation when subjected to gradient-based deviations, with PGD and NI-FGSM attacks causing the most significant drops. UNet’s Dice coefficient decreased by 60.8% and 52.5% under PGD and NI-FGSM, respectively, whereas Att-Unet++ declined by 66.4% and 70.9% under the same conditions. Exposure to GN resulted in a 59.5% reduction for UNet and 80.8% for Att-Unet++. Across all distortions, UNet consistently maintained higher Dice scores.

Figure 4 presents the loss values of UNet and Att-Unet++ under various attack conditions. UNet demonstrates higher sensitivity, with loss increasing by 991.1% under PGD and 1079.6% under NI-FGSM. In contrast, Att-Unet++ shows comparatively lower increases of 1024.2% and 1147.2% under the same attacks. Across all scenarios, Att-Unet++ consistently maintains lower loss.

Under PGD, the Dice coefficient of UNet decreases by 60.77 percent and that of Att-Unet++ by 66.43 percent. NI-FGSM results in a Dice reduction of 52.45 percent for UNet and 70.91 percent for Att-Unet++. Corresponding loss increases are observed: for PGD, the rise is 993.86 percent in UNet and 1024.89 percent in Att-Unet++, while for NI-FGSM, the increases reach 1079.98 percent and 1148.24 percent, respectively.

The local behavior of the loss function near adversarial noise was investigated using 3D surface visualization. Figure 5 depicts the loss landscapes for Att-UNet++ and UNet under NIFGSM distortions along the main adversarial and orthogonal directions.

Figure 5 illustrates the loss landscapes of the segmentation models Att-UNet++ (a) and UNet (b) under deviations generated by the NIFGSM method. The x-axis corresponds to the perturbation along the adversarial direction ε₁, while the y-axis denotes the orthogonal direction ε₂. The loss values are encoded using a perceptually uniform colormap. The surface in subplot (a) reveals a smooth and monotonic increase in loss for Att-UNet++, with the maximum value reaching approximately 2.25 at ε₁ = 0.02 and ε₂ = 0.02. In contrast, the surface for UNet in subplot (b) is characterized by irregular elevations and sharper gradients. The peak loss reaches around 2.0 but occurs across a more fluctuating region.

The Att-UNet++ loss surface exhibits higher regularity and reduced gradient dispersion in ε-space, implying increased robustness to local perturbation biases. The UNet topology has sharper discontinuities and increased curvature, which potentially indicates greater susceptibility to hostile gradient fluctuations. This divergence in loss landscape geometry suggests that Att-UNet++ maintains a more stable optimization trajectory under adverse conditions, whereas irregularities in the UNet surface may contribute to gradient bias. Figure 6 displays the effect of the different attacks.

Among PGD attacks, MI-FGSM, MI-FGSM, TI-FGSM, SI-DI-FGSM, and NI-FGSM cause substantial degradations, leading to widespread segmentation errors, as evidenced by the prominent red and blue areas. DI-FGSM also exhibits notable sensitivity, especially when over-segmenting non-nuclear regions. In contrast, FGSM and GN have relatively minor effects on the model. The segmentation discrepancies resulting from different perturbations are examined in subfigure (A), where the pixel-level difference maps generated by the UNet model give an indication of the prediction shifts before and after the exposure of the attack. In comparison with (A), (B) illustrates identical changes applied to Att-UNet++, and the UNet architecture demonstrates increased vulnerability to adversarial noise. Difference maps reveal more extensive chromatic variations, indicating reduced segmentation stability under perturbation conditions. Iterative and momentum-based methods produce significant alterations to predicted segmentation masks. Under FGSM perturbation, UNet exhibits considerable deviation from baseline predictions, while Att-UNet++ maintains greater consistency.

4. Conclusions and Future Work

This study investigated the vulnerability of CNN architectures to unfavorable factors used for nuclei segmentation in histopathological images. The analysis was performed on the NuInsSeg dataset containing hematoxylin and eosin-stained nuclei from different tissues. Two models, UNet and Att-UNet++, were evaluated under eight types of distortions to assess robustness. Although Att-UNet++ showed better segmentation performance on undisturbed data, with a Dice coefficient of 0.7160 and IoU of 0.6190, it showed greater performance degradation under certain adversary attacks. Specifically, under NI-FGSM and Gaussian noise, the model’s average IoU decreased to 0.1215 and 0.0658, respectively. In comparison, UNet reached 0.1968 and 0.2329 under the same conditions. The loss landscape analysis also showed that Att-UNet++ retains a smoother topological profile but remains more sensitive to gradient perturbations. These results suggest that while architectural complexity can improve baseline performance, it can also create different vulnerability profiles. Nevertheless, the current scope of the study is limited to binary segmentation performed on a single bivariate dataset. Validation on different datasets was not performed, which limits the generalizability of the results obtained. Furthermore, the analysis was limited to two CNN architectures, excluding SOTA lightweight or transformer-based models. Prospective research will include comparative evaluations of different datasets and modalities. Furthermore, subsequent studies may investigate innovative defense strategies [30], including attention-driven noise regularization.