Modeling and Control of Permanent Magnet Generators with Fractional-Slot Concentrated Windings Working with Active Converters for Wind Power ^†

Abstract

This paper presents modeling for an external rotor permanent magnet generator (PMG) with fractional-slot concentrated windings working with a power electronic converter in the rotor magnetic field coordinate—the model is also called the DQ model. The model is needed to synthesize controllers of the PMG. Additionally, modeling for an active rectifier of the PMG is also investigated. The models of PMG and the active rectifier with two closed loops, namely the current loop and dc voltage loop, are verified by simulation in Matlab/Simulink. By modeling PMG in the rotor magnetic field coordinate, vector current can be decomposed in two independent currents, namely active current and reactive current. By controlling the active current, active power or electromagnetic torque or DC bus voltage can be controlled. By setting a relevant reactive current, the power factor or reactive power or rotor magnetic flux of PMG can be controlled. Simulation results of control PMG working with an active converter, such as pulse width modulation voltage, current, DC voltage, or power, are reported. The simulation helps to synthesize controllers and improve performances of the PMG working with the converter in wind applications.

1. Introduction

The d-q model is widely used for induction machines and permanent magnet (PM) machines with distributed windings. The d-q model of a PM machine is used as a prerequisite to design the controllers of an active converter (CVT) [1,2,3,4,5,6,7,8]. It is also commonly used for the fast simulation of the performance of a PM machine. Recently, it has been proven that the d-q model is reliable enough for studying voltage and torque performances of PM machines with concentrated windings. However, this type of PM generator (PMG) has less sinusoidal voltage and flux linkage than the one with distributed windings. This paper’s purpose is to comprehensively study the modeling of concentrated winding PM machines working with an active converter in both generator mode and motor mode to design controllers and improve the performance of the PM machine-converter system. In addition, we will develop a fundamental theory to explain the current model in both rotor magnetic field-oriented control (RFOC) and voltage-oriented control (VOC). Thanks to the mathematical model-based control, the current vector is decomposed into active and reactive currents, which are independently controlled. As a consequence, the voltage vector and current are unified and the power factor reaches 1. Therefore, generating power is utilized to the maximum and a minimum power loss is reached.

The stator coordinator is defined as having the α-axis identical to the winding phase a-axis of the natural coordinator a-b-c and the β-axis being perpendicular to the α-axis. Therefore, the stator coordinator is a standstill coordinator. The rotor magnetic field coordinator in the PMG model is defined as having the d-axis (in this case, reactive current) identical to the direction of the vector rotor magnetic field and the q-axis (in this case, active current) perpendicular to the d-axis. Therefore, the rotor field coordinator (RFC) is a rotating coordinator. In the steady state, the dq-coordinator synchronously rotates with the angle speed of the fundamental rotor magnetic field, so that electrical current components in the d and q directions are DC quantities. The RFC-based model of a PM machine is often used for motor control according to the rotor field-oriented control (FOC) method in the pitch drives of a wind turbine or grid-connected generator [9,10,11,12].

Conversely, for the modeling of a pulse width modulation (PWM) AC/DC converter according to the Voltage-Oriented Control (VOC) method, the d-axis (in this case, active current) is identical to the vector voltage, and the q-axis (in this case, reactive current) is perpendicular to the d-axis. Therefore, by controlling the active current, the DC voltage can be controlled, and by controlling the reactive current, the power factor or reactive power can be controlled. The VOC is utilized to control the inverter of the grid side and the electrical generator in the case of generator standing alone.

This paper is organized as follows. Firstly, the d-q models of both PMG and CVT at different coordinates are developed to design controllers and explain the PM machine’s performances and the operating modes, such as maximum torque in motor mode and active and reactive power control in generator mode. Then, the models are simulated in Simulink/Matlab^®. Finally, simulation results are used to study performances of the PM machine working with the PWM active rectifier.

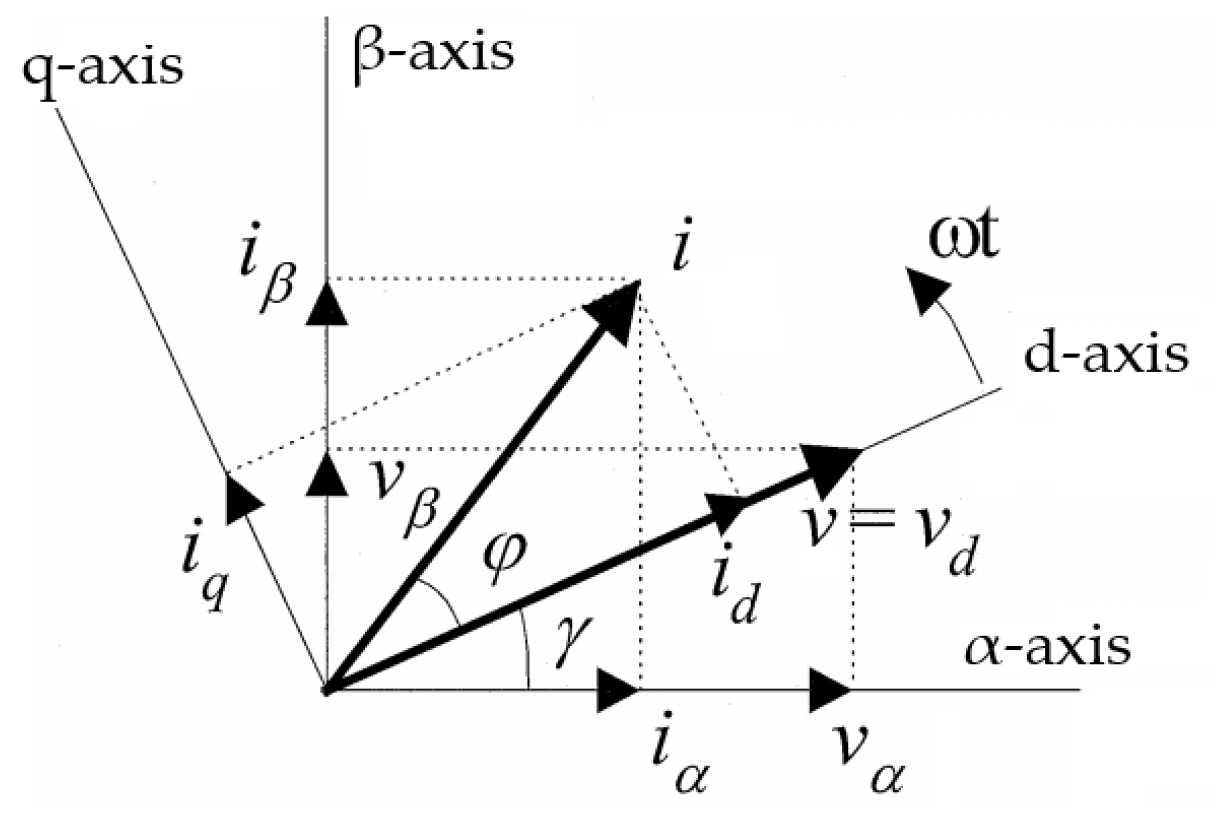
2. The d-q Model of the PM Machine

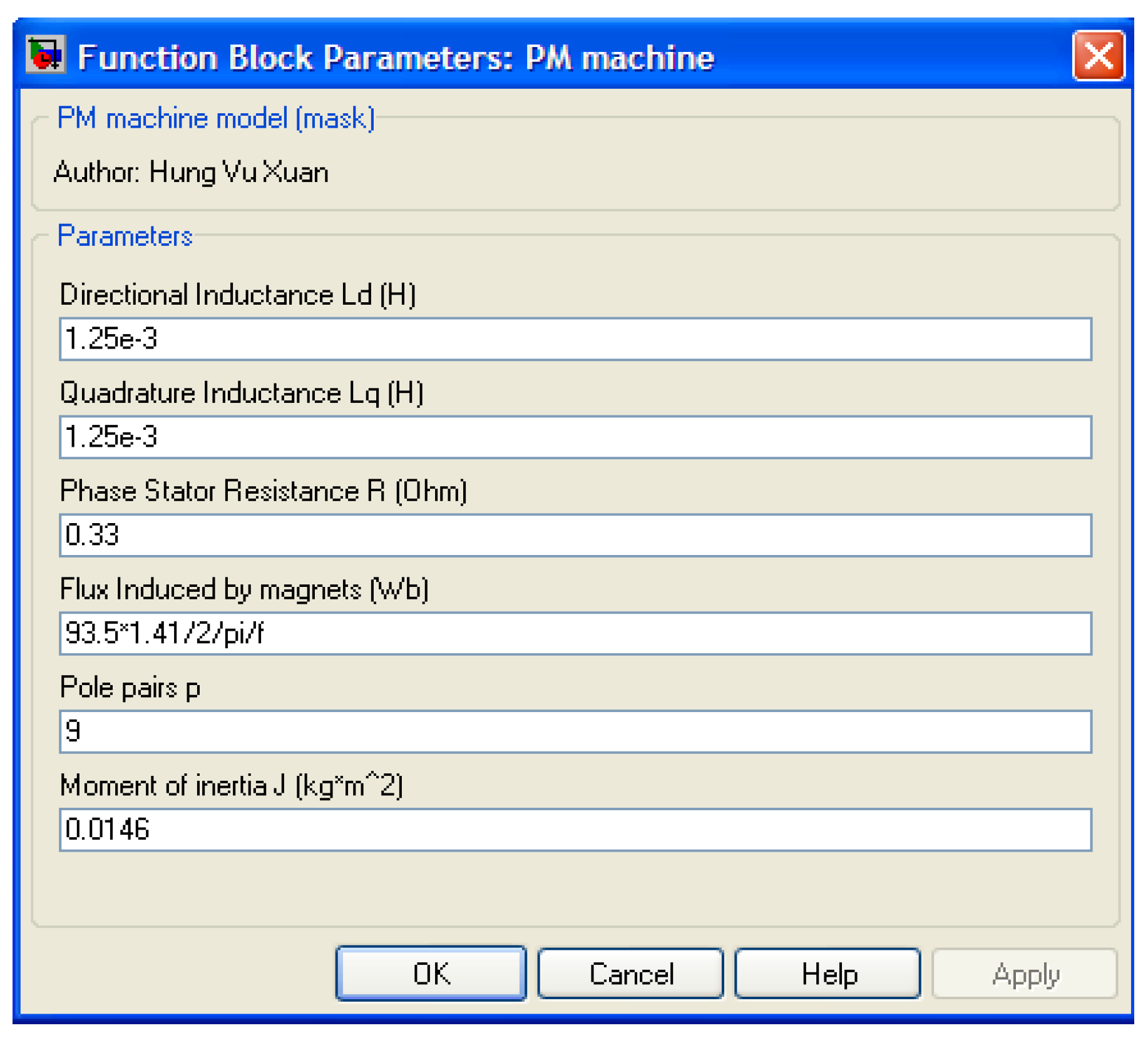
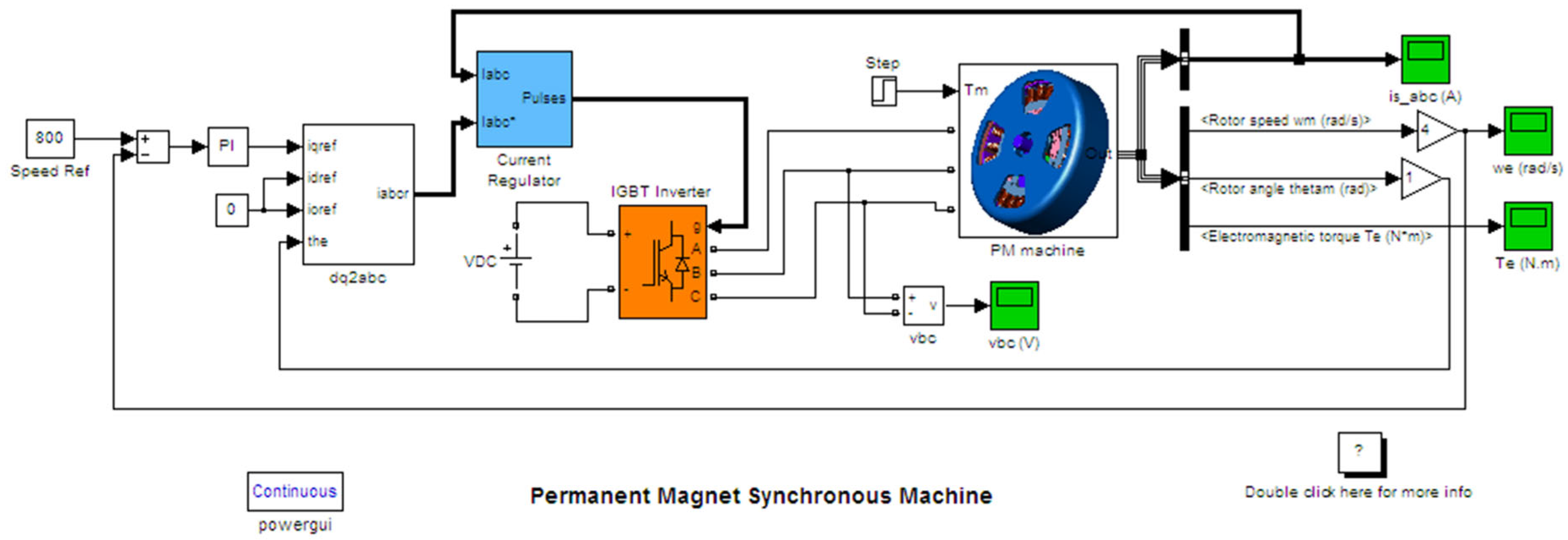
2.1. The d-q Model

We assume that the voltage, current and flux linkage of a PM machine are sinusoidal waves, the magnetic circuit is unsaturated and the PM machine has electrical and mechanical symmetry. A PM machine can be modeled in the d-q coordinator as follows.

Voltage equations of a PM machine in the stator coordinator (α, β):

$$u_s^s=R_s{i}_s^s+{\displaystyle \frac{d{\psi }_s^s}{dt}}$$

(1)

in Equation (1), $u_s^s$ is the stator voltage vector in the stator coordinator; the subscript “s” shows that it is the stator component and the superscript “s” indicates that it is in the stator coordinate. It is similar to stator current vector $i_s^s$ and stator flux vector ${\psi }_s^s$.

The voltage equation of the PM machine in the rotor field coordinator f(d, q) can be obtained by transforming Equation (1), presented in the stator coordinator, to the d-q coordinator as follows:

$$u_s^f=R_s{i}_s^f+{\displaystyle \frac{d{\psi }_s^f}{dt}}+j{\omega }_e{\psi }_s^f$$

(2)

Note that the formula transforms vector V from the stator coordinate to the rotor magnetic field coordinate, $V_s^f=V_s^s{e}^{-j\theta }$, where θ is angle between the d-axis and α-axis and ω_e is the angular speed of the rotor magnetic field vector, ω_e = dθ/dt.

The stator flux vector in the dq coordinate can be written as

$${\psi }_s^f=L_s{i}_s^f+{\psi }_p^f$$

(3)

$${\psi }_{sd}=L_d{i}_{sd}+{\psi }_p$$

(4)

$${\psi }_{sq}=L_q{i}_{sq}$$

(5)

In the equations above, L_s is stator inductance and L_d and L_q are, respectively, the direct and quadrature components of L_s.

Equation (4) can be rewritten as

$${\omega }_e{\psi }_{sd}=X_d{i}_{sd}+{\omega }_e{\psi }_p\hspace{1em}or\hspace{1em}{\omega }_e{\psi }_{sd}=X_d{i}_{sd}+E_q$$

(6)

where X_d and X_q are reactance in the d and q direction, respectively.

The relationship between the electromagnetic force and pole magnetic flux can be written as

$${\psi }_p =E_q/{\omega }_e =\sqrt{2} E_o/{\omega }_e$$

(7)

where ψ_p is the pole magnetic flux and E_q is the quadrature component of electromotive force vector, and E_o is the RMS of the phase fundamental electromotive force.

Equation (5) can be rewritten as

$${\omega }_e{\psi }_{sq}=X_q{i}_{sq}$$

(8)

$$L_d=L_{ad}+L_{\sigma }$$

(9)

$$L_q=L_{aq}+L_{\sigma }$$

(10)

where L_ad is the d-axis main armature inductance and L_σ is stator leakage inductance. The inductances can be obtained by experiment or FEM computation [13,14,15].

Substituting Equations (3)–(5) in Equation (2) gives the following equations:

$$u_{sd}=R_s{i}_{sd}+{\displaystyle \frac{d{\psi }_{sd}}{dt}}-{\omega }_e{L}_q{i}_{sq}\hspace{1em}or\hspace{1em}{u}_{sd}=R_s{i}_{sd}+L_d{\displaystyle \frac{d{i}_{sd}}{dt}}-{\omega }_e{L}_q{i}_{sq}$$

(11)

$$u_{sq}=R_s{i}_{sq}+{\displaystyle \frac{d{\psi }_{sq}}{dt}}+{\omega }_e{L}_d{i}_{sd}+{\omega }_e{\psi }_p\hspace{1em}or\hspace{1em}{u}_{sq}=R_s{i}_{sq}+L_q{\displaystyle \frac{d{i}_{sq}}{dt}}+{\omega }_e{L}_d{i}_{sd}+{\omega }_e{\psi }_p$$

(12)

Equations (11) and (12) are balanced voltage equations in the dq coordinate of a PM machine.

The electromagnetic torque equation can be written as [16,17]

$$T_e={\displaystyle \frac{3}{2}}p\mathrm{Im}\{{\psi }_s^{f*}{i}_s^f\}={\displaystyle \frac{3}{2}}p({\psi }_{sd}{i}_{sq}-{\psi }_{sq}{i}_{sd})={\displaystyle \frac{3}{2}}p\left({\psi }_p{i}_{sq}+i_{sd}{i}_{sq}(L_d-L_q)\right)$$

(13)

where Im{·} is a function to obtain the imagined part of a complex number and p is the number of pole pairs.

$$T_e={\displaystyle \frac{3}{2{\omega }_e}}p\left(E_q{i}_{sq}+i_{sd}{i}_{sq}(X_d-X_q)\right)$$

(14)

In Equation (14), the first term of the torque is called “magnet alignment torque”. The second term proportional to (X_d − X_q) is called “reluctance torque”. E_q is the quadrature component of the electromotive force vector.

Electromagnetic power can be calculated as

$$P_e=T_{e.}{\omega }_e/p=2\pi f.T_e/p=3\pi f\left({\psi }_p{i}_{sq}+i_{sd}{i}_{sq}(L_d-L_q)\right),$$

(15)

from pole magnetic flux, dq inductances, and active and reactive current.

Output electrical power can be written as

$$P_o={\displaystyle \frac{3}{2}}\mathrm{Re}(u_s{i}_s^{*})$$

(16)

where $i_s^{*}$ is the conjugate vector of the current vector i_s, and p is the number of pole pairs.

The motion equation for the motor operating mode can be expressed as

$${\displaystyle \frac{J}{p}}{\displaystyle \frac{d{\omega }_e}{dt}}=T_e-T_{mec}$$

(17)

where T_mec and J are the mechanical torque of the load and inertia moment of the load and rotor, respectively. All the above equations are right for both generator mode and motor mode. However, note that for the generator operating mode, the expression on the right of Equation (17) will be (T_mec − T_e). The above differential equations can be solved by the Runge–Kutta method or by building a model in Matlab Simulink or using the S-function in Matlab.

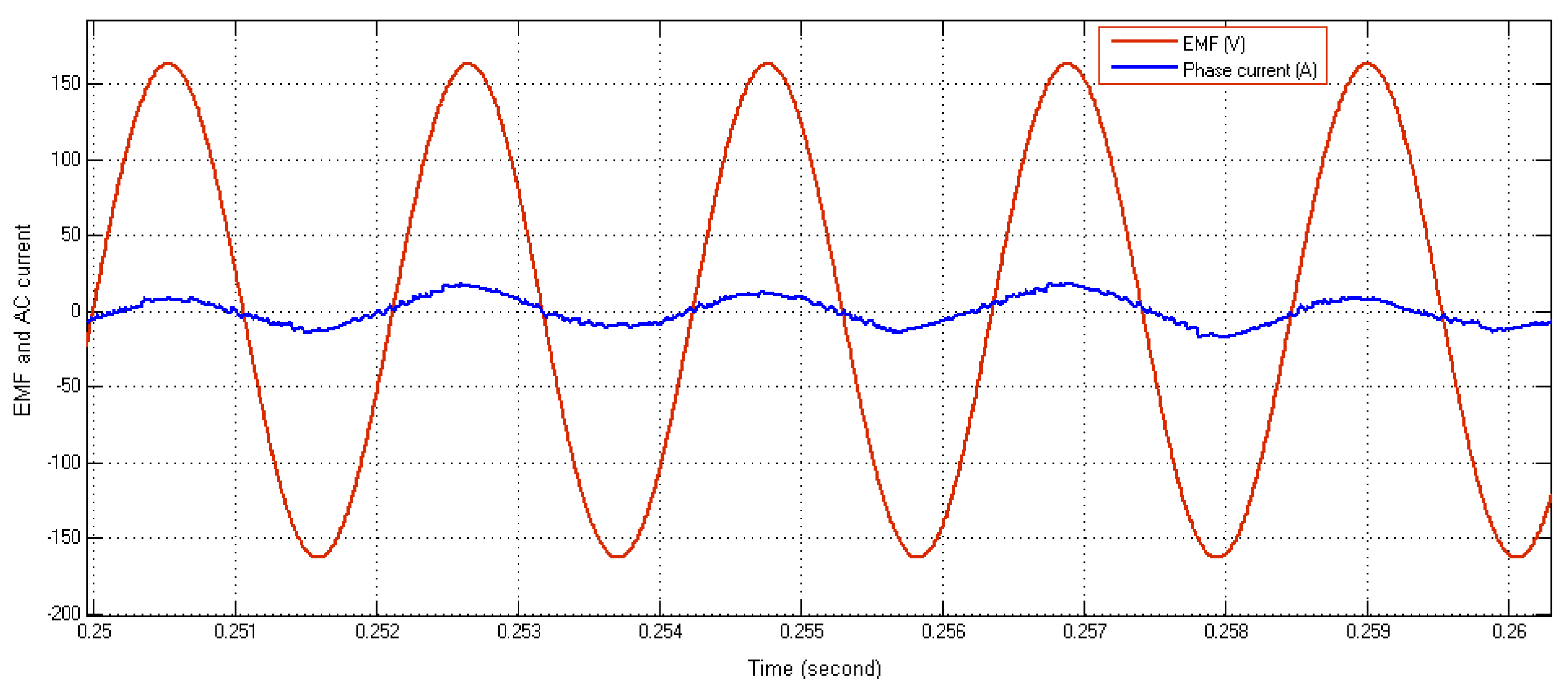
2.2. Simulation Model in Matlab/Simulink^®

A model of the PM machine in motor operating mode, built in Simulink/Matlab^® from Equations (2)–(5), (12) and (16), is shown in Figure 1.

This model can be used to study the starting of the PM generator and motor operating mode. The input data for this model includes directional inductance L_d, quadrature inductance L_q, phase resistance, flux induced by magnets ψ_p, pole pairs and the inertia moment of rotor and load. In Figure 1, the input parameters are three-phase voltages, and then they are converted into two-phase voltages in the dq coordinate. The u_sd and u_sq are inputs of a current model in the dq coordinate, which is described by Equations (11) and (12). The outputs of the current model are i_sd and i_sq, which are then used to calculate electromagnetic torque as (13). Finally, rotor speed is calculated according to (17).

Figure 2 is the interface menu built to enter data of the PM machine. Almost all parameters of the PM machine in Figure 2 have been estimated and validated by experiments, except for the inertia moment, which is an assumption-based calculation. The magnetic flux produced by magnets was calculated and validated using the experimental electromotive force.

Figure 3 is an example of the simulation of the PM machine working with a rotor field-oriented inverter in wind turbine pitch drive applications. In Figure 3, there are two closed loops; the inner closed loops are dq current loops and the outer closed loop is a speed loop. The PM machine block, which is a submodel, is modeled in the rotor field coordinate as described in Figure 1. With control construction, such as in Figure 3, the rotor speed, electromagnetic torque, and rotor flux of a PM machine with concentrated windings are controlled; the results are quite similar to those of PM machines with distributed windings, which are available in work such as [1,4] so they do not need to be mentioned here again.

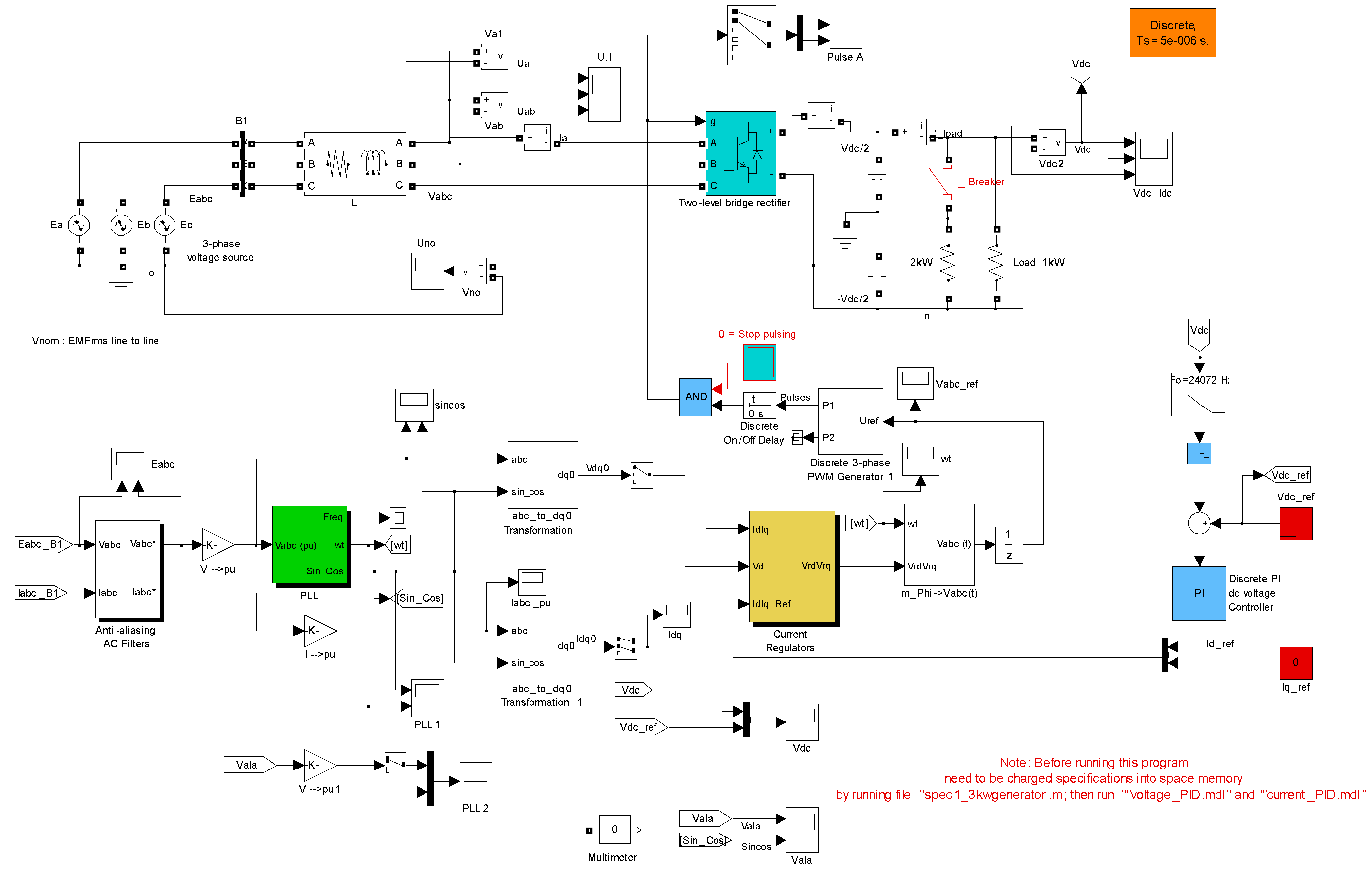
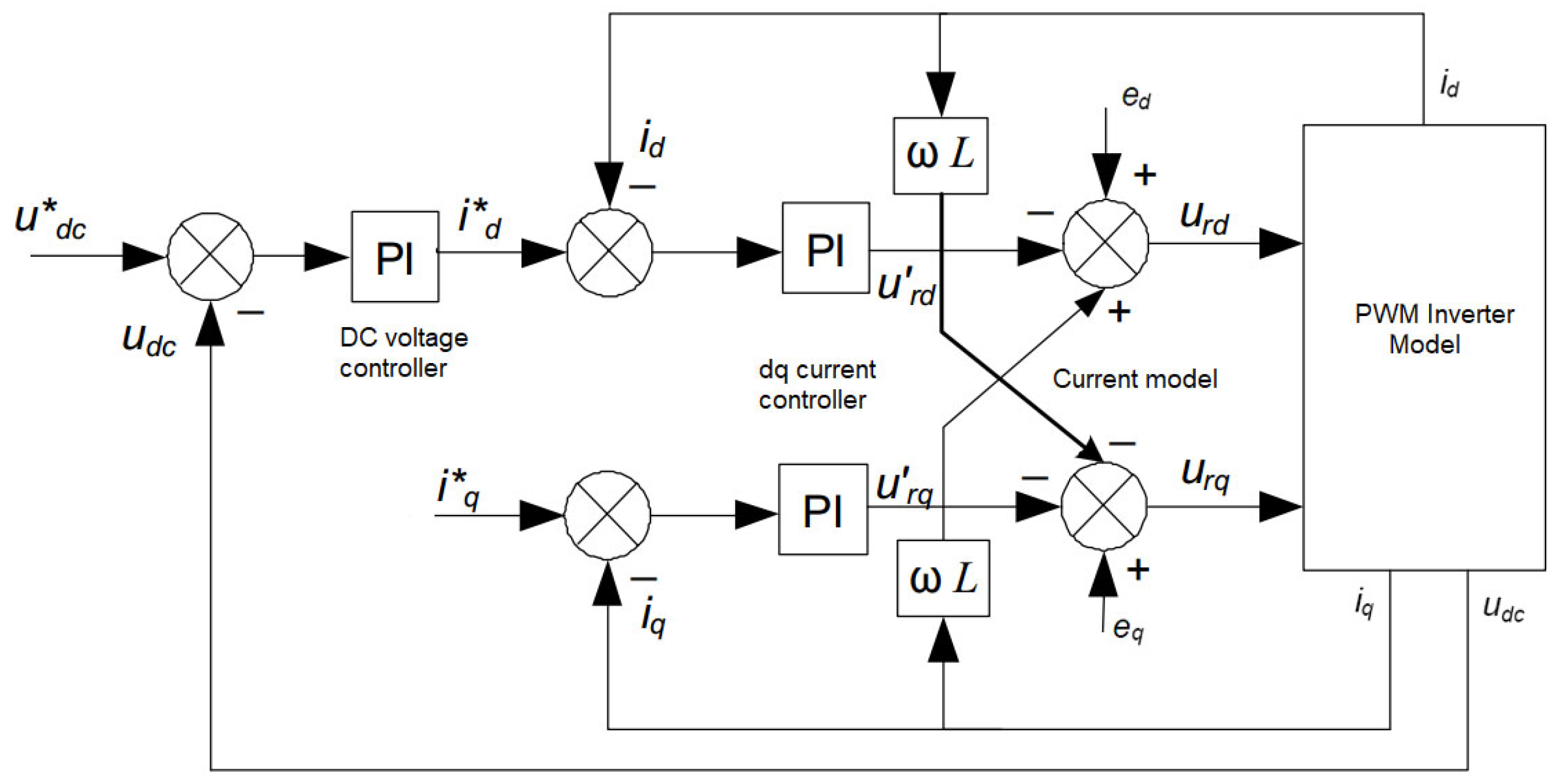
3. PM Generator Working with PWM Rectifier with Power Factor Controller

In this section, the modeling of an AC/DC converter with voltage-oriented control (VOC) is investigated. Figure 4 presents a simple equivalent circuit of a PMG working with an active rectifier load. The PMG is replaced with a three-phase electromotive force (EMF) system and inductances including resistances. We assume that the three-phase EMF system is symmetrical, so that the inductance of a phase is identical: L_a = L_b = L_c = L and resistance R_a = R_b = R_c = R. The dropped voltage on the switcher is ignored and the commutation of switches is neglected.

3.1. Mathematical Model for the PWM Rectifier in the (a, b, c) Frame Reference

The voltage equation for phase a can be written as [1,2,3,4,5,6,7,8]

$$L{\displaystyle \frac{d{i}_a}{dt}}+R{i}_a=e_a-u_{an}$$

(18)

$$u_{an}=u_{ao}+u_{on}$$

(19)

where the subscripts of voltages correspond to nodes in Figure 4; n is the neutral point of the generator, and o is the ground point of the DC bus.

S_a is defined as the switching function of a phase switch. When the upper switch T₁ is on, then S_a = 1 (and T₄ is off), and point “a” on Figure 4 is connected to point “d”, so that a ≡ d. Thus, the voltage u_ao = V_dc = S_aV_dc. If T₁ is off and T₄ is on, then S_a = 0 and point a is connected to point “o”, and a ≡ o; thus, the voltage u_ao = 0 = S_aV_dc. Similarly, the switching functions for S_b and S_c are also defined for phases b and c. The input voltage of the rectifier is defined as u_a $\equiv$ u_ao, u_b $\equiv$ u_bo, u_c $\equiv$ u_co. Therefore, the relationship between the input voltage of the rectifier, switching function and DC voltage can be written as

$$u_a=S_a{V}_{dc};\hspace{1em}{u}_b=S_b{V}_{dc};\hspace{1em}{u}_c=S_c{V}_{dc}.$$

(20)

For the three-wiring system, we always have

i_a + i_b +i_c = 0 and e_a + e_b + e_c = 0,

(21)

which means that the total three-phase current as well as the total three-phase symmetrical EMF equals zero.

For phase a, substituting (19) and (20) into (18), and similarly doing the same for phases b and c, the voltage equations can be rewritten as

$$L{\displaystyle \frac{d{i}_a}{dt}}+R{i}_a=e_a-(S_a{V}_{dc}+u_{on})$$

(22)

$$L{\displaystyle \frac{d{i}_b}{dt}}+R{i}_b=e_b-(S_b{V}_{dc}+u_{on})$$

(23)

$$L{\displaystyle \frac{d{i}_c}{dt}}+R{i}_c=e_c-(S_c{V}_{dc}+u_{on})$$

(24)

where u_on is voltage between the neutral point of source n and the ground of the DC bus.

The voltage u_on can be obtained by adding (22), (23) and (24) and considering (21); therefore, the voltage u_on can be written as

$$u_{on}=-{\displaystyle \frac{V_{dc}}{3}}{\displaystyle \sum _{k=a,b,c}{S}_k}.$$

(25)

Substituting (25) into Equations (22)–(24), the voltage equations can be rewritten as

$$L{\displaystyle \frac{d{i}_a}{dt}}+R{i}_a=e_a-({\displaystyle \frac{2}{3}}{S}_a-{\displaystyle \frac{S_b}{3}}-{\displaystyle \frac{S_c}{3}})V_{dc}$$

(26)

$$L{\displaystyle \frac{d{i}_b}{dt}}+R{i}_b=e_b-({\displaystyle \frac{2}{3}}{S}_b-{\displaystyle \frac{S_a}{3}}-{\displaystyle \frac{S_c}{3}})V_{dc}$$

(27)

$$L{\displaystyle \frac{d{i}_c}{dt}}+R{i}_c=e_c-({\displaystyle \frac{2}{3}}{S}_c-{\displaystyle \frac{S_b}{3}}-{\displaystyle \frac{S_a}{3}})V_{dc}.$$

(28)

For more compactness, Equations (22)–(24) can be rewritten in the matrix form as

$$L{\displaystyle \frac{d{i}_s}{dt}}+R{i}_s=e_s-u_r$$

(29)

In Equation (29), u_r is input voltage vector of the rectifier. It can be expressed as

$$u_r=(S.V_{dc}+D.u_{on})$$

(30)

where e_s is the electromotive force vector, u_r is the input voltage vector of the rectifier—which is the difference in the voltage vector between the input of rectifier and point o—and

i_s = [i_a, i_b, i_c]’; e_s = [e_a, e_b, e_c]’; u_r = [u_a, u_b, u_c]’; S= [S_a, S_b, S_c]’; D = [1, 1, 1]’. Note that the sign ( ‘ ) denotes for the transpose operator of a matrix.

Applying Kirchhoff’s law for node d in Figure 4, the direct current i_dc can be written as

$$i_{dc}=S_a{i}_a+S_b{i}_b+S_c{i}_c.$$

(31)

The current i_c through the DC capacitor C_d can be written as

$$i_c=C_d{\displaystyle \frac{d{V}_{dc}}{dt}}=i_{dc}-i_l\mathrm{or} C_d{\displaystyle \frac{d{V}_{dc}}{dt}}=S_a{i}_a+S_b{i}_b+S_c{i}_c-i_l.$$

(32)

The instantaneous apparent power s of the rectifier is defined as

$$s(t)=u_a{i}_a+u_b{i}_b+u_c{i}_c+j{\displaystyle \frac{1}{\sqrt{3}}}[(u_b-u_c)i_a+(u_c-u_a)i_b+(u_a-u_b)i_c].$$

(33)

The active power p and reactive power q are defined as

$$p(t)=u_a{i}_a+u_b{i}_b+u_c{i}_c$$

(34)

$$q(t)={\displaystyle \frac{1}{\sqrt{3}}}[(u_b-u_c)i_a+(u_c-u_a)i_b+(u_a-u_b)i_c].$$

(35)

3.2. The Mathematic Model for the PWM Rectifier in the (d-q) Coordinator

We assume that the voltages and currents of phases a, b and c are sinusoidal. By using Park’s transformation, Equation (29), written in the stationary (a, b, c) reference frame, is transformed into (36) in the rotating f(d, q) coordinate. The d-axis coincides with the electromotive force vector (EMF) of the generator and the q-axis is perpendicular to the d-axis, as shown in Figure 5. The d-q coordinator rotates with an angle speed ω_e = 2πf, where f is the frequency of the internal voltage of the generator. Note that the d-q coordinator described in this section is oriented according to the EMF vector so that it is different to the d-q rotating magnetic field coordinator of the permanent magnet machine [1,2,3,4].

The voltage equation of the PWM rectifier in the q-d coordinator can be described as

$$L{\displaystyle \frac{d{i}_s^f}{dt}}+j{\omega }_{e}L{i}_s^f+R{i}_s^f=e^f-u_r^f.$$

(36)

The vector Equation (36) is separated into the components in the d-axis and q-axis:

$$L{\displaystyle \frac{d{i}_d}{dt}}=e_d-R{i}_d+{\omega }_{e}L{i}_q-u_{rd}$$

(37)

$$L{\displaystyle \frac{d{i}_q}{dt}}=e_q-R{i}_q-{\omega }_{e}L{i}_d-u_{rq}$$

(38)

The input power of the rectifier can be expressed as

$$p\left(t\right)={\displaystyle \frac{3}{2}}\mathit{Re}(u_r^f{i}_r^{f*})={\displaystyle \frac{3}{2}}\left(u_{rd}{i}_d+u_{rq}{i}_q\right)$$

(39)

$$q\left(t\right)={\displaystyle \frac{3}{2}}\mathit{Im}(u_r^f{i}_r^{f*})={\displaystyle \frac{3}{2}}\left(-u_{rd}{i}_q+u_{rq}{i}_d\right)$$

(40)

The d-axis coincides with the internal voltage vector (so-called Voltage Oriented Control method—VOC) so that the q component of voltage u_q is equal to zero in steady state operation. The q-current component i_q is able to be controlled by the current controller so that the power factor can also be controlled. If the q-current is zero, the vector voltage and vector current will be unified, so that the power factor will be equal to 1. For the generator, the angle between the electromotive force and the current will not be measured directly, but it can estimate from the measured voltage and measured current.

Vector $u_r^{\prime f}$ is defined as follows

$$u_r^{\text{'}f}=u_{rd}^{\text{'}}+j{u}_{rq}^{\text{'}}$$

(41)

$$u_{rd}^{\text{'}}=L{\displaystyle \frac{d{i}_d}{dt}}+R{i}_d$$

(42)

$$u_{rq}^{\text{'}}=L{\displaystyle \frac{d{i}_q}{dt}}+R{i}_q.$$

(43)

Thus, substituting (42) and (43) into (37) and (38), we obtain

$$u_{rd}=-u_{rd}^{\text{'}}+{\omega }_{e}L{i}_q+e_d$$

(44)

$$u_{rq}=-u_{rq}^{\text{'}}-{\omega }_{e}L{i}_d+e_q$$

(45)

From Equations (44) and (45), the control diagram of a PWM rectifier, including the DC voltage closed loop and the current closed loops, can be presented as in Figure 6. In Figure 6, the DC voltage at the DC bus is controlled by the DC voltage controller. The output of the voltage controller is the setting value i_d* of the current control loop. The dq current model is formed from Equations (44) and (45). The vector current is decomposed into two separated currents, i_d and i_q. The inputs of the current model have set values of i_d* and i_q*. There are two current controllers for controlling the active and reactive current. The outputs of the current model have set dq voltages of u_rd and u_rq, which are the reference voltage for pulse width modulation (PWM). For few kilowatts PMM, the transient time for current response is normally a few milliseconds only, which is much quicker (normally at least 2 times quicker) than the transient time of the outer DC voltage loop. Therefore, the parameters of current controllers are key for the stability and control quality of the system, as will be discussed in a later section. If the set i_q* current is zero and there is a quick response in terms of current, the generator voltage and current vector will be in the same phase and the power factor will be 1.

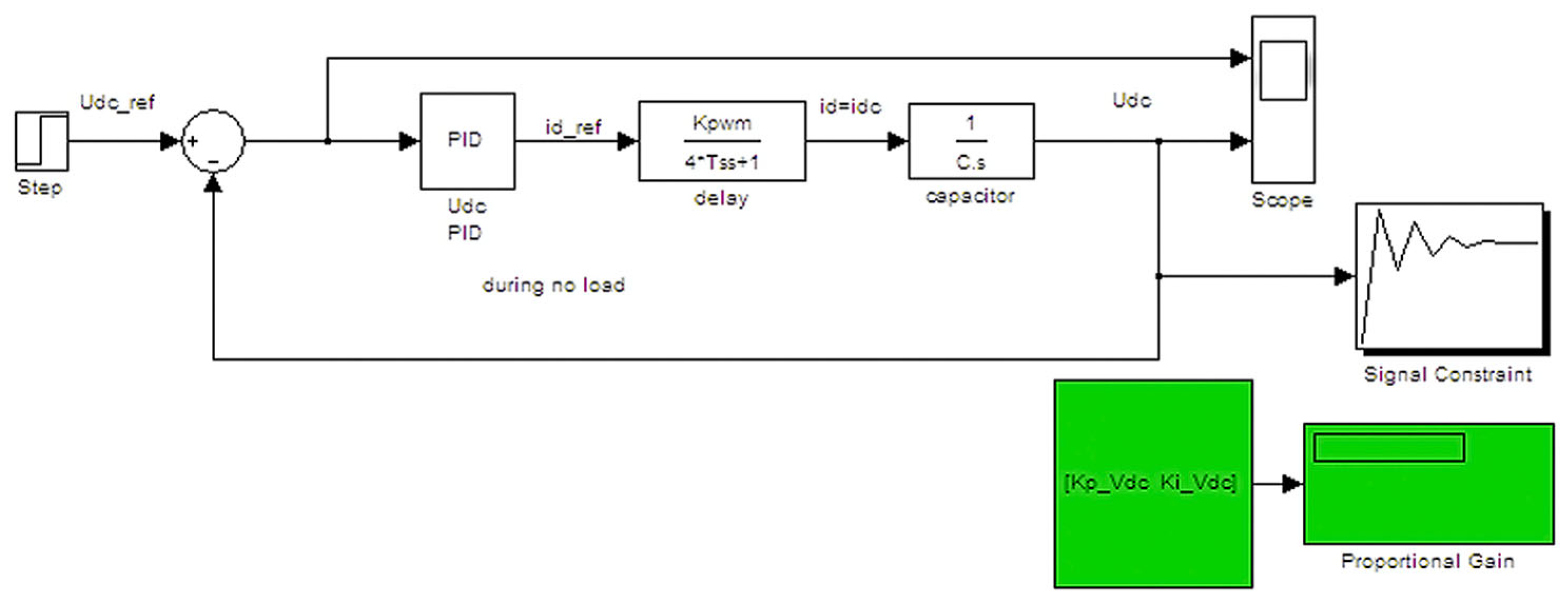
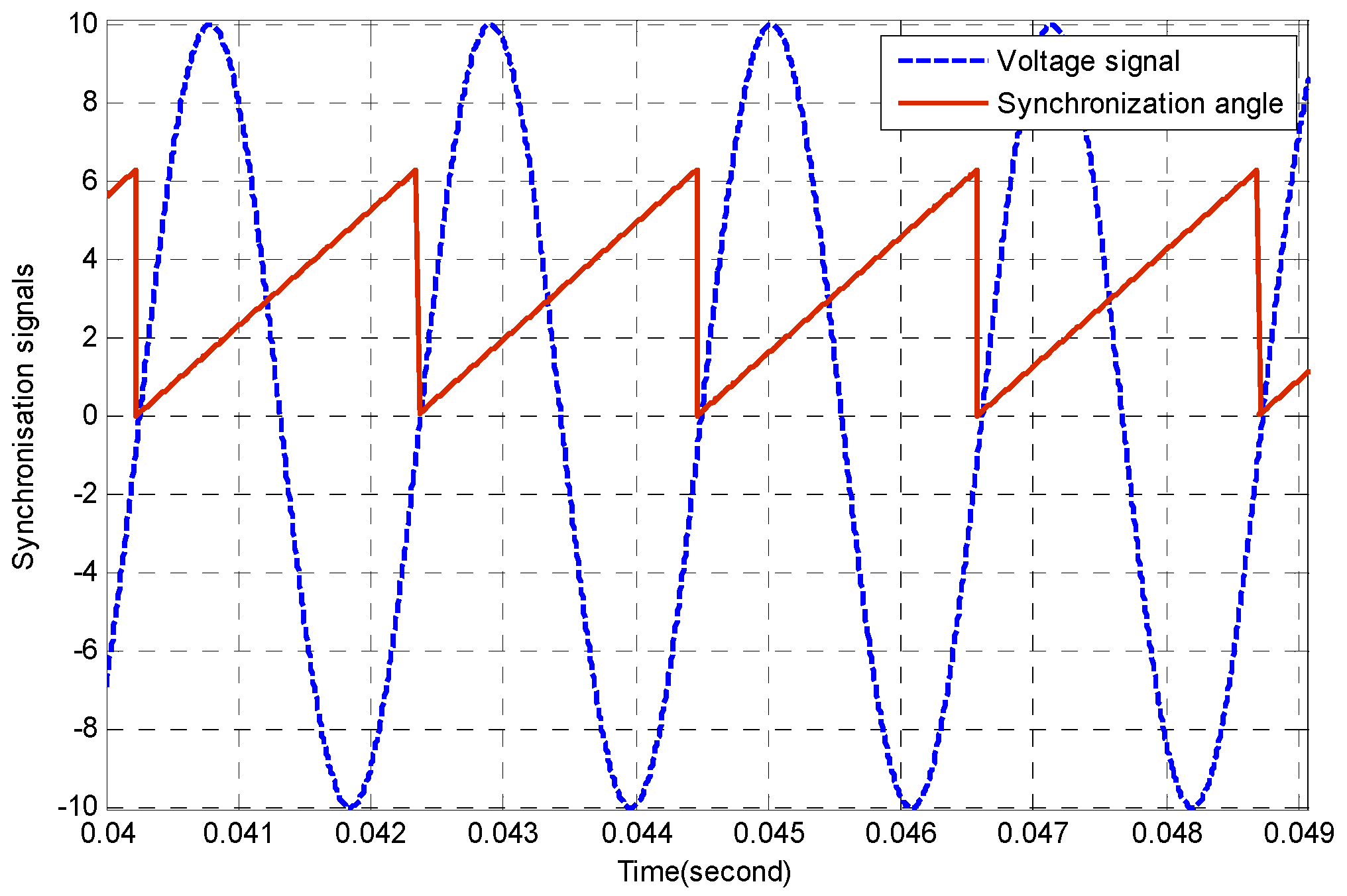
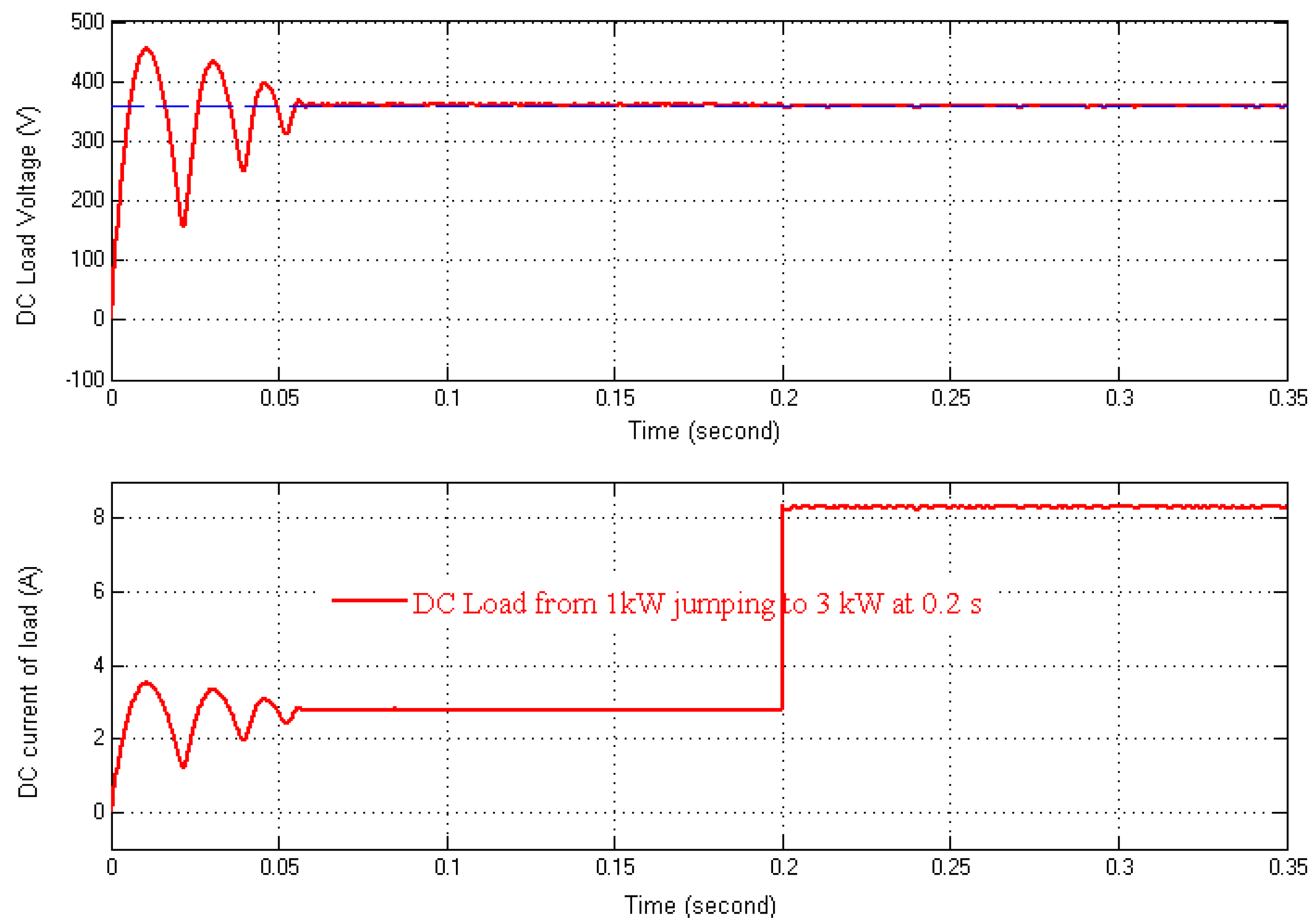
3.3. Simulation PWM Rectifier

Figure 7 presents the control construction of an active rectifier for a generator in standalone mode. The measured DC voltage is used as a feedback signal for the DC voltage control loop. The currents i_d and i_q are independently controlled together. Three-phase currents i_abc of the generator are measured, and are then converted into αβ components in a stationary coordinate using Clarke’s transformation and dq current components in RFC using Park’s transformation, which are used for current signal feedback in current control loops. For coordination conversion from the abc coordinate to the dq coordinate, the θ angle is determined by using Phase-Locked Loop (PLL). The input of the PLL block is from the generator three-phase voltage u_abc, which is measured before inductive filtering. It is worth mentioning that for better performance in terms of maximum generated power and eliminating inductive hard filter but with more complications, the generator three-phase voltage and current are measured. After that, the fundamental voltage and current are obtained via a software filter, and finally electromotive forces (EMFs) are calculated from the voltage-balanced equation. The calculated EMFs are used as the input of the PLL block. The structure and parameters of the PLL are determined as in [18,19,20,21].

The main parameters concerning DC capacitor, PMM inductance, rated no-load voltage (EMF), switching frequency and sampling time for simulation in Figure 8, Figure 9, Figure 10 and Figure 11 are as follows:

• Capacitor: C = 1.8 mF;
• Phase inductance of PM machine: L = 1.25 mH;
• Phase resistance of PM machine: R = 0.33 Ω;
• Line–line electromotive force of PM machine at 3000 rpm: EMF = 162 V;
• Carrier frequency or switching frequency: f_c = 51 * f = 51 * 472 = 24,072 Hz;
• Sampling time and sampling frequency: T_s = 5 μs, f_s =1/T_s = 200 kHz.

In order to determine the parameters of the current controllers and DC voltage controller, a model for each closed loop must be defined. Figure 8 is a closed loop for finding the parameters of the DC voltage controller, in which PWM is replaced by the first-order transfer function and the control object of the capacitor block of the DC bus. The delay time constant of the PWM transfer function became four times bigger than the sampling time. The amplifier constant of the PWM transfer function is equal to 1, meaning that the PWM output voltage can be mapped 1 to 1 on amplitude, but the delay time is four cycles of sampling time.

Figure 9 is a closed loop for finding the parameters of the current controller. The control object of the electrical current loop involves generator winding resistance and inductance. Therefore, the control object is the first-order transfer function, in which the amplifier and time constant are calculated from the generator resistance and inductance. A delay time block with a delay time double the sampling time is inserted between the current controller and its control object. Figure 10 shows the detail of PI current controllers implemented in Simulink/Matlab^®. The parameters of controllers are determined by using the PID auto-tune tool in Matlab when running control loops in Figure 8 and Figure 9. The determined parameters of the controllers will be used in a whole simulation of the PWM converter–PM generator system, as described in Figure 11. Figure 11 shows the whole simulation blocks in Matlab Simulink, including the models of the generator, PWM converter, controllers, and DC load, the measurement of the DC voltage, three-phase generator voltage and three-phase current, and PLL for determining synchronous θ angle, which is used to convert the generator three-phase current i_abc to two-phase i_dq. The PWM block is implemented by comparing the carrier signal to three-phase reference signals, which are obtained from outputs of the current controller after converting. The output signals of the PWM block are used to control the switchers of the converter. The PWM signals to control the upper-leg switcher and lower-leg switcher are opposites. Additionally, a dead time is taken into account to prevent short-circuiting of the DC bus and to protect the switchers from short-circuit current.

Figure 8. Closed loop for finding parameters of PI dc-voltage controller using PID tune tool in Matlab.

Figure 8. Closed loop for finding parameters of PI dc-voltage controller using PID tune tool in Matlab.

Figure 9. Closed loop for finding parameters of PI current controller using PID tune tool in Matlab.

Figure 9. Closed loop for finding parameters of PI current controller using PID tune tool in Matlab.

Figure 10. Structure of current controller in Simulink.

Figure 10. Structure of current controller in Simulink.

Figure 11. Simulation of whole generator-PWM rectifier system with power factor control.

Figure 11. Simulation of whole generator-PWM rectifier system with power factor control.

It can be seen from Figure 12 that the θ angle, output signal of the PLL block and a triangle signal synchronize to the voltage signal of phase a and vary from 0 to 2π in one voltage cycle. This figure also shows that the PLL block works well to meet the requirements for synchronization. This requirement is crucial for voltage-oriented control.

Figure 13, Figure 14 and Figure 15 show some simulation results of the PWM converter–PM generator system. Figure 13 shows the DC voltage and current during charging and steady state. It also shows that DC voltage is kept constant and follows the setting value with negligible error in steady state, even with load jumping from 1 kW to 3 kW at the moment of 0.2 s in the simulation. It can be seen from Figure 14 that the phase EMF and phase current are in phase unity. Figure 15 shows the PWM voltage and current of the active converter. All simulation results prove that the parameters of current and dc voltage controls are well estimated.

4. Conclusions

This paper has presented mathematic models for both a PM generator with fractional-slot concentrated windings and an active rectifier in the dq coordinate. The model was built, simulated and verified in Simulink Matlab to prove the accuracy of the developed model. The effective method to define parameters of the current controller and DC voltage controller were presented. The simulation result with real specifications of a real external PM generator with concentrated windings show that the current response and DC voltage also follow the setting values. Thanks to the quick responses of the dq current, the phases of generator voltage and current are unified or show a generator power factor of 1.