Entropy-Based Optimization in Chaotic Image Encryption Algorithms with Implementation of Artificial Intelligence †
Abstract
1. Introduction
2. Materials and Methods
2.1. Lorenz Chaotic System
2.2. Chaos-Based Encryption Algorithms
3. Entropy-Based Optimization Through the Application of the Price Method and Artificial Intelligence
3.1. Entropy as a Criterion for Optimality
3.2. Modified Price’s Method for Finding the Global Extremum
4. Results and Analysis
4.1. Results of the Encoding Algorithm
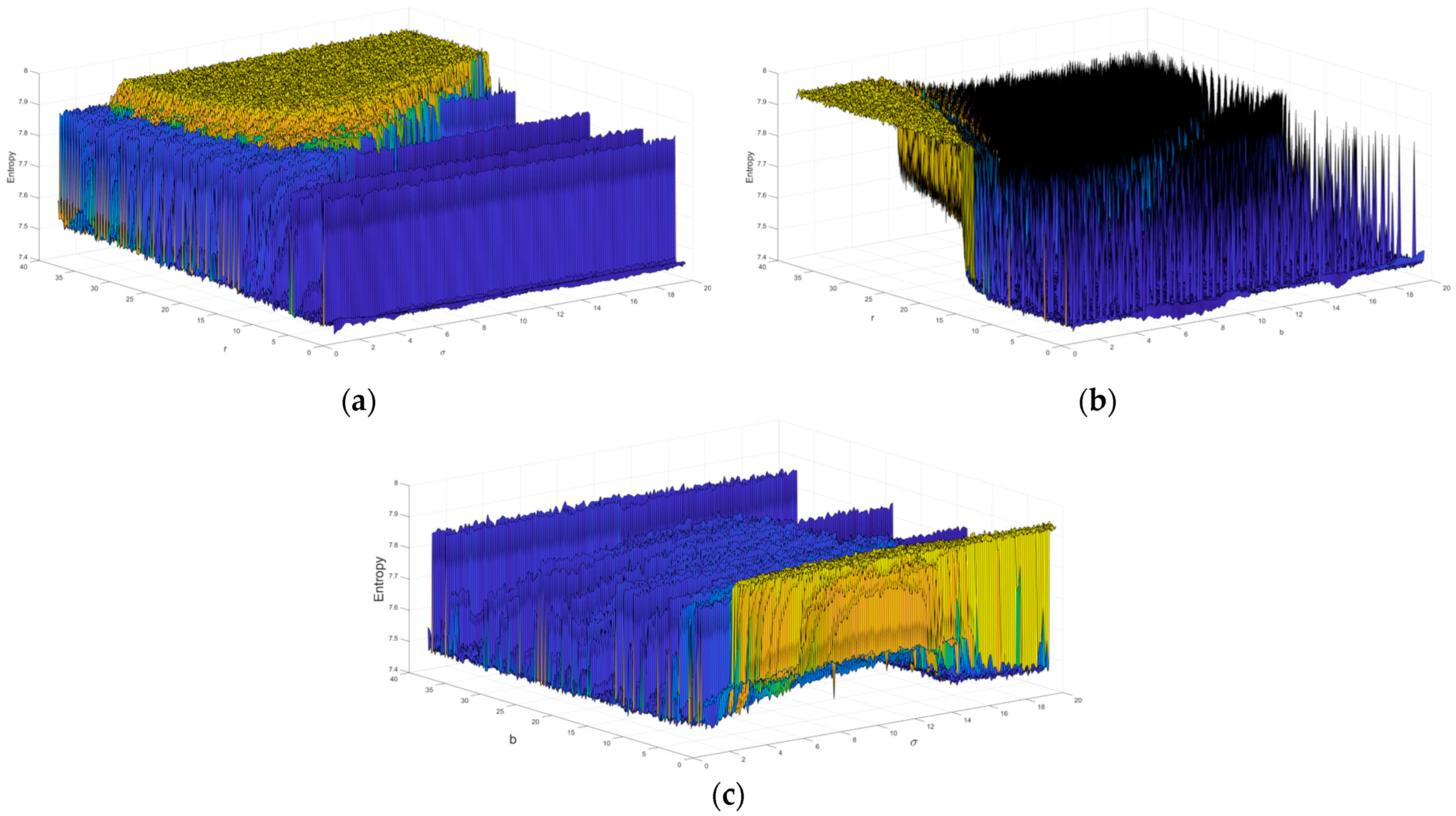
4.2. Results from the Analysis of the Objective Function with Respect to Image Size
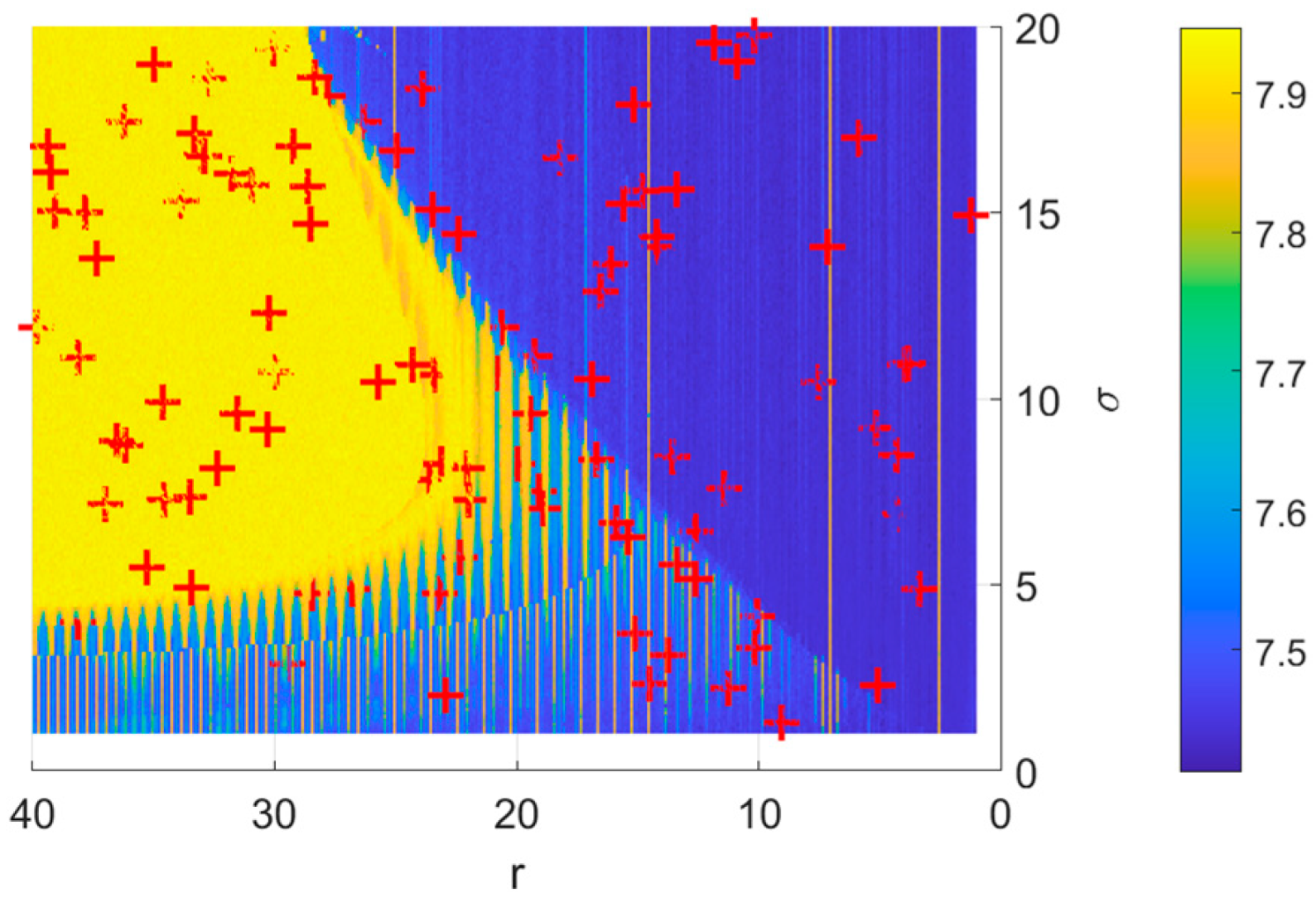
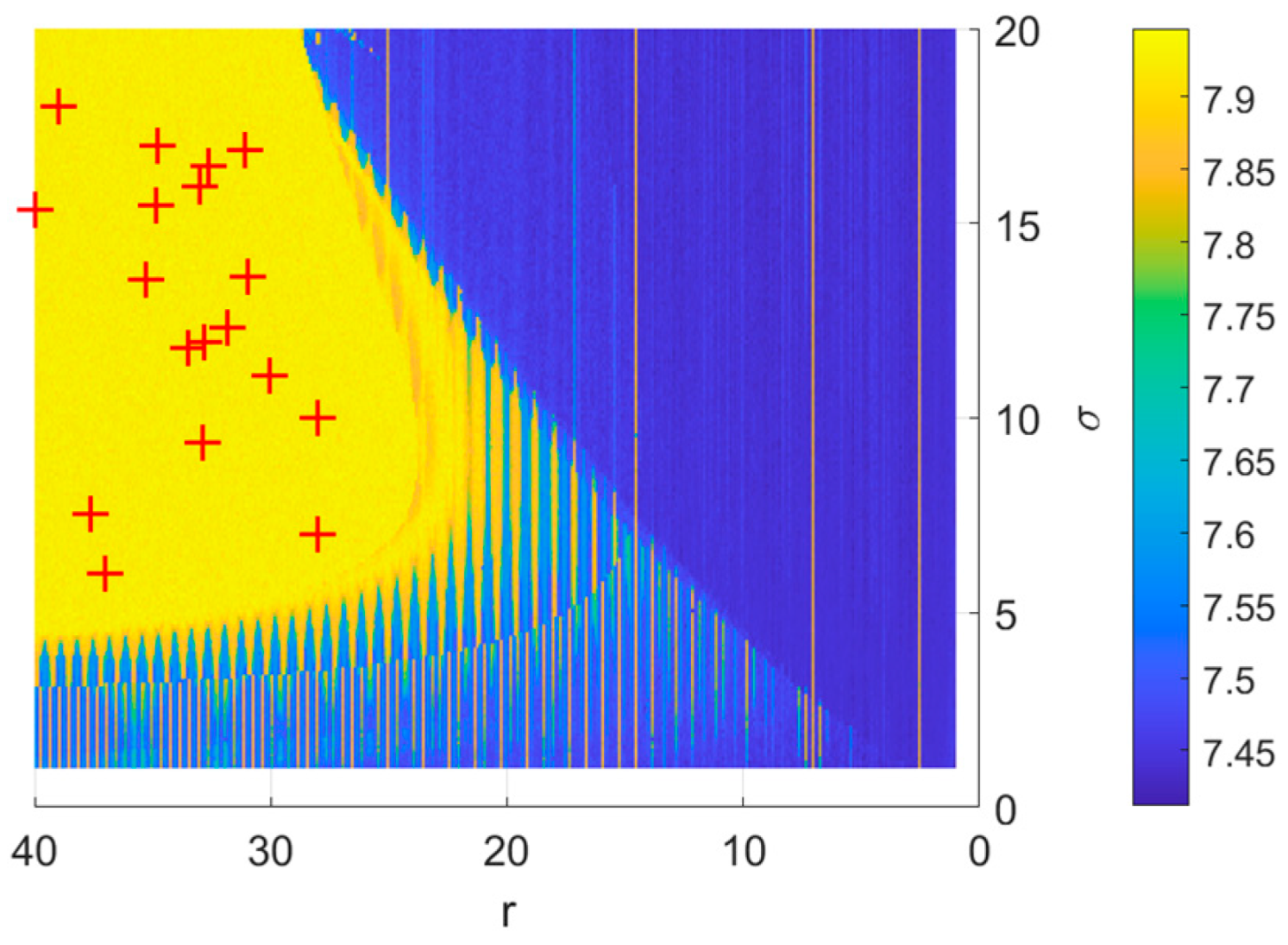
4.3. Results from the Application of the Price Algorithm with AI for Determining the Optimal Parameters of the Chaotic System
4.4. Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahmed, S.T.; Hammood, D.A.; Chisab, R.F.; Al-Naji, A.; Chahl, J. Medical Image Encryption: A Comprehensive Review. Computers 2023, 12, 160. [Google Scholar] [CrossRef]
- Huang, Q.X.; Yap, W.L.; Chiu, M.Y.; Sun, H.M. Privacy-preserving deep learning with learnable image encryption on medical images. IEEE Access 2022, 10, 66345–66355. [Google Scholar] [CrossRef]
- Lai, Q.; Hu, G.; Erkan, U.; Toktas, A. High-efficiency medical image encryption method based on 2D Logistic-Gaussian hyperchaotic map. Appl. Math. Comput. 2023, 442, 127738. [Google Scholar] [CrossRef]
- El-Shafai, W.; Khallaf, F.; El-Rabaie, E.S.M.; El-Samie, F.E.A. Proposed 3D chaos-based medical image cryptosystem for secure cloud-IoMT eHealth communication services. J. Ambient Intell. Humaniz. Comput. 2024, 15, 1–28. [Google Scholar] [CrossRef]
- Nadhan, A.S.; Jacob, I.J. Enhancing healthcare security in the digital era: Safeguarding medical images with lightweight cryptographic techniques in IoT healthcare applications. Biomed. Signal Process. Control 2024, 88, 105511. [Google Scholar] [CrossRef]
- Alexan, W.; Aly, L.; Korayem, Y.; Gabr, M.; El-Damak, D.; Fathy, A.; Mansour, H.A. Secure communication of military reconnaissance images over UAV-assisted relay networks. IEEE Access 2024, 12, 78589–78610. [Google Scholar] [CrossRef]
- Kumar, R.; Khan, R.A. Securing communication protocols in military computing. Netw. Secur. 2024, 2024. [Google Scholar] [CrossRef]
- Kannan, B.M.; Solainayagi, P.; Azath, H.; Murugan, S.; Srinivasan, C. Secure Communication in IoT-enabled Embedded Systems for Military Applications using Encryption. In Proceedings of the 2023 2nd International Conference on Edge Computing and Applications (ICECAA), Namakkal, India, 19–21 July 2023; pp. 1385–1389. [Google Scholar] [CrossRef]
- Al-Sumaidaee, G.; Žilić, Ž. Sensing Data Concealment in NFTs: A Steganographic Model for Confidential Cross-Border Information Exchange. Sensors 2024, 24, 1264. [Google Scholar] [CrossRef]
- Shi, L.; Li, X.; Jin, B.; Li, Y. A Chaos-Based Encryption Algorithm to Protect the Security of Digital Artwork Images. Mathematics 2024, 12, 3162. [Google Scholar] [CrossRef]
- Aparna, H.; Madhumitha, J. Combined image encryption and steganography technique for enhanced security using multiple chaotic maps. Comput. Electr. Eng. 2023, 110, 108824. [Google Scholar] [CrossRef]
- Nasr, M.A.; El-Shafai, W.; El-Rabaie, E.S.M.; El-Fishawy, A.S.; El-Hoseny, H.M.; Abd El-Samie, F.E.; Abdel-Salam, N. A robust audio steganography technique based on image encryption using different chaotic maps. Sci. Rep. 2024, 14, 22054. [Google Scholar] [CrossRef]
- Gupta, M.; Singh, V.P.; Gupta, K.K.; Shukla, P.K. An efficient image encryption technique based on two-level security for internet of things. Multimed. Tools Appl. 2023, 82, 5091–5111. [Google Scholar] [CrossRef]
- Al-Batah, M.S.; Alzboon, M.S.; Alzyoud, M.; Al-Shanableh, N. Enhancing image cryptography performance with block left rotation operations. Appl. Comput. Intell. Soft Comput. 2024, 2024, 3641927. [Google Scholar] [CrossRef]
- Umar, T.; Nadeem, M.; Anwer, F. Chaos based image encryption scheme to secure sensitive multimedia content in cloud storage. Expert Syst. Appl. 2024, 257, 125050. [Google Scholar] [CrossRef]
- Rahul, B.; Kuppusamy, K. Efficiency analysis of cryptographic algorithms for image data security in cloud environment. IETE J. Res. 2023, 69, 6053–6064. [Google Scholar] [CrossRef]
- Neetha, S.S.; Bhuvana, J.; Suchithra, R. An efficient image encryption reversible data hiding technique to improve payload and high security in cloud platforms. In Proceedings of the 2023 6th International Conference on Information Systems and Computer Networks (ISCON), Mathura, India, 3–4 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Bajaj, H.; Das, P.; Mandal, S. Chaos Based Novel Video Encryption Scheme to Secure Video/Image Information from Any AI-Generated Attacks. J. Adv. Res. Appl. Sci. Eng. Technol. 2025, 50, 1–20. [Google Scholar] [CrossRef]
- Dhingra, D.; Dua, M. A chaos-based novel approach to video encryption using dynamic S-box. Multimed. Tools Appl. 2024, 83, 1693–1723. [Google Scholar] [CrossRef]
- Kumari, S.; Dua, M.; Dua, S.; Dhingra, D. A novel Cosine-Cosine chaotic map-based video encryption scheme. J. Eng. Appl. Sci. 2024, 71, 36. [Google Scholar] [CrossRef]
- Van Daalen, O.L. The right to encryption: Privacy as preventing unlawful access. Comput. Law Secur. Rev. 2023, 49, 105804. [Google Scholar] [CrossRef]
- Abusham, E.; Ibrahim, B.; Zia, K.; Rehman, M. Facial Image Encryption for Secure Face Recognition System. Electronics 2023, 12, 774. [Google Scholar] [CrossRef]
- Terziyan, V.; Malyk, D.; Golovianko, M.; Branytskyi, V. Encryption and generation of images for privacy-preserving machine learning in smart manufacturing. Procedia Comput. Sci. 2023, 217, 91–101. [Google Scholar] [CrossRef]
- Alghamdi, Y.; Munir, A. Image encryption algorithms: A survey of design and evaluation metrics. J. Cybersecur. Priv. 2024, 4, 126–152. [Google Scholar] [CrossRef]
- Saraiva, P. On Shannon entropy and its applications. Kuwait J. Sci. 2023, 50, 194–199. [Google Scholar] [CrossRef]
- Alhijawi, B.; Awajan, A. Genetic algorithms: Theory, genetic operators, solutions, and applications. Evol. Intell. 2024, 17, 1245–1256. [Google Scholar] [CrossRef]
- Papazoglou, G.; Biskas, P. Review and Comparison of Genetic Algorithm and Particle Swarm Optimization in the Optimal Power Flow Problem. Energies 2023, 16, 1152. [Google Scholar] [CrossRef]
- Mehmood, F.; Ahmad, S.; Whangbo, T.K. An Efficient Optimization Technique for Training Deep Neural Networks. Mathematics 2023, 11, 1360. [Google Scholar] [CrossRef]
- Bian, K.; Priyadarshi, R. Machine learning optimization techniques: A Survey, classification, challenges, and Future Research Issues. Arch. Comput. Methods Eng. 2024, 31, 4209–4233. [Google Scholar] [CrossRef]
- Zhan, T.; Shi, C.; Shi, Y.; Li, H.; Lin, Y. Optimization techniques for sentiment analysis based on llm (gpt-3). arXiv 2024, arXiv:2405.09770. [Google Scholar] [CrossRef]
- Li, L. A novel chaotic map application in image encryption algorithm. Expert Syst. Appl. 2024, 252, 124316. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.; Ma, C. Constructing dynamic strong S-Box using 3D chaotic map and application to image encryption. Multimed. Tools Appl. 2023, 82, 23899–23914. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, L. Chaos-Based Image Encryption: Review, Application, and Challenges. Mathematics 2023, 11, 2585. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Gao, M.; Tian, Y.; Wang, C.; Iu, H.H.-C. A Color Image Encryption Algorithm Based on Hash Table, Hilbert Curve and Hyper-Chaotic Synchronization. Mathematics 2023, 11, 567. [Google Scholar] [CrossRef]
- Stoycheva, H.; Mihalev, G.; Sadinov, S.; Angelov, K. Implementation of Chaotic Synchronization and Artificial Neural Networks in Modified OTP Scheme for Image Encryption. J. Imaging 2025, 11, 121. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, E.N. Deterministic Nonperiodic Flow 1. In Universality in Chaos, 2nd ed.; Routledge: London, UK, 2017; pp. 367–378. [Google Scholar]
- Price, W. Global optimization by controlled random search. J. Optim. Theory Appl. 1983, 40, 333–348. [Google Scholar] [CrossRef]
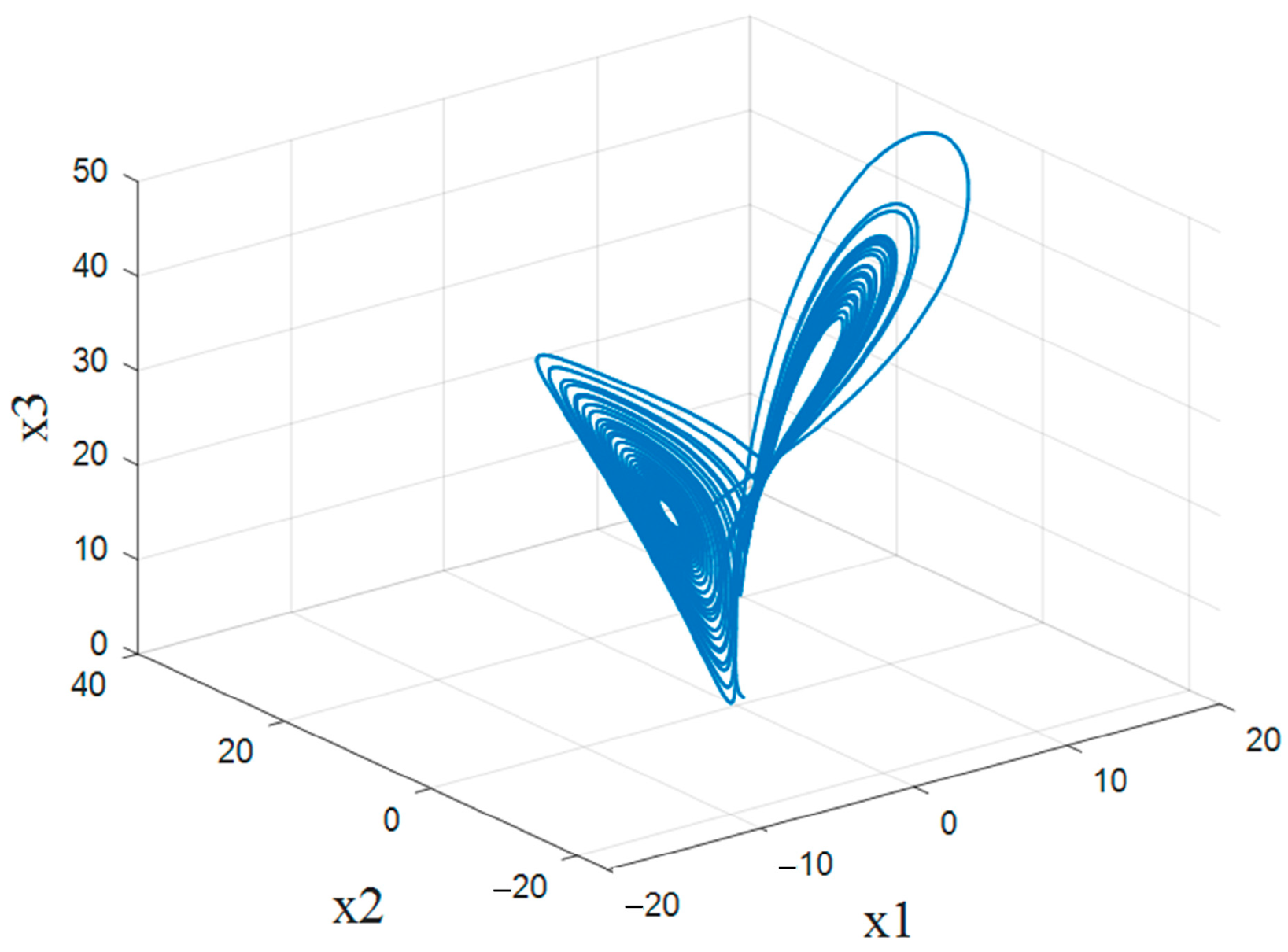
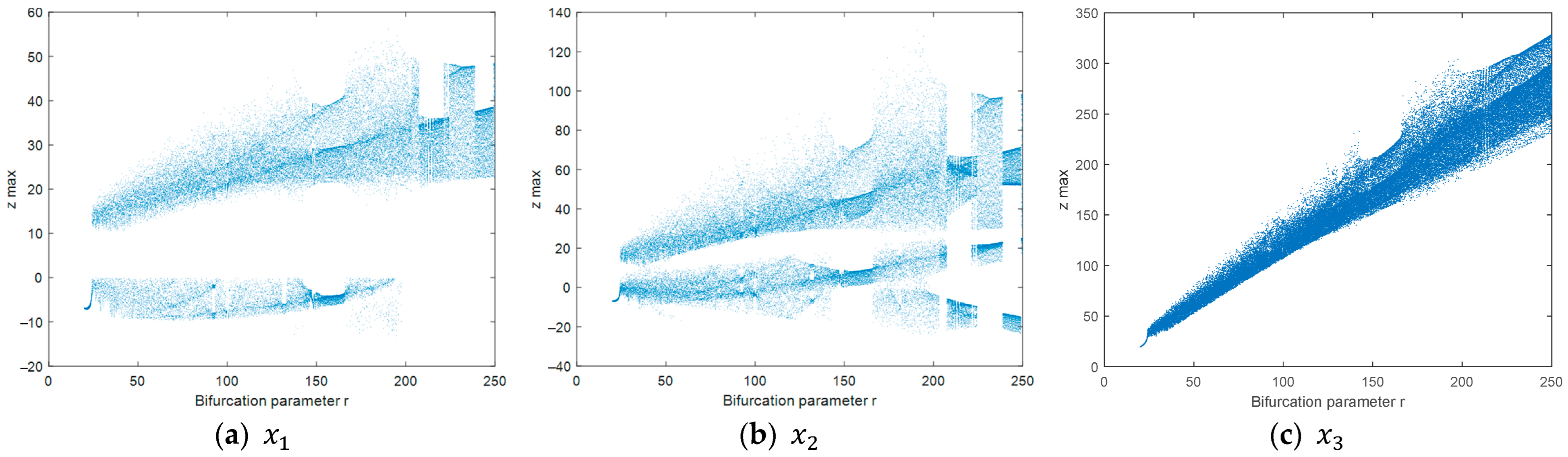

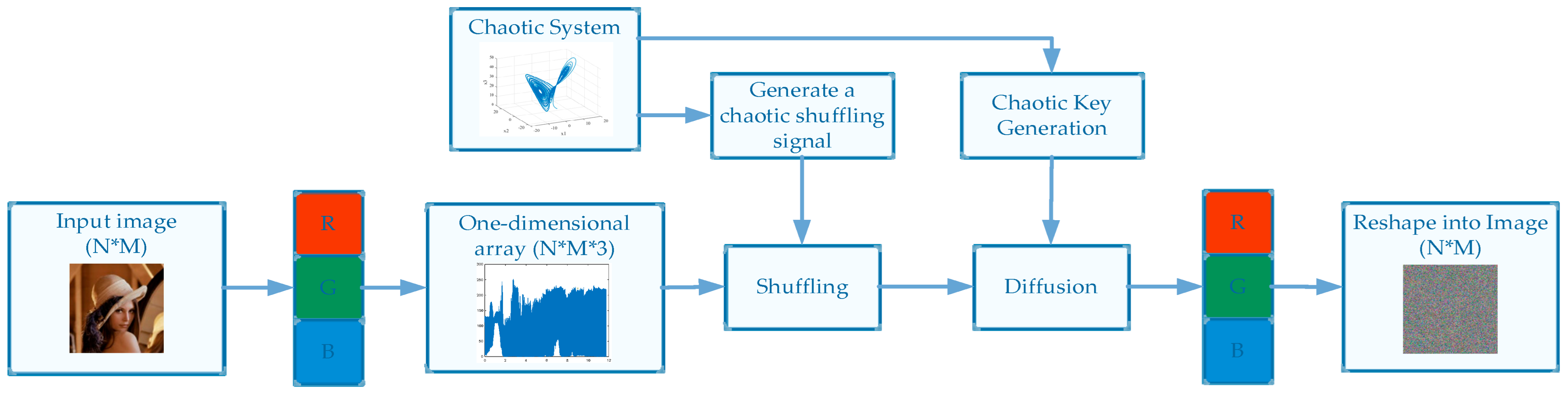
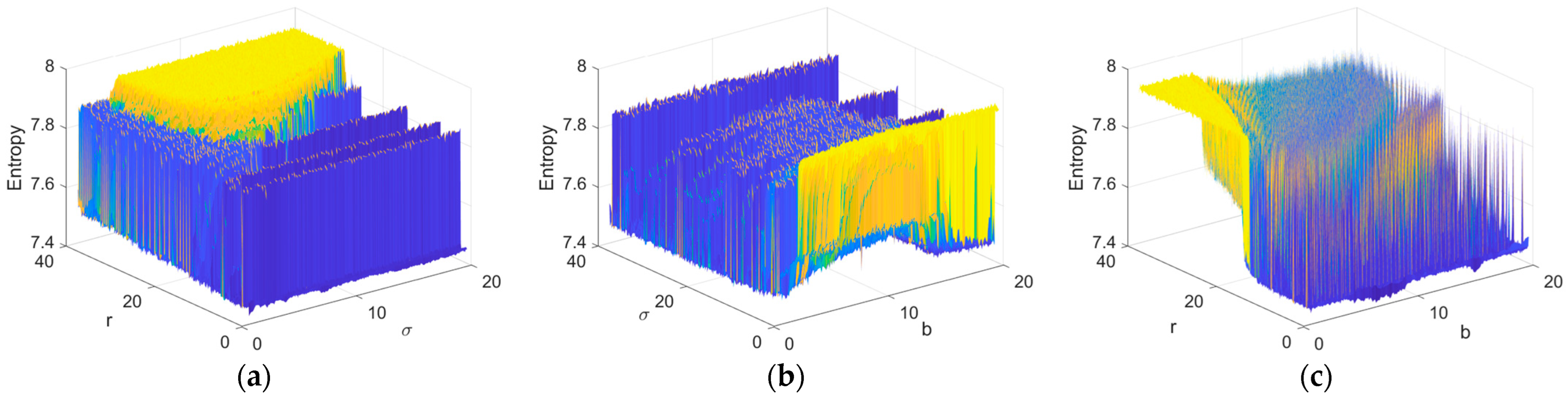
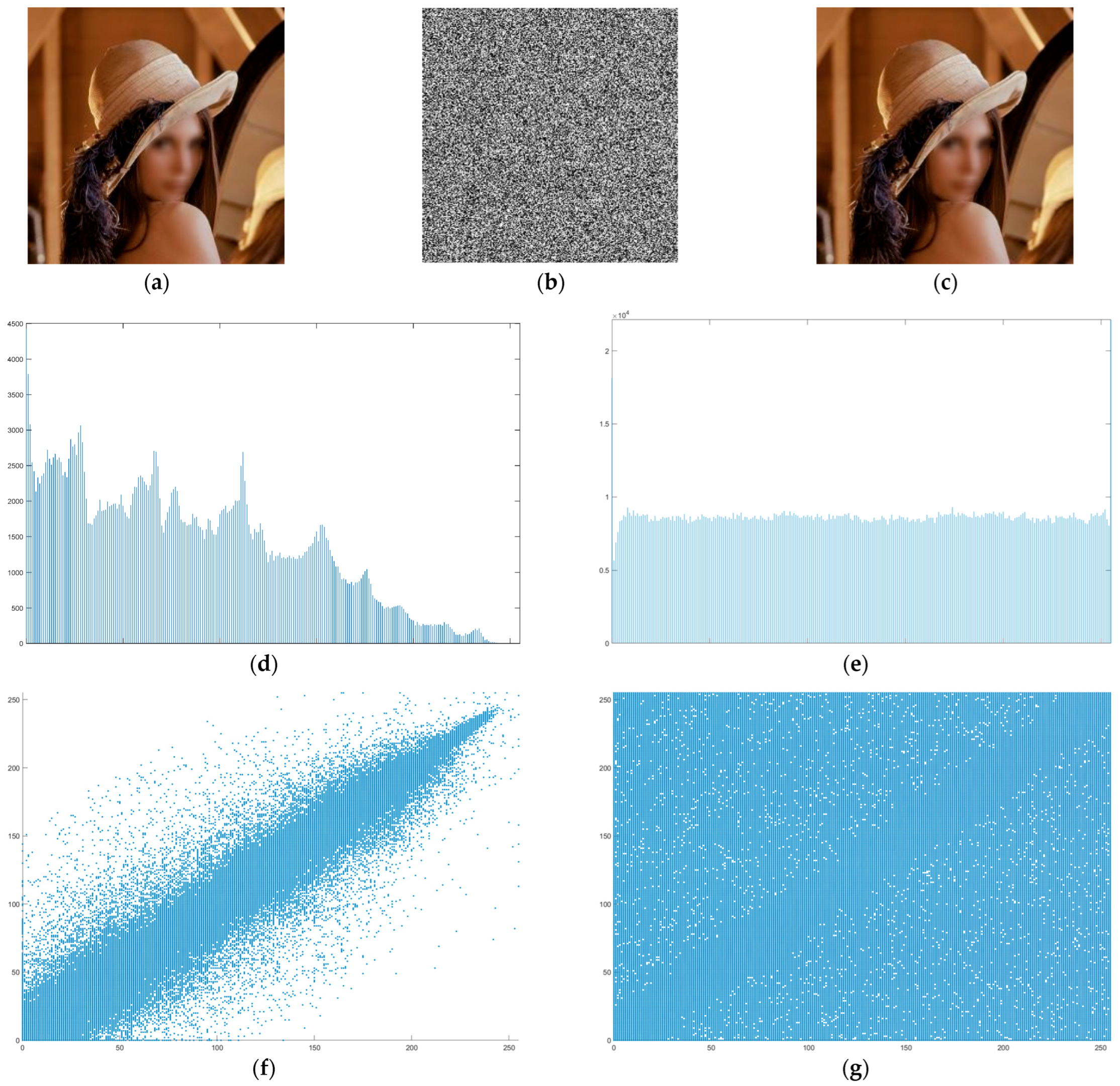

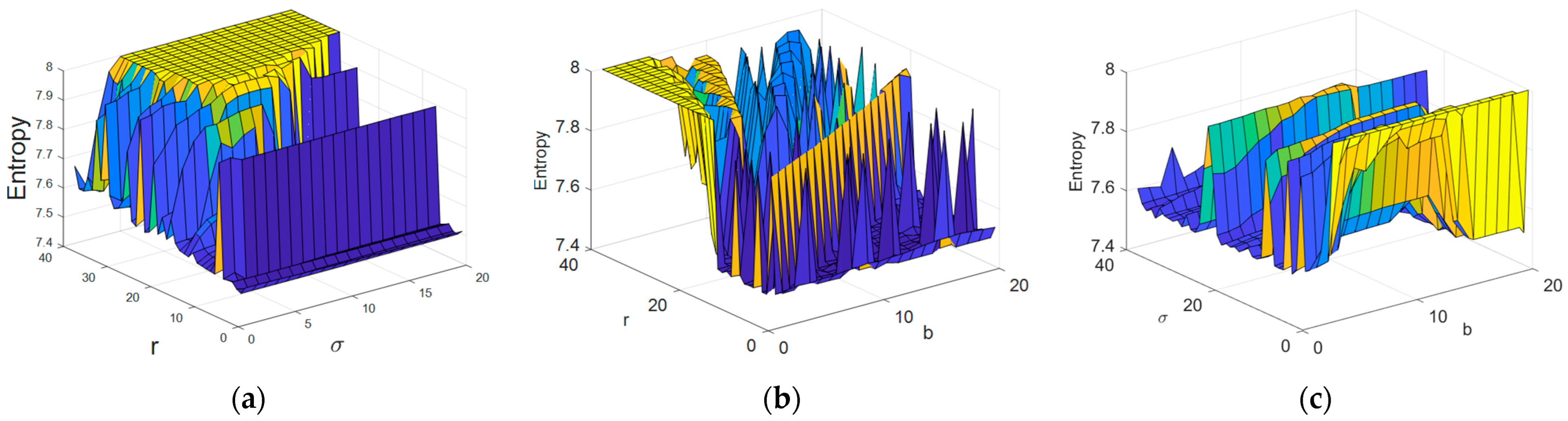
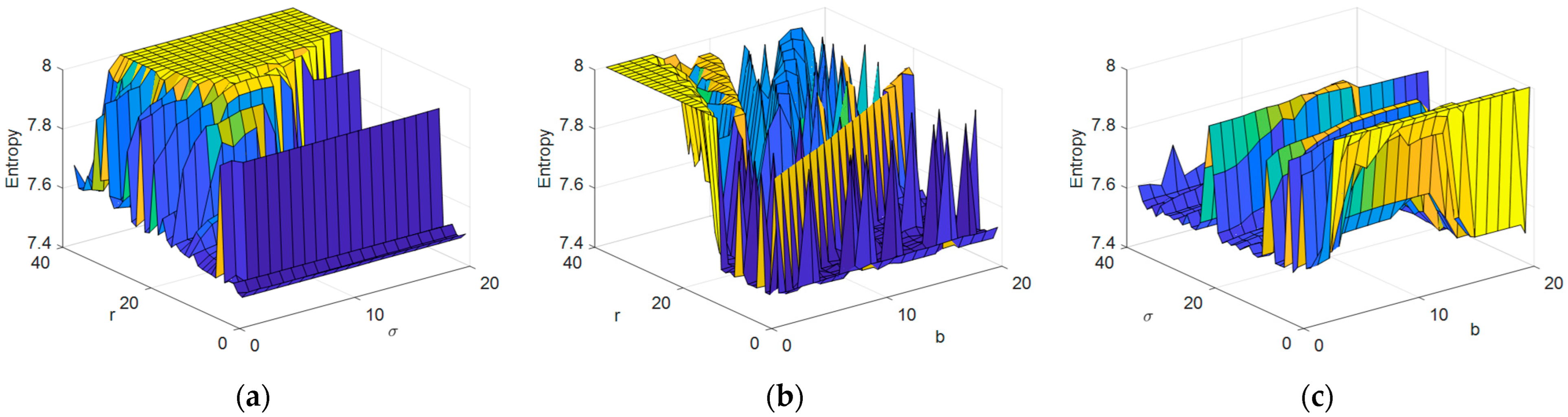
| Entropy | Correlation | |
|---|---|---|
| Input image | 7.3283 | 0.9864 |
| Encrypted image | 7.9973 | −0.0037 |
| Entropy of the Original Image | With Nominal Parameters of the Chaotic System | With Standard Price Optimization Method | With AI-Enhanced Price Optimization Method | |
|---|---|---|---|---|
 | 7.3283 | 7.9975 | 7.9978 = 11.5682 r = 28.8351 | 7.9979 = 12.5817 r = 31.1784 |
 | 7.6968 | 7.9971 | 7.9978 = 11.3439 r = 29.1481 | 7.9981 = 11.8787 r = 29.1722 |
 | 7.7211 | 7.9976 | 7.9978 = 10.0268 r = 28.8655 | 7.9979 = 11.4699 r = 31.1835 |
 | 7.0839 | 7.9972 | 7.9976 = 10.6537 r = 28.4883 | 7.9979 = 11.9907 r = 28.7076 |
 | 7.4868 | 7.9961 | 7.9972 = 11.8724 r = 30.9686 | 7.9974 12.0712 r = 31.0978 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stoycheva, H.; Mihalev, G. Entropy-Based Optimization in Chaotic Image Encryption Algorithms with Implementation of Artificial Intelligence. Eng. Proc. 2025, 104, 16. https://doi.org/10.3390/engproc2025104016
Stoycheva H, Mihalev G. Entropy-Based Optimization in Chaotic Image Encryption Algorithms with Implementation of Artificial Intelligence. Engineering Proceedings. 2025; 104(1):16. https://doi.org/10.3390/engproc2025104016
Chicago/Turabian StyleStoycheva, Hristina, and Georgi Mihalev. 2025. "Entropy-Based Optimization in Chaotic Image Encryption Algorithms with Implementation of Artificial Intelligence" Engineering Proceedings 104, no. 1: 16. https://doi.org/10.3390/engproc2025104016
APA StyleStoycheva, H., & Mihalev, G. (2025). Entropy-Based Optimization in Chaotic Image Encryption Algorithms with Implementation of Artificial Intelligence. Engineering Proceedings, 104(1), 16. https://doi.org/10.3390/engproc2025104016







