PV Power Generation Forecasting with Fuzzy Inference Systems ^†

Abstract

This paper aims to implement a fuzzy system for the purpose of forecasting the output of photovoltaic (PV) systems. A bibliometric review was conducted to establish a baseline, involving the exploration of six different configuration of fuzzy systems. These systems were trained and evaluated using a sliding window technique and a validation set. The development of the study utilized data collected from 1 May 2018 to 30 June 2018 at the Universidad Autónoma de Occidente campus. The dataset was analyzed in order to identify any discernible trends, seasonal patterns, and instances of stationarity. A comparison of the six models revealed their ability to predict PV power generation, with the model with 13 lags and five fuzzy sets demonstrating results with a reasonable trade-off between training and test performance. The model achieved an R-squared value of 0.8124 and an RMSE of 29.7025 kWh in the test data, indicating that the predictions were closely aligned with the actual values. However, this suggests that the model may be overly simple or may require additional data to more accurately capture the inherent variability of the data. The paper concludes with a discussion of the model’s limitations and potential avenues for future research.

1. Introduction

The solar industry in Latin America is demonstrating a promising growth trajectory, with projections indicating an average increase of between 10% and 15% in installed capacity per country by 2025, a trend that is consistent with the current year. According to Sergio Rodríguez, a service manager at Solis, one of the world’s largest manufacturers of photovoltaic inverters, this growth is driven by the increasing demand for clean and sustainable energy in the region. This growth is driven by the increasing demand for clean and sustainable energy in the region, which has positioned countries like Brazil, Mexico, Chile, and Colombia as leaders in solar power production. Brazil leads the way with 45 gigawatts (GW), followed by Mexico with 3.3 GW, Chile with 3 GW, and Colombia with 1.9 GW. This trend highlights the potential of photovoltaic energy in Latin America and underscores the importance of innovating in forecasting technologies to optimize their use [1].

The generation of electricity from solar power is subject to several challenges, with the primary one being the inherently unpredictable nature of solar resources. The quantity of solar energy generated is significantly influenced by the prevailing weather conditions and seasonal fluctuations. Furthermore, several other factors, including panel orientation, tilt angles, equipment efficiency, and maintenance, also have an impact on the output of photovoltaic energy. These complexities make accurate predictions of solar energy generation challenging, which in turn affects the profitability and efficiency of solar energy production.

Consequently, precise forecasting models are crucial for accurate estimation of photovoltaic energy generation. Artificial intelligence techniques have emerged as invaluable tools in this domain, leveraging their ability to process extensive datasets and uncover intricate patterns essential for predicting future solar power output.

To illustrate this, historical energy generation data from the university went through preprocessing, including data imputation to handle missing values in the time series. Subsequently, a genetic algorithm was created to identify the size of the windows, the number of fuzzy sets, and the number of rules best suited to training and validating a fuzzy inference system and obtain the lowest possible error. The fuzzy inference system with a window size equal to NN, with NN fuzzy sets and NN rules, demonstrated superior performance in forecasting photovoltaic power generation based on the available dataset.

The principal advantages of utilizing a genetic algorithm in this context include its capacity to autonomously optimize system characteristics, obviating the necessity for constant human intervention. Genetic algorithms are particularly efficacious in intricate problems with a multitude of variables and prospective solutions, as is the case in the design of fuzzy inference systems. Moreover, their evolutionary nature enables the identification of globally optimal solutions or solutions that are in close proximity to optimality, thereby enhancing the precision of photovoltaic power generation system forecasting.

The structure of this paper is as follows. The introduction is provided in Section 1. Section 2 offers a brief overview of the theoretical and methodological foundations of photovoltaic (PV) power generation forecasting. The methodology applied in the analysis is discussed in Section 3. Section 4 presents the results and a discussion of the findings. Finally, Section 5 concludes the paper with a summary and final remarks.

Literature Review

A bibliometric analysis revealed that the paper by Ahmed, Sreeram, Mishra, and Arif, ‘A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization’, was the most frequently cited work among all published papers. This paper serves as an important benchmark in the field of power generation forecasting. As a review, it discusses photovoltaic (PV) solar power forecasting techniques and optimization strategies, with a particular focus on the challenges of integrating solar energy into power grids due to fluctuating climate conditions. It examines both traditional statistical and novel machine learning methodologies, evaluating their efficacy and constraints. The review underscores the importance of high-quality data, optimal resolution, and optimization techniques to enhance model performance. The article concludes with recommendations for future research, advocating for the use of advanced methods and comprehensive datasets to enhance forecasting accuracy in solar power generation [2].

Another significant benchmark was identified in ‘Multiobjective Intelligent Energy Management for a Microgrid’, authored by Chaouachi, Kamel, Andoulsi, and Nagasaka. This paper proposes the implementation of an intelligent energy management system for a microgrid, employing artificial intelligence techniques and multiobjective linear programming. The system’s aim is to minimize operational costs and environmental impact by considering factors such as the availability of renewable energy sources and load demand. An ensemble of artificial neural networks is employed for the purpose of predicting 24-h photovoltaic generation, one-hour wind power generation, and load demand. A fuzzy logic expert system is utilized for battery scheduling, thereby addressing uncertainties inherent to microgrid operations. The results demonstrated a notable reduction in operational costs and emissions when compared with existing microgrid energy management strategies [3].

In an alternative approach, the paper entitled ‘Deep Learning Using Genetic Algorithm Optimization for Short Term Solar Irradiance Forecasting’ by Bendali, Saber, Bourachdi, Boussetta, and Mourad presents a different perspective. The objective of this paper was to enhance forecasting models for photovoltaic energy production by introducing novel hybrid methodologies that optimize deep learning through a genetic algorithm-based deep neural network. The model forecasts solar irradiation output and compares the performance of three neural networks: long short-term memory (LSTM), a gated recurrent unit (GRU), and a recurrent neural network (RNN). A genetic algorithm (GA) was employed to identify the optimal window size and the most appropriate number of units (neurons) in each as well as all three hidden layers [4].

Moreover, a genetic algorithm (GA) has been used as a learning method to improve the prediction of PV energy by optimizing parameters such as the number of hidden layers and neurons in the ANN model [5]. Additionally, other genetic algorithms, such as the multi-objective non-dominated sorting genetic algorithm, have also been employed [6].

Furthermore, various fuzzy systems have been explored, including a hybrid ANN/GA/ANFIS model [7], Fuzzy-RBF-CNN model [8], and a fuzzy C-means (FCM) algorithm for clustering historical data based on meteorological variables [9]. Fuzzy C-means clustering (FCM) has also been used to create datasets of historically similar days [10]. Additionally, one study utilized an adaptive neural fuzzy inference system (ANFIS) to train and learn from input data for generating output predictions. The training process is further enhanced by employing the particle swarm optimization (PSO) algorithm to optimize ANFIS parameters, thus reducing prediction errors [11].

2. Background

The generation of photovoltaic power faces significant challenges, primarily due to the high degree of uncertainty that is introduced by solar fluctuations, which are influenced by a number of factors, including seasonal and weather conditions. Furthermore, additional factors, including panel tilt, orientation, efficiency, and maintenance, also influence energy production.

To address these challenges, an artificial intelligence model is proposed to predict the energy generation of the photovoltaic system at Universidad Autónoma de Occidente. A genetic algorithm was designed to determine the optimal parameters of the fuzzy inference systems implemented, thus reducing the prediction error.

2.1. Fuzzy System

In the 1960s, Professor Lotfi Zadeh from the University of California, Berkeley introduced the theory of fuzzy sets, a groundbreaking concept that fundamentally altered the understanding of element membership in a set. In contrast to the binary structure of traditional set theory, which allows for only two possible states (either belonging or not) to be assigned to an element, Zadeh proposed that an element can be assigned a degree of membership in a set that is not necessarily binary. This relationship between an element and its degree of membership is represented by what are known as membership functions.

Building on this idea, the entire theory of sets was reformulated, redefining key concepts such as inclusion, union, and logical operators (like AND and OR) and their properties. In the field of logic, novel alternatives were put forth that transcended traditional logic. When evaluating a proposition, it is no longer dichotomous but rather has a degree of truth that is contingent upon the degree of truth of its premises. Consequently, when fuzzy logic is employed in rule evaluation, all rules whose premises have some degree of truth contribute proportionately to the solution to the problem. In other words, every rule that provides information has some influence on the final outcome [12].

Fuzzy sets are a generalization of classical sets that allow for the representation of uncertainties and imprecisions. Unlike traditional sets, where an element either belongs or does not belong to a set (binary values of zero or one), in fuzzy sets, an element can have a degree of membership that ranges from 0 to 1. This means that an element can partially belong to a set [13].

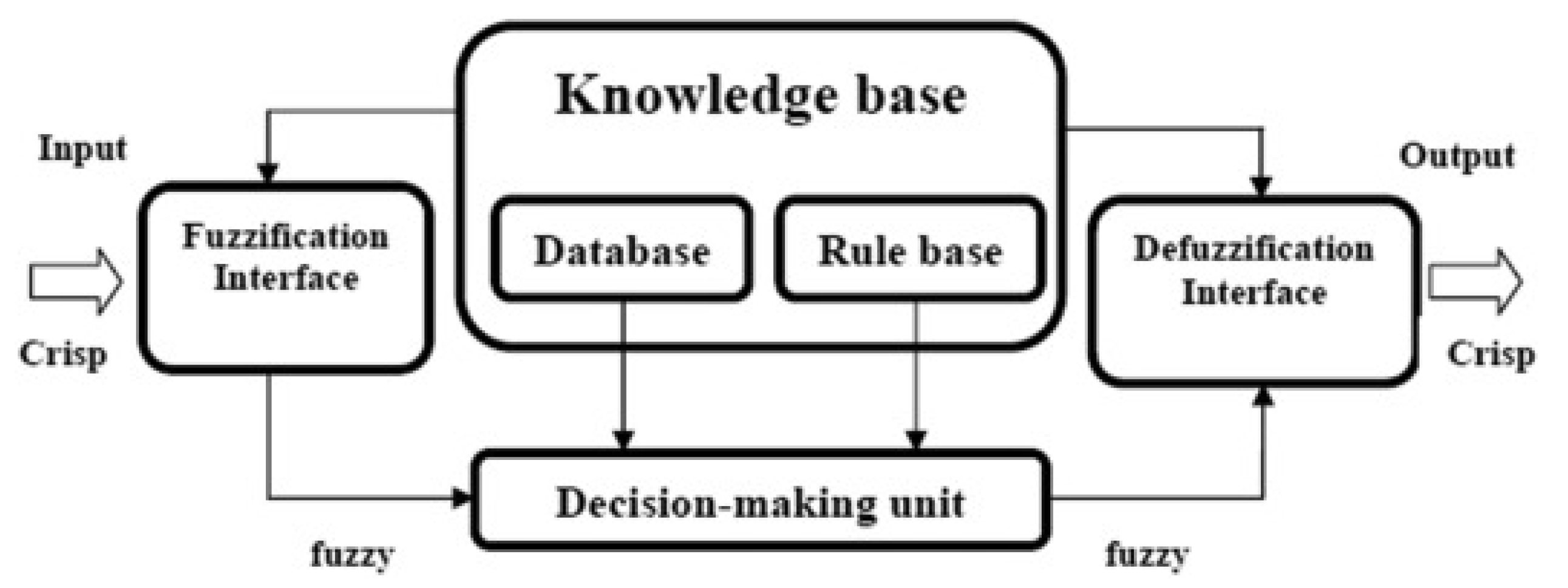
A fuzzy inference system (FIS) consists of five main components (see Figure 1):

• Rule Base: This includes fuzzy IF-THEN rules that define the system’s behavior.
• Database: This defines the fuzzy sets used in the fuzzy rules, which are described by membership functions in the database.
• Decision-Making Unit: This unit performs the inference operation based on the input data and the rules in the base.
• Fuzzification Interface: This unit transforms crisp input values into fuzzy sets, assigning a degree of membership to each linguistic variable.
• Defuzzification Interface: This unit converts the resulting fuzzy sets into a crisp output [14].

Figure 1. Fuzzy inference system’s main components [14].

Figure 1. Fuzzy inference system’s main components [14].

The knowledge base of an FIS consists of the rule base and the database. The fuzzy reasoning process in the FIS involves the following steps:

• Fuzzification of Input: In this step, the input variable is compared with the corresponding membership function. The fuzzy rules are applied to the premise part of the rules to obtain the membership values for each linguistic level.
• Combination of Membership Values: A specific fuzzy T-norm operator (such as multiplication or minimum) is used to combine the membership values and calculate the weight (or firing strength) of each rule.
• Generation of the Consequent: Based on the calculated weight, a qualified consequent is generated, which may be either fuzzy or crisp.
• Defuzzification: In the final step, the qualified consequents are aggregated to produce a crisp output, which is the final result of the fuzzy inference process.

This reasoning process allows the system to make decisions or predictions based on imprecise or uncertain information, using predefined rules and a database of fuzzy sets [14].

The key characteristics of the fuzzy sets are as follows:

• Degree of Membership: Each element in a fuzzy set is associated with a membership value, which indicates the degree to which the element belongs to the set. For example, in a fuzzy set representing ‘tall people’, a person who is 1.80 m tall might have a membership degree of 0.7, while someone who is 1.60 m tall might have a membership degree of 0.3.
• Membership Functions: The relationship between elements and their membership degrees is defined by membership functions. These functions can take various forms, such as triangular, trapezoidal, or Gaussian, and are used to model the smooth transition between different states of membership.
• Operations on Fuzzy Sets: Similar to classical sets, fuzzy sets can be combined using operations like union, intersection, and complement. However, these operations are defined differently, taking into account the membership degrees of the elements.
• Applications: Fuzzy sets are widely used in control systems, artificial intelligence, natural language processing, and any field where uncertainty and imprecision are prevalent. They enable computational systems to mimic human reasoning, which is often not binary [15].

2.2. Genetic Algorithm

A genetic algorithm (GA) is a problem-solving technique inspired by biological evolution used as a strategy for problem resolution, and it is categorized under population-based methods. Given a specific problem to solve, the input for the GA consists of a set of potential solutions encoded in some way and a metric called the fitness function, which allows for the quantitative evaluation of the quality of each candidate solution.

From there, the GA evaluates each candidate based on the fitness function. It is important to note that these initial candidates will likely have low efficiency in solving the problem, and most may not work at all. However, by pure chance, a few may be promising, exhibiting some characteristics that show, albeit weakly and imperfectly, some potential for solving the problem.

These promising candidates are preserved and allowed to reproduce. Multiple copies of them are made, but these copies are not perfect; instead, random changes (mutations) are introduced during the copying process, mimicking the mutations that descendants in a biological population might undergo. The digital offspring then proceed to the next generation, forming a new set of candidate solutions, and they are again subjected to an evaluation round for fitness. Candidates that have worsened or not improved with mutations are discarded. However, again, by pure chance, the random variations introduced into the population might have improved some individuals, making them better solutions to the problem, being more complete or efficient. This process repeats for as many iterations as needed until sufficiently good solutions are found for our purposes. The evolutionary process can be enhanced by allowing the individual characteristics of solutions to combine through crossover operations, simulating sexual reproduction [16].

3. Methodology

This work was developed in the following stages:

3.1. Exploratory Analysis and Data Preprocessing

3.1.1. Dataset Description

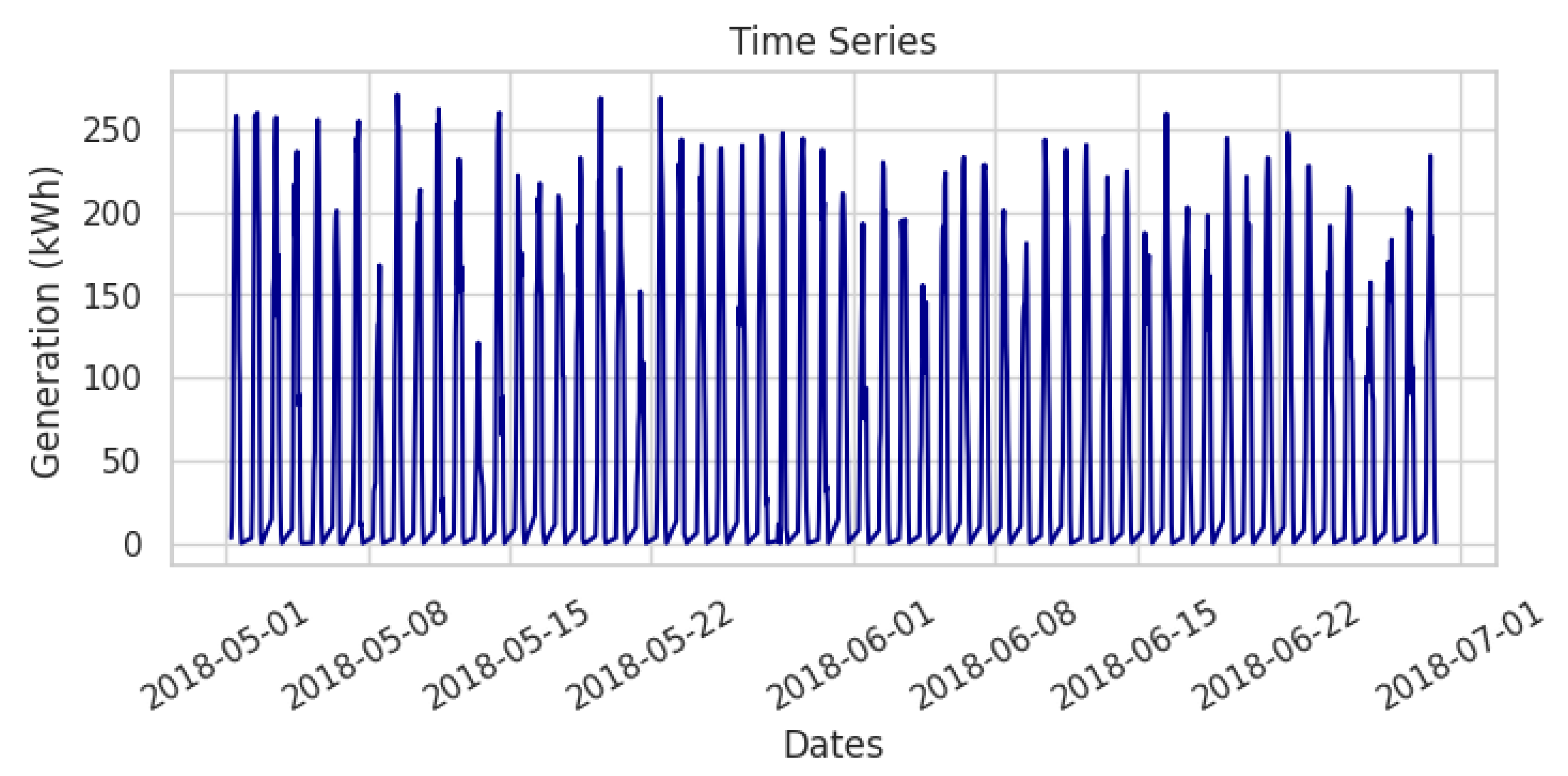
The PV power generation data (in kWh) is provided for the period from 1 May 2018 to 30 June 2018, with hourly intervals from 6:00 a.m. to 6:00 p.m. This timeframe reflects the significant generation patterns observed in Colombia, where sunrise typically occurs around 6:00 a.m. and sunset typically occurs around 6:00 p.m., with minor variations throughout the year, resulting in 13 daily data points (see Figure 2).

3.1.2. Time Series Decomposition

The time series decomposition revealed a high variability caused by weather conditions and other external factors, which made the series susceptible to noise (see Figure 3).

3.1.3. Stationarity Detection

The stationarity detection was performed using the augmented Dickey–Fuller (ADF) test, which rejected the null hypothesis and suggested the absence of a unit root, with a test statistic of −7.979. It is important to note that the strength of the rejection of the null hypothesis increases as the test value becomes more negative. In this case, although the null hypothesis was rejected, the degree of rejection was not substantial. Therefore, while the hypothesis was rejected, additional analysis is necessary to further confirm the stationarity of the time series. To support the claim of stationarity, a p value close to zero was obtained, indicating that it was less than 0.05, which confirmed the time series’ stationarity.

3.1.4. Data Seasonality

Upon analysis of the time series boxplot, it was also observed that the month and hour of generation information exerted a significant influence on the series’ behavior (see Figure 4).

3.2. Model Training

In order to conduct training and model selection, it was necessary to divide the dataset. Given that two months of generation were used, with each day comprising 13 data points out of the 780 data points, 90% (702) were allocated for training, and 10% (78) were allocated for testing. This approach was adopted in order to avoid overtraining the models.

The training of the fuzzy model requires the creation of terms that can be used for the automatic extraction of rules. In this instance, given that the data set is a time series, the terms will be the values that precede the value to be predicted. This quantity is referred to as the size of the window or lag. Furthermore, the number of fuzzy sets that will be utilized to contain the universe of the time series is defined (for example, as shown in Figure 5 that has 7 fuzzy sets).

Subsequently, the automatic extraction of rules is performed. Initially, a list of fuzzy rules is created from the values of the data frame generated with all lags and the linguistic variables. The membership of each rule entry with respect to the fuzzy sets is calculated, the antecedents and consequents of the rule are created, and the relevance level of the rule is calculated. Additionally, redundant rules are filtered out, which is necessary given the potentially high computational cost associated with building a fuzzy system from a rather large training set.

In this study, the error was calculated using two metrics: the root mean square error (RMSE) and the coefficient of determination (R²). The RMSE was selected because it is sensitive to large errors and provides interpretable units, whereas R² was chosen as a measure of global fit, indicating how well the model fit the data.

4. Results and Discussion

As a baseline, six models were trained by varying the window size and the number of fuzzy sets. The results are detailed in

Table 1. Comparison of the predictive ability of the baseline models.

Models	Lags	Fuzzy Sets	RMSE Train	RMSE Test	R2 Train	R2 Test
Model 1	13	5	31.5239	29.7025	0.8559	0.8124
Model 2	9	5	36.7608	29.9501	0.8036	0.8068
Model 3	6	5	40.8346	38.8661	0.7598	0.6747
Model 4	13	7	17.0711	34.7635	0.9577	0.7367
Model 5	9	7	24.3457	32.0697	0.9138	0.7785
Model 6	6	7	27.7871	31.1185	0.8887	0.7914

. It can be observed that the use of more fuzzy sets resulted in improved results. Additionally, for this data set, the following was found.

Model 1 appears to be the optimal model in terms of generalization, as it exhibited the best performance on the test set with a low test RMSE and a high test R-squared. Model 4 demonstrated an excellent fit with the training data; however, its performance on the test set was not as robust, indicating the possibility of overfitting. Model 3 exhibited the poorest performance overall, with an extremely high test RMSE and a low test R-squared, suggesting that it is not a suitable model for PV generation prediction.

In contrast, Model 5 demonstrated satisfactory overall performance, exhibiting a favorable alignment with the training data and adequate performance on the test data. Although it was not the most optimal model in terms of the test root mean square error (RMSE), it remained competitive, particularly in comparison with Models 3 and 4. The test R-squared value suggests that the model demonstrated satisfactory generalizability, although further optimization through parameter adjustments or the incorporation of additional data may enhance this attribute.

Given the time required to complete each experiment, it was determined that a population-based optimization algorithm would be an effective approach to reduce the training error of the fuzzy inference system. The objective was to identify the optimal number of lags, fuzzy sets, and rules for performing the inference.

The restrictions proposed were based on an analysis of the nature of the problem and the computational cost of training and searching for individuals that offered an optimal solution. Specifically, the number of lags was limited to a range of 6–13, the number of fuzzy sets was set between 3 and 5 or 7, and the number of rules was constrained to a range of 7–13 for the purpose of performing the inference.

The algorithm in question has an initial population of 100 individuals, with 200 iterations established in this case. Furthermore, if a particle does not comply with the restrictions, then it is assigned a penalty of −10.000, thereby reducing the attractiveness of its solution.

A review of the results showed in

Table 2. Comparison of individuals obtained with genetic algorithm.

Models	Lags	Fuzzy Sets	Rules	RMSE Train
Model 1	13	4	7	42.16
Model 2	6	12	4	46.54
Model 3	3	13	13	47.29
Model 4	3	6	4	62.77
Model 5	13	7	13	39.05

indicates that the process generated diverse outcomes with respect to constraint fulfillment. Two individuals exhibited a lag of less than six, one individual satisfied the requisite number of fuzzy sets, and three individuals reached the valid number of rules. However, only one individual comprehensively met all the established constraints, thus representing the only successful case within the evaluated set. These results suggest the possibility of adjusting the design of the process, whereby increasing the number of iterations and applying a higher penalty in the genetic algorithm could be an effective strategy for generating individuals that meet the constraints more consistently and improving the overall performance of the system.

5. Conclusions

Analyzing and decomposing time series data is crucial when choosing the right models to implement. The decomposition of the time series provided a clear view of the seasonality in daily energy generation and uncovered notable patterns over time. Furthermore, the box plot highlights significant variability and fluctuations in the data, which can be linked to the influence of weather conditions on solar irradiance.

The fuzzy models demonstrated an effective ability to predict the data, with varying degrees of success depending on the configuration of lags and fuzzy sets. In general, the performance of the models improved with the appropriate combination of these parameters. Model 1 stood out as the best model overall, showing strong generalization capabilities, with a low RMSE on both the training and test sets and a high R-squared value on the test set, indicating accurate predictions and good alignment with real values.

On the other hand, Model 4, despite having the best training RMSE and R-squared value, suffered from a lower R-squared value on the test set, suggesting potential overfitting to the training data. Model 5 also performed well, showing competitive results with a reasonable trade-off between training and test performance. The relatively good R-squared values on the test set suggest that Model 5 had a solid ability to generalize, even though it was not the top performer.

In contrast, Model 3 showed the weakest performance, with a high RMSE and low R-squared value on both the training and test sets, indicating that its configuration was not suitable for accurately predicting the data.

In regard to the genetic algorithm, it can be stated that a single individual fully satisfied all the established constraints, thereby representing the only successful case within the evaluated set. It is noteworthy that this valid individual closely resembled the one with the best performance when the fuzzy inference system was applied. These results suggest the potential for improving the process design by increasing the number of iterations and implementing a higher penalty within the genetic algorithm.

The data set used in this study, comprising 780 points related to two months of records, is sufficiently extensive to permit the capture of variations in photovoltaic (PV) generation. Nevertheless, the utilization of substantial data volumes and parameter optimization increased the computational expense and training period, particularly when employing optimization algorithms such as particle-based optimization. To address this issue, it is essential to employ efficient optimization algorithms that enhance model performance without exceeding the available resources.

The bibliometric analysis highlighted several key contributions to PV solar power forecasting, emphasizing the importance of advanced techniques for improved accuracy. The use of AI, genetic algorithms, and fuzzy systems has proven effective in optimizing models for PV energy production. Hybrid approaches that combine these methods, along with the integration of high-quality data and optimization strategies, significantly enhance the performance of forecasting models. These advancements suggest that future efforts should focus on refining these techniques and utilizing comprehensive datasets to further improve the accuracy and reliability of solar power predictions.

Moreover, it has been noted that prediction models now include variables with strong correlations, such as irradiance, temperature, and relative humidity, leading to enhanced forecasting accuracy.