Hydrogen Bond Binding of Water to Two Cholic Acid Residues †
Abstract
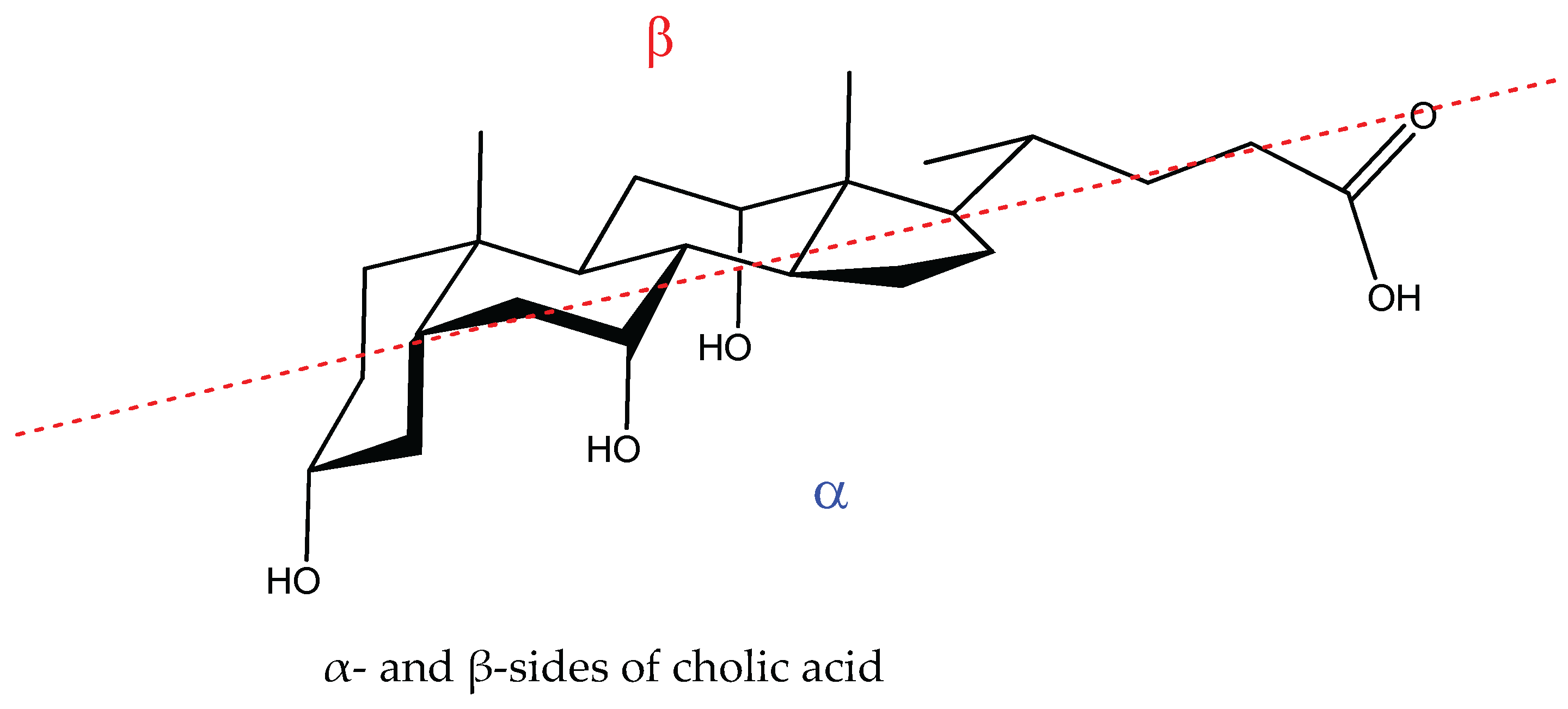
:1. Introduction
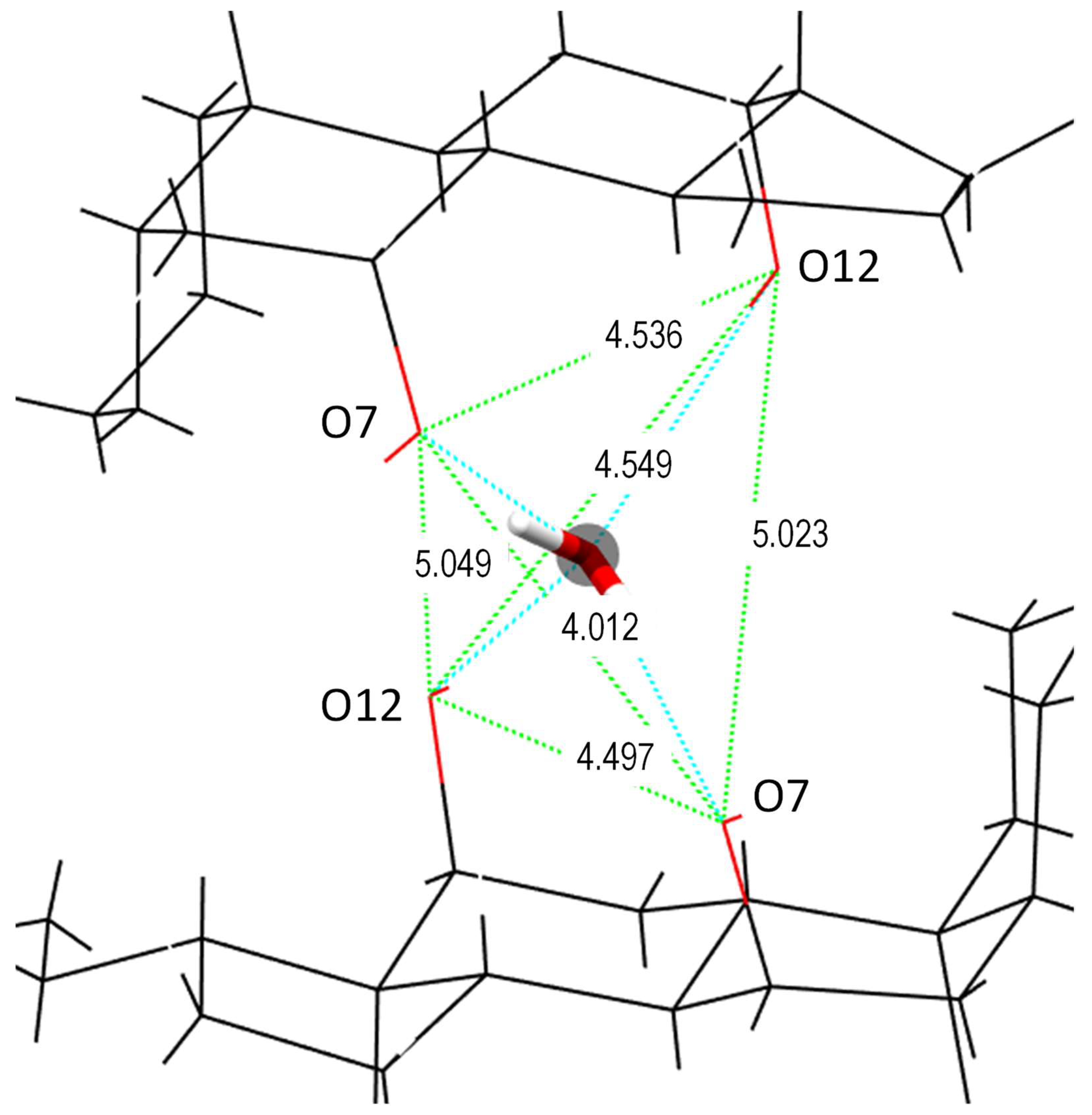
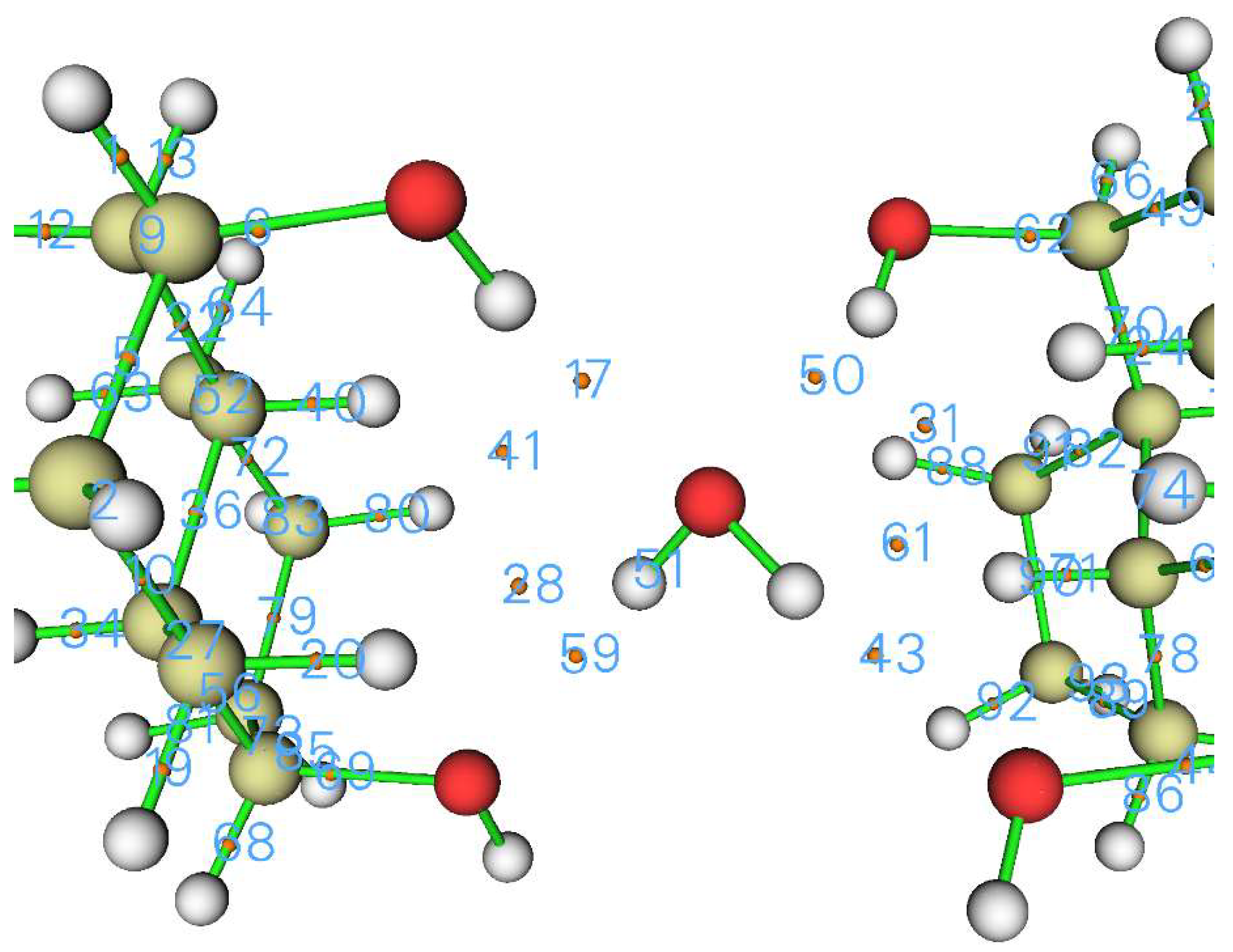
2. Crystal Structure
2.1. Computational Details
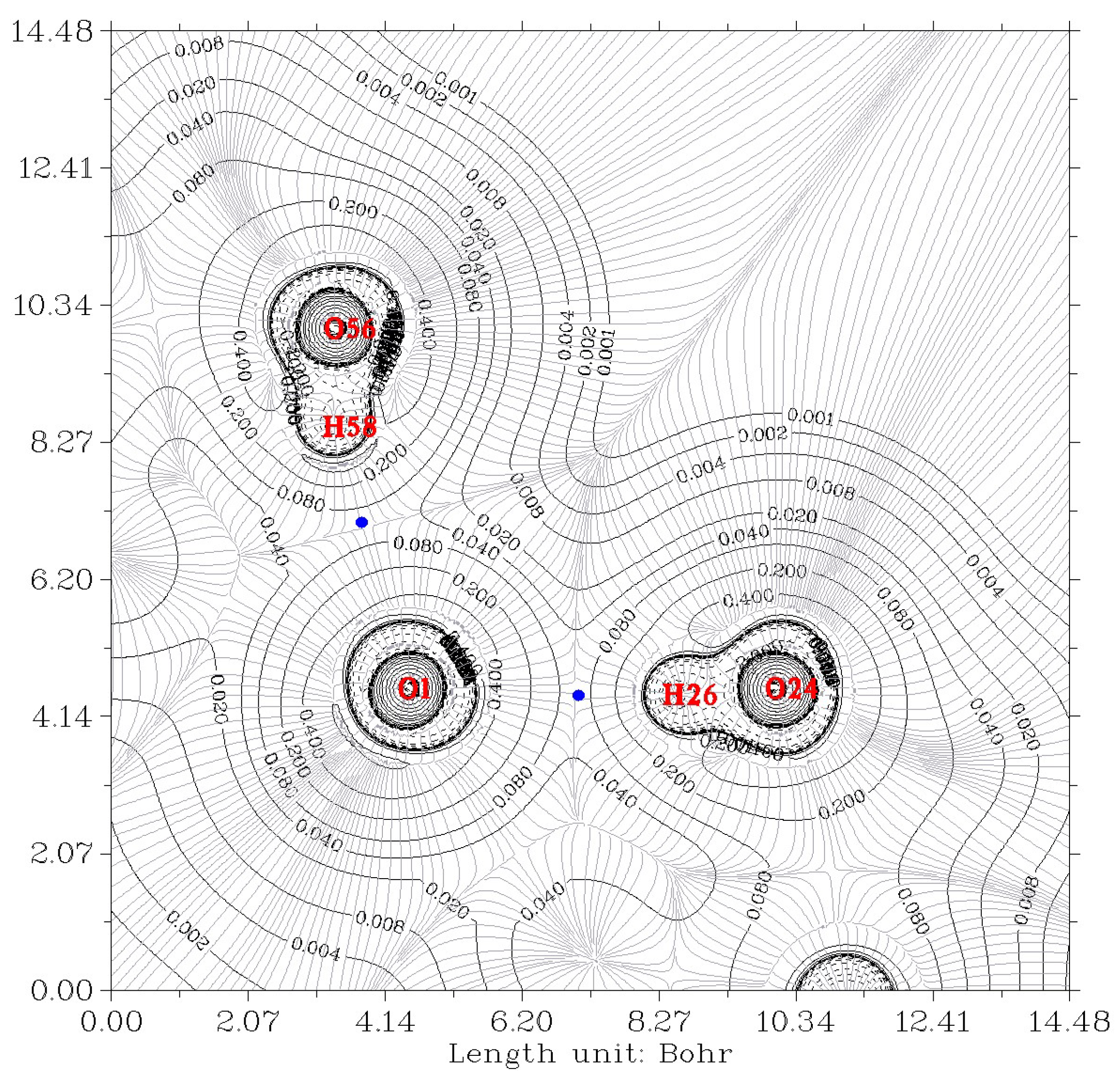
2.2. Analysis of Electron Density
2.3. Energy of Hydrogen Bonds
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meijide, F.; de Frutos, S.; Soto, V.H.; Jover, A.; Seijas, J.A.; Vázquez-Tato, M.P.; Fraga, F.; Vázquez Tato, J. A standard structure for bile acids and derivatives. Crystals 2018, 8, 86. [Google Scholar] [CrossRef]
- Giglio, E. Structural aspect of inclusion compounds formed by organic host lattices. In Inclusion Compounds of Deoxycholic Acid; Atwood, J.L., Davies, J.E.D., MacNicol, D.D., Eds.; Academic Press: London, UK, 1984; pp. 207–229. [Google Scholar]
- Miyata, M.; Sada, K. Deoxycholic acid and related hosts. In Comprehensive Supramolecular Chemistry; MacNicol, D.D., Bishop, R.T.F., Eds.; Elsevier: Oxford, UK, 1996; Volume 6, pp. 147–176. [Google Scholar]
- Campanelli, A.R.; Candeloro de Sanctis, S.; Giglio, E.; Viorel Pavel, N.; Quagliata, C. From crystal to micelle: A new approach to the micellar structure. J. Incl. Phenom. Macrocyclic. Chem. 1989, 7, 391–400. [Google Scholar] [CrossRef]
- Sada, K.; Sugahara, M.; Kato, K.; Miyata, M. Controlled Expansion of a Molecular Cavity in a Steroid Host Compound. J. Am. Chem. Soc. 2001, 123, 4386–4392. [Google Scholar] [CrossRef] [PubMed]
- Sugahara, M.; Sada, K.; Miyata, M. A robust structural motif in inclusion crystals of nor-bile acids. Chem. Commun. 1999, 3, 293–294. [Google Scholar] [CrossRef]
- Sugahara, M.; Sada, K.; Hirose, J.; Miyata, M. Inclusion abilities of bile acids with different side chain length. Mol. Cryst. Liquid Cryst. 2001, 356, 155–162. [Google Scholar] [CrossRef]
- Hishikawa, Y.; Aoki, Y.; Sada, K.; Miyata, M. Selective inclusion phenomena in lithocholamide crystal lattices; design of bilayered assemblies through ladder-type hydrogen bonding network. Chem. Lett. 1998, 27, 1289–1290. [Google Scholar] [CrossRef]
- Miyata, M.; Tohnai, N.; Hisaki, I. Supramolecular chirality in crystalline assemblies of bile acids and their derivatives; three-axial, tilt, helical, and bundle chirality. Molecules 2007, 12, 1973–2000. [Google Scholar] [CrossRef]
- Miragaya, J.; Jover, A.; Fraga, F.; Meijide, F.; Vázquez Tato, J. Enantioresolution and Chameleonic Mimicry of 2-Butanol with an Adamantylacetyl Derivative of Cholic Acid. Crystal Growth Des. 2010, 10, 1124–1129. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen Bond—Definitions, Criteria of Existence and Various Types. In Understanding Hydrogen Bonds: Theoretical and Experimental Views; Theoretical and Computational Chemistry Series; Royal Society of Chemistry: London, UK, 2020; Chapter 1; pp. 1–40. ISBN 978-1-83916-040-0. [Google Scholar] [CrossRef]
- Popelier, P.L.A. On the full topology of the Laplacian of the electron densityOn the full topology of the Laplacian of the electron density. Coord. Chem. Rev. 2000, 197, 169–189. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Soto, V.H.; Alvarez, M.; Meijide, F.; Trillo, J.V.; Antelo, A.; Jover, A.; Galantini, L.; Vázquez Tato, J. Ice-like encapsulated water by two cholic acid moieties. Steroids 2012, 77, 1228–1232. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, N.H. The Chemical Physics of Ice. In The Chemical Physics of Ice; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Bergmann, U.; Di Cicco, A.; Wernet, P.; Principi, E.; Glatzel, P.; Nilsson, A. Nearest-neighbor oxygen distances in liquid water and ice observed by x-ray Raman based extended x-ray absorption fine structure. J. Chem. Phys. 2007, 127, 174504. [Google Scholar] [CrossRef] [PubMed]
- Steiner, T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 RC; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Popelier, P.L.A. Characterization of a Dihydrogen Bond on the Basis of the Electron Density. J. Phys. Chem. A 1998, 102, 1873–1878. [Google Scholar] [CrossRef]
- Carroll, M.T.; Chang, C.; Bader, R.F.W. Prediction of the structures of hydrogen-bonded complexes using the laplacian of the charge density. Mol. Phys. 1988, 63, 387–405. [Google Scholar] [CrossRef]
- Koch, U.; Popelier, P.L.A. Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. A 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of Atoms in Molecules: Atomic Volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Alkorta, I.; Rozas, I.; Elguero, J. Bond Length–Electron Density Relationships: From Covalent Bonds to Hydrogen Bond Interactions. Struct. Chem. 1998, 9, 243–247. [Google Scholar] [CrossRef]
- Tang, T.-H.; Deretey, E.; Jensen, S.J.K.; Csizmadia, I.G. Hydrogen bonds: Relation between lengths and electron densities at bond critical points. Eur. Phys. J. D 2006, 37, 217–222. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Cole, W.T.; Saykally, R.J. The water dimer I: Experimental characterization. Chem. Phys. Lett. 2015, 633, 13. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Xantheas, S.S.; Saykally, R.J. The water dimer II: Theoretical investigations. Chem. Phys. Lett. 2018, 700, 163–175. [Google Scholar] [CrossRef]
- Dyke, T.R.; Muenter, J.S. Microwave spectrum and structure of hydrogen bonded water dimer. J. Chem. Phys. 1974, 60, 2929. [Google Scholar] [CrossRef]
- Dyke, T.R.; Mack Kenneth, M.; Muenter, J.S. The structure of water dimer from molecular beam electric resonance spectroscopy. J. Chem. Phys. 1977, 66, 498. [Google Scholar] [CrossRef]
- Odutola, J.A.; Dyke, T.R. Partially deuterated water dimers: Microwave spectra and structure. J. Chem. Phys. 1980, 72, 5062. [Google Scholar] [CrossRef]
- Grabowski, S.J. High-Level Ab Initio Calculations of Dihydrogen-Bonded Complexes. J. Phys. Chem. A 2000, 104, 5551–5557. [Google Scholar] [CrossRef]
- Grabowski, S.J. Ab Initio Calculations on Conventional and Unconventional Hydrogen Bonds Study of the Hydrogen Bond Strength. J. Phys. Chem. A 2001, 105, 10739–10746. [Google Scholar] [CrossRef]
- Emamian, S.; Lu, T.; Kruse, H.; Emamian, H. Exploring Nature and Predicting Strength of Hydrogen Bonds: A Correlation Analysis Between Atoms-in-Molecules Descriptors, Binding Energies, and Energy Components of Symmetry-Adapted Perturbation Theory. J. Comput. Chem. 2019, 40, 2868–2881. [Google Scholar] [CrossRef]
- Gu, Y.; Kar, T.; Scheiner, S. Fundamental Properties of the CH···O Interaction: Is It a True Hydrogen Bond? J. Am. Chem. Soc. 1999, 121, 9411–9422. [Google Scholar] [CrossRef]
- Kumar, P.S.V.; Raghavendra, V.; Subramanian, V. Bader’s Theory of Atoms in Molecules (AIM) and its Applications to Chemical Bonding. J. Chem. Sci. 2016, 128, 1527–1536. [Google Scholar] [CrossRef]
- Isaev, A.N. Ammonia and phosphine complexes with proton donors. Hydrogen bonding from the backside of the N(P) lone pair. Comp. Theor. Chem. 2018, 1142, 28–38. [Google Scholar] [CrossRef]
- Rowland, R.S.; Taylor, R. Intermolecular nonbonded contact distances in organic crystal structures: Comparison with distances expected from van der Waals radii. J. Phys. Chem. 1996, 100, 7384–7391. [Google Scholar] [CrossRef]
- Jeffrey, G.J. An Introduction to Hydrogen Bonding; Oxford University Press: New York, NY, USA, 1997; p. 12. [Google Scholar]
- Ruscic, B. Active Thermochemical Tables: Water and Water Dimer. J. Phys. Chem. A 2013, 117, 11940–11953. [Google Scholar] [CrossRef] [PubMed]
- Feyereisen, M.W.; Feller, D.; Dixon, D.A. Hydrogen Bond Energy of the Water Dimer. J. Phys. Chem. 1996, 100, 2993–2997. [Google Scholar] [CrossRef]
- Rocher-Casterline, B.E.; Ch’ng, L.C.; Mollner, A.K.; Reisler, H. Communication: Determination of the Bond Dissociation Energy (Do) of the Water Dimer, (H2O)2, by Velocity Map Imaging. J. Chem. Phys. 2011, 134, 211101. [Google Scholar] [CrossRef] [PubMed]
- Shank, A.; Wang, Y.; Kaledin, A.; Braams, B.; Bowman, J. Accurate ab initio and "hybrid" potential energy surfaces, intramolecular vibrational energies, and classical ir spectrum of the water dimer. J. Chem. Phys. 2009, 130, 144314. [Google Scholar] [CrossRef]
- Moin, S.T.; Hofer, T.S.; Randolf, B.R.; Rode, B.M. Structure and dynamics of methanol in water: A quantum mechanical charge field molecular dynamics study. J. Comput. Chem. 2011, 32, 886–892. [Google Scholar] [CrossRef]
- Boyd, R.J.; Choi, S.C. Hydrogen bonding between nitriles and hydrogen halides and the topological properties of molecular charge distributions. Chem. Phys. Lett. 1986, 129, 62–65. [Google Scholar] [CrossRef]
- Rozenberg, M. The hydrogen bond-practice and QTAIM theory. RSC Adv. 2014, 4, 26928–26931. [Google Scholar] [CrossRef]
- Ghanty, T.K.; Staroverov, V.N.; Koren, P.R.; Davidson, E.R. Is the Hydrogen Bond in Water Dimer and Ice Covalent? J. Am. Chem. Soc. 2000, 122, 1210–1214. [Google Scholar] [CrossRef]

| Oxygen of Water Is Donor | Oxygen of Water Is Acceptor | |||
|---|---|---|---|---|
| Ow-H...O7 | O12-H...Ow | |||
| O–O distance/Å | 2.710 | 2.738 | 2.935 | 2.936 |
| Oxygen of Water Is Donor | Oxygen of Water Is Acceptor | |||
|---|---|---|---|---|
| Property at HBCP | Ow-H…O7 | Ow-H…O7 | O12-H…Ow | O12-H… Ow |
| CP43 | CP59 | CP17 | CP50 | |
| a O–O length/Å crystal | 2.710 | 2.738 | 2.935 | 2.936 |
| a O…H length/Å crystal | 1.866 | 1.920 | 2.177 | 2.114 |
| Electron density ρb (au) | 0.0270 | 0.0239 | 0.0138 | 0.0154 |
| ρb (au) calculated from eq of Ref. [25] (see text) | 0.0307 | 0.0270 | 0.0145 | 0.0170 |
| Laplacian of the electron density at HBCP, ∇2ρb (au) | 0.118 | 0.106 | 0.0616 | 0.0667 |
| HBCP…O length/Å, r1 | 1.217 | 1.242 | 1.383 | 1.355 |
| HBCP…H length/Å, r2 | 0.650 | 0.679 | 0.795 | 0.759 |
| r1 + r2 = O…H length/Å | 1.867 | 1.921 | 2.178 | 2.114 |
| /Å | 0.363 | 0.338 | 0.197 | 0.225 |
| 0.450 | 0.421 | 0.305 | 0.341 | |
| ρb (au) | ∇2ρb | rH…Y/Å | EHB, kcal/mol | Ref. |
|---|---|---|---|---|
| 0.0199 | 0.0624 | −5.5 | [23] | |
| 1.949 | −4.45 | [31] | ||
| 1.825 | −10.97 | [31] | ||
| 0.023 | 0.091 | 1.950 | −4.45 | [32] |
| 0.017 | 0.075 | 2.056 | −4.25 | [32] |
| 0.0259 | −4.93 | [33] | ||
| −4.96 | [33] | |||
| −4.32 ± 0.31 | [34] | |||
| 0.0219 | 0.0396 | 1.949 | −4.33 | [35] |
| HBCP | 17 | 43 | 50 | 59 | Total 4 HB | H–OH…OH2 |
|---|---|---|---|---|---|---|
| /kcal mol−1 Equation (1) [45] | −2.430 | −6.263 | −2.895 | −5.363 | −16.951 | −4.201 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez-Tato, M.P.; Seijas, J.A.; Meijide, F.; de Frutos, S.; Tato, J.V. Hydrogen Bond Binding of Water to Two Cholic Acid Residues. Chem. Proc. 2022, 12, 95. https://doi.org/10.3390/ecsoc-26-13555
Vázquez-Tato MP, Seijas JA, Meijide F, de Frutos S, Tato JV. Hydrogen Bond Binding of Water to Two Cholic Acid Residues. Chemistry Proceedings. 2022; 12(1):95. https://doi.org/10.3390/ecsoc-26-13555
Chicago/Turabian StyleVázquez-Tato, María Pilar, Julio A. Seijas, Francisco Meijide, Santiago de Frutos, and José Vázquez Tato. 2022. "Hydrogen Bond Binding of Water to Two Cholic Acid Residues" Chemistry Proceedings 12, no. 1: 95. https://doi.org/10.3390/ecsoc-26-13555
APA StyleVázquez-Tato, M. P., Seijas, J. A., Meijide, F., de Frutos, S., & Tato, J. V. (2022). Hydrogen Bond Binding of Water to Two Cholic Acid Residues. Chemistry Proceedings, 12(1), 95. https://doi.org/10.3390/ecsoc-26-13555







