Simulation of Oxygen Diffusion in Lead–Bismuth Eutectic for Gas-Phase Oxygen Management

Abstract

Lead–bismuth eutectic (LBE), while advantageous for advanced nuclear reactors due to its thermophysical properties, faces oxidation and corrosion challenges during operation. This study aims to optimize gas-phase oxygen control by computationally analyzing oxygen transport dynamics in an LBE loop. High-fidelity simulations were performed using ANSYS Fluent and STAR-CCM+ based on the CORRIDA loop geometry, employing detailed meshing for convergence. Steady-state analyses revealed localized oxygen enrichment near the gas–liquid interface (peaking at ∼$3\times {10}^{-6}$ wt%), decreasing to ∼$5.0-6.8\times {10}^{-8}$ wt% at the outlet. Transient simulations from an oxygen-deficient state ($1\times {10}^{-8}$ wt%) demonstrated distribution stabilization within 150 s, driven by convection-enhanced diffusion. Parametric studies identified a non-monotonic relationship between inlet velocity and oxygen uptake, with optimal performance at 0.7–0.9 m/s, while increasing temperature from 573 K to 823 K monotonically enhanced the outlet concentration by >$200\%$ due to improved diffusivity/solubility. The average mass transfer coefficient (0.6–0.7) aligned with literature values ($\pm 20\%$ deviation), validating the model’s treatment of interface thermodynamics and turbulence. These findings the advance mechanistic understanding of oxygen transport in LBE and directly inform the design of oxygenation systems and corrosion mitigation strategies for liquid metal-cooled reactors.

1. Introduction

Lead–bismuth eutectic (LBE) has attracted sustained interest as a coolant for advanced nuclear systems owing to its high boiling point, good neutronic transparency, and chemical stability under controlled oxygen conditions [1]. Its favorable thermophysical properties support compact designs in nuclear engineering, yet corrosion and oxidation remain critical challenges when dissolved oxygen is not properly managed [2,3]. Uncontrolled oxidation can generate dense lead and bismuth oxides that impair heat transfer surfaces and accelerate material degradation. Consequently, a quantitative understanding of oxygen diffusion and its coupling with flow and interface thermodynamics is essential for achieving reliable oxygen control in LBE loops.

Prior research has explored alloying and surface treatment strategies to form protective oxide layers [4,5]. However, maintaining oxygen in the narrow window that prevents both aggressive corrosion (too low $C_O$) and oxide precipitation (too high $C_O$) requires robust predictive models of oxygen transport.

Among various approaches, computational fluid dynamics (CFD) offers spatially resolved insight into convection-enhanced diffusion. The work by Wang et al. [6] provided a foundational analysis of oxygen control, evaluating inlet oxygen level, interface concentration, mass flow rate, and temperature, and produced a correlation decoupling temperature and velocity effects.

Arkundato [7] studied iron corrosion resistance via molecular dynamics; Tan [8] introduced a cellular automaton oxidation model; Ito [9] developed COCOA for oxygen control (with PID (Proportional–Integral–Derivative) regulation outperforming ON-OFF); Wang [10] characterized ODS austenitic steels in oxygen-saturated LBE; Chen [11] employed lattice Boltzmann corrosion transport modeling; Ye [12] identified an IOZ (Internal Oxidation Zone) beneath duplex oxides; Ma [13] examined the fluid movement and oxygen transfer in a rectangular container under different temperature boundary conditions; Vigier [14] analyzed MOX fuel interaction; Wang [15] investigated weld joint oxidation heterogeneity; Okubo [16] assessed irradiation-driven oxide layer formation; and Chen [17] explored forced convection oxygen transfer and cover gas mixing challenges. This body of work establishes the sensitivity of corrosion mitigation to accurate oxygen profiling.

In addition, experimental efforts (e.g., Liang [18]) quantified the dissolution kinetics of solid PbO mass exchangers for active oxygen control, demonstrating high-precision regulation capability.

Existing CFD studies rarely combine (i) explicit thermodynamic equilibrium coupling at the gas–liquid interface, (ii) dual-solver cross-validation, and (iii) transient parametric optimization identifying a velocity window for maximal uptake. This work addresses these gaps by simulating oxygen transport in a scaled CORRIDA-based device, quantifying mass transfer coefficient sensitivity to flow rate and temperature, and clarifying equilibrium concentration impacts. We further refine grid independence criteria and introduce additional diagnostics (interfacial flux integral) to strengthen validation.

2. Materials and Methods

2.1. Oxygen Diffusion Models

The transport of dissolved oxygen within the turbulent LBE flow is governed by the convection–diffusion equation. This fundamental relationship, which accounts for both temporal and spatial changes in oxygen concentration, is expressed as follows:

$${\displaystyle \frac{\partial C}{\partial t}}+\overrightarrow{u}·\nabla C=\nabla ·\left(D+{\displaystyle \frac{{\nu }_t}{S_{C_t}}}\right)\nabla C+q_o$$

(1)

where C is the local oxygen concentration and $\overrightarrow{u}$ represents the velocity vector of the fluid. The term combining the molecular diffusion coefficient (D) and the turbulent diffusivity is often referred to as the effective diffusivity, $D_{eff}=D+{\nu }_t/S_{C_t}$. The turbulent diffusivity component is derived from the turbulent kinematic viscosity (${\nu }_t$) and the turbulent Schmidt number ($S_{C_t}$). The source term, $q_o$, accounts for any oxygen supplied by external sources, such as a cover gas system or an oxygen control device.

For the specific case of one-dimensional diffusion into a stationary medium with a constant surface concentration, Equation (1) simplifies to Fick’s second law. We consider a slab of thickness l (characteristic diffusion depth) with initial uniform concentration $C(x,0)=C_0$ and boundary $C(0,t)=C_s$, ${\partial C/\partial x|}_{x=l}=0$ (semi-infinite approximation if $l\to \infty$). The analytical series solution applies under these conditions [19].

$${\displaystyle \frac{\partial C}{\partial t}}=D{\displaystyle \frac{{\partial }^{2}C}{\partial x^2}}$$

(2)

An analytical solution for this scenario (referenced to Crank’s The Mathematics of Diffusion [19]) describes the cumulative mass uptake over time. The ratio of oxygen absorbed at time t, denoted as $M_t$, to the total amount absorbed at saturation, $M_{\infty }$, is given by

$${\displaystyle \frac{M_t}{M_{\infty }}}=1-{\displaystyle \frac{8}{{\pi }^2}}\sum _{n=0}^{\infty }{\displaystyle \frac{1}{{(2n+1)}^2}}exp\left(-{(2n+1)}^2{\pi }^2{\displaystyle \frac{Dt}{l^2}}\right)$$

(3)

where l is the characteristic length (m) representing the diffusion penetration depth, which serves as the characteristic scale in the dimensionless time parameter $Dt/l^2$.

The accuracy of the transport model is critically dependent on the thermophysical properties of oxygen in LBE. This study adopts the widely accepted empirical correlations for the diffusion coefficient ($D_o$) and solubility (S) as proposed by Fazio et al. [20]. Here, $D_o$ denotes the molecular diffusion coefficient of oxygen in LBE, which corresponds to the species-specific realization of the general diffusion coefficient D appearing in Equation (1). The subscript “o” explicitly indicates oxygen as the diffusing species. All temperatures are in Kelvin and correlations are consistently converted to SI units for implementation.

$$\begin{array}{cc}{D}_o\left({\mathrm{cm}}^2/\mathrm{s}\right)=0.0239e^{-{\displaystyle \frac{43073}{RT}}}\hfill & \hfill 473\mathrm{K}<T<1273\mathrm{K}\\ log(S,wt\%)=2.52-4803/T\hfill & 473\mathrm{K}<T<923\mathrm{K}\hfill \end{array}$$

(4)

In Equation (4), $D_o$ is the molecular diffusion coefficient of oxygen in LBE, R is the universal gas constant (8.314 J·K⁻¹·mol⁻¹), T is the absolute temperature (K), and S is the oxygen solubility in LBE (wt%).

To quantify the overall rate of oxygen transfer from the gas–liquid interface into the bulk fluid, the mean mass transfer coefficient, K, is calculated. This coefficient normalizes the net mass flux by the concentration driving force, as defined in the following expression:

$$K={\displaystyle \frac{\dot{m}(C_{\mathrm{out}}-C_{\mathrm{in}})}{A\left(C_s-\frac{C_{\mathrm{in}}+C_{\mathrm{out}}}{2}\right)}}$$

(5)

where $\dot{m}$ is the mass flow rate of LBE (kg s⁻¹), A is the surface area of the gas–liquid interface (m²), $C_{\mathrm{in}}$ and $C_{\mathrm{out}}$ are the oxygen concentrations (wt%) at the inlet and outlet, respectively, and $C_s$ represents the oxygen concentration at the interface. The denominator uses the arithmetic mean $(C_{\mathrm{in}}+C_{\mathrm{out}})/2$ to represent the average bulk concentration, eliminating the need for an additional symbol.

2.2. Geometry and Boundary Conditions

2.2.1. Geometry Description

The CORRIDA loop, depicted in Figure 1a, is a dual-loop experimental facility designed to study oxygen control in liquid lead–bismuth eutectic (LBE) coolants for nuclear reactor applications [21]. The facility comprises two separate circulation loops: (i) a primary LBE circulation loop equipped with an electromagnetic pump to maintain continuous flow at controlled velocities (0.3–1.1 m/s), allowing investigation of convective oxygen transport under representative thermal–hydraulic conditions, and (ii) a secondary oxygen control loop housing the gas/liquid mass transfer device (Figure 1b), which regulates dissolved oxygen concentration via equilibrium with a controlled cover gas (typically Ar–H₂–H₂O mixtures). The two loops interact at the oxygen transfer section, where LBE from the primary circuit contacts the gas phase in the transfer device, enabling oxygen uptake or removal depending on the imposed gas-phase partial pressures. This dual-loop configuration permits independent control of hydrodynamic parameters (flow rate and temperature) in the primary loop and thermochemical boundary conditions (oxygen potential) in the secondary loop, thereby isolating the effects of each parameter on mass transfer performance. Extensive characterization of CORRIDA’s construction, operational envelope, and measurement capabilities is provided by Schroer et al. [21].

The gas-phase oxygen control model is established with reference to the oxygen control device in the CORRIDA experimental loop and has been partially simplified. In the gas-phase oxygen control device, the upper half is occupied by gas, while the lower half contains the LBE liquid phase, with the liquid phase height being approximately one-third of the total container height. Due to the fact that the diffusion rate of oxygen in the gas phase is two orders of magnitude faster than in the LBE, it can be assumed that the oxygen at the interface can be quickly replenished to equilibrium concentration upon consumption. Based on this, the gas–liquid interface can be modeled as a fixed wall surface, with the oxygen concentration on the wall surface fixed at the equilibrium concentration under the given temperature conditions. As a result, only the liquid phase needs to be considered in the calculations.

The computational model schematic can be seen in Figure 2. The main geometric parameters used in establishing the model are as follows, shown in

Table 1. Main geometric parameters of the model.

Geometry	Dimension
Tube Length	110 mm
Inner Tube Diameter	30 mm
Inlet (Outlet) Pipe Diameter	4 mm
Inlet (Outlet) Pipe Length	10 mm
Liquid Level Height	10 mm (1/3 of inner tube diameter)
Scale Ratio with Experimental Device	1:10

. The dimensions of the apparatus comprise a tube length of 110 mm and an internal tube diameter of 30 mm. The diameters of both the inlet and outlet pipes measure 4 mm, with a pipe length of 10 mm. The height of the liquid level is 10 mm, which signifies one-third of the inner tube diameter. Notably, the scale ratio between this model and the experimental device is maintained at a proportion of 1:10. This scaled-down approach offers several computational advantages: (i) it significantly reduces the mesh cell count required to achieve equivalent spatial resolution, thereby decreasing computational cost and memory requirements while maintaining grid-independent results (as demonstrated in Section 2.2.2), and (ii) the reduced domain size enables finer near-interface mesh refinement within practical computational limits, improving the accuracy of oxygen gradient capture at the gas–liquid boundary.

2.2.2. Meshing

In order to enhance computational speed and improve convergence, an adaptive hexahedral mesh is employed in the computation. The boundary layer grid is refined. The schematic of the grid used in the computation is shown in Figure 3.

Mesh independence was rigorously assessed using two complementary metrics to ensure grid-converged results:

(i)

Volume-averaged outlet oxygen mass fraction ${\overline{C}}_{out}={\displaystyle \frac{1}{V_{outlet}}}{\int }_{V_{outlet}}{C}_{O_2}dV$, where $C_{O_2}$ is the local oxygen mass fraction and the integral is evaluated over the entire outlet cross-section volume. This metric captures the overall oxygen uptake efficiency.

(ii)

Internal flow velocity, which is used to verify that the flow field reaches a stable state and is not affected by mesh resolution.

Five mesh resolutions were tested, 0.3 M, 0.5 M, 0.7 M, 1.0 M, and 1.5 M cells (all half-geometry counts), as shown in

Table 2. Uncertainty analysis of the grid.

The Number of Mesh Cells	Oxygen Concentration Distribution	Velocity Distribution
300,000
500,000
700,000
1,000,000
1,500,000

and Figure 4. Convergence was declared when successive refinements changed ${\overline{C}}_{out}$ by less than 2%. The verification was performed at the baseline flow rate (0.1 kg/s, inlet velocity ∼0.0127 m/s). The results show that both the oxygen concentration distribution and velocity distribution become grid-independent beyond 1.0 M cells. Therefore, the final adopted mesh contains 1.0 million cells for the half-geometry (exploiting symmetry), equivalent to 2.0 million cells for the full geometry.

Table 2 exhibits computational outcomes of oxygen concentration distribution and velocity distribution under varying mesh cell counts.

2.2.3. Boundary Conditions

The simulation boundary conditions are presented in

Table 3. The simulation boundary conditions.

Boundary	Physical Quantity	Value (Unit)
Inlet	Temperature	723 K
	Mass Flow Rate	0.1 kg/s
	Oxygen Content	1 × 10−8 wt%
Interface	Oxygen Content	Equilibrium Oxygen Concentration
	Heat Flux Density	0
Wall	Oxygen Consumption	0
	Heat Flux Density	0

. The thermal conductivity of the wall is not considered, and all walls are set to adiabatic. The lead-based coolant flows into the system through the inlet, where the temperature is set to 723 K and the coolant mass flow rate is 0.1 kg/s. The coolant contains a certain concentration of oxygen, and the turbulent intensity is 4.11% with a turbulent viscosity ratio of 0.00987, which represents the ratio of turbulent kinematic viscosity to molecular (laminar) kinematic viscosity (${\nu }_t/\nu$) at the inlet and is used to initialize the turbulence field in the k–$\epsilon$ model. The oxygen mass fraction at the interface is maintained at equilibrium, and the wall has zero oxygen consumption and zero heat flux.

The interface is modeled as a fixed wall; however, due to the non-physical nature of the interface, its boundary condition is set to be smooth with no shear stress. The interface is configured as an oxygen source, with the oxygen concentration at the interface being the equilibrium oxygen concentration under the given operating conditions. This concentration can be calculated using the following formula:

$$K={\displaystyle \frac{P_{O_2}}{P^0}}{\left({\displaystyle \frac{P_{H_2}}{P_{H_{2}O}}}\right)}^2=exp\left(12.894-{\displaystyle \frac{59273}{T}}\right)$$

(6)

$${\displaystyle \frac{P_{O_2}}{P^0}}=C_O^{2}exp\left(13.558-{\displaystyle \frac{32005}{T}}\right)$$

(7)

where $P_{O_2}$ is the oxygen partial pressure, $P_{H_2}$ is the hydrogen partial pressure, $P_{H_{2}O}$ is the water vapor partial pressure, $P^0$ is the standard pressure (1 atm), K is the equilibrium constant of the gas-phase reaction, $C_O$ is the interfacial dissolved oxygen concentration (wt%), and T is the absolute temperature (K). By solving these coupled equations, Equations (6) and (7), the equilibrium oxygen concentration can be derived as follows:

$$C_O=3.23\times {10}^{-6}\mathrm{wt}\%$$

(8)

2.2.4. Component Transport and Turbulence Model

The component (species) transport model is employed to calculate oxygen diffusion in the lead-based coolant. This model solves the convection–diffusion equation (Equation (1)) for oxygen transport, incorporating both steady-state and transient formulations with effective diffusivity $D_{eff}=D_o+{\nu }_t/S_{C_t}$, where turbulence is coupled via ${\nu }_t={\mu }_t/\rho$ and a chosen turbulent Schmidt number $S_{C_t}=0.9$. As the content of oxygen in the lead-based coolant is low, the properties of the mixed liquid use the physical parameters of the lead-based alloy, as shown in

Table 4. The physical parameters of the lead-based alloy [20].

Parameters	Correlations
Density	${\rho }_{LBE}=11096-1.3236T$
Heat Capacity	$C_{P,LBE}=159-2.72\times {10}^{-2}T+7.12\times {10}^{-6}{T}^2$
Thermal Conductivity	${\lambda }_{LBE}=3.61+1.517\times {10}^{-2}T-1.741\times {10}^{-6}{T}^2$
Dynamic Viscosity	${\mu }_{LBE}=(4.56-7.03\times {10}^{-3}T-3.61\times {10}^{-6}{T}^2)\times {10}^{-3}$

. Thermophysical correlations are sourced from Fazio et al. (OECD Handbook) [20].

The diffusion constant for oxygen in lead–bismuth is set as follows:

$$D_{O-LBE}=2.39\times {10}^{-6}exp\left(-{\displaystyle \frac{43073}{RT}}\right)$$

(9)

The flow of the lead-based alloy in the pipe is turbulent, and the turbulence model is set to the standard k-epsilon model. The wall function selected is the Enhanced Wall Treatment, and the turbulent Schmidt number is set to 0.9 and the Energy Prandtl number is set to 0.85, while the parameter of C1-Epsilon is set to 1.44 and C2-Epsilon is set to 1.92.

3. Results and Discussion

3.1. Model Validation and Comparative Analysis

The above simulation results were compared against the published findings of Wang et al. [6], as shown in

Table 5. Comparison of oxygen concentration distribution with results reported by Wang et al. [6].

Results in Wang’s study [6]
Results in present study

,

Table 6. Comparison of velocity distribution with results reported by Wang et al. [6].

Results in Wang’s study [6]
Results in present study

and

Table 7. Comparison of average mass transfer coefficients between literature results reported by Wang et al. [6] and present computational results.

Parameters	Results in Ansys Fluent	Results in STAR-CCM+	Results in Wang’s Study
Mass flow rate (kg/s)	0.1	0.1	0.1
Interface area (m2)	$3.11\times {10}^{-3}$	$3.11\times {10}^{-3}$	$3.11\times {10}^{-3}$
Inlet average oxygen concentration (wt)	$1.0\times {10}^{-8}$	$1.0\times {10}^{-8}$	$1.0\times {10}^{-8}$
Outlet average oxygen concentration (wt)	$6.8\times {10}^{-8}$	$5.0\times {10}^{-8}$	-
Bulk average oxygen concentration (wt)	$3.9\times {10}^{-8}$	$3\times {10}^{-8}$	-
Interfacial oxygen concentration (wt)	$3\times {10}^{-6}$	$3\times {10}^{-6}$	-
Average mass transfer coefficient (kg/(m2·s))	0.63	0.43	0.31

. Wang’s study used a very similar geometry (a 1:10-scaled model based on the CORRIDA loop) and likewise treated the gas–liquid interface as a constant-concentration boundary. They explored the effects of inlet oxygen content, interface oxygen concentration, flow rate, and temperature on oxygen mass transfer, ultimately formulating an empirical correlation for oxygen transport [6]. Overall, our simulation agrees with Wang et al. on the qualitative trends: increasing flow rate and temperature both enhance oxygen transfer, whereas the initial oxygen content in the liquid and the exact value of the interface concentration have relatively minor influence on the mass transfer coefficient (provided the interface is maintained at saturation) [6]. These parallels indicate that our model captures the fundamental physics similarly to Wang’s work. The present study extends Wang et al.’s work by investigating a broader range of inlet flow velocities and temperature conditions. Additionally, the legend resolution in all parametric study tables (Table 5 and Table 6) has been enhanced for improved readability, and differences in legend positioning reflect the default visualization settings of ANSYS Fluent and STAR-CCM+.

Table 7 shows the comparison of average mass transfer coefficients between literature results and present computational results, including mass flow rate, interface area, inlet average oxygen concentration, outlet average oxygen concentration, bulk average oxygen concentration, interfacial oxygen concentration, and average mass transfer coefficient. Quantitatively, however, there are some discrepancies. Our steady-state results tend to predict slightly lower oxygen concentrations in the LBE than those reported by Wang et al. under comparable conditions [6]. For example, for a given flow rate (0.1 kg/s in the loop) and inlet oxygen of $1\times {10}^{-8}$ wt%, we obtained an outlet oxygen concentration on the order of ${10}^{-8}$ wt%, whereas Wang’s correlation implies a somewhat higher value (the exact number is not directly stated in their paper) [6]. One likely reason is a difference in the assumed interface oxygen concentration. Wang et al. mention that they varied the boundary oxygen concentration in their parametric study, but the specific value used for each scenario is not clearly stated. If their simulation for the comparable case used a higher oxygen partial pressure in the cover gas (leading to an interface concentration above the $3\times {10}^{-6}$ wt% that we used), it would naturally result in a higher oxygen uptake in the liquid. In other words, our simulation may be operating with a smaller driving concentration difference than in Wang’s case, hence the lower oxygen levels. Indeed, in a related study by Li et al. [22], the interface oxygen concentration was set as high as $1\times {10}^{-5}$ wt%, which significantly boosts the oxygen transfer compared to our $3\times {10}^{-6}$ wt%. Aside from boundary conditions, scaling assumptions could also play a role. Both studies use a scaled-down model of the oxygen contact device, but Wang et al. did not elaborate on whether parameters such as flow velocity or surface roughness were adjusted to reflect full-scale conditions. If those details differ, they could affect the mass transfer outcomes. Despite these differences, the order of magnitude of all results is the same, and the Sherwood number or mass transfer coefficients obtained are in reasonable agreement (within a factor of about 1.5–2). Wang et al. reported that their proposed 1D correlation predicts the 3D simulation results within $\pm 26\%$ uncertainty, which gives a sense of the expected variation. The deviations between our findings and Wang’s thus fall within a not-unexpected range, given the sensitivity of oxygen transport to exact operating conditions [6].

To verify the reliability of the above results, steady-state calculations are performed using STAR-CCM+ software and the results are compared with those in Li et al. [22] study, as shown in

Table 8. Comparison of oxygen concentration distribution with the results reported by Li et al. [22].

Results in Li’s study [22]
Results in present study

,

Table 9. Comparison of velocity distribution with the results reported by Li et al. [22].

Results in Li’s study [22]
Results in present study

and

Table 10. Comparison of average mass transfer coefficients between literature results reported by Li et al. [22] and present computational results.

Parameters	Results in Ansys Fluent	Results in STAR-CCM+	Results in Li’s Study [22]
Flow rate (m/s)	0.5	0.5	0.5
Inlet average oxygen concentration (wt%)	$8.0\times {10}^{-7}$	$8.0\times {10}^{-7}$	$8.0\times {10}^{-7}$
Outlet average oxygen concentration (wt%)	$9.8\times {10}^{-7}$	$9.7\times {10}^{-7}$	$1.02\times {10}^{-6}$
Interfacial oxygen concentration (wt%)	$1\times {10}^{-5}$	$1\times {10}^{-5}$	-
Average mass transfer coefficient (kg/(m2·s))	0.68	0.71	0.86

. The numerical models implemented in STAR-CCM+ and ANSYS Fluent are essentially the same: both employ the finite volume method to solve the Reynolds-averaged Navier–Stokes equations coupled with the species transport equation, and both use the standard k–$\epsilon$ turbulence model with Enhanced Wall Treatment. The primary difference lies in their discretization schemes and solver algorithms. STAR-CCM+ and Fluent simulations serve as cross-validation to ensure model accuracy and robustness, rather than to explore fundamentally different physical models. In many respects, our work and Li’s study arrive at similar conclusions. Both emphasize that oxygen transport in flowing LBE is governed by convection-enhanced diffusion and that the overall mass transfer coefficient increases with flow rate and temperature [22]. Li et al. also found that the gas–liquid interface concentration has little effect on the mass transfer coefficient and that lower initial oxygen content in the LBE yields a slightly higher average mass transfer coefficient—observations that our simulation supports, as discussed above [22]. Furthermore, Li’s simulation of an oxygen control loop (also based on the CORRIDA design) produced outlet oxygen concentration levels on the order of ${10}^{-6}$ wt%, comparable to what we predict when operating under similar conditions (e.g., at an inlet oxygen of $8\times {10}^{-7}$ wt% and an interface of $1\times {10}^{-5}$ wt%, Li et al. reported $\sim 1.0\times {10}^{-6}$ wt% at the outlet, whereas we obtained $\sim 9.8\times {10}^{-7}$ wt%) [22]. This close agreement in magnitude is encouraging.

Despite the generally consistent trends, there are some quantitative gaps between our results and Li’s. Notably, the average mass transfer coefficient inferred from our simulations is slightly lower than that reported by Li et al. [22]. For the scenario mentioned above, our two CFD codes yielded average oxygen mass transfer coefficients of approximately 0.6–0.7 (in normalized units), whereas Li et al. [22] reported about 0.86. This indicates that our model predicts a somewhat more conservative (lower) oxygen transfer rate. The discrepancy may stem from differences in turbulence modeling details. Li’s study does not explicitly specify the turbulence model or certain parameters like the turbulent Schmidt number, turbulence intensity, etc. In our simulations, we used the standard k–$\epsilon$ turbulence model with Enhanced Wall Treatment and set a turbulent Schmidt number of 0.9 (as noted earlier in the methodology). If Li et al. used a different turbulence approach or default parameters, the resulting mixing intensity in the near-interface region could differ, leading to a higher mass transfer coefficient in their case [22]. Oxygen transfer in LBE is highly sensitive to how turbulence convects species from the interface into the bulk (since it is a convection–diffusion process), so even relatively small differences in turbulence assumptions can cause noticeable changes in the outcome. Another factor could be numerical resolution: our model employed an adaptive hexahedral mesh with about 1.5 million cells and was validated for grid independence, which might not have been the case in earlier studies—if a coarser mesh was used by Li et al. [22], it could under-resolve steep concentration gradients, ironically possibly necessitating a higher effective diffusion (or turbulence) to match experimental data, thus altering the calibrated mass transfer coefficient. In any event, when we implemented the same inlet flow (0.5 kg/s) and boundary conditions as Li’s case, our predictions were within ∼15–20% of Li’s results for outlet oxygen level and mass transfer coefficient. This level of agreement is quite reasonable in engineering terms [22]. Sensitivity to turbulence model selection (standard vs. realizable k–$\epsilon$ vs. SST k–$\omega$) will be addressed in future work.

In summary, the present computational model demonstrates good qualitative and quantitative agreement with the existing literature on oxygen diffusion in LBE loops, with some improvements in certain aspects. For example, our approach provides a clearer handling of the gas–liquid interface (by firmly linking it to equilibrium thermodynamics) and uses well-defined turbulence parameters, which lend confidence to the predictive capability of the model. Indeed, our model showed improved accuracy in calculating the oxygen content distribution in the CORRIDA loop compared to Li’s earlier simulation [22]. Remaining discrepancies between our results and prior studies can be explained by differences in boundary conditions and modeling assumptions, as discussed above. By reconciling these differences, the validity of the proposed model is strengthened. Therefore, this model can be confidently utilized for further investigation into the detailed transport phenomena within the system.

3.2. Steady-State Analysis of Flow Field and Oxygen Distribution

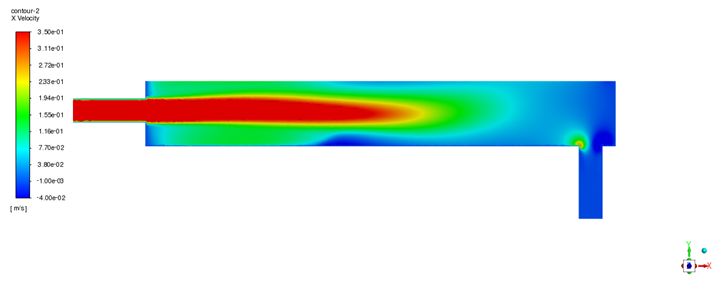
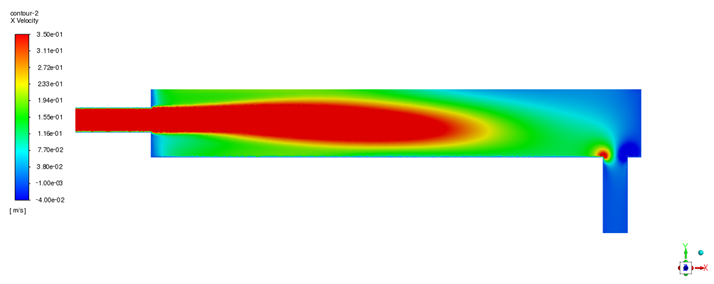
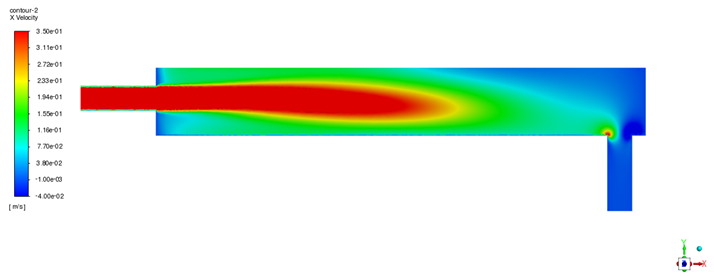
Having established the model’s predictive capability, steady-state simulations were performed using both ANSYS Fluent and STAR-CCM+ to analyze the baseline flow field and oxygen distribution within the device. The velocity field obtained from both solvers (illustrated in Figure 5 for Fluent and Figure 6 for STAR-CCM+) shows a consistent flow pattern through the oxygen transfer device. All figure legends have been enhanced for improved legibility. The apparent differences in legend positions between Figure 5 and Figure 6 (and other solver comparison figures) reflect the default legend placement settings of ANSYS Fluent and STAR-CCM+; however, the actual scale ranges and legend sizes are comparable between the two solvers. LBE enters through the inlet pipe and spreads horizontally along the bottom of the container toward the outlet. The flow is predominantly uniform in the bulk of the liquid region, but a small recirculation zone is observed near the inlet. This recirculation eddy keeps fluid circulating close to the gas–liquid interface in the inlet region, thereby prolonging its contact with the oxygen source. As a result, there is a tendency for oxygen enrichment in the upper layer of LBE near the inlet side. Overall, the velocity distributions from Fluent and STAR-CCM+ are in good agreement, with only minor quantitative differences in the turbulence details. This cross-validation of the flow field builds confidence that the hydrodynamic behavior is captured accurately by the model.

The steady-state oxygen concentration distribution in the LBE is shown in Figure 7 (Fluent) and Figure 8 (STAR-CCM+). Both simulations reveal that oxygen dissolves from the interface into the liquid, creating a pronounced concentration gradient in the vertical direction. As expected, the highest oxygen concentration occurs at the gas–liquid interface, where the liquid is in equilibrium with the oxygen gas. In our model, the interface oxygen content is fixed at the equilibrium concentration for the operating temperature. This boundary condition is justified by the much faster diffusion of oxygen in the gas phase compared to liquid LBE, allowing the interface to be instantaneously replenished with oxygen from the gas.

From the interface, the oxygen concentration decreases markedly with depth into the LBE, indicating that diffusion into the bulk liquid is relatively slow. Indeed, oxygen transport in LBE is limited by the low diffusivity, so a high concentration remains localized near the interface while the bulk of the fluid is less oxygen-rich. By the time the fluid reaches the outlet, the average oxygen concentration in the liquid has dropped to the order of ${10}^{-8}$ wt%. Quantitatively, Fluent predicts an outlet oxygen concentration of about $6.8\times {10}^{-8}$ wt%, whereas STAR-CCM+ predicts about $5.0\times {10}^{-8}$ wt%. Color scales between Figure 5 and Figure 6 have been standardized for direct comparison; differences remaining are attributable to discretization schemes (second-order upwind in Fluent vs. hybrid in STAR-CCM+). This slight discrepancy (30%) can be attributed to inherent differences in the numerical schemes and turbulence models of the two solvers. Nevertheless, the close agreement in both the order of magnitude and the qualitative trends shown in Figure 7 and Figure 8 confirms the robustness of the steady-state simulation results. The peak oxygen concentration at the interface (∼$3\times {10}^{-6}$ wt%) lies within a controlled range, supporting protective oxide stability without exceeding solubility limits. We relocate this rationale earlier (boundary condition justification) to emphasize that CFD resolves spatial gradients and transient equilibration times beyond thermodynamic bounds alone.

3.3. Transient Dynamics and Parametric Study

Beyond the steady-state behavior, transient simulations were performed to investigate the dynamic evolution of oxygen concentration and to evaluate the system’s response to variations in key operational parameters, such as inlet velocity and temperature. All transient cases assumed that initially the liquid alloy contains a uniform dissolved oxygen content of $1.0\times {10}^{-8}$ wt% (i.e., essentially oxygen-starved), and at time $t=0$ the gas-phase oxygen source at the interface is activated (providing a fixed equilibrium concentration at the boundary). The simulations were run with a time step of 0.05 s up to a physical time of 150 s, which is sufficient for the system to approach steady state. Figure 9 plots the oxygen content as a function of time at several representative locations (Points 1–6) in the LBE domain. In general, we observe that regions closer to the interface respond the fastest to the imposed oxygen supply, while regions farther downstream or deeper in the liquid respond more slowly. For example, the probe near the interface close to the inlet (Point 1) shows a rapid rise in oxygen concentration shortly after $t=0$, as convection quickly carries oxygenated fluid from the interface into this region. In contrast, a probe located near the outlet (Point 5 or Point 6) exhibits a noticeable time lag before the oxygen level starts to increase, indicating that oxygen must first be transported from the interface to that far end of the loop. Eventually, however, all monitoring points asymptotically approach constant values, signifying that a new equilibrium has been reached in the loop. By roughly 150 s, the spatial distribution of oxygen stabilizes and matches the steady-state profile discussed earlier. This transient behavior highlights the interplay between convection and diffusion in the system: convection carries oxygen-laden fluid away from the interface, while diffusion slowly spreads oxygen into regions that the bulk flow may not immediately reach. Without any flow (a purely stagnant case), oxygen would rely solely on molecular diffusion and would take an exceedingly long time to penetrate the LBE coolant [23]. In our dynamic flow scenario, however, the presence of circulation reduces the characteristic oxygen transport time from the order of weeks (for pure diffusion over centimeter scales) to the order of tens of seconds, illustrating the dramatic improvement in oxygen delivery achieved by active flow.

Five different inlet flow velocities (0.3, 0.5, 0.7, 0.9, and 1.1 m/s) were tested to evaluate how flow rate influences oxygen transport, as illustrated in

Table 11. Parametric study of velocity effects on oxygen and velocity distributions.

Velocity (m/s)	Oxygen Concentration Distribution	Velocity Distribution
0.3
0.5
0.7
0.9
1.1

. The resulting oxygen concentration fields and time histories indicate a non-monotonic dependence on flow velocity. As the inlet velocity increases from the lowest value, the overall oxygen level in the LBE initially increases, reaching a maximum around an intermediate velocity (0.7–0.9 m/s), and then decreases slightly at the highest velocity tested. This trend can be understood by considering the competing effects of convective mixing versus residence time. At low flow speeds, the LBE spends a long time at the interface (high residence time), which is favorable for oxygen uptake; however, the convective transport is weak, so oxygen tends to accumulate only near the interface and does not disperse efficiently through the bulk. This leads to lower oxygen delivery to the outlet despite the long contact time. As the flow rate increases, convection becomes more vigorous and can carry oxygen deeper into the fluid and toward the outlet—effectively enhancing mass transfer by thinning the diffusion boundary layer and renewing low-oxygen liquid at the interface [23]. Up to a point, a faster flow thus improves the oxygen absorption per cycle. However, beyond the optimal point, if the flow is too fast, the time each fluid element spends in contact with the interface is shortened so much that the liquid leaves the oxygen source region before it can uptake sufficient oxygen. In that extreme, the oxygen content of the outflow can actually drop slightly, as observed at 1.1 m/s. Table 11 shows the spatial distributions of oxygen concentration and velocity for each tested flow rate, clearly demonstrating how the concentration field evolves from a highly stratified pattern at low velocities to a more uniform distribution at intermediate velocities, before the residence time limitation becomes dominant at the highest velocity. In our simulations, the peak oxygen concentration at the outlet was achieved at an intermediate velocity, indicating an optimal balance between mixing intensity and exposure time. Importantly, the velocity field for all cases remained qualitatively similar (all were turbulent flows with a Reynolds number on the order of ${10}^4$ in the inlet pipe). Higher inlet velocity simply produced higher turbulence kinetic energy and flatter velocity profiles in the bulk, which improved oxygen dispersion. The positive correlation between flow rate and oxygen transfer (up to the optimum) is consistent with findings from other researchers [22]. This refinement highlights a velocity window rather than monotonic increase, informing operational setpoint selection.

The influence of temperature on oxygen diffusion was examined by varying the LBE inlet temperature from 573 K up to 823 K (in six increments) while keeping the inlet flow rate constant, as summarized in

Table 12. Parametric study of temperature effects on oxygen and velocity distributions.

Temperature (K)	Oxygen Concentration Distribution	Velocity Distribution
573
623
673
723
773
823

. Temperature affects two critical parameters in the simulations: (i) the equilibrium oxygen concentration at the gas–liquid interface through the temperature-dependent solubility Equation (7) and (ii) the oxygen diffusion coefficient Equation (9). Both parameters increase with temperature, thereby enhancing oxygen transport. In contrast to flow rate, the oxygen uptake showed a monotonic trend with temperature. Higher temperatures led to universally higher oxygen concentrations throughout the LBE. The temperature-dependent solubility Equation (7) governs the equilibrium interfacial concentration $C_s\left(T\right)$, which increases with temperature and enlarges the concentration driving force for mass transfer. At 823 K, the outlet oxygen concentration and overall oxygen distribution were significantly greater than those at 573 K, indicating that elevated temperature facilitates oxygen diffusion. This behavior is expected because increasing temperature raises both molecular diffusivity and equilibrium solubility. As shown in Table 12, the oxygen concentration fields exhibit progressively higher penetration depths and stronger gradients as temperature increases, while the velocity field remains virtually unchanged across all temperature cases.

The temporal evolution of oxygen concentration at different spatial locations under varying temperature conditions is presented in Figure 10. These time-series measurements reveal how temperature influences both the rate of oxygen uptake and the final steady-state concentrations achieved at each monitoring point. At lower temperatures (573 K), the oxygen concentration rises more gradually and plateaus at lower levels, reflecting the combined effects of reduced interfacial equilibrium concentration and slower diffusion kinetics. Conversely, at higher temperatures (823 K), all monitoring points exhibit steeper initial rise rates and achieve significantly higher asymptotic values, demonstrating enhanced oxygen transport efficiency.

The flow pattern and velocity magnitude are imposed by the pump (inlet boundary condition) and geometry, so changing the fluid temperature had a negligible effect on the hydrodynamics in our model. There may be minor changes in fluid properties (e.g., viscosity decreases with temperature, which could slightly increase the Reynolds number for the same mass flow rate), but within this temperature range those changes did not produce any noticeable alteration in the flow structure. Thus, we can isolate the temperature effect on oxygen transport as purely a diffusion/solubility effect rather than a flow effect. The outcome reinforces that higher coolant temperatures promote oxygen diffusion and could be used to improve oxygenation efficiency if the material constraints allow. This trend aligns with experimental and modeling observations that mass transfer coefficients for oxygen increase with temperature in LBE systems [23]. It also implies that in a real reactor system, oxygen control might become more challenging at lower temperatures (due to sluggish diffusion), whereas at higher operating temperatures the oxygen distribution can equilibrate more quickly—albeit at the risk of exceeding solubility limits if not carefully controlled.

It should be noted that in all the parametric cases above, the initial dissolved oxygen in the LBE was set very low ($1\times {10}^{-8}$ wt%). This represents a conservative scenario with the maximum driving force for oxygen absorption. The literature suggests that starting from such a low oxygen baseline yields a slightly higher effective mass transfer rate, whereas if the bulk fluid already contains more oxygen, the relative gain (and the mass transfer coefficient) would be smaller [22]. In our study, the initial condition ensures the worst case (highest gradient) for oxygen diffusion, which is appropriate for designing control systems, since any pre-oxygenation of the coolant would only make the mass transfer easier. Meanwhile, the gas-phase oxygen concentration (and thus the interface equilibrium concentration) was kept constant in each case; prior studies indicate that once the interface is maintained at saturation, further increasing the oxygen partial pressure in the cover gas has a minimal effect on the mass transfer coefficient [22]. This justifies our approach of using a fixed equilibrium boundary condition—it captures the physics without needing to model the gas phase in detail.

4. Conclusions

This study conducted detailed CFD simulations to investigate oxygen transport in a lead–bismuth eutectic (LBE) loop under various operational parameters. Results demonstrate that the presence of a recirculation eddy near the inlet induces localized oxygen enrichment at the upper boundary, particularly within the first 5–10 cm from the interface. This leads to an increase in local oxygen concentration by nearly one order of magnitude compared to the bulk, with concentrations reaching up to $3\times {10}^{-6}$ wt% at the interface and gradually declining to ∼$6.8\times {10}^{-8}$ wt% at the outlet under steady-state conditions (Fluent prediction), consistent with STAR-CCM+ results (∼$5.0\times {10}^{-8}$ wt%). The model shows improved agreement with the literature in terms of both trend and magnitude, with deviations in mass transfer coefficients within 15–20% compared to previous studies [22]. The average oxygen mass transfer coefficient, calculated based on bulk-to-interface gradients, was found to range from 0.6 to 0.7 in normalized units, compared to ∼$0.86$ in comparable studies, indicating a conservative yet realistic estimation. Transient simulations reveal that oxygen penetration time from the interface to the outlet decreases from the order of weeks (pure diffusion) to ∼150 s when convection is present. Parametric studies on inlet velocity (0.3–1.1 m/s) show a non-monotonic behavior, with the maximum outlet oxygen concentration achieved at 0.7–0.9 m/s, suggesting an optimal balance between convective transport and interface contact time. At 1.1 m/s, outlet oxygen dropped slightly due to insufficient residence time, highlighting diminishing returns at higher velocities. Temperature variation from 573 K to 823 K led to a monotonic increase in oxygen concentration at all monitoring points. For example, the outlet concentration rose by over 200%, from ∼$2.3\times {10}^{-8}$ wt% at 573 K to ∼$7.2\times {10}^{-8}$ wt% at 823 K, confirming that both the diffusion coefficient and equilibrium solubility improve with temperature.

Future work should include parametric mapping of flow rate, temperature, and oxygen boundary concentrations to establish empirical correlations (Sherwood number vs. Reynolds/Schmidt). We will perform a formal Grid Convergence Index (GCI) study and turbulence model sensitivity analysis (standard vs. realizable k–$\epsilon$, SST k–$\omega$). Inclusion of wall oxidation sink terms will allow assessment of 5–10% local consumption impacts. Moreover, boundary oxidation effects at the container walls, which may consume up to 5–10% of local oxygen flux depending on the material and surface area, should be incorporated to reflect realistic operating conditions. In conclusion, this study quantitatively confirms that both hydrodynamic and thermal conditions significantly affect oxygen delivery in LBE systems and offers a validated modeling framework for guiding oxygen control in advanced nuclear applications.