Evaporation Behavior of Water in Confined Nanochannels Using Molecular Dynamics Simulation
Abstract
1. Introduction
2. Copper–Water Interaction Forcefield Estimation
2.1. Model Construction
2.2. Forcefields and Interactions
2.3. Simulation Protocol
2.4. Contact Angle Estimation Protocol
2.5. Validation to Experimental WCA:
3. Nanochannel Evaporation Studies
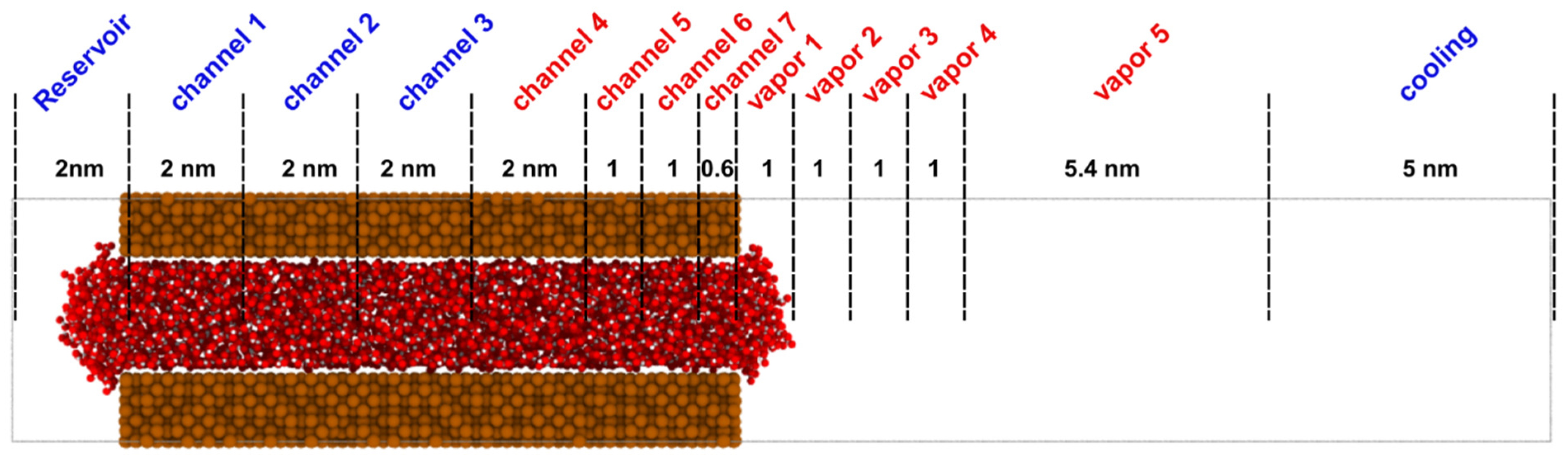
3.1. Materials and Methods for Nanochannel Evaporation
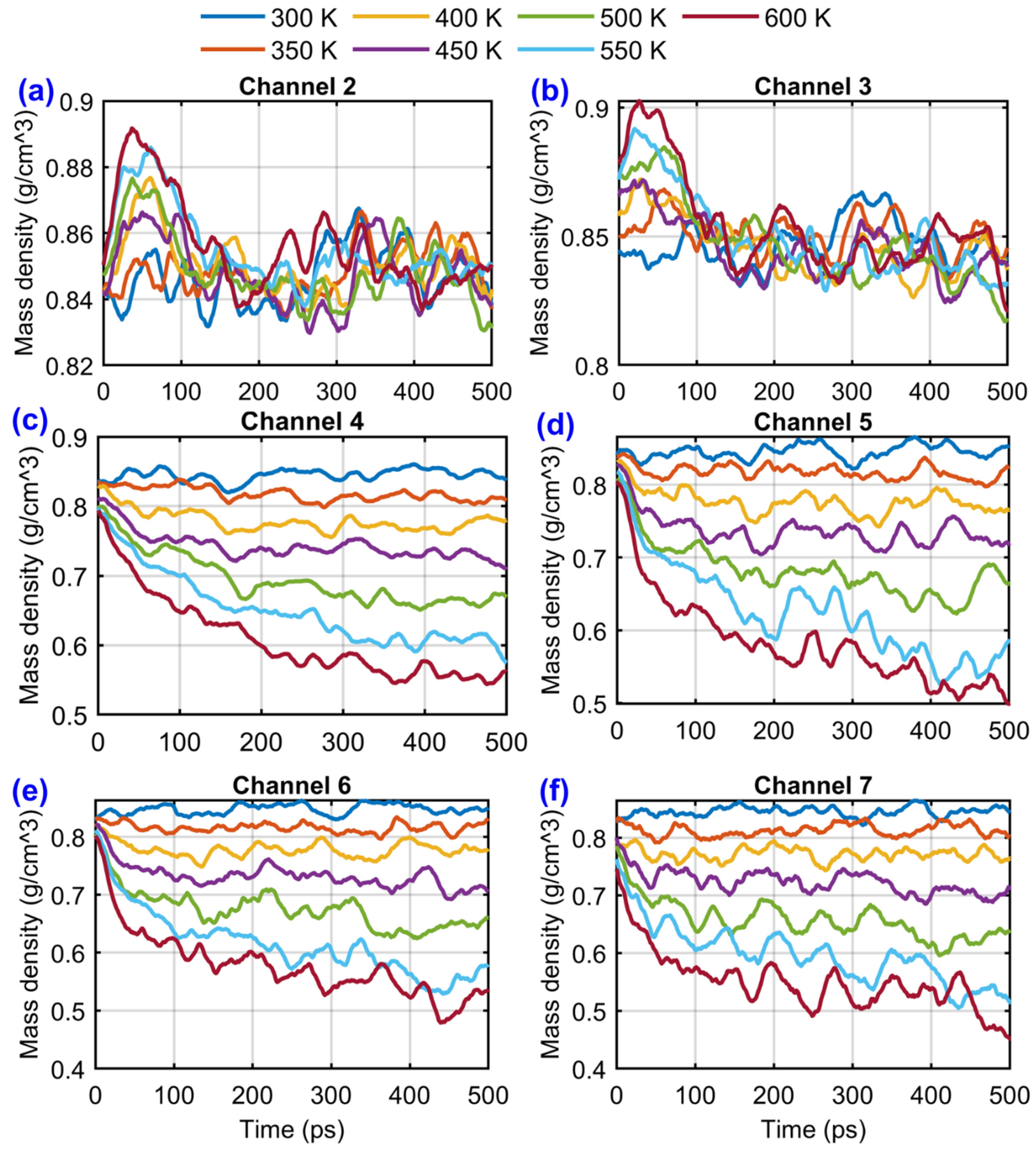
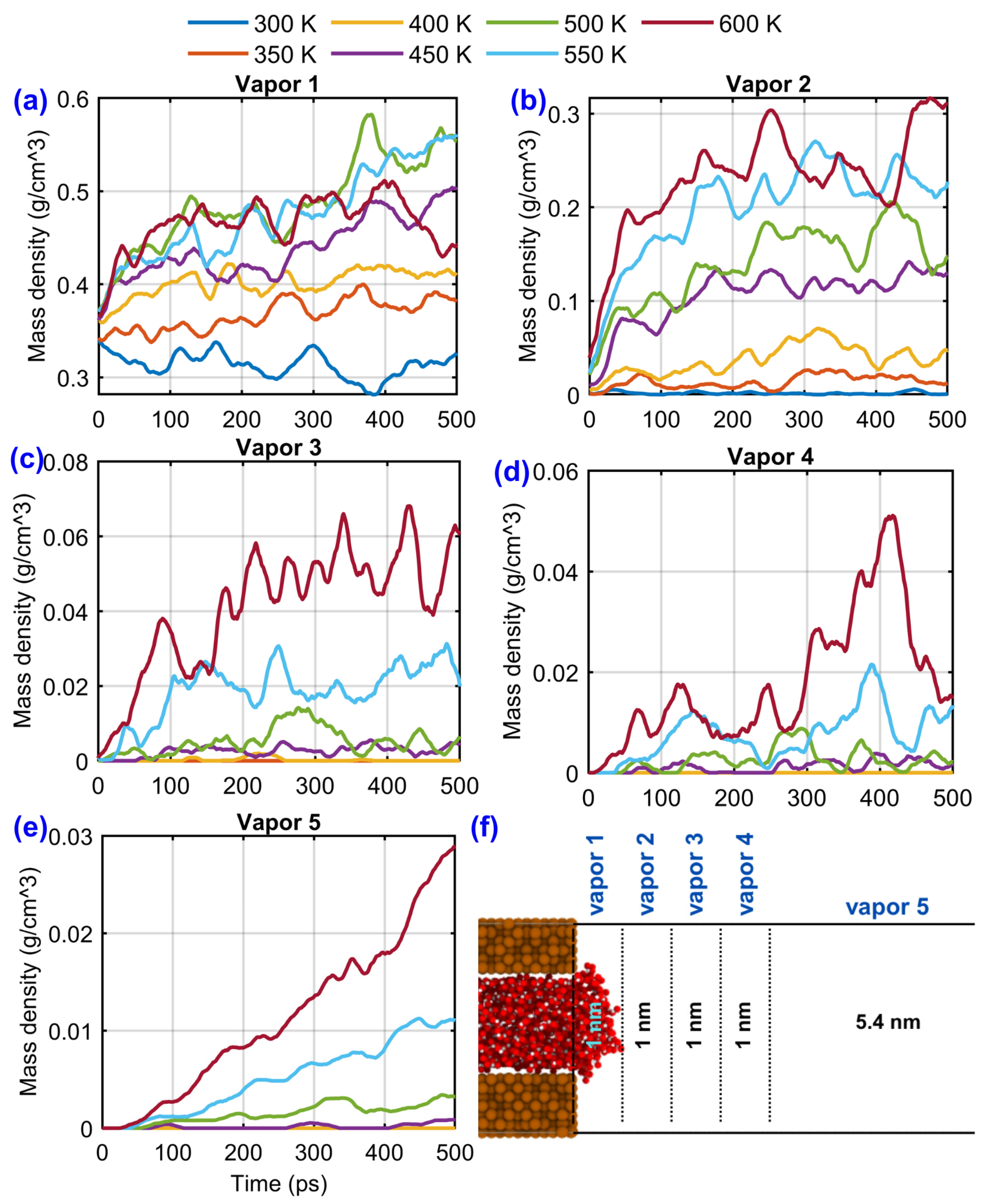
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, Y.; Cai, Y.; Song, L. Condition Assessment of Nuclear Power Plant Equipment Based on Machine Learning Methods: A Review. Nucl. Technol. 2023, 209, 929–962. [Google Scholar] [CrossRef]
- Wang, Y.-J. A Structure-Based Machine Learning Approach for Spatiotemporal Fluctuations in Nuclear Thermal Fluids. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2024. [Google Scholar]
- Song, H.; Liu, X.; Song, M. Comparative Study of Data-Driven and Model-Driven Approaches in Prediction of Nuclear Power Plants Operating Parameters. Appl. Energy 2023, 341, 121077. [Google Scholar] [CrossRef]
- Pavone, A.; Merlo, A.; Kwak, S.; Svensson, J. Machine Learning and Bayesian Inference in Nuclear Fusion Research: An Overview. Plasma Phys. Control. Fusion 2023, 65, 053001. [Google Scholar] [CrossRef]
- Jinia, A.J.; Clarke, S.D.; Moran, J.M.; Pozzi, S.A. Intelligent Radiation: A Review of Machine Learning Applications in Nuclear and Radiological Sciences. Ann. Nucl. Energy 2024, 201, 110444. [Google Scholar] [CrossRef]
- Hong, L.-Z.; Gong, H.-L.; Ji, H.-J.; Lu, J.-L.; Li, H.; Li, Q. Optimizing Near-Carbon-Free Nuclear Energy Systems: Advances in Reactor Operation Digital Twin through Hybrid Machine Learning Algorithms for Parameter Identification and State Estimation. Nucl. Sci. Tech. 2024, 35, 135. [Google Scholar] [CrossRef]
- Gong, H.; Cheng, S.; Chen, Z.; Li, Q. Data-Enabled Physics-Informed Machine Learning for Reduced-Order Modeling Digital Twin: Application to Nuclear Reactor Physics. Nucl. Sci. Eng. 2022, 196, 668–693. [Google Scholar] [CrossRef]
- Boehnlein, A.; Diefenthaler, M.; Sato, N.; Schram, M.; Ziegler, V.; Fanelli, C.; Hjorth-Jensen, M.; Horn, T.; Kuchera, M.P.; Lee, D.; et al. Colloquium: Machine Learning in Nuclear Physics. Rev. Mod. Phys. 2022, 94, 031003. [Google Scholar] [CrossRef]
- Adumene, S.; Islam, R.; Amin, M.T.; Nitonye, S.; Yazdi, M.; Johnson, K.T. Advances in Nuclear Power System Design and Fault-Based Condition Monitoring towards Safety of Nuclear-Powered Ships. Ocean Eng. 2022, 251, 111156. [Google Scholar] [CrossRef]
- Sandhu, H.K.; Bodda, S.S.; Gupta, A. A Future with Machine Learning: Review of Condition Assessment of Structures and Mechanical Systems in Nuclear Facilities. Energies 2023, 16, 2628. [Google Scholar] [CrossRef]
- Qi, S.; Han, B.; Zhu, X.; Yang, B.-W.; Xing, T.; Liu, A.; Liu, S. Machine Learning in Critical Heat Flux Studies in Nuclear Systems: A Detailed Review. Prog. Nucl. Energy 2025, 179, 105535. [Google Scholar] [CrossRef]
- Morgan, D.; Pilania, G.; Couet, A.; Uberuaga, B.P.; Sun, C.; Li, J. Machine Learning in Nuclear Materials Research. Curr. Opin. Solid State Mater. Sci. 2022, 26, 100975. [Google Scholar] [CrossRef]
- Ahmadi, G.; Jahangiri, A.; Ameri, M. The Effects of Transferred Heat and Wall Material on Thermal Behavior of a Nano-Grooved Micro-Heat Pipe, Molecular Dynamics Simulation. Eng. Anal. Bound. Elem. 2024, 160, 1–13. [Google Scholar] [CrossRef]
- Tian, W.; He, S.; Liu, Z.; Liu, W. Experimental Investigation of a Miniature Loop Heat Pipe with Eccentric Evaporator for Cooling Electronics. Appl. Therm. Eng. 2019, 159, 113982. [Google Scholar] [CrossRef]
- Liang, K.; Li, Z.; Chen, M.; Jiang, H. Comparisons between Heat Pipe, Thermoelectric System, and Vapour Compression Refrigeration System for Electronics Cooling. Appl. Therm. Eng. 2019, 146, 260–267. [Google Scholar] [CrossRef]
- Chen, G.; Tang, Y.; Wan, Z.; Zhong, G.; Tang, H.; Zeng, J. Heat Transfer Characteristic of an Ultra-Thin Flat Plate Heat Pipe with Surface-Functional Wicks for Cooling Electronics. Int. Commun. Heat Mass Transf. 2019, 100, 12–19. [Google Scholar] [CrossRef]
- Kong, D.; Kim, Y.; Kang, M.; Song, E.; Hong, Y.; Kim, H.S.; Rah, K.J.; Choi, H.G.; Agonafer, D.; Lee, H. A Holistic Approach to Thermal-Hydraulic Design of 3D Manifold Microchannel Heat Sinks for Energy-Efficient Cooling. Case Stud. Therm. Eng. 2021, 28, 101583. [Google Scholar] [CrossRef]
- Ritz, F.; Peterson, C.E. Multi-Mission Radioisotope Thermoelectric Generator (MMRTG) Program Overview. In Proceedings of the 2004 IEEE Aerospace Conference Proceedings (IEEE Cat. No. 04TH8720), Big Sky, MT, USA, 6–13 March 2004; IEEE: Big Sky, MT, USA, 2004; Volume 5, pp. 2950–2957. [Google Scholar]
- Sun, V.Z.; Sholes, S.; Stack, K.M.; Farley, K.; Del Sesto, T.; Kronyak, R.; Pyrzak, G.; Welch, R.; Lange, R. Evolution of the Mars 2020 Perseverance Rover’s Strategic Planning Process. In Proceedings of the 2024 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2024; IEEE: Big Sky, MT, USA, 2024; pp. 1–16. [Google Scholar]
- Weaver, A.; DeMichael, T.; Woytach, J.; Fleurial, J.-P.; Birch, J.; Davis, S. The next Generation Radioisotope Thermoelectric Generator–Power for Future Deep Space Missions. In Proceedings of the 2023 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; IEEE: Big Sky, MT, USA, 2023; pp. 1–9. [Google Scholar]
- Matthes, C.S.; Woerner, D.F.; Hendricks, T.J.; Fleurial, J.-P.; Oxnevad, K.I.; Barklay, C.D.; Zakrajsek, J.F. Next-Generation Radioisotope Thermoelectric Generator Study. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018; IEEE: Big Sky, MT, USA, 2018; pp. 1–9. [Google Scholar]
- Narayanan, V.; Liburdy, J.; Pence, D. Thermal Applications of Microchannel Flows. Encycl. Aerosp. Eng. 2010, 1–15. [Google Scholar] [CrossRef]
- Stauber, J.M.; Wilson, S.K.; Duffy, B.R.; Sefiane, K. Evaporation of Droplets on Strongly Hydrophobic Substrates. Langmuir 2015, 31, 3653–3660. [Google Scholar] [CrossRef]
- Zhang, J.; Borg, M.K.; Ritos, K.; Reese, J.M. Electrowetting Controls the Deposit Patterns of Evaporated Salt Water Nanodroplets. Langmuir 2016, 32, 1542–1549. [Google Scholar] [CrossRef]
- Plawsky, J.L.; Ojha, M.; Chatterjee, A.; Wayner, P.C. Review of the Effects of Surface Topography, Surface Chemistry, and Fluid Physics on Evaporation at the Contact Line. Chem. Eng. Commun. 2008, 196, 658–696. [Google Scholar] [CrossRef]
- Wang, B.-B.; Wang, X.-D.; Duan, Y.-Y.; Chen, M. Molecular Dynamics Simulation on Evaporation of Water and Aqueous Droplets in the Presence of Electric Field. Int. J. Heat Mass Transf. 2014, 73, 533–541. [Google Scholar] [CrossRef]
- Okuno, Y.; Minagawa, M.; Matsumoto, H.; Tanioka, A. Simulation Study on the Influence of an Electric Field on Water Evaporation. J. Mol. Struct. Theochem 2009, 904, 83–90. [Google Scholar] [CrossRef]
- Yesudasan, S. Thermal Dynamics of Heat Pipes with Sub-Critical Nanopores. arXiv 2024. [Google Scholar] [CrossRef]
- Yd, S.; Maroo, S.C. A New Algorithm for Contact Angle Estimation in Molecular Dynamics Simulations. In Proceedings of the ASME 2015 13th International Conference on Nanochannels, Microchannels, and Minichannels, San Francisco, CA, USA, 6–9 July 2015. [Google Scholar]
- Aboubakri, A.; Yanik, C.; Akkuş, Y.; Koşar, A.; Sadaghiani, A.K. Numerical and Experimental Investigation on Evaporation of Water Droplet on Surfaces With Mixed Wettability. In Proceedings of the ASME 2020 18th International Conference on Nanochannels, Microchannels, and Minichannels Collocated with the ASME 2020 Heat Transfer Summer Conference and the ASME 2020 Fluids Engineering Division Summer Meeting, Virtual, Online, 13–15 July 2020; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2020. [Google Scholar]
- Zheng, R.-H.; Guan, W.-Z.; Zhang, S.-C.; Wei, W.-M. Water at Interfaces Investigated by Neural Network-Based Molecular Dynamics Simulation. J. Phys. Chem. C 2024, 128, 18082–18092. [Google Scholar] [CrossRef]
- Salarnia, M.; Toghraie, D.; Fazilati, M.A.; Mehmandoust, B.; Pirmoradian, M. The Effects of Different Nanoparticles on Physical and Thermal Properties of Water in a Copper Oscillating Heat Pipe via Molecular Dynamics Simulation. J. Taiwan Inst. Chem. Eng. 2023, 143, 104721. [Google Scholar] [CrossRef]
- Loche, P.; Bonthuis, D.J.; Netz, R.R. Molecular Dynamics Simulations of the Evaporation of Hydrated Ions from Aqueous Solution. Commun. Chem. 2022, 5, 55. [Google Scholar] [CrossRef] [PubMed]
- Skarbalius, G.; Džiugys, A.; Misiulis, E.; Navakas, R.; Vilkinis, P.; Šereika, J.; Pedišius, N. Molecular Dynamics Study on Water Flow Behaviour inside Planar Nanochannel Using Different Temperature Control Strategies. Energies 2021, 14, 6843. [Google Scholar] [CrossRef]
- Shahmardi, A.; Tammisola, O.; Chinappi, M.; Brandt, L. Effects of Surface Nanostructure and Wettability on Pool Boiling: A Molecular Dynamics Study. Int. J. Therm. Sci. 2021, 167, 106980. [Google Scholar] [CrossRef]
- Sakamaki, R.; Sum, A.K.; Narumi, T.; Ohmura, R.; Yasuoka, K. Thermodynamic Properties of Methane/Water Interface Predicted by Molecular Dynamics Simulations. J. Chem. Phys. 2011, 134, 144702. [Google Scholar] [CrossRef]
- Abascal, J.L.; Vega, C. A General Purpose Model for the Condensed Phases of Water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Misyura, S.Y.; Andryushchenko, V.A.; Morozov, V.S.; Smovzh, D.V. The Effect of Textured Surface on Graphene Wettability and Droplet Evaporation. J. Mater. Sci. 2022, 57, 1850–1862. [Google Scholar] [CrossRef]
- Lim, E.; Hong, X.; Tan, M.K.; Yu, H.; Wu, H.; Hung, Y.M. Distinctive Evaporation Characteristics of Water and Ethanol on Graphene Nanostructured Surfaces. Int. J. Heat Mass Transf. 2022, 183, 122174. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Y.-B.; Yu, H.; Liu, J.Z.; Easton, C.D.; Wang, Z.; Hu, Y.; Xie, Z.; Wu, H.-A.; Zhang, X.; et al. Ultrafast Water Evaporation through Graphene Membranes with Subnanometer Pores for Desalination. J. Membr. Sci. 2021, 621, 118934. [Google Scholar] [CrossRef]
- Gan, J.S.; Yu, H.; Tan, M.K.; Soh, A.K.; Wu, H.A.; Hung, Y.M. Performance Enhancement of Graphene-Coated Micro Heat Pipes for Light-Emitting Diode Cooling. Int. J. Heat Mass Transf. 2020, 154, 119687. [Google Scholar] [CrossRef]
- Jaikumar, A.; Rishi, A.; Gupta, A.; Kandlikar, S.G. Microscale Morphology Effects of Copper–Graphene Oxide Coatings on Pool Boiling Characteristics. J. Heat Transf. 2017, 139, 111509. [Google Scholar] [CrossRef]
- Wei, N.; Lv, C.; Xu, Z. Wetting of Graphene Oxide: A Molecular Dynamics Study. Langmuir 2014, 30, 3572–3578. [Google Scholar] [CrossRef]
- Pihlajamäki, A.; Matus, M.F.; Malola, S.; Häkkinen, H. GraphBNC: Machine Learning-Aided Prediction of Interactions Between Metal Nanoclusters and Blood Proteins. Adv. Mater. 2024, 36, 2407046. [Google Scholar] [CrossRef]
- Groß, A.; Sakong, S. Ab Initio Simulations of Water/Metal Interfaces. Chem. Rev. 2022, 122, 10746–10776. [Google Scholar] [CrossRef]
- Li, P.; Huang, J.; Hu, Y.; Chen, S. Establishment of the Potential of Zero Charge of Metals in Aqueous Solutions: Different Faces of Water Revealed by Ab Initio Molecular Dynamics Simulations. J. Phys. Chem. C 2021, 125, 3972–3979. [Google Scholar] [CrossRef]
- Carrasco, J.; Hodgson, A.; Michaelides, A. A Molecular Perspective of Water at Metal Interfaces. Nat. Mater. 2012, 11, 667–674. [Google Scholar] [CrossRef]
- Zhu, S.-B. Interactions of Water, Ions, and Atoms with Metal Surfaces. Surf. Sci. 1995, 329, 276–284. [Google Scholar] [CrossRef]
- Zhu, S.-B.; Philpott, M.R. Interaction of Water with Metal Surfaces. J. Chem. Phys. 1994, 100, 6961–6968. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A Tool for Manipulating and Converting Atomic Data Files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Straumanis, M.E.; Yu, L.S. Lattice Parameters, Densities, Expansion Coefficients and Perfection of Structure of Cu and of Cu–In α Phase. Found. Crystallogr. 1969, 25, 676–682. [Google Scholar] [CrossRef]
- Sinha, S.K. Lattice Dynamics of Copper. Phys. Rev. 1966, 143, 422–433. [Google Scholar] [CrossRef]
- Jona, F.; Marcus, P.M. Structural Properties of Copper. Phys. Rev. B 2001, 63, 094113. [Google Scholar] [CrossRef]
- Davis, H.L.; Faulkner, J.S.; Joy, H.W. Calculation of the Band Structure for Copper as a Function of Lattice Spacing. Phys. Rev. 1968, 167, 601–607. [Google Scholar] [CrossRef]
- Davey, W.P. Precision Measurements of the Lattice Constants of Twelve Common Metals. Phys. Rev. 1925, 25, 753–761. [Google Scholar] [CrossRef]
- YD, S.; Maroo, S.C. Origin of Surface-Driven Passive Liquid Flows. Langmuir 2016, 32, 8593–8597. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; In’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D. LAMMPS-a Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Hammonds, K.D.; Ryckaert, J.-P. On the Convergence of the SHAKE Algorithm. Comput. Phys. Commun. 1991, 62, 336–351. [Google Scholar] [CrossRef]
- Andersen, H.C. Rattle: A “Velocity” Version of the Shake Algorithm for Molecular Dynamics Calculations. J. Comput. Phys. 1983, 52, 24–34. [Google Scholar] [CrossRef]
- Lee, B.-J.; Ko, W.-S.; Kim, H.-K.; Kim, E.-H. The Modified Embedded-Atom Method Interatomic Potentials and Recent Progress in Atomistic Simulations. Calphad 2010, 34, 510–522. [Google Scholar] [CrossRef]
- Lee, B.-J.; Baskes, M.I. Second Nearest-Neighbor Modified Embedded-Atom-Method Potential. Phys. Rev. B 2000, 62, 8564–8567. [Google Scholar] [CrossRef]
- Baskes, M.I. Determination of Modified Embedded Atom Method Parameters for Nickel. Mater. Chem. Phys. 1997, 50, 152–158. [Google Scholar] [CrossRef]
- Baskes, M.I. Modified Embedded-Atom Potentials for Cubic Materials and Impurities. Phys. Rev. B 1992, 46, 2727–2742. [Google Scholar] [CrossRef]
- Shi, B.; Dhir, V.K. Molecular Dynamics Simulation of the Contact Angle of Liquids on Solid Surfaces. J. Chem. Phys. 2009, 130, 034705. [Google Scholar] [CrossRef]
- Węglarczyk, S. Kernel Density Estimation and Its Application. In Proceedings of the ITM Web of Conferences, Aviemore, Scotland, 2–3 May 2018; EDP Sciences: Les Ulis, France; Volume 23, p. 00037. [Google Scholar]
- Chen, Y.-C. A Tutorial on Kernel Density Estimation and Recent Advances. Biostat. Epidemiol. 2017, 1, 161–187. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab Software for Spatial Panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef]
- Chen, Y.-C. Molecular Dynamics Study of Phase Change and Interfacial Behavior in Nanoconfined Argon. Master’s Thesis, Southern Methodist University, Dallas, TX, USA, 2025. [Google Scholar]
- Eyupoglu, C. Implementation of Bernsen’s Locally Adaptive Binarization Method for Gray Scale Images. Online J. Sci. Technol. 2017, 7, 68–72. [Google Scholar]
- Chernov, N.; Lesort, C. Least Squares Fitting of Circles. J. Math. Imaging Vis. 2005, 23, 239–252. [Google Scholar] [CrossRef]
- Bickel, P.J.; Doksum, K.A. Mathematical Statistics: Basic Ideas and Selected Topics; Volumes I-II Package; Chapman and Hall/CRC: Boca Raton, FL, USA, 2015. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer Texts in Statistics; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7137-0. [Google Scholar]
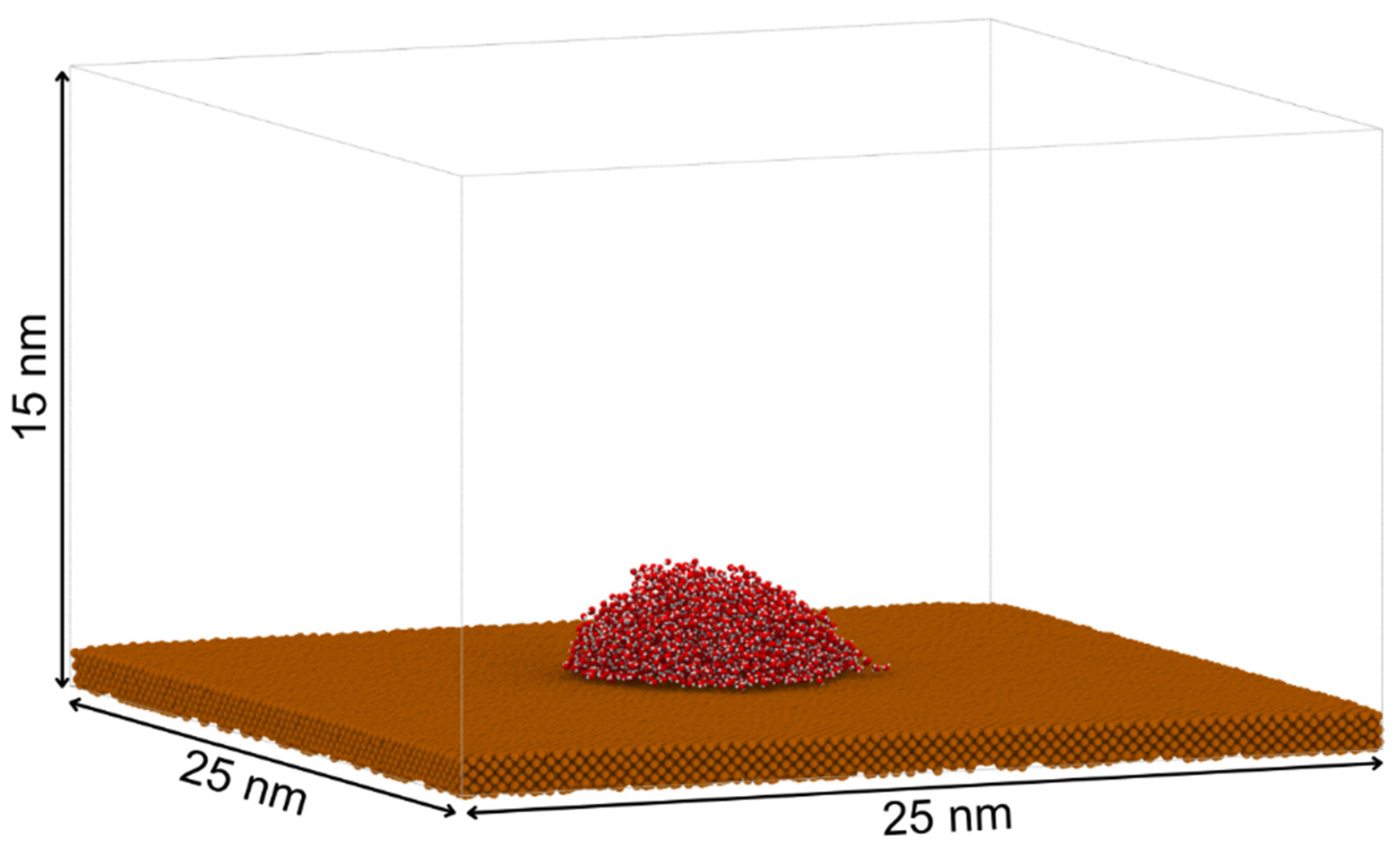
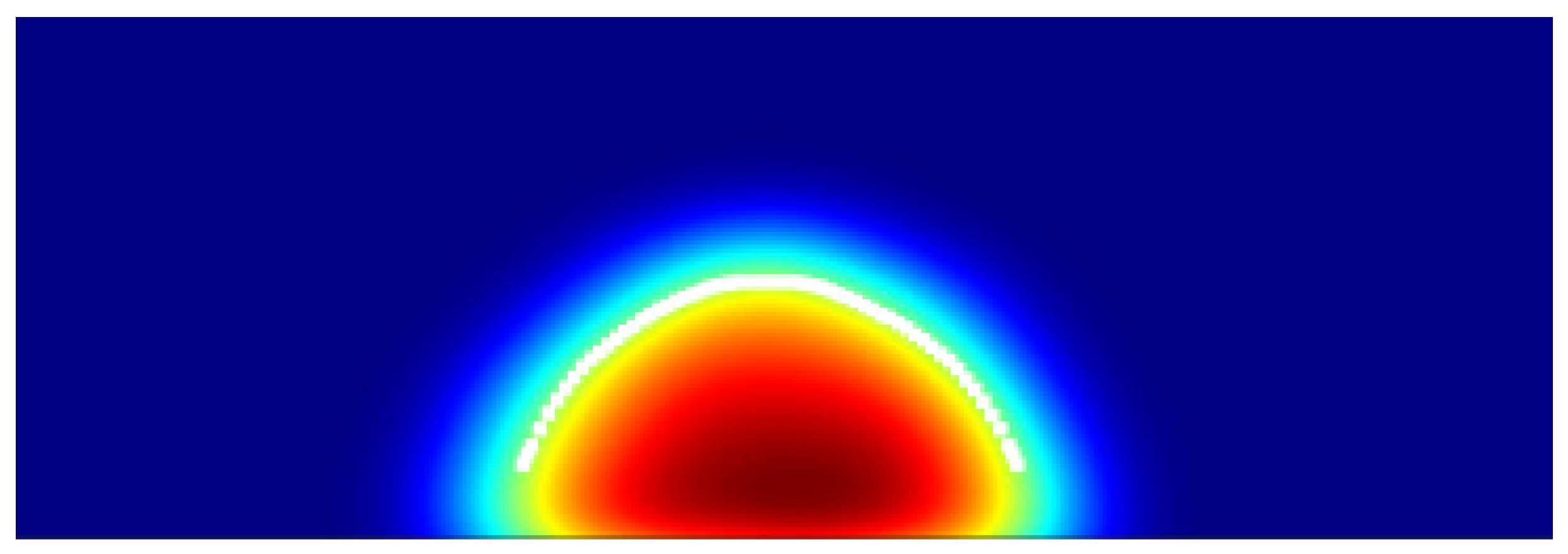

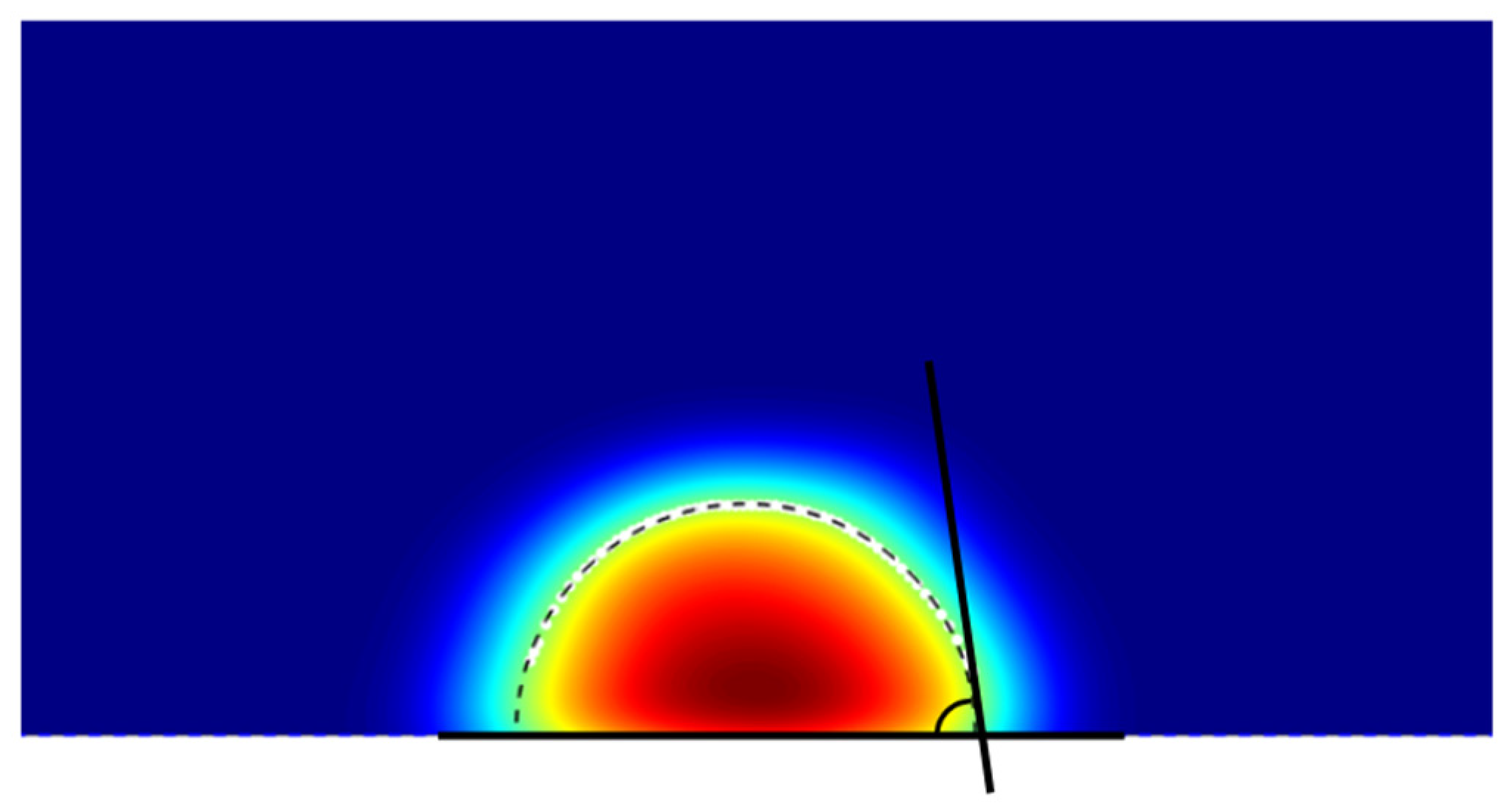

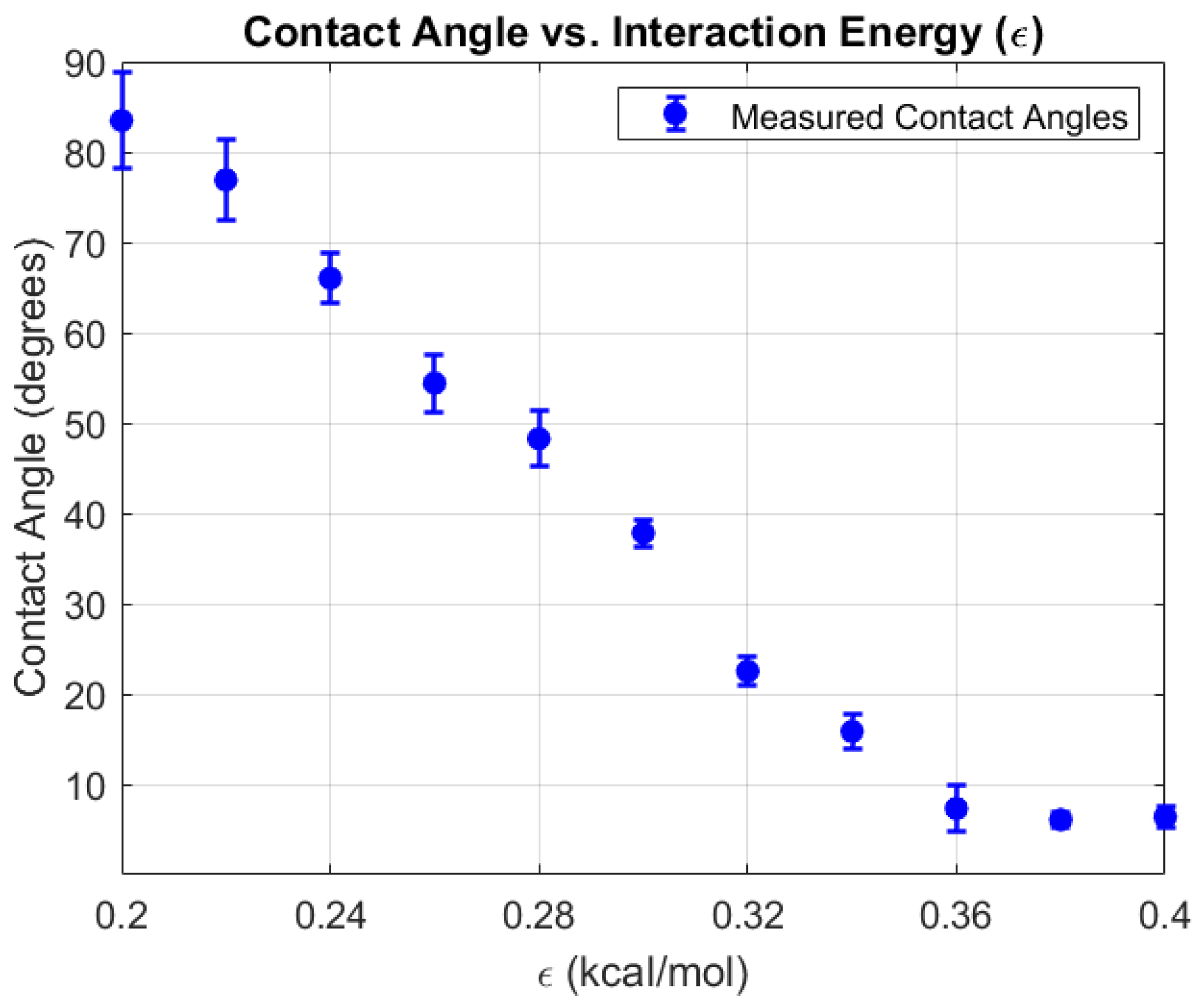


| Eps (kcal/mol) | Contact Angle (°) | Std. Dev. (°) | Experimental WCA (°) |
|---|---|---|---|
| 0.2 | 83.48 | 5.28 | 82.3 |
| 0.22 | 76.91 | 4.51 | |
| 0.24 | 66.01 | 2.72 | |
| 0.26 | 54.42 | 3.2 | 50.2 |
| 0.28 | 48.27 | 3.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yesudasan, S.; Mohammed, M.; Marcello, J.; Taylor, M. Evaporation Behavior of Water in Confined Nanochannels Using Molecular Dynamics Simulation. J. Nucl. Eng. 2025, 6, 43. https://doi.org/10.3390/jne6040043
Yesudasan S, Mohammed M, Marcello J, Taylor M. Evaporation Behavior of Water in Confined Nanochannels Using Molecular Dynamics Simulation. Journal of Nuclear Engineering. 2025; 6(4):43. https://doi.org/10.3390/jne6040043
Chicago/Turabian StyleYesudasan, Sumith, Mamshad Mohammed, Joseph Marcello, and Mark Taylor. 2025. "Evaporation Behavior of Water in Confined Nanochannels Using Molecular Dynamics Simulation" Journal of Nuclear Engineering 6, no. 4: 43. https://doi.org/10.3390/jne6040043
APA StyleYesudasan, S., Mohammed, M., Marcello, J., & Taylor, M. (2025). Evaporation Behavior of Water in Confined Nanochannels Using Molecular Dynamics Simulation. Journal of Nuclear Engineering, 6(4), 43. https://doi.org/10.3390/jne6040043







